典型的车载结构振动疲劳寿命估算方法研究

蔡骏

（中国电子科技集团公司第二十八研究所，江苏 南京 210007）

0 引言

随着车载电子信息系统日益广泛的应用，以及系统运行环境日趋复杂和恶劣，工作中的车辆关键部件的疲劳损伤问题日益突出，运行环境的复杂化导致结构的失效因素随之增多，尤其是车载设备所承受的振动，以及由此产生的振动疲劳破坏严重地影响着结构，甚至全系统的安全性能。目前大量的事故都是由疲劳损伤引起的，由此对车辆的安全可靠性提出了更高的要求，同时也越来越受到研究人员的重视[1]。

在振动疲劳寿命估计方法研究中，Wu[2]对一批7075-T651铝合金进行疲劳试验，对随机载荷下疲劳损伤和疲劳寿命估计方法的适用性进行了验证。疲劳试验结果表明，建立在Palmgren-Miner提出的疲劳损伤估计方法可以通过Morrow的塑性功积累法则来改进。另外，当应力的概率密度函数可以通过零均值的窄带高斯随机过程的瑞利分布来确定时，可以用于窄带随机过程的随机振动理论来进行疲劳寿命估计。针对于随机振动下电子元器件的疲劳失效问题，Steinberg[3]基于高斯分布提出了三区间法。该方法简单、不需要大量的计算，是节省计算时间的有效算法；它建立在大量的实验数据基础之上，用来分析随机振动疲劳失效问题并有着满意的精度。

毛罕平等[4]推导了全面反映加载频率影响的裂纹扩展速率公式，通过数值计算给出了裂纹扩展速率与频率比、阻尼比之间的关系。何泽夏[5]综述了随机振动环境所导致的疲劳损伤及破坏，包括振动疲劳的概念、损伤模型、疲劳裂纹扩展和寿命估算公式，以及振动疲劳试验方法。探讨了宽带随机振动环境下，振动疲劳的理论计算与试验方法。焦群英[6]等分析了共振疲劳与强迫振动疲劳的差异，强调了共振疲劳与结构动态特性的关系，从位移模态推导了应变模态的表达式，讨论了利用应变模态分析的结果来确定共振疲劳危险点的位置的原理。陆榕海和廖振魁[7]针对发动机涡轮叶片的振动及振动疲劳破坏问题进行了理论分析，结果表明叶片的抗振动疲劳的能力主要取决于材料性质及叶片的形式、表面状态，与静强度无关。尚德广和王瑞杰[8-11]提出了一个由固有频率相对变化来描述的疲劳损伤参量，并利用疲劳损伤理论，建立了非线性疲劳损伤演化模型。孙伟、姚卫星和王明珠[12-13]提出了一种结构随机振动疲劳寿命估算样本法。王明珠对结构振动疲劳寿命分析方法进行了研究，并分析了频率对金属材料疲劳寿命的影响，以及阻尼对结构振动疲劳寿命的影响。

综上所述，研究振动环境下结构振动疲劳寿命的分析方法是非常有必要的。目前已有一些振动环境下结构振动疲劳寿命分析方法的研究，但是，在实际的工程中选取哪种方法最为适合尚不明确，所以需要具体问题具体分析。

本文利用有限元软件建立典型的、有缺口的车载结构有限元模型，选择3种常用的振动疲劳寿命判断方法：直接观测法、动态应变法和固有频率法，分析其判断的理论依据和可行性，并开展实验研究。试验分别运用3种判断方法同时监测结构的振动疲劳寿命，讨论研究试验结果，重点分析如何在振动环境下获得最适合的结构寿命判断方法。

1 振动疲劳试验方法

1.1 直接观测法

试件的疲劳破坏监测主要依赖于危险点的裂纹长度监测。根据断裂力学准则，载荷作用下裂纹的尖端会产生应力集中，当应力强度因子达到临界值时，裂纹就会发生失稳扩展，导致结构发生疲劳失效。其临界值为材料断裂韧度KIC，表示结构材料的抗断裂能力。如果应力集中系数用Kmax表示，振动疲劳的失效准则就可以描述为：

直接观测法通过借助显微镜等仪器直接观察结构危险点是否已经产生裂纹，估量裂纹长度，从而判断结构是否已经疲劳破坏，这是试验中最常用的判断方法。

1.2 动态应变法

电阻应变片测量应变的过程为：将应变片粘贴在构件的表面，接入测量电路，随着构件受力，应变片的敏感栅随之变形使其电阻发生变化。电阻与应变的关系如式 （2）所示：

Ks——敏感栅的灵敏系数，它表示导线对所承受的应变量的灵敏程度。

动态应变法，就是根据试件的实际几何外形将合适的应变片粘贴在试件的危险点处，通过动态应变仪监测粘贴处的应变变化，动态应变仪能实时地反映出应变片粘贴处的结构应变，当危险点出现裂纹时，应变必然随之增加，由应变的突然增大并超过限定值可以判断结构已经发生了疲劳破坏。

1.3 固有频率法

通过观察结构的固有频率降低幅度也能有效地判断结构是否发生振动疲劳破坏。频响函数反映了结构的固有特性，疲劳裂纹引发的结构损伤必然会引起频响函数的变化，而固有频率能够及时地体现出频响函数的变化。频响函数为输出信号x（t）与输入信号f（t）两者的傅里叶变化之比，则频响函数FRF（ω）可表示为：

当试验结构内的局部产生裂纹时，结构的强度减弱，从而导致固有频率的降低。固有频率法就是通过观察结构的固有频率降低幅度来判断结构是否发生了疲劳损坏。

2 仿真分析

2.1 仿真方案

振动疲劳试验模型为带缺口悬臂梁，材料为2 mm厚LY12CZ铝合金板材，模型几何形状如图1所示：

图1 试件几何模型 （单位：mm）

试验选取材料的物理属性如表1所示：

表1 LY12CZ铝合金机械性能表

试件左端使用螺栓与底座固定，底座固定在SAI30-H560B16型振动台上。振动台数字控制系统根据给定的激励功率谱控制振动台，使其在一定的范围内振动。

激励的功率谱密度根据GJB 150.16A-2009军用装备实验室环境试验方法，选用高速公路卡车振动环境，以标准中的高速公路卡车振动环境的加速度功率谱密度为基础，在保证疲劳失效机理不发生改变的情况下，选择合适的应力水平进行试验。

对于结构的疲劳失效时间采用多种方法进行确定。1）应变法：在结构危险位置粘贴应变片，当被检测响应点的应变振幅发生异常变化时，认为试件出现裂纹，试验停止；2）固有频率法：采用对结构的固有频率进行实时监控，当结构的第一阶固有频率下降了5%时，认为结构发生疲劳失效；3）直接观测法：采用放大镜实时地观察危险点裂纹的产生，进行失效判定。

试验时，首先，从试验开始计时，每隔10 min通过数字振动控制系统暂停振动台并借用照明工具观察试件缺口处是否有裂纹产生，在观察到动态应变仪显示的应变数值增大到预期破坏应变的2/3时，将间隔时间缩短为2 min。当肉眼能观察到裂纹或者动态应变仪显示应变发生突变时，判断试件在该观测方法下发生疲劳损坏。

采用加速度计测量基础激励的加速度，采用激光测振仪测量试件一点的速度响应，采用动态信号分析仪 （35670A）测量结构的频响函数，每隔5 min测一次频响函数，以监控试件的固有频率变化。当试件的第一阶固有频率下降5%时就可认为试件已疲劳失效。

典型的车载结构损伤加速试验的基本流程如图2所示：

图2 基本流程

数值仿真过程中分别以均方根值为1.59、1.36和1.04 g的功率谱密度信号作为激励的功率谱，谱型如图3所示：

图3 加速度功率谱密度

图 3 中， Y 分别为 0.035、 0.025 和 0.015 g2/Hz。依次以图中的功率谱进行振动测试试验。

2.2 试验结果

按照上述3种判断方法得到试验结束时试件的裂纹情况，如图4所示：

图4 试验结束裂纹的扩展情况

每次激振记录得到的试件寿命如表2所示：

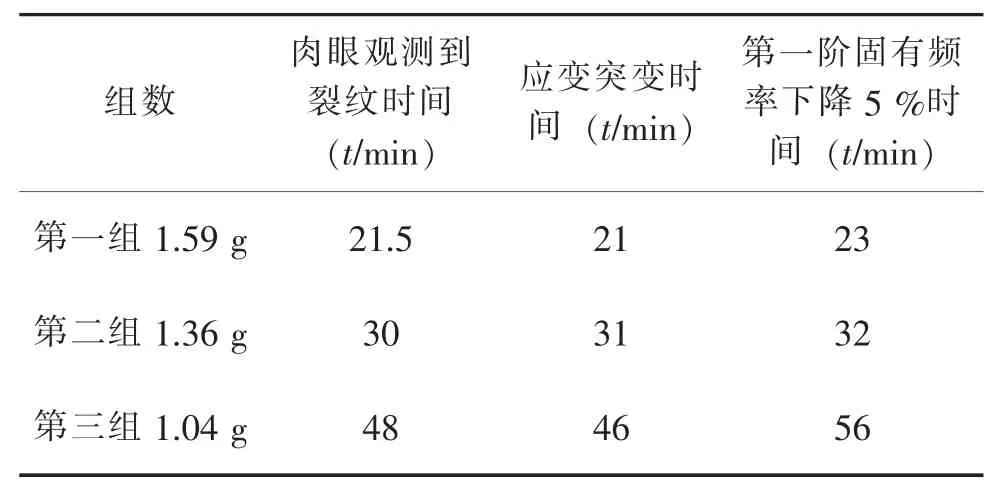
表2 试件疲劳失效时间

图5给出了3种应力水平下的功率谱激振试件得到的第一阶固有频率随时间的变化情况。试件在零时刻固有频率即为未发生破坏损伤时的固有频率，当试件初始的固有频率降低5%时以 “#”标出。如图5（a）所示，随时间的增加，结构的固有频率呈下降趋势，并且随时间的增加，其固有频率减小的速率越来越大，在下降到初始的固有频率5%之后，下降速率将达到最大；比较 （b）、 （c）两图也出现同样的规律。综合比较图5（a）-（c）可知，功率谱的均方根值 （RMS）量级越大，固有频率降低的速度越快，图5（a）中均方根值为1.59 g时，只需23 min固有频率就能下降5%；而为了使固有频率同样下降5%，图5（b）和（c）分别用了32 min和56 min。

图5 不同的应力水平下试件的第一阶固有频率随时间变化图

取第二组实验不同时间所测得的频响函数汇总到图6，反映出频响函数曲线随着时间的推移而产生了明显的变化。图5中，第1～4根曲线分别是零时刻、第15分钟、第25分钟和第32分钟的频响函数曲线，峰值所在的位置随着时间向左有明显的移动，相应的第一阶固有频率也在逐步地降低。这是因为试件刚度对结构动态特性的变化比较敏感，裂纹扩展引起了结构基本参数的变化，从而导致了结构动响应特性的改变。随着时间的推移，固有频率与裂纹的扩展有同步的变化，可以作为判定结构发生振动疲劳的依据。

图6 第二组应力水平下试件不同时刻传递函数图像

3 结论

本文通过实验研究，综合地比较了直接观测法、应变片法和固有频率降低法对结构振动疲劳的判断准确度，以国标规定的裂纹扩展作为振动疲劳破坏判定的参考，探求3种方法各自的优点和适用条件。

a）直接观测法虽被广泛地采用，但是仍存在着一些不易解决的问题。试件在激励下产生振动时，肉眼观测不能准确地反映裂纹的实际情况，因此，所采用的停机观测方法也不能准确地得到裂纹扩展的变化趋势；另外，停机时间的选择也有一定的随机性，停机时观测到的裂纹长度不一定就是结构发生疲劳破坏的临界值。因此，肉眼观测作为一种最终的判断方法，有其实用性，但是，对于需要精确地判断疲劳寿命的实验时，还需要更准确的判断方法。

b）动态应变法方法简单明了，精确度高，对仪器要求不高，适合用于实验室中监测结构的疲劳破坏。但是，应变片粘贴的危险点需要有准确的预判，通过焊接与动态应变仪连接时，在试验过程中，焊点与应变片内部敏感栅有可能受振动影响而产生破坏，从而影响应变仪对结构本身的疲劳破坏的判断。因此，实验结果还需经过对焊点疲劳和应变片本身的结构的检查才能认定是否有效。

c）在频响函数法中，测频响函数所需的传感器和设备较少，频响函数测试准确、方便。采用基础激励的方式，能够有效地避免对结构的特性和边界条件产生影响。利用激光测振仪测量结构的响应，不需与结构直接相连，避免了传感器与结构直接相连引起的结构局部刚度变化。但是，固有频率降低法也有其不足之处。固有频率的降低幅度与裂纹的长度之间的对应关系不够明确，频率的测试精度受到设备和数据采样的限制。

[1]DIRLIK T.Application of computers in fatigue analysis[D].Warwick:Warwick University，1985.

[2]WU W F， LIOU H Y， TSE H C.Estimation of fatigue damage and fatigue life of components under random loading[J].The International Journal of Pressure Vessels&Piping， 1997， 72 （3）： 243-249.

[3]STEINBERG D S.Vibration analysis for electronic equipment[J].3rd Edition.New York： John Wiley&Sons，2000.

[4]毛罕平，陈翠英.考虑动应力时加载频率对裂纹扩展速率的影响 [J].江苏工学院学报，1993，14（6）：26-33.

[5]何泽夏.振动与疲劳 [J].火箭推进，1994（3）：14-20.

[6]焦群英，王书茂，才力，等.用于结构共振疲劳寿命估计的应变模态分析 [J].机械工程学报，1996，32（6）：52-57.

[7]陆榕海，廖振魁.略论发动机涡轮叶片的振动疲劳 [J].洪都科技，1997（1）：19-23.

[8]尚德广.基于动态响应特性的点焊疲劳损伤参量 [J].北京工业大学学报，2004，30（2）：144-147.

[9]WANG Rui-jie， SHANG De-guang， LI Li-sen， et al.Fatigue damage model based on the natural frequency changes for spot-welded joints[J].International Journal of Fatigue， 2008， 30 （6）： 1047-1055.

[10]WANG Rui-jie，SHANG De-guang.Fatigue life prediction based on natural requency changes for spot welds under random loading[J].International Journal of Fatigue 2009， 31 （3）： 361-366.

[11]王瑞杰.基于动态响应分析的点焊接头疲劳损伤与寿命预测 [D].北京：北京工业大学，2008.

[12]王明珠，姚卫星，孙伟 .结构随机振动疲劳寿命估算的样本法 [J].中国机械工程，2008，19（8）：972-975.

[13]王明珠.结构振动疲劳寿命分析方法研究 [D].南京：南京航空航天大学，2009.