混凝土侵彻过程中弹道偏转的影响因素和规律研究*

刘天宋，高旭东，李继政，贾 飞

(南京理工大学机械工程学院，南京 210094)

0 引言

混凝土侵彻问题是武器研制和工程防护的重点问题。虽然弹体侵彻混凝土介质的研究已有很久的历史，但是到目前为止，对于混凝土侵彻问题的研究，大多集中在正侵彻的情况，而对于斜侵彻问题研究较少[1－3]。

斜侵彻现象是普遍存在的。弹体斜侵彻混凝土介质时，弹体的侵彻威力下降，侵彻深度减小，侵彻靶体的弹道会有一定量的偏转，有时甚至会出现弹体在靶板表面跳飞现象。因此，需要研究弹体斜侵彻混凝土时弹道偏转的影响因素和影响规律。

国内外对混凝土侵彻问题的研究主要采用了理论分析法、实验研究和数值模拟法。理论分析主要是根据空腔膨胀理论，并考虑自由表面效应影响来进行侵彻问题的研究。由于斜侵彻实验过程中难以控制弹体的着靶姿态，并且受测试技术的限制，难以获得精确的弹体侵彻过程中运动参数的变化。此外，实验获得的经验公式，往往具有一定的局限性[4]。随着计算机的发展，数值模拟方法的使用在侵彻问题的研究中越来越广泛。近年来还发展出一种基于靶体响应力函数[5－6]来模拟弹体运动和变形的方法。采用此方法进行有限元数值计算可以省略有限元计算中靶体网格的划分，也避免了考虑复杂的接触等问题。

影响混凝土侵彻弹道偏转的因素有很多，文中就刚性弹体斜侵彻半无限厚混凝土靶过程中倾角、入射速度、弹体的质心位置3个因素对弹道偏转的影响规律进行研究。首先，采用半经验公式法，确定了靶体响应力函数，然后利用ABAQUS软件，将靶体响应力函数加载到弹体表面作为有限元计算的边界条件，计算得到了弹体侵彻半无限厚混凝土靶时的弹体质心运动轨迹。通过分析弹体的质心运动轨迹来研究弹体倾角、入射速度和弹体质心位置这几个影响因素对弹道偏转的影响规律。

1 方法原理介绍

1.1 靶体响应力函数

研究表明，弹体在侵彻过程中受到的阻力，可以简化为一个与速度有关的函数，即靶体响应力函数。确定了靶体响应力函数，就不用考虑靶体的响应细节，可直接对弹体侵彻过程进行求解，此即为弹靶分离方法的基本思想。采用弹靶分离思想进行有限元计算不仅省略了靶体网格的划分，而且降低了对计算机硬件的需求，缩短了计算时间。何涛[3]总结了确定靶体响应力函数的方法:经验和半经验公式法、理论分析法和数值模拟法。文中采用Forrestal半经验公式[7]，得到在隧道区弹体表面所受到的压力:

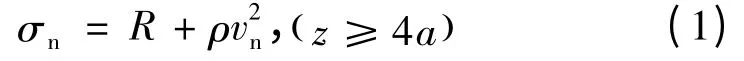
在开坑区，根据何涛[3]等的假设，弹靶接触面上的法向应力为:

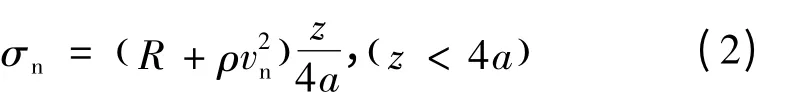
式中:ρ为靶体材料的密度;z为弹体在其竖直方向的位移;a为弹体半径;R为表征弹体表面所受靶体阻力大小的常数;vn为弹体表面上任意点处的法向速度，如图1所示。设弹体表面点P的法向量为n，P点的速度矢量为 v，则 vn=v·n。

图1 弹体表面上任意点的法向速度

1.2 弹体表面摩擦力和自由表面效应的影响

目前对于弹体侵彻混凝土靶过程中的摩擦力计算上没有非常好的模型。式(1)虽然没有显式的包含摩擦阻力项，却能较为准确的预测侵彻深度，这是因为模型中包含了通过侵彻实验确定的隐含摩擦阻力的参数 R[8]。

采用半经验公式法确定的靶体响应力函数是建立在空腔膨胀理论基础上的。弹体斜侵彻半无限大靶体时，弹体表面所受阻力将受到靶体自由表面效应的影响。图2为自由表面效应图。Warren[5]等人给出了受自由表面影响时，空腔表面的径向应力公式:

图2 自由表面效应影响

式中:E为材料杨氏模量;r0为弹体表面上的点到轴线的垂直距离;rs为自由表面到弹体轴线的距离;r1为自由表面到弹体表面的距离，三者之间满足:

其中α、λ和τ是与材料相关的常数，之间满足下式:

式中:σc为混凝土抗压强度。

rp为塑性区边界:

考虑到一旦塑性区边界超过自由表面，由于塑性区内材料的开裂和破碎，整个塑性区将无法继续承载，此时空腔表面的应力会迅速变为零，因此自由表面效应修正函数可以写为:

2 数值计算侵彻深度与经验公式的比较

计算所采用的弹体如图3所示，弹体密度7.8 g/cm3，质量约4.2 kg，假设弹体为刚体。混凝土靶为半无限厚靶，强度48 MPa，无钢筋。利用ABAQUS建立弹体的有限元模型，然后划分网格。

图3 弹体结构图

用式(1)～式(2)确立的靶体响应力函数代替靶体对弹体的作用力，并考虑式(8)中的自由表面效应修正函数，这样在使用有限元方法进行数值模拟时，就可以把靶体的影响用作用于弹体表面单元的压力边界条件来代替。随着侵彻过程中弹体位置和速度的变化，弹体表面所受到的压力也不断改变。显然，当弹体表面某点侵入靶体内部时，该点才受到靶板的作用。弹体斜侵彻还需要考虑弹体和靶的接触分离效应，这里参照 Warren[5]给出的方法，当 vn=v·n的值在某点上为零或为负值时，令为σn零。以上的分析通过编写ABAQUS[9]的用户自定义子程序 VDLOAD实现。由于弹体采用离散刚体，需要指定计算时间步长来求解得到计算结果。

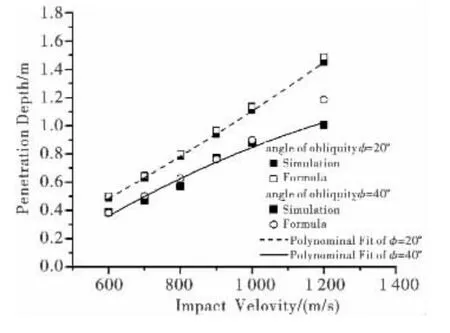
图4 公式计算与仿真计算侵彻深度结果比较

文中将仿真计算得到的侵彻深度与陈小伟[10]的无量纲公式计算结果进行比较。陈的公式假定弹道偏转仅发生在侵彻的开坑阶段，偏转角为δ，此后在隧道区，弹体轴线与靶板法向的夹角为β+δ，弹体以这样的角度姿态沿直线侵彻直到侵彻终止。侵彻的深度为:

式中:X为弹体的侵彻深度;d为弹体直径;N和I分别是撞击函数和弹体几何函数;k为开坑深度系数。

图4给出了弹体分别以20°和40°倾角，不同速度侵彻时，两种方法计算的侵彻深度与结果对比。可见两种方法得到的数据基本吻合，但是当入射速度接近1 200 m/s，入射角度为40°时，结果有较大差距，这是因为此时的入射角度接近跳弹角度，弹道偏转较为严重，经验公式的方法计算误差较大[11]。

3 弹道偏转的影响因素及影响规律分析

3.1 倾角对侵彻弹道的影响分析

本节分析弹体速度为800 m/s时，倾角变化对弹道偏转的影响。图5给出了不同倾角情况下弹体的质心运动轨迹。图6为侵彻深度随倾角变化关系。从图中看出:随着弹体倾角的增大，侵彻深度逐渐减小。侵彻深度随倾角变化关系拟合曲线是上凸的，曲线斜率绝对值逐渐增大，表明倾角对侵彻深度的影响幅度随着倾角的增大呈现增大的趋势。倾角由10°增大为20°时，侵彻深度减小了约5 cm，而倾角由30°增大为40°时，侵彻深度则减小了约15 cm。

图5 速度800 m/s不同倾角侵彻的弹体质心运动轨迹

图7为弹体轴线与竖直方向夹角(偏转角)的变化时程曲线。在初始阶段1，曲线斜率较小，表明侵彻初期偏转变化不大。在阶段2，曲线较陡，表明这段时间弹道偏转较大。在阶段3，弹体基本以恒定的姿势侵彻靶体，直到侵彻结束。图8为整个侵彻过程中弹体偏转角变化与入射倾角关系曲线。可以看出，倾角越大对弹体偏转角的影响越明显。

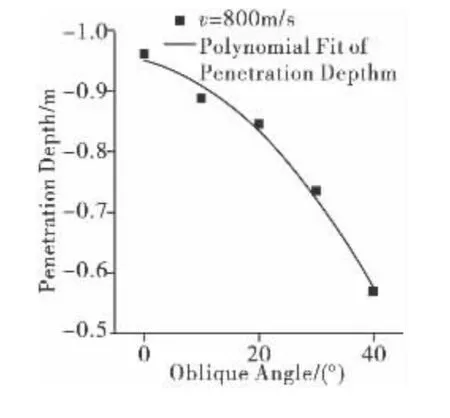
图6 侵彻深度随倾角变化关系

3.2 速度对侵彻弹道的影响分析

本节计算了弹体分别以20°和40°倾角，不同速度侵彻靶板的结果。

图9为弹体偏转角变化与入射速度关系曲线，该曲线呈现下凹状，说明曲线斜率的绝对值是逐渐减小

图7 不同倾角侵彻的弹体偏转角时程变化

图8 弹体偏转角变化与入射倾角关系

的，即入射速度对偏转角的影响幅度随着入射速度的增大呈现减小的趋势，入射速度越大，弹体偏转角越小。

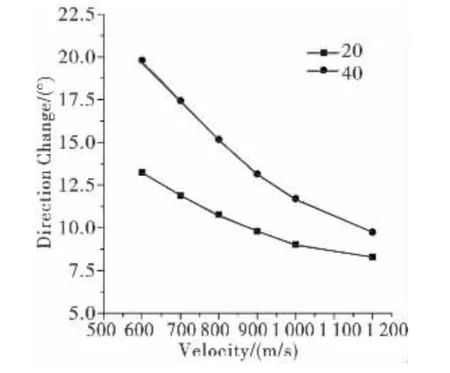
图9 弹体偏转角变化与入射速度关系

3.3 弹体质心位置对侵彻弹道的影响分析

弹体斜侵彻时，弹头受到非对称的载荷作用，使得阻力不通过质心从而使得弹道弯曲。文中在保证弹体质量不变的前提下，通过调整不同位置的密度来调整弹体的质心位置(见图10)。

图10 弹体质心位置

文中计算了弹体以20°倾角，速度900 m/s时不同质心位置的弹体侵彻靶体的质心运动轨迹。图11和图12分别为弹体侵彻深度和偏转角与Lc/L(弹体的质心至弹尖的距离Lc与弹体长度L的比值)变化关系曲线，其中a点所示弹体形心与质心重合时情况。

图11 弹体侵彻深度和与Lc/L关系

图12 弹体偏转角和与Lc/L关系

分析结果表明:相对于形心a来说，Lc/L越大，即质心位置越靠近弹体尾部，弹道偏转越大，侵彻深度越小，且Lc/L对侵彻深度和偏转角度的影响幅度随着Lc/L值的增大呈现增大的趋势。

4 结论

文中采用半经验公式法确定了靶体响应力函数，然后利用ABAQUS软件，将靶体响应力函数加载到弹体表面作为有限元计算的边界条件，得到了刚性弹体侵彻半无限厚素混凝土靶板时的弹体质心运动轨迹。数值计算所得侵彻深度与无量纲经验公式计算结果较吻合。在此基础上研究了刚性弹体斜侵彻半无限厚混凝土时倾角、侵彻速度和弹体质心位置3个影响因素变化对弹道偏转规律的影响，得到如下结论:

1)随着弹体倾角的增大，侵彻深度逐渐减小，弹体偏转角增大，而且倾角对侵彻深度和偏转角的影响幅度随着倾角的增大呈现增大的趋势;

2)入射速度越大，弹体偏转角越小，且入射速度对偏转角的影响幅度随着入射速度的增大呈现减小的趋势;

3)Lc/L越大，即质心位置越靠近弹体尾部，弹道偏转越大，侵彻深度越小，且Lc/L对侵彻深度和偏转角度的影响幅度随着Lc/L值的增大呈现增大的趋势。

对上述规律的认识，对于武器和防护工程的设计有指导意义。文中所采用的靶体响应力函数方法虽然避免了有限元求解中网格划分、接触等问题，但此方法不能准确考虑侵彻中的弹靶分离—接触—再分离情况。另外，文中所有的分析都是通过仿真分析完成的，需要实验研究的进一步验证。

[1]Li Q M，Reid S R，Wen H M，et al.Local impact effects of hard missiles on concrete targets[J]. International Journal of Impact Engineering，2005，32(1/4):224－284.

[2]陈小伟.穿甲/侵彻问题的若干工程研究进展[J].力学进展，2009，39(3):316 －351.

[3]刘勇，宋春明，黄育，等.钢筋混凝土靶体抗弹体斜侵彻试验分析[J].解放军理工大学学报:自然科学版，2013，14(1):64－68.

[4]康海峰.动能弹非正侵彻弹道性能研究[D].南京:南京理工大学，2012.

[5]Warren T L，Hanchak S J，Poormon K L. Penetration of limestone targets by ogive-nosed VAR 4340 steel projectiles at oblique angles:Experiments and simulations[J]. International Journal of Impact Engineering，2004，30(10):1307－1331.

[6]何涛.动能弹在不同材料靶体中的侵彻行为研究[D].合肥:中国科学技术大学，2007.

[7]Forrestal M J，Altman B S，Cargile J D，et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J]. International Journal of Impact Engineering，1994，15(4):395－405.

[8]闪雨，武海军，黄风雷，等.弹体侵彻混凝土侧壁摩擦阻力研究[J].北京理工大学学报，2012，32(1):12 －17.

[9]Systèmes D. Abaqus 6.10:Analysis user's manual[M].Providence，RI:Dassault Systèmes Simulia Corp，2010.

[10]Chen X W，Fan S C，Li Q M.Oblique and normal perforation of concrete targets by a rigid projectile[J]. International Journal of Impact Engineering，2004，30(6):617－637.

[11]马爱娥.弹体非正侵彻(钢筋)混凝土靶数值模拟研究[D].北京:北京理工大学，2007.