粉末注射成形材料微波烧结过程的有限元模拟

石建军，成志强，GELIN J C，柳葆生，BARRIERE T

（1.西南交通大学力学与工程学院，成都610031；2.Femto-ST研究所应用力学实验室，法国贝桑松25000）

0 引 言

微波加热是将材料自身吸收的微波能转化为材料内部分子动能和热能的过程，具有整体加热均匀、升温快速、烧结效率高等优点［1］。在微波加热过程中，电磁波以波的形式渗透到介质内部，引起介电损耗发热，热量从材料内部产生，加之微波的高频振动，使烧结过程中材料内部的温度梯度可以减小到最小程度。同时在微波电磁能作用下，材料内部分子或离子的动能增大，扩散程度增加。这些特性对于提高材料的微观、亚微观均匀性是非常有益的［2］。微波加热还具有选择性加热［3］和无污染性［4］等特点，因此得到了广泛应用。

微波烧结工艺结合了粉末冶金与微波加热技术，近几年被广泛研究。如，晋勇［5］等采用微波烧结新技术研究了纳米金属陶瓷材料的烧结工艺与性能；王美娜等［6］利用微波烧结技术制备了钛酸镁基介电陶瓷；Roy等［7］利用微波技术成功烧结制备了金属粉体，伺候微波烧结技术被广泛应用于制造多种标准金属粉末成形件。作者团队和法国Femto-ST实验室合作，在粉末注射成形和烧结致密化的模拟和试验方面进行了长期研究，并致力于粉末喂料的配方试验［8］，标定PIM（粉末注射成形）过程中的物理参数［9］，建立双向流填充的数学模型［10］并进行传统热烧结试验和数值模拟分析［11］；最近研究团队配置了微波烧结试验设备，对PIM的微波烧结进行进一步理论分析和试验探讨。

微波烧结是一种多物理场的耦合，包括电磁场、热传递和粉末烧结过程的耦合，只有综合考虑这些复杂的耦合现象才能真实地模拟微波烧结过程。现有的研究成果大多集中在对微波加热过程的研究，如，文献［12］运用FDTD方法模拟多模腔的微波烧结试验，文献［13］通过拟和手段分段逼近材料的物理性能，提出了简单的半解析模型，文献［14］建立了一种半解析模型研究微波烧结过程中的能量转换。这些研究耦合了电磁场和热传递的宏观模型，但是都没有涉及材料的致密化过程。鉴于此，作者应用微波加热的相关理论，借助Zhang等［15］提出的热粘塑性本构模型，引入研究团队成员利用热膨胀计和传统热烧结炉标定的适用于多孔体注射成形坯件的宏观烧结模型［16-17］，进一步完善了描述非铁磁性陶瓷粉末成形件微波烧结全过程的数学模型和模拟方法；此外，还借助有限元求解器COMSOL Multiphysics实现了微波电场、热传递和材料致密化过程的耦合计算，展示了单模腔烧结炉微波烧结过程的三维数值模拟结果。

1 微波烧结的数学模型

微波是通过电磁场能量在传播过程中产生损耗的方式对物质进行加热，由于其内部加热的特性，微波损耗作为内热源加热被烧结物体。建立微波烧结过程的数学模型主要需要解决以下五个问题。

1.1 求解Maxwell方程得到加热腔内的电场分布

电磁场问题的宏观控制方程是Maxwell方程。

相对于电场效应而言，微波场中的磁效应对非铁磁性陶瓷粉末成形件的加热作用甚微［18］，故暂不考虑磁效应的影响。加热腔内的电场分布通过式（1）［18］求取。

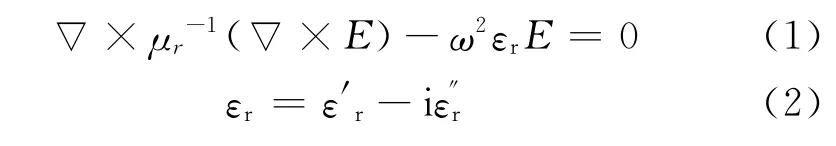
式中：μr为相对磁导率；E为电场强度；ω为微波源的角频率；εr为相对复介电常数（加热腔内的积分区域分为两部分：烧结件占据部分和其它区域，这两个区域具有不同的相对复介电常数）；为介电常数；为介电损耗因子，表征介质的损耗特性，是决定电场分布的重要参数。

在烧结过程中，烧结件内的电磁参数随其密度和温度的变化而变，因此，εr，μr等参数是烧结件密度和温度的函数。这些参数的变化规律，目前尚无标定研究工作，根据文献［19］取参照值进行模拟。

1.2 求解微波烧结过程中热量的分布

材料在电磁场中生成的电阻热即微波加热过程中的损耗功率P，可按式（3）计算［19］。

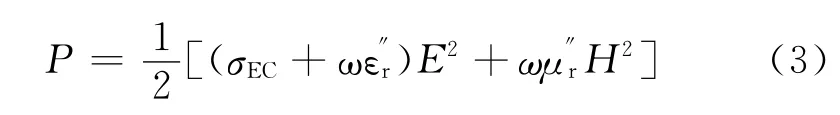
式中：H 为磁场强度；σEC为电导率为被加热物质的磁损耗因子（相对磁导率的虚部）。

由于可以忽略磁效应的作用，故式（3）右端第二项在求解中可被消除。

1.3 求解传热方程得到烧结件内部的温度分布

微波加热的原理是将被加热物体作为微波传输的有耗介质，将有耗介质对微波的损耗变为热能，使加热物体的温度升高。在加热过程中，由于电磁场分布的不均匀性导致损耗功率分布不均匀，继而造成了温度分布的不均匀，所以在微波加热过程中存在着热量的传递过程，可通过求解传热方程（Flourier方程）得到温度场的分布：

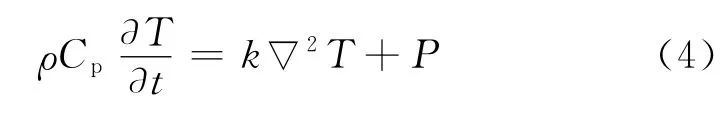
式中：ρ为密度；CP为常压热容；k为热传导系数；T为温度；t为时间。

热力学参数CP和k随烧结过程中烧结件密度和温度的变化而变，需要通过试验测定，模拟中取文献［19］中的参照值。

1.4 求解烧结过程的控制方程得到烧结件的结构响应

PIM材料注射成形及脱脂后的坯件由粉体和孔隙组成，其致密化过程是由高温烧结过程中材料晶粒和晶界的扩散造成的。宏观力学模型基于连续介质力学原理，以类粘塑性本构关系描述粉末的烧结致密化行为，同时考虑材料的弹性效应和热膨胀效应。

烧结过程是一个热力耦合现象，温度场的演变控制烧结件的致密化进程。力学模型的控制方程组包括传统的平衡方程、协调方程，这里不再一一列出，可参照参考文献［20］。烧结过程模拟的特有方程还包括质量守恒方程和烧结本构方程。其中质量守恒方程为：式中为总应变率张量；tr（）为总应变率的迹；为密度变化率；为弹性应变率张量为热应变率张量；为粘塑性应变率张量。

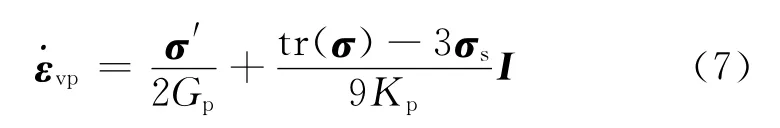
式中：σ为烧结件中分布的应力张量；σ′为应力偏张量；tr（σ）为应力张量的迹；σs为烧结应力；Ⅰ为二阶单位张量；GP和KP分别为烧结过程中多孔体的剪切黏度模量和体积黏度模量。

GP、KP通过试验标定烧结材料的单轴黏度和黏度泊松比确定；烧结应力σs通过不同的烧结温度进程标定；烧结应力张量σ为密度和烧结粉末表面能和界面能的函数，通过热膨胀仪对小试样进行烧结标定［17］。在微波烧结模拟建模的框架下，这些标定参数还是温度进程和密度的函数。

进行模拟还需确定烧结件的热膨胀系数α，以及与弹性变形部分有关的材料参数。这些关系可以示意性地表达为：

α＝α（ρ，T）（8）

Ee＝Ee（ρ，T）（9）

ν＝ν（ρ，T）（10）

式中：Ee为多孔材料的弹性模量；ν为泊松比。

1.5 Maxwell方程、传热方程和材料本构方程的耦合

微波烧结的过程包含三个性质不同的物理过程，其一是微波能在加热腔内的传播过程，在传播过程中由于被烧结材料的损耗，一部分微波能量转化为热能；其二是传热过程，由于加热腔内电场分布的不均匀性，导致被烧结材料内部生热不均匀，存在热传导的过程；其三是材料的烧结致密化过程，PIM材料颗粒在高温状态下会相互连接在一起，颗粒间的空隙逐渐减少或消失，而宏观上则表现为烧结后产品外形收缩，体积减小，密度增大。同时，烧结密度和温度的变化进程也将导致各物理方程的参数变化，形成复杂的耦合关系。

2 微波烧结过程的有限元模拟

2.1 模型定义

微波烧结是微波加热实现烧结致密化的过程。频域电磁分析和分布热源涉及稳态方程的求解；瞬态热传导模拟可获得温度在烧结件内的分布；烧结过程的力学模拟可获得粉末成形件在烧结过程中密度和收缩变形的演化。

PIM材料微波烧结过程的数学模型在时间积分上采用增量算法。在同一时间增量内，分别对代表以上三种现象的控制方程进行分步求解。三种现象的耦合通过时间步的递增实现，在每一时间步内，采用直接法求解该时刻的电场分布，温度场和材料的致密演化需要进行迭代求解。在求解过程中，损耗功率的分布作为内热源引入传热式（4），求解加热腔内的温度分布。将该温度场导入PIM材料的致密化方程和本构方程中，求解得到PIM材料烧结过程的致密演化与变形值。

由于介质的电磁参数和热力学参数随材料密度和温度的变化而变化，在增量求解中可利用更新后的数值求解当前时间步的各变量场。如此循环递增，直到完成预定的烧结过程。所以整个微波烧结过程是Maxwell方程、传热方程和结构平衡方程/材料致密化方程/本构方程的交替数值求解过程，如图1所示。

将微波炉内腔看成是一个金属盒，其与一个2.45GHz、输出功率连续可调的微波源相连。由于忽略微波中的磁效应，故可将微波源设置为一横电（TE）波。炉腔和波导的壁面看成是完美的电导体，用边界条件n×E＝0（n为垂直于边界平面的单位矢量；E为电场强度矢量）表示。利用对称性截取一半模型，由于电场关于对称面镜像对称，所以对称面可看成是完美的磁导体，用边界条件n×H＝0（H为磁场强度矢量）表示。烧结模拟过程中要考虑重力效应。

模拟使用的陶瓷粉末成形件的物理参数取自参考文献［19］中氧化锆粉体的近似参数。微波源输入功率设为恒定值1kW，初始温度T0＝293K，初始相对密度ρr0＝0.65。烧结材料的复介电常数εr＝10-i0.1e0.0017（T-293），磁导率k＝1，密度 ρ＝600 0ρrkg·m-3（ρr为相对密度），热传导率k＝30ρrW·（m·K-1），热容CP＝900ρrJ·kg-1·K-1，热膨胀系数α＝1.2×10-2K-1，重力系数g＝9.8N·kg-1，体积黏度模量GP＝1×1011Pa，剪切黏度模量KP＝1×1011Pa，泊松比ν＝0.33。需要强调的是，由于试验测试技术的局限性，类似于材料的相对复介电常数、电导率等电介质参数以及控制材料致密化过程的热粘弹塑性本构关系，目前仍是材料科学领域需要研究的课题，从文献查阅的相关数据也存在很大差异。因此，上述部分参数设置为初始参数，在目前的数值算法研究中暂时作为常量处理。为了准确真实地模拟微波烧结过程，提供真实的材料参数是至关重要的。而作者侧重于微波烧结致密化过程数值模拟方法的研究，在下一步的研究工作中将通过试验手段获得符合微波烧结过程的尽可能真实的材料参数。

图1 微波烧结过程模拟多物理场耦合的示意Fig.1 Abridged general view of coupling of multi-physics in simulation of microwave sintering

2.2 数值计算

对PIM材料微波烧结过程的数值模拟，需要联合求解上述建立的数学模型中涉及的五个问题。这里借助有限元软件COMSOL Multiphysics作为求解器，使用该软件自带的4个计算模块：利用射频模块中的电磁波（“rfw”）求解电磁场的分布；利用广义热传递模块的瞬态分析（“htgh”）求解温度场分布；利用结构力学模块中的实体、应力-应变分析（“smsld”）求解烧结件的结构响应；利用通用形式偏微分方程（PDE模式）的瞬态分析（“g”）求解质量守恒方程（5），更新瞬时密度衍变值。

为确定放置粉末成形件的适当位置，首先对微波烧结炉的空炉腔做电磁场分布分析，如图2所示。由图2可知，为了让粉末成形件尽可能多地吸收电磁波的能量，应该将其置于电场峰值附近的区域，如图3所示。这里采用形状规则的长方体，可直接使用COMSOL软件自带的四面体自由网格划分模型，通过调节网格尺寸参数，可控制不同区域的网格大小。烧结区域的有限元模型如图4所示。为了简化模型，假设粉末成形件外表面与烧结炉内腔环境热绝缘。在进行热传递、结构应力-应变和相对密度演化的求解时，抑制微波炉内炉腔部分的计算，而只计算粉末成形件内部材料的反应。

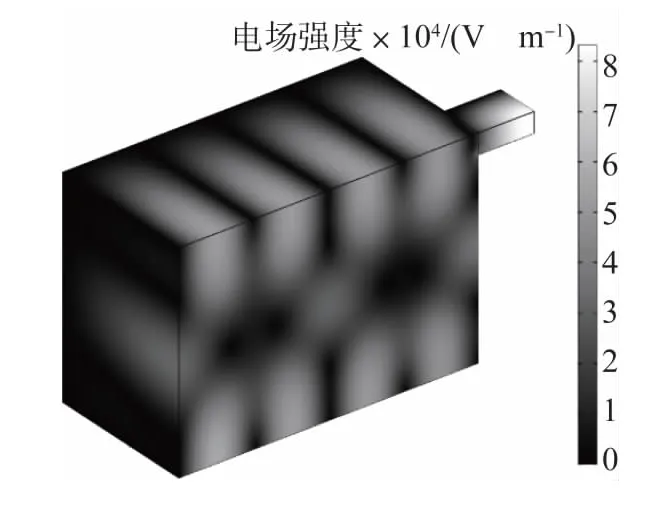
图2 微波烧结炉空炉腔内的电场分布Fig.2 Electric field in empty cavity of microwave sintering furnace

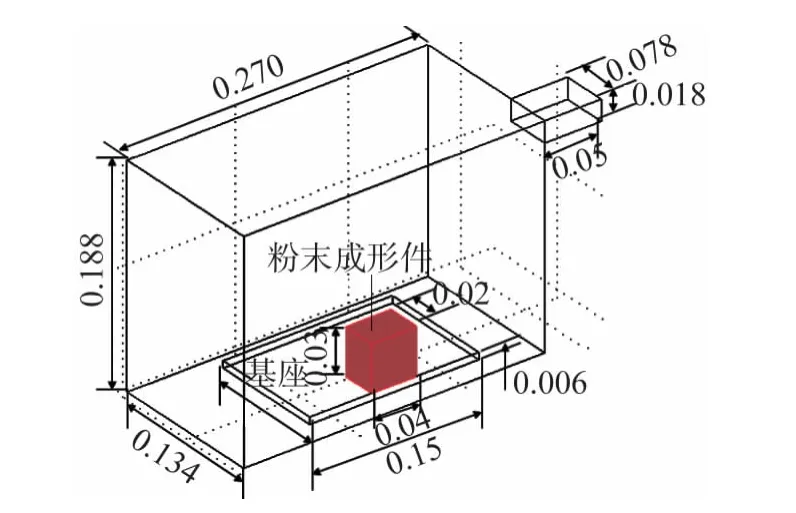
图3 粉末成形件放置的位置Fig.3 Placement of powder molding sample

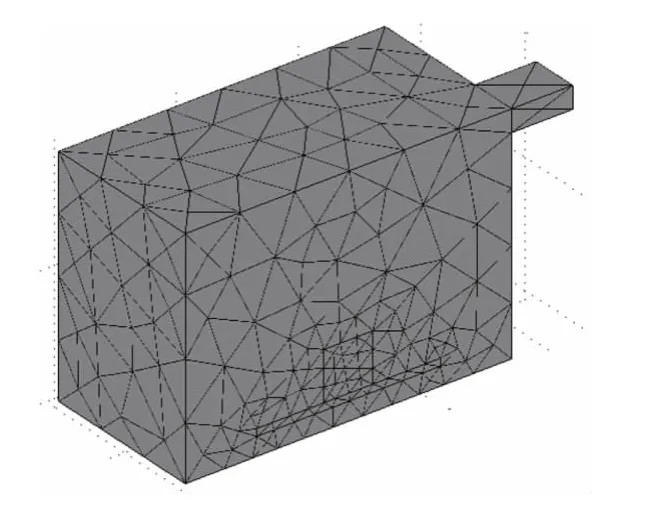
图4 COMSOL中的有限元模型Fig.4 FEM in COMSOL

从图5中可以看到，经过1 500s之后，PIM烧结件内部温度达到1 650K左右，峰值温度位于烧结件内部，且其整体温度梯度不大。从图6，7中可以看到，由于热效应和重力效应的共同作用，此时，PIM烧结件向中心和底部方向产生了比较明显的收缩变形，这就是烧结的致密化现象。

图5 加热1 500s后PIM烧结件内部温度场的纵向截面云图Fig.5 Longitudinal section of temperature field inside PIM sintered sample after heating for 1 500s

图6 加热1 500s后PIM烧结件x方向的线位移云图Fig.6 Displacement along x-direction of PIM sintered sample after heating for 1 500s

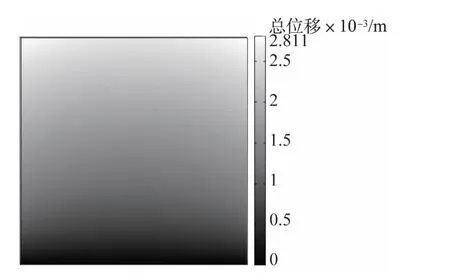
图7 加热1 500s后PIM烧结件的总位移云图Fig.7 Total displacement of PIM sintered sample after heating for 1 500s

采用COMSOL非线性求解器进行求解，整个微波烧结过程耗时1 500s（25min），从0～1 500s均等截取6个时间值作为计数点保存对应时刻的结果。从图8，9可以看到，由于复介电常数是温度的函数，其损耗因子随温度的升高而增大，故在加热的初始阶段，PIM材料内部产生的电阻热很小，加热缓慢；在600s之前，材料内部的温度和材料的相对密度无明显变化，600s之后，PIM材料内部温度持续急剧升高并达到峰值，其相对密度也随着温度的升高而不断增加，最后接近完全致密材料。由于模拟采用固定的输入功率（1kW），所以材料内部温度会不断升高，如此时调整微波源输入功率，即可控制微波烧结进入保温阶段，随后进行冷却处理。将模拟结果与Charmond等［21］对纳米级氧化锆粉末成形件微波烧结的试验结果进行对比分析。Charmond等［21］发现氧化锆粉体在加热温度低于400℃时与微波的耦合作用较微弱，当温度超过400℃时，微波的加热效应逐步增强，这与模拟结果（图8，9）十分吻合。由图10可见，有限元模拟结果比微波烧结的试验结果略小，这是因为采用的烧结模型并非经过标定的确切本构关系，所以得到的相对密度及其变化趋势只具有参照意义。

图8 粉末成形件中心产生的电阻热-时间曲线Fig.8 Evolution of resistance heat generation in the center of PIM sample

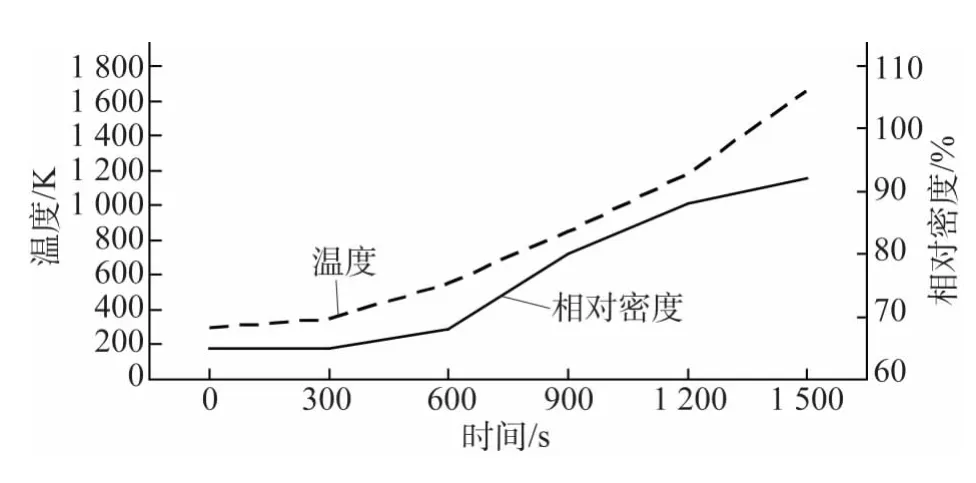
图9 PIM烧结件中心温度和相对密度的变化曲线Fig.9 Variation curves of center temperature and relative density of PIM sintered sample

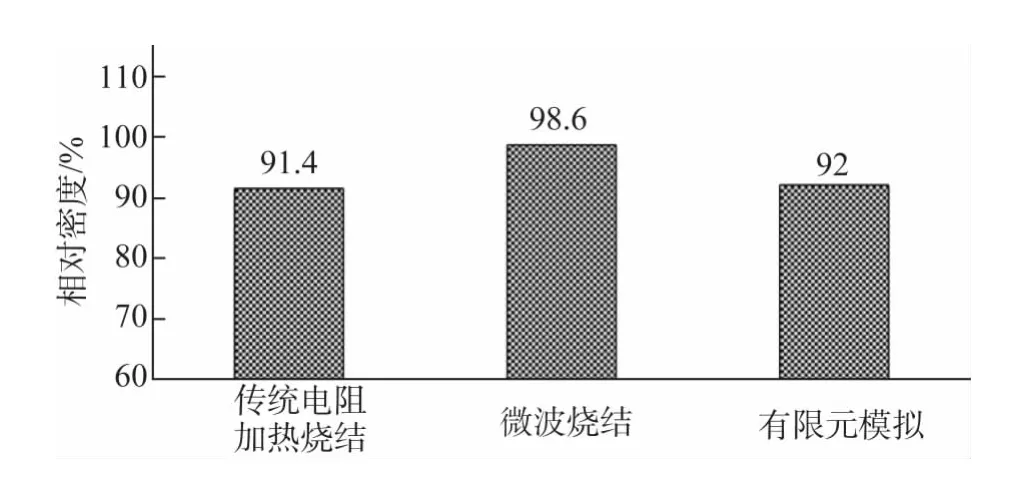
图10 在1 360℃下采用不同方法制得烧结件相对密度与有限元模拟结果的比较Fig.10 Comparison of relative density of sintered samples prepared at 1 360 ℃ by different sintering processes with FEM result

3 结 论

（1）利用COMSOL Multi-physics有限元软件模拟氧化锆粉末成形件的微波烧结过程，模拟结果表明整个微波烧结过程耗时1 500s，初始阶段由于粉末成形件内部温度较低，粉体材料吸波能力较弱，加热缓慢；当温度升至400℃后，粉末成形件内部温度持续急剧升高；当加热至1 360℃时，烧结件的相对密度达到92%，满足粉末烧结工艺要求。

（2）建立的数学模型和有限元手段能有效模拟微波烧结过程中PIM材料内部的电场、温度场分布以及密度的衍化过程，为深入分析和认知微波烧结过程提供了有效工具。

（3）为了更准确模拟微波烧结过程，需要通过试验手段标定粉末材料真实的物理参数与本构关系，同时应具体考虑边界条件、重力以及摩擦力等外部影响的因素。

［1］陈鼎，李林，陈振华.金属材料微波烧结的研究现状［J］.机械工程材料，2012，36（4）：7-10.

［2］GUO Y，YI J，LUO S，et al.Fabrication of W-Cu composition by microwave infiltration［J］.Journal of Alloys and Compounds，2010，492：L75-L78.

［3］SHON I J，KIM B R.Initial stage sintering of binderless tungsten carbide powder under microwave radiation［J］.Ceramics International，2011，37（2）：505-512

［4］TOMPSETT G A，CONNER W C，YNGVESSON K S.Microwave synthesis of nanoporous materials［J］.Chemphyschem，2006，7（2）：296-319.

［5］晋勇，薛屺，汤小文，等.纳米金属陶瓷材料的微波烧结工艺研究［J］.机械工程材料，2004，28（12）：49-51.

［6］王美娜，丘泰，沈春英.钛酸镁基介电陶瓷的微波烧结［J］.机械工程材料，2009，33（1）：23-25.

［7］ROY R，AGRAWAL D，CHENG J，et al.Full sintering of powdered-metal bodies in a microwave field［J］.Nature，1999，399：668-670.

［8］KONG X，QUINARD C，BARRIERE T，et al.Mixing and characterisation of stainless steel 316Lfeedstock［J］.International Journal of Material Forming，2009，2（1）：709-712.

［9］QUINARD C，BARRIERE T，GELIN J C.Development and property identification of 316Lstainless steel feedstock for PIM andμPIM［J］.Powder Technology，2009，190（1/2）：123-128.

［10］LARSEN G，CHENG Z Q，BARRIERE T，et al.Modeling and numerical simulation of biphasic fluid flow［J］.Steel Research International，2010，81（9）：1458-1461.

［11］SONG J，BARRIERE T，LIU B，et al.Experimental and numerical analysis on the sintering behaviours of injection moulded components in 316Lstainless steel powder［J］.Powder Metallurgy，2010，53（4）：295-304.

［12］ISKANDER M D，ANDRADE A O N M.FDTD simulation of microwave sintering of ceramics in multimode cavities［J］.IEEE Trans Microwave Theory and Techniques，1994，42（5）：793-799.

［13］KOZLOV P V，RAFATOV I R，KULUMBAEV E B，et al.On modeling of microwave heating of a ceramic material［J］.Journal of Physics D：Applied Physics，2007，40（9）：2927-2935.

［14］LASRI J，RAMESH P D，SCHACHTER L.Energy conversion during microwave sintering of a multiphase ceramic surrounded by a susceptor［J］.Journal of American Ceramic Society，2000，83（6）：1465-1468.

［15］ZHANG B，GASIK M.Stress evolution in graded materials during densification by sintering processes［J］.Computational Materials Science，2002，25（1/2）：264-271.

［16］QUINARD C，SONG J，BARRIERE T，et al.Elaboration of PIM feedstocks with 316Lfine stainless steel powders for the processing of micro-components［J］.Powder Technology，2011，208（2）：383-389.

［17］SONG J，BARRIERE T，GELIN J C，et al.Powder injection molding of metallic and ceramic hip implants［J］.International Journal of Powder Metallurgy，2009，45（3）：25-34.

［18］SANTOS T，VALENTE M A，MONTERIO J，et al.Electromagnetic and thermal history during microwave heating［J］.Applied Thermal Engineering，2011，31（16）：3255-3261.

［19］BOUVARD D，CHARMOND S，CARRY C P.Mutiphysics simulation of microwave sintering in a monomode cavity［C］//12th Seminar Computer Modeling in Microwave Engineering＆ Applications.Grenoble，France：［s.n］，2010.

［20］GERMAN R M.Sintering theory and practice［M］.［S.l.］：Wiley-Interscience Publication，1996.

［21］CHARMOND S，CARRY C P，BOUVARD D.Densification and microstructure evolution of Y-tetragonal zirconia polycrystal powder during direct and hybrid microwave sintering in a single-mode cavity［J］.Journal of the European Ceramic Society，2010，30（6）：1211-1221.