旋转式惯导系统误差传播特性
乔 猛,尹洪亮,方向红,张 滨
(1.中国人民解放军92337 部队,辽宁 大连116023;2.中国舰船研究院,北京100192;3.中国船舶工业系统工程研究院,北京100036)
0 引 言
众所周知,捷联惯导系统的误差来源包括惯性元件输出误差(零偏误差、标度因数误差、安装误差和随机误差等)、原理性误差(圆锥误差、划船误差、涡卷误差)和计算截断误差,这些误差在导航解算过程中传播,会不同程度影响导航精度。其中,惯性元件输出误差是惯导系统的主要误差源,采用旋转调制技术可以对惯性元件输出误差进行有效补偿,在惯性元件本身的输出精度没有改善的情况下提高系统的导航精度[1-5]。
并非所有的器件误差均能够通过旋转被调制平均掉,研究旋转式惯导系统误差传播特性有助于系统的设计[6],例如,合理的双轴转位方案能够最大程度地调制掉器件误差,从而使系统精度达到最优,而设计一个好的双轴转位方案必须充分了解旋转式惯导系统的误差特性[7-8]。本文将研究旋转式惯导系统误差传播形式,并与传统的捷联式惯导系统进行对比,以便从原理上理解这两类系统的差别。进一步分析对惯导系统影响最大的常值误差经调制后的形势,仿真验证其调制效果。
1 单通道误差分析
在惯导系统的误差传播方程中,等效北向和等效垂向陀螺漂移会造成解算经度误差随时间而发散,因此将陀螺漂移对系统经度误差的影响单独列出进行考察。忽略交叉耦合项,静态下单通道误差模型为:

式中:φE,φN和φU为3个姿态角;δVE为东向速度误差;δλ为经度误差;εE和▽N为等效北向陀螺漂移和等效北向加速度计偏置,等效东北天的元件误差与IMU的3个轴向元件误差有如下关系:
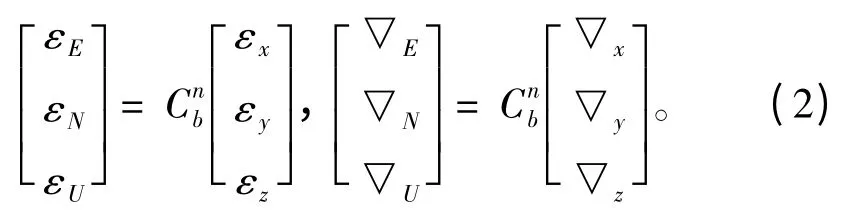
若仅考虑等效北向陀螺常值漂移,不考虑其余惯性元件输出误差、初值误差、重力加速度误差,略去航向角误差。单向通道的误差方程为:
绕航向轴旋转后,误差方程变为:

对式(3)和式(4)取Laplace 变换,方块图如图1所示。图中,陀螺常漂视为阶跃信号


图1 东向陀螺漂移与北向位置误差关系框图Fig.1 Relations block diagram of east gyro drift and north position error
由方块图求得无旋转系统误差解析式和旋转系统误差解析式如下:
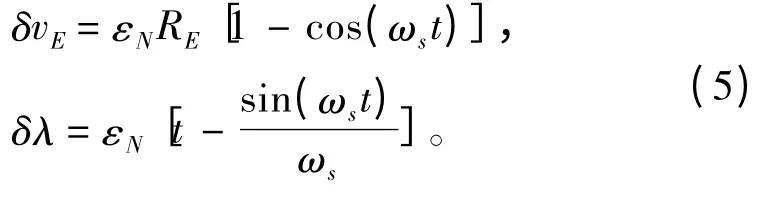

2 旋转惯导与捷联惯导误差传播特性对比分析
类似于第1 节的分析,可以得出旋转式惯导系统误差方程的解析解。这里归纳出旋转式惯导系统中器件误差引起系统误差的形式,与捷联式惯导系统对比后给出表1和表2 所列出的定性结论。

表1 单轴旋转惯导系统器件误差引起的系统误差Tab.1 The navigation errors of single axis rotation INS due to sensor errors

表2 捷联式惯导系统器件误差引起的系统误差Tab.2 The navigation errors of strapdown INS due to sensor errors
对于捷联式惯导系统,陀螺常值漂移和加计零位的影响有如下结论:
1)东向陀螺漂移εx对经度及方位产生常值分量εxtanL/ωie及εx/ωiecosL,它不引起随时间积累的误差,而对所有7个输出导航参数均产生3 种周期振荡的误差。
2)北向陀螺漂移εy及方位陀螺漂移εz引起系统误差相似,它们产生纬度常值误差分别为εysinL/ωie及-εzcosL/ωie,还产生东向速度常值误差-εyRcos2L 及-εzRsinLcosL。除了产生常值误差外,它们还产生随时间积累的经度误差-εytcosL 及-εztsinL,这也是惯导系统定位误差随时间而积累的根源,也同样对7个导航参数产生3种周期性振荡误差。
3)加计零位误差引起位置δL,δλ 及姿态误差φe,φn,φu的常值分量,而不引起速度误差的常值分量。所以惯导系统水平精度由加计零位误差所决定。
通过单轴旋转调制,将部分惯导系统器件误差调制成振荡形式,大大减小了对系统精度的影响,主要体现在:
1)通过绕天向轴旋转,与转轴垂直面上的2个等效陀螺漂移被调制:东向陀螺漂移εx对方位误差的常值误差被调制成振荡形式;北向陀螺漂移εy对东向速度和纬度产生的常值漂移被调制成振荡形式;北向陀螺v 对经度产生的随时间积累的误差被调制成振荡形式,大大减小了系统定位误差随时间积累的趋势;东向陀螺漂移v 对经度产生的常值误差εxtanL/ωie被调制掉,增加的常值误差εxtanL/ωie相比εxtanL/ωie小4个数量级。
2)加计零位误差对系统导航参数产生的常值误差均被调制成振荡形式。
3 旋转对惯性器件常值误差的调制效果分析与仿真
惯导系统误差随时间发散主要受陀螺常值漂移的影响,惯性器件常值误差是惯导系统位置误差发散的主要因素。为了验证旋转调制的效果和分析旋转惯导系统误差传播特性,对惯性器件常值误差的影响进行分析和仿真。仅考虑陀螺常值漂移=,误差项为:
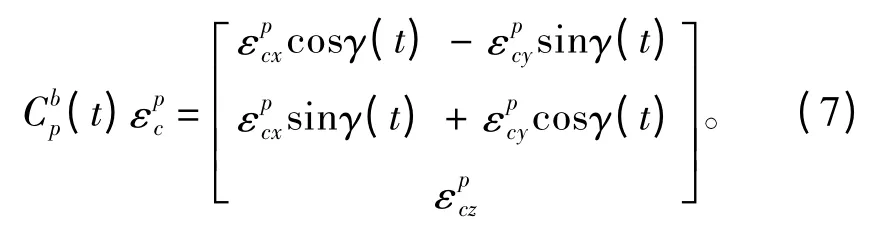
静基座下,取陀螺常值漂移[0.01,0.01,0.01]°/h,加计常值零偏[100,100,100]μg,其他误差为0。采用以下旋转方案:先绕Ozb轴正转180°,停止一段时间Ts;再反转180°,停止Ts时间;接着反转180°,停止Ts时间;再正转180°,停止一段时间Ts。以上转动次序为1个周期,之后循环不已。采样周期1 s,仿真时间64 h。旋转速度3°/s,停止时间Ts=100 s。分析旋转对常值误差的调制效果,仿真结果如图2和图3所示。
通过对比图2和图3 可见,经过单轴旋转后,零偏误差引起的导航误差得到抑制。在非旋转惯导系统中,北、天陀螺漂移引起东向速度常值误差,从而引起经度随时间积累的误差,经过单轴旋转调制,北向陀螺漂移被调制,因此经度误差被减小1/2 左右。另一方面也得出以下结论:转轴上等效陀螺漂移是限制单轴旋转惯导系统的精度继续提高的因素之一。对于双轴旋转,2个轴交替旋转,所有零偏误差均能得到调制,因此,理论上双轴旋转惯导系统不再有因陀螺漂移引起的随时间累积的发散误差项。
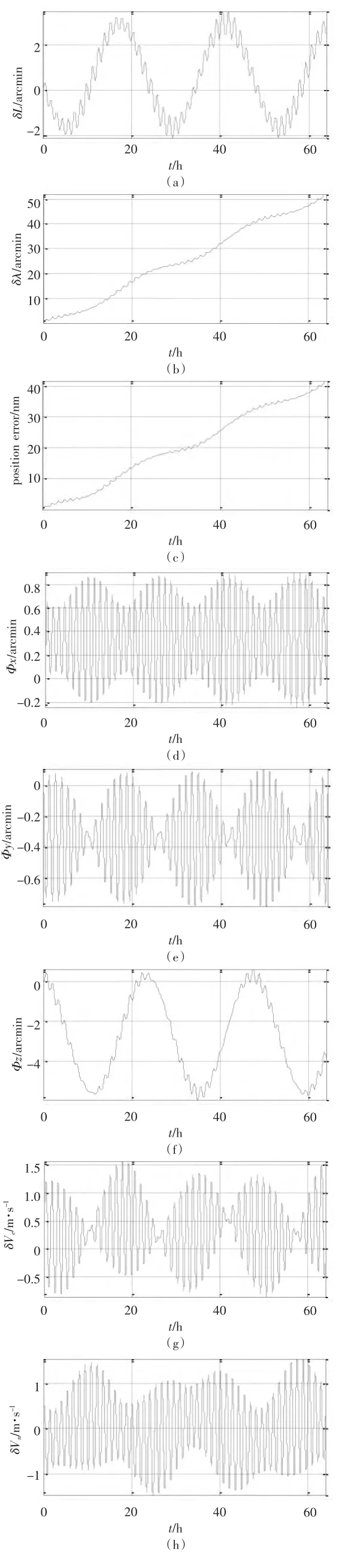
图2 仅常值误差非旋转惯导系统仿真结果Fig.2 The simulation results of non-rotation INS only considering constant errors

图3 仅常值误差旋转惯导系统仿真结果Fig.3 The simulation results of rotation INS only considering constant errors
4 结 语
本文通过对旋转惯导系统单通道误差传播特性分析,得出旋转惯导系统与非旋转惯导系统误差传播的区别,通过对比分析后,仿真验证了惯性器件常值误差经调制后对惯导的影响,得出结论如下:
1)旋转调制的本质是通过转位机构带动惯性测量单元按设计好的方案旋转,抵消惯性器件误差对导航结果的影响,从而大大提高系统的精度。
2)传统的捷联式惯导系统中,经度误差由于天向和北向陀螺漂移影响而随时间发散,经过绕天向轴旋转调制后,北向陀螺漂移对经度误差的影响被调制掉,而旋转轴方向上的陀螺漂移,即天向陀螺漂移对经度误差的影响不变。
[1]LEVINSON E,GIOVANNI C S.Laser gyro potential for long endurance marine navigation[C]// IEEE Position Location and Navigation symposium,1980:115-129.
[2]LEVISON E,MAJURE R.Accuracy enhancement techniques applied to the marine ring laser inertial navigator (MARLIN)[J].Journal of The Institute of Navigation,1987,34(1):64-86.
[3]LEVISON E,HORST J,WILLCOCKS M.The next generation marine inertial navigator is here now[C]// IEEE Position Location and Navigation Symposium,1994:121-127.
[4]TUCKER T,LEVISON E.The AN/WSN-7B marine gyrocompass/navigator[C]// ION NTM 2000.Anaheim,CA,26-28 January,2000:348-357.
[5]HIBBARD R,WYLIE B,LEVISON E.Sperry marine MK-49,The world' s best ring laser gyro ship' s inertial navigation system[C]// JSDE Proceedings.Orlando,FL,November,1996.
[6]袁保伦.四频激光陀螺旋转式惯导系统研究[D].长沙:国防科技大学光电科学与工程学院,2007.YUAN Bao-lun.Research on rotating inertial navigation system with four-frequency differential laser gyroscope[D].Changsha:College of Opto-electronics Science and Engineering,National University of Defense Technology,2007.
[7]张宇飞,陆权聪,翁海娜.基于IMU 旋转的船用激光导航系统分析与设计[J].海洋技术,2009,28(2):88-91.ZHANG Yu-fei,LU Quan-cong,WEN Hai-na.Analysis and design of marine RLG navigation system base on IMU rotation[J].Ocean Technology,2009,28(2):88-91.
[8]龙兴武,于旭东,张鹏飞,等.激光陀螺单轴旋转惯性导航系统[J].中国惯性技术学报,2010,18(2):149-153.LONG Xing-wu,YU Xu-dong,ZHANG Peng-fei,et al.Single-rotating inertial navigation system with ring laser gyroscope[J].Journal of Chinese Inertial Technology,2010,18(2):149-153.

