基于有限元法的气垫船轴系回旋振动特性计算
张 伟,吴伟亮
(上海交通大学 机械与动力工程学院,上海200240)
0 引 言
轴系回转振动的实质是转轴的进动,轴系发生回转运动时一方面围绕其几何轴线旋转,另一方面弯曲的几何轴线围绕其支撑中心线旋转。现代船舶朝着越来越大型化的方向发展,使得船体刚度下降,导致横向振动频率下降[1]。对于气垫船轴系,作为支撑体的船体浮箱刚度较弱,使得轴系的横向振动响应更为强烈,所以对气垫船轴系回旋振动的研究意义更大。
国内外学者对轴系回旋振动展开了一些研究。陈之炎等[2-3]对回旋振动的机理进行了深入地探讨,并对回旋振动计算方法进行了研究。王磊等[4]研究分析了惯性力矩、应力刚化效应及旋转软化效应等对轴系回旋振动的影响。此外,王传溥、Y Hori和Al-Bedoor B O 等[5-7]在回旋振动研究方面也做了大量工作。
本文以某气垫船垫升轴系为对象,考虑到其与传统船舶轴系的不同,需要对其回旋特性进行计算分析,通过计算了解其振动特性,为轴系安全运行提供指导。
1 力学模型
为便于分析,本文以某气垫船垫升轴系为例,建立有限元计算模型,进行有关共性问题的研究,轴系主要参数如表1所示。在有限元计算软件Ansys中建立模型,计算模型如图1所示。

图1 垫升轴系有限元模型Fig.1 The finite element model of the shafting
考虑到垫升轴系结构的复杂性,在进行船舶轴系振动特性计算时一般都要将其简化,以便于求解,针对这一轴系,作以下适当简化,计算结果显示可以反映实际振动情况:
1)选取梁单元模拟轴系轴段,弹簧单元模拟弹性支承系统的轴承。弹簧单元的一端与轴系的节点相连接,另一端设置为固定端,这样可以沿某一方向传递力或力矩。
2)风机、齿轮在有限元计算中都简化为质量单元,并考虑其转动惯量。轴段端部联轴节带有附加质量也由质量单元模拟。
3)由于法兰连接的弯曲刚度比轴的刚度大得多,直接将连接法兰作为轴段元件,忽略其弯曲变形。
4)齿轮耦合单元采用矩阵单元模拟,其平均啮合刚度取为2 ×106N/m[8]。
2 计算分析与讨论
2.1 垫升轴系回旋振动计算
轴承的支撑刚度是轴系振动特性的重要影响因素,它与很多因素有关,如轴承结构、轴承材料、轴承间隙、油膜等,所以对支撑刚度的确定是一件相当复杂的工作,一般很难单纯由计算获得。根据国内外实船数据,轴承支撑刚度在108~5 ×109N/m范围内。因此在本文中,采用考虑不同轴承支撑刚度的方法进行计算,给出转速范围的参考值。
由于垫升轴系减速器速比为1.53,垫升轴系水平分轴与竖直分轴转速不同,故分别列出其回旋振动计算结果。
当轴承刚度为1 ×108N/m,其坎贝尔图如图2所示,可以得到一次回旋转速及叶片次回旋转速。通过改变轴承刚度,计算得到不同的回旋转速,如表2和表3所示。
考虑到风机安装区域内船体刚性较弱,船体刚

图2 轴承刚度1 ×108 N/m 下垫升风机竖直分轴坎贝尔图Fig.2 Campbell diagram of the vertical shaft under the bearing stiffness of 1 ×108 N/m

表2 未考虑船体刚度时垫升轴系竖直分轴回旋振动计算Tab.2 Lateral vibration of the vertical shaft taking no consideration of the hull stiffness
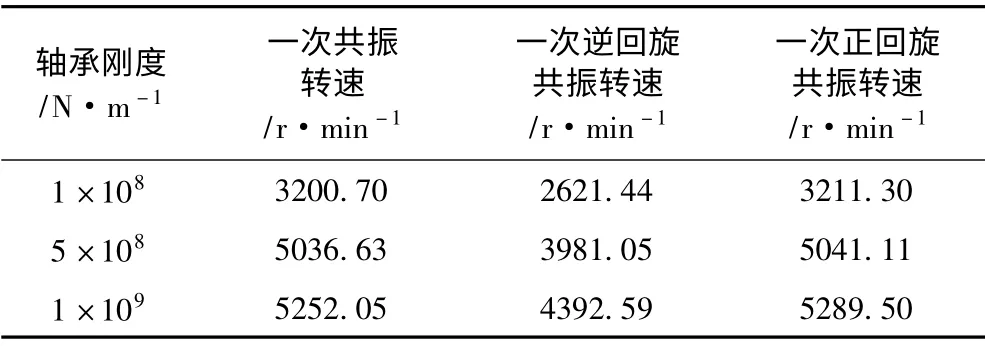
表3 垫升轴系水平分轴回旋振动计算Tab.3 Lateral vibration of the horizontal shaft
度在2 ×108~2 ×109N/m 内取值,将该船体刚度串联至风机端的上述3个刚度上,得到总的安装区域轴承刚度分布在6.7 ×107~6.7 ×108N/m 内,在此范围内取一系列刚度值,计算结果如表4所示。
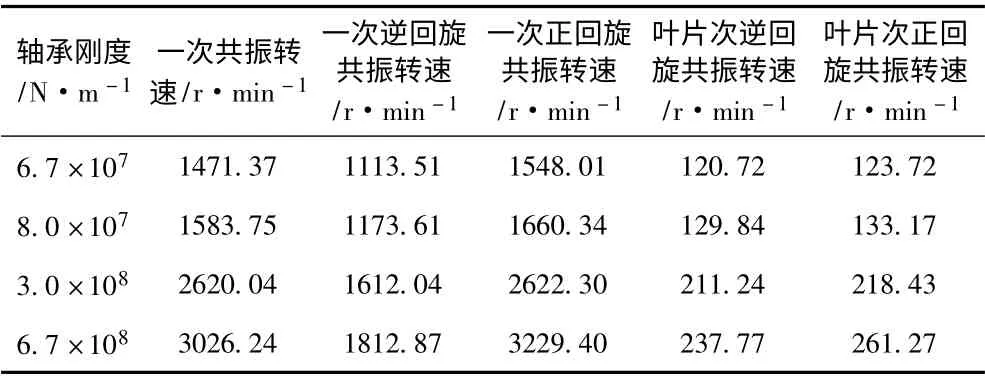
表4 考虑船体刚度时垫升轴系竖直分轴回旋振动计算Tab.4 Lateral vibration of the vertical shaft taking consideration of the hull stiffness
通过表2~表4 可看出,随着轴承支撑刚度的增大,风机轴系的共振转速逐渐升高。分析表2 可看出,在未考虑船体刚度时,垫升轴系竖直分轴一次共振转速在1 736.86~3 154.62 r/min 范围内;一次正回旋共振转速在1 809.66~3 503.13 r/min 范围内;叶片次共振转速在146.01~275.82 r/min 范围内。当考虑船体刚度时,由于串联船体刚度,总轴承刚度的下降,相应共振转速也随之下降。表4 显示垫升风机竖直分轴一次共振转速在1 471.37~3 026.24 r/min 范围内,叶片次共振转速在123.72~261.27 r/min 范围内。垫升轴系水平分轴的一次共振转速为3 200.70~5 252.05 r/min,一次正回旋转速也在3 211.30 r/min 以上。
垫升轴系竖直分轴的额定转速为850 r/min,水平分轴的额定转速在1 300 r/min,根据规定,轴系在1.15 倍额定转速下无一次回旋振动临界转速,一次叶片次临界转速不应在0.8~1.2 倍额定转速范围内,故垫升轴系回旋振动安全。
2.2 对比陀螺效应影响
对于一个带有质量的圆盘,不考虑陀螺力矩时自由振动方程

当考虑陀螺效应时,系统的运动方程中会出现一个反对称的陀螺矩阵。一般情况下,静止坐标系下考虑陀螺效应的转子系统运动方程式可写为

式中:M,C,K 分别为质量、阻尼、刚度矩阵;G为陀螺力矩。
对上述实例水平分轴进行回旋振动有限元计算,针对考虑陀螺效应与不考虑陀螺效应在不同转速下进行计算,结果如表5~表7所示。

表5 转速944 r/min 下陀螺效应对固有频率的影响Tab.5 The gyroscopic effect on natural frequency under 944 r/min

表6 转速2 360 r/min 下陀螺效应对固有频率的影响Tab.6 The gyroscopic effect on natural frequency under 2 360 r/min

表7 转速3 776 r/min 下陀螺效应对固有频率的影响Tab.7 The gyroscopic effect on natural frequency under 3 776 r/min
当轴系发生正进动时,此时陀螺力矩为正值,它使转轴的变形变小,因而提高了轴系的固有频率。反之,当发生反进动时,轴系的固有频率下降。此外陀螺效应与轴系的转速有关,转速越高,陀螺效应表现的越显著,随着轴系转速从944 r/min 到3 776 r/min,正进动差值也从0.15% 上升到0.31%。这是因为陀螺力矩包含哥式惯性力矩及牵连惯性力矩,二者都与轴系旋转角速度有关,轴系旋转角速度越大,陀螺效应也就愈显著[1]。
3 模型验证
文献[9]通过建立气垫船轴系缩比台架,进行回旋自由振动实验。针对气垫船轴系试验台架,通过Ansys 软件,采用上述简化方法对其建模计算,对比实验值与计算值,如表8所示,证明了使用有限元方法对轴系的简化计算能较好地反映振动特性,同时也说明了上述分析合理。

表8 实验与计算结果对比Tab.8 Comparison between the experimental data and the numerical results
4 结 语
本文以气垫船垫升轴系为对象,建立有限元计算模型,计算验证了陀螺效应对轴系回旋振动的影响,当陀螺力矩为正值,轴系的固有频率提高,反之下降;并分别讨论了在不考虑船体刚度及考虑船体刚度下轴系的共振转速及叶片次共振转速,对照工作转速,给出其回旋振动安全的结论,通过与文献对比,也验证了计算模型的准确性,为气垫船垫升轴系的安全运行提供了指导。
[1]陈之炎.船舶推进轴系振动[M].上海:上海交通大学出版社,1987:172-233.CHEN Zhi-yan.The vibration of ship's propulsion shafting[M].Shanghai:Shanghai Jiaotong University Press,1987:172-233.
[2]陈之炎,赵玫,骆振黄.船舶推进轴系的回旋振动[J].上海交通大学学报,1984(2):91-99.CHEN Zhi-yan,ZHAO Mei,LUO Zhen-huang.Whirling of ship's propulsion shafting[J].Journal of Shanghai Jiaotong University,1984(2):91-99.
[3]陈之炎,骆振黄,熊四昌.船舶推进轴系回旋振动计算方法研究[J].中国造船,1988(3):33-43.CHEN Zhi-yan,LUO Zhen-huang,XIONG Si-chang.A study of the calculation method of transverse vibration for ship's shafting system[J].Shipbuilding of China,1988(3):33-43.
[4]王磊,谢俊超,周瑞平.大型船舶推进轴系回旋振动特性分析研究[J].江苏船舶,2010,27(1):14-17.WANG Lei,XIE Jun-chao,ZHOU Rui-ping.Research of the lateral vibration of super ship propulsion shafting[J].Jiangsu Ship,2010,27(1):14-17.
[5]王传溥,刘志刚,张洪田,等.船舶轴系横向振动共振转速的实验[J].船舶工程,1995(4):23-24,59.WANG Chuan-pu,LIU Zhi-gang,ZHANG Hong-tian,et al.Experimental investigation of resonance speed for ship propeller shafting in lateral vibration[J].Ship Engineering,1995(4):23-24,59.
[6]HORI Y,et al.Lateral vibrations of propeller shaft systems[M].Bulletin of the Marine Engineering Society in Japan,1978.
[7]AL-BEDOOR B O.Modeling the coupled torsional and lateral vibrations of unbalanced rotors[J].Computer Methods in Applied Mechanics and Engineering,2001,190(45):5999-6008.
[8]宋雪萍,刘树英,闻邦椿.齿轮-转子系统的振动特性分析[J].机械科学与技术,2006,25(2):153-157.SONG Xue-ping,LIU Shu-ying,WEN Bang-chun.Vibration characteristics analysis of a gear rotor system [J].Mechanical Science and Technology,2006,25(2):153-157.
[9]李宁.具有弹性基础的气垫船细长轴系横向振动特性研究[D].哈尔滨:哈尔滨工程大学,2007.LI Ning.Research of lateral vibration for slightness shafting with elastic base on the hovercraft[D].Harbin:Harbin Engineering University,2007.

