政府工程多属性招投标博弈分析

吕 炜，贺昌政

(四川大学商学院，四川成都 610074)

招投标最早起源于18世纪的英国，它通过制定一套明确、具体的交易制度，并通过招投标参与人的报价来确定中标人和成交价格，以合理配置资源。中国有史料记载的招投标发生在1902年张之洞创办的湖北皮革厂，但解放前封建、半封建和半殖民地社会制度束缚了招投标事业的发展。新中国成立后，中国又实行计划经济，招投标一度停止。20世纪80年代以来，中国逐步推行招投标制度，并首先在工程建设领域予以推行，取得了显著成效。中国加入世界贸易组织后，为了与国际接轨，于2003年开始推行工程量清单计价招标，并采取国外的最低价格中标制度。但近年来，随着中国经济的快速发展，政府财力日益增强，政府投资大型基础设施项目和公益项目日益增加，而这些大型项目建设规模较大、技术复杂、建设周期长、资金占用量大，不确定影响因素较多，所需设备品种多、价值量高，因此其质量、工期和成本直接关系到整个项目的成败［1］。在这类政府工程招投标中，招标人不仅关注投标报价，还关注投标人的工程质量、工期等信息(包括竞标人资金、信用、类似工程业绩等)。传统的招投标(逆向拍卖)仅将竞标人的投标报价作为定标依据，而将工程投标质量和工期的信息作为资格审查条件，可能导致部分性价比较高的竞标人(指质量高、工期短且报价相对较低的竞标人)失去中标机会，既不利于节约政府工程采购费用，也不利于质优价廉竞标人体现其竞争优势，难以满足一些大型或技术复杂的政府工程招标的需要，因此有必要采用多属性招标。

多属性拍卖是传统拍卖的拓展，Bichler认为多属性拍卖是招标人与竞标人进行交易时考虑拍卖品的多个品质属性(如质量、交货期等)的一种拍卖方式［2］。Thiel最早研究多属性拍卖，研究如何将多属性拍卖转化为传统拍卖问题，发现在已知卖方偏好函数的情况下，多拍拍卖问题可以简化为一维采购拍卖问题［3］。根据拍卖行动规则不同，多属性拍卖又分为菜单式拍卖、选美式拍卖和记分拍卖［4］。Asker＆Cantillon证明记分制拍卖占优于菜单式和选美式拍卖［5］。Che考虑了包括价格和质量的二维拍卖模型，针对赢标人的确定和支付问题，研究了密封拍卖机制的变形协议，即第一记分拍卖、第二记分拍卖和第二首选要约记分拍卖［6］。Branco将Che的研究拓展到竞标人成本相互关联的情形，发现成本的相关性对多维拍卖最优机制有重要影响［7］。David研究了具有普遍意义的多属性拍卖［8］。王宏通过引入广义质量生产函数，求解了多维信息招投标的最优招标机制［1］。黄河假设竞标人对质量和价格分别投标，并利用树形结构求解竞胜标问题［9］。孙亚辉在David研究的基础上研究多属性拍卖方式下竞标人的最优投标策略［10］。李军和刘树林研究了基于CD效用函数的多属性采购拍卖［11］。周学广运用博弈理论研究了供应链在线多属性逆向拍卖，但其仅考虑招标人效用函数视为质量、交货期的线性函数的情形［12］。

本文将周学广研究的供应链多属性逆向拍卖方法引入研究政府工程多属性招投标，在研究David提出的招标人效用函数是价格p和品质属性的线性组合基础上，借鉴孙亚辉将招标人的效用函数视为质量等品质属性的幂函数形式［10］，即招标人效用函数是价格p和品质属性αqx的线性组合，建立了多属性非合作博弈模型，并基于该模型分析了招、投标双方的竞价策略。

一、模型

(一)问题描述

不妨考虑政府工程建设业主针对某单位工程采取多属性招标确定建筑承包商。招标文件规定投标人需要投标的多属性包括:报价、质量等级和工期。政府工程招投标流程有资格预审文件、招标文件的编制与审查、发布招标公告(或投标邀请书)、资格预审、出售招标文件、勘察现场、投标预备会议、投标文件的编制与递交、工程标底价格的报审、开标、评标、中标和签订合同。从博弈视角可将政府工程建设业主和承包商的招投标过程视为一个三阶段的动态博弈，其博弈流程如图1。第一阶段，建设业主发布某建设单位(项)工程招标公告，以及该项目建设地址、规模、详细的需求标准(招标图纸等)、工程开工日期，并提供招标工程量清单细目明细，以利于投标人评估测算是否参与该工程竞标。第二阶段，建筑承包商根据业主提供的招标文件、相关建设标准、工程量清单计价定额和设备材料市场价格等数据信息，并结合自身的施工成本、质量以及施工工期，决定其是否参与投标以及投标竞争策略。第三阶段，定标结束，建设业主或委托招标人组织评标委员会按照招标文件要求，对投标人的投标文件进行筛选和评估，以选择最佳的投标文件作为决标和授予施工合同(为简化分析，此处采取与国际招标通行的低价中标，即报价最低的投标人能够给建设业主带来最大的利润)，招标结束。因此可以将政府工程招投标视为一个多阶段的扩展式博弈，如果将所有投标人视为一个参与人，则在政府工程招标的每个阶段只有一个参与人采取行动，且其具有非简单选择集——选择集里的元素个数大于1，而其他参与人则仅有一个单元素，即“不采取任何行动”的选择集，所以可以将政府工程招投标视为具有完美信息的多阶段博弈。

图1 政府工程招投标博弈

(二)模型基本假设

Che建立了投标报价和质量的二维多属性拍卖(招标是拍卖的逆向形式)，并提出了第一记分拍卖、第二记分拍卖和第二首选要约拍卖三种形式，并证明了二维收入等价原理［6］。王宏等通过引入广义质量生产函数，把投标人的质量信息转化为综合性质量指标，求解了基于社会福利最大化的多维信息招标最优机制［1］。本文模型在Che的模型基础上参考王宏的研究内容增加了施工工期招投标属性，采用第一记分拍卖理论构建了一个更符合市场经济的基于招标人剩余最大化的政府工程多属性招标博弈模型。

假设A1:某政府工程的招投标参与人为n+1个，1个招标人(业主)和n个投标人(建筑承包商)，将其记为 N=，其中0表示招标人(即业主)。

假设A4:投标人i的施工成本是投标承诺工程质量与工期的函数，即

假设A5:政府工程招投标属于完全信息博弈，投标人之间信息对称但不存在合作，参与人的最优战略是实现效用极大化。

(三)模型

参与人i的支付等于其报价减去工程成本，结合假设A4可得竞标人i的利润函数:

(2)式中，k1、k2是投标人完成拟投标工程单位质量成本和工期成本系数，对投标人i来说k1、k2为已知常数。

从概率论角度看，政府工程投标参与人赢得中标具有一定概率，记为，即n个投标人参与竞标，投标人i按组合投标且其提供给招标人的效用U*最大时的概率。投标人i期望支付为:

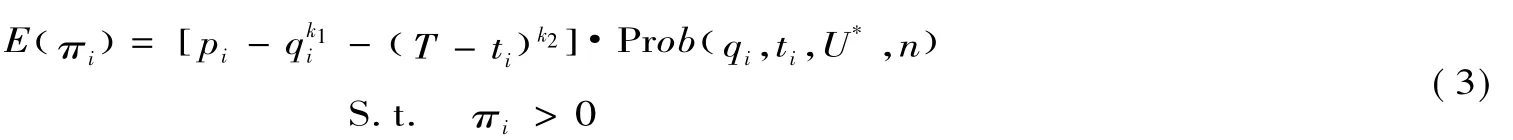
二、动态博弈求解及分析

(一)均衡招投标策略

政府工程招投标活动中，所有参与人对自己选择前的博弈过程完全了解，而在每一阶段，仅有一个参与人具有1个以上的行动空间，其他参与人不采取任何行动，因此属于一个三阶段完全且完美信息动态博弈，采用逆向递归法(Backwards Induction)可以求解其子博弈纳什精炼均衡(subgame perfect Nash equilibrium)［13］。

首先，考虑博弈的最后一个阶段(即第3阶段)，子博弈完美纳什均衡策略应是招标人选择使他效用最大的竞标人。不妨设第i个投标人能够使招标人获得的效用最大，即第i个投标人的投标策略满足:

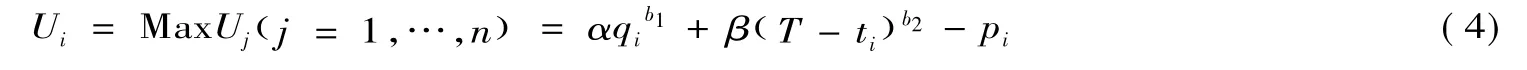
其次，在第二阶段，每个投标参与人根据建设标准、工程量清单计价定额和设备材料市场价格等信息，并结合其施工成本、质量以及工期等，选择一个使其利润极大化的投标价格。能够赢得中标的是能给招标人带来最大效用的投标人。因此满足上述两个条件的投标策略才是子博弈纳什均衡解。

由假设A2知，投标人i的类型函数可由施工质量qi和工期ti表述，故竞标人i的类型函数为而招标人的效用与竞标人i的投标报价、施工质量和工期正相关，且投标人的报价是其施工质量和工期的函数，因此可将投标人带给招标人的效用视为竞标人的投标报价得分，因此可用si和Θi分别代替投标人的投标报价得分和类型。

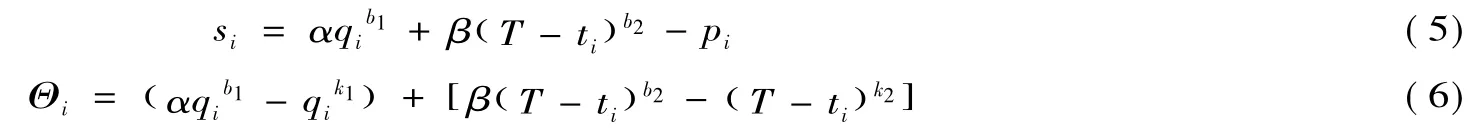
将(5)、(6)式代入(3)式，可得第i个投标人的最优均衡策略为:

(二)子博弈精炼纳什均衡

不妨考虑类型函数为Θi的竞标人i的策略，投标价格为其施工质量和工期的函数并将其记为B，即类型函数为Θj的投标人j，其报价表示为显然B是单调递增函数，即类型越好的投标人带给招标人的效用就越大，竞争能力越强，其投标得分越高。如果投标人i赢得中标，那么其报价得分应该满足si＞sj，j≠i，且j=1，2，…，n。竞标人i投标得分为si，且赢得中标的概率为其他所有竞标人投标得分满足si的概率。因此，其中B－1()·是B()·的反函数。投标报价得分为si的竞标人i的期望支付为:

对投标人i来说，子博弈精炼纳什均衡就是选择最优投标得分s*i，故将(9)式两端对si求导并令其等于零，即

然后将(9)式两端对Θi求导可得

将si=和(10)式代入(11)式整理可得:

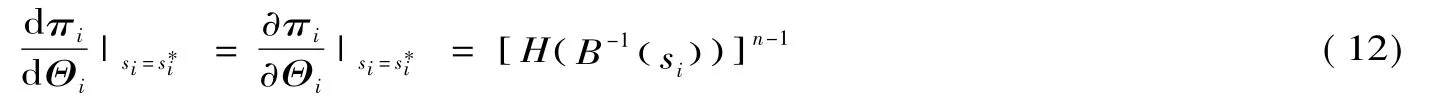
根据假设A5，投标人信息相互对称，所有参与竞标人的投标函数B均满足(9)式期望利润最大化条件，因此投标报价得分相同的竞标人具有相同类型，即存在子博弈精炼纳什均衡条件下si=BΘ()i，将其代入(12)式可得:

将(13)式两端对 Θi进行积分，可得

最后求出投标人的投标报价策略:

由(16)式知，最优投标策略由两部分构成:一是投标人完成拟投标工程的施工成本，即二是投标人类型优势带来的超额利润，即。且其最优报价策略是其成本的函数。

命题1:在政府工程招投标非合作博弈模型中，竞标人存在子博弈精炼纳什均衡策略，即为(16)式。

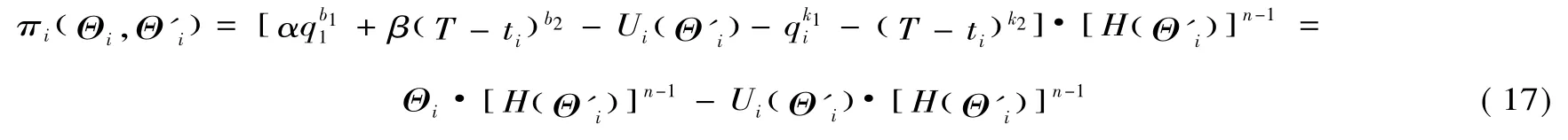
再将(17)式两端对Θ'i求偏导数可得:

类型为Θi的投标人i假装类型Θ'i投标人参与竞标，招标人获得的期望剩余:

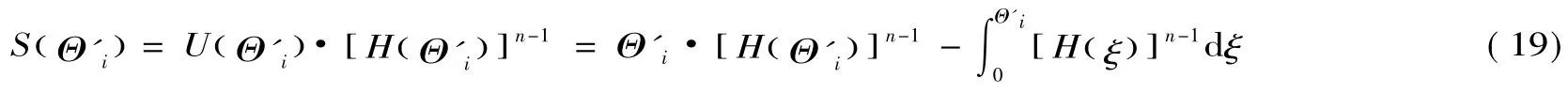
将(19)式两端对Θ'i求导可得:

把(20)式代入(18)式整理可得:

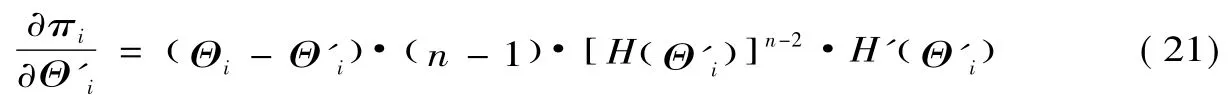
由命题1知，对理性的竞标人来说都不应假装其他竞标类型，而应按其真实的产品质量和提前工期投标，其投标价格策略为(16)式，即竞标人主动向招标人透露其真实的质量和提前工期。

(三)投标人竞标策略性质

命题2:公开招标人偏好的政府工程多属性招投标博弈模型中，竞标人收益与投标质量和工期的图形关系分别呈U形，即投标质量和提前工期分别超过某点后，投标人的收益分别是其投标质量和提前工期的增函数;而在到达该点之前，投标质量和提前工期边际收益递减。

证明:不妨考虑竞标人i在某政府工程招投标活动中，其投标承诺质量为、提前工期为ti。子博弈精炼纳什均衡时，竞标人i按(16)式进行投标报价，因此将(16)式代入(3)式可求得投标人i的期望支付:

将(22)式两端对qi求偏导可得:

k1=1，当qi＞

k1≠ 1，当 qi＞

因此，招标人收益与投标质量的关系为:(1)k1=1，当投标质量时，竞标人收益是其质量的增函数;当投标质量时，竞标人收益是其质量的减函数。(2)k1≠1，当时，竞标人收益是其质量的增函数;当时，竞标人收益是其质量的减函数。

再将(22)式两端对ti求偏导可得:

但对理性的竞标人i来说:当k2≥b2时，竞标人i将放弃竞标，因其参与工期成本大于招标人的质量效用，因此k2＜b2。

k2=1，当ti＞T－

k2≠1，当 ti＜ T－0;当ti＞T－

因此，招标人收益与投标工期的关系为:(1)k2=1，当投标提前工期时，竞标人收益是其竞标提前工期的增函数;当时，竞标人收益是其投标工期的减函数。(2)k2≠1，当竞标提前工期时，竞标人收益是其竞标提前工期的减函数;当时，竞标人收益是其竞标提前工期的增函数。

综上，在投标质量和提前工期分别超过某点后，投标人的收益分别是其投标质量和提前工期的增函数，即投标类型越好的竞标人更能体现其竞争优势，获得更多的收益;而在到达该点之前，投标质量和提前工期边际收益递减。这一点与周学广等人的研究结论略有不同［12］，但本文的研究结论更符合实际，因为在政府工程招投标实践中，当招标人要求的质量和提前工期超过国家规定的合格标准之后，他必须额外支付投标人为完成高质量工程和赶工工期(提前工期)的费用。

推论1:公开招标人偏好的政府工程采用多属性招投标博弈，招标人的投标承诺质量和提前工期偏好系数越大，竞标人的收益越高。

证明:将(22)式两端对b1求导可得，因此，投标人的收益是招标人质量偏好系数的增函数(显然qi＞1，因政府工程采用多属性招投标时，理性竞标人的投标承诺质量高于国家最低质量等级)。

将(22)式对b2求导可得，即投标人的收益是招标人提前工期偏好系数的增函数(显然ti＜T－1，因在招投标实践中，竞标人承诺的提前工期通常大于1天)。

综上，招标人的承诺质量和提前工期偏好系数越大，竞标人的收益越高。此结论与命题2表面上看似相矛盾，但实际上当招标人的投标承诺质量和提前工期偏好系数足够大时，竞标人的承诺投标质量和提前工期肯定超过命题2中的极小值点，推论1与命题2并不矛盾，二者实际上是一致的。

由推论1知，竞标人的收益与招标人承诺质量和提前工期偏好系数成正相关，因此理性竞标人的类型越好越愿意参加招标人非价格偏好系数越高的政府工程招投标，以充分发挥其类型竞争优势，获得更高的期望收益。

(四)招标人剩余的性质

命题3:在公开招标人偏好系数的政府工程招投标活动中，若竞标人均按(18)式进行投标，招标人的剩余效用与投标质量和工期的图形关系呈U形，即当投标质量和提前工期超过某点后，招标人剩余是投标质量和提前工期的增函数，而在到达该点之前，招标人剩余是投标质量和提前工期的减函数。

证明:将(16)式代入(1)式即可求出招标人的消费者剩余:

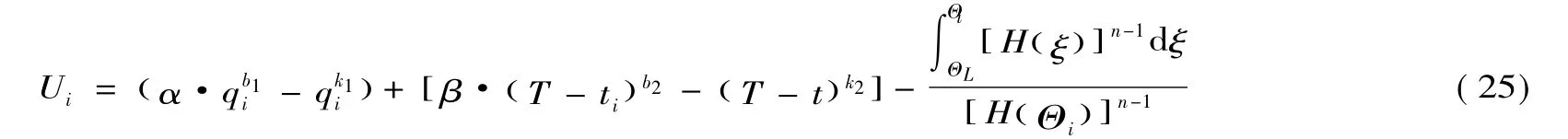
将(25)式对qi求偏导可得，，其中，均衡时投标人i中标的概率为零，不予考虑)，因此:当时，0; 当 qi=时 ，;当

再将(25)式对 ti求导可得，，因此当当ti＞T－

综上，当竞标人承诺投标质量和提前工期超过某点后，招标人剩余是投标质量和提前工期的增函数，而在到达该点之前，招标人剩余是投标质量和提前工期的减函数。

由命题3知，对政府工程招标人来说，制定合理的招标规则(包括选择合适的记分函数)，以使竞标人的投标质量、提前工期和价格策略分别按和(16)式予以确定，将有利于提高其招标剩余，因此合理制定多属性招标规则具有十分重要的意义，因其事关招标人剩余大小。

推论2:竞标人施工质量和工期成本系数值越大，招标人剩余越小。

证明:将(25)式对k1求导得，再将(25)式对k2求导得，因此，招标人的消费者剩余是竞标人施工质量和工期成本系数的减函数。

由推论2知，招标人的剩余与竞标人投标质量和工期成本系数成反比，因此招标人选择合理的记分函数，可以降低施工质量和工期成本系数较高的竞标人得分，有助于提高招标剩余。

推论3:政府工程采用多属性招投标时，招标人的投标承诺质量和提前工期偏好系数越大，其招标剩余也越大。

证明:将(25)式两端对b1求偏导可得，;再将(25)式两端对 b2求偏导可得，因此，招标人剩余是招标人投标承诺质量和工期偏好系数的增函数，即招标人的工程质量和工期偏好系数越大，其获得的消费者剩余也越大。

由推论3知，竞标人认为招标人的质量和提前工期偏好系数越大，就能使招标人获得更多的招标剩余，因此理性的招标人更愿意通过诱导竞标人相信其质量和提前工期偏好系数较大而获得更多的招标剩余。

(五)参与人的最优策略

命题4:参与政府工程多属性招投标博弈的参与人的最优策略分别为:竞标人根据其真实施工质量和工期水平进行投标，其投标报价为(16)式;招标人则是根据竞标人投标的施工质量和工期的最优组合来确定获胜者。

证明:由命题1知，竞标人的最优投标博弈策略是按其真实的施工质量和工期进行投标，其投标报价为(16)式。又由命题3知具有高施工质量和较大提前工期周期的的竞标人能给招标人带来更多的招标剩余，因此招标人应根据投标质量和工期的最优组合来确定获胜者。

因此，均衡时竞标人的最优策略是按(16)进行投标报价，并按其施工质量和工期进行投标，这种招投标方式有利于招标人根据竞标人投标性价比择优确定赢标人，提高政府工程招投标效率。其原因是招标人可以直接根据投标质量、工期和价格的最优组合确定政府工程承包商，且质量好、工期短的竞标人不仅能够增加招标人的消费者剩余，而且还能增加其自身收益，故对一些技术复杂的工程采用多属性招投标能增大招、投标双方效用，从而实现双赢。

三、算例验证

假设某政府工程采取多属性招标，建设业主通过招标文件给出其质量、工期的权重系数α=0.6，β=0.5，最低投标质量Q=0.3，最长工期T=1，并告知其质量和工期的偏好系数分别为b1=2.2，b2=1.9;不妨考虑参与竞标的投标人数n=5，竞标人i完成该工程的质量和工期的成本系数k1=1.5，k2=1.2，且竞标人的质量和工期ti独立且在区间0，()1上服从均匀分布。

(一)投标价格与工期、质量关系

由(16)式可以得到竞标人i的投标价格:

用Matlab可绘出(26)式的图形，即竞标人投标报价与质量、工期关系图，见图2。

由图2知，当竞标质量或提前工期即将接近极限点(即质量即将达到最高质量等级、提前工期接近最短工期时)，竞标人的投标价格急剧上升，因竞标为达到质量和工期的极限点，其成本急剧上升，需要提高投标报价弥补工程成本，与现实实际相符。

图2 投标报价与质量、工期关系

(二)招标人剩余与投标质量与工期的关系

根据(25)式和算例中数据，用Matlab绘出招标人剩余与质量、工期关系(图3)。

表面上看图3的形状与命题3的结论不一致，但将算例中给定的数据带入(25)式，即招标人剩余随竞标质量边际递减;同理将算例中给定的数据带入(25)式，即招标人剩余随竞标提前工期边际递减。即图3仅反映了招标人剩余与投标质量、工期递减部分的关系，因此二者之间并不存在矛盾。

图3 招标人剩余与投标质量、工期关系

(三)根据(22)式和算例提供的数据，运用Matlab可得到竞标人收益与质量、工期的关系(图4)

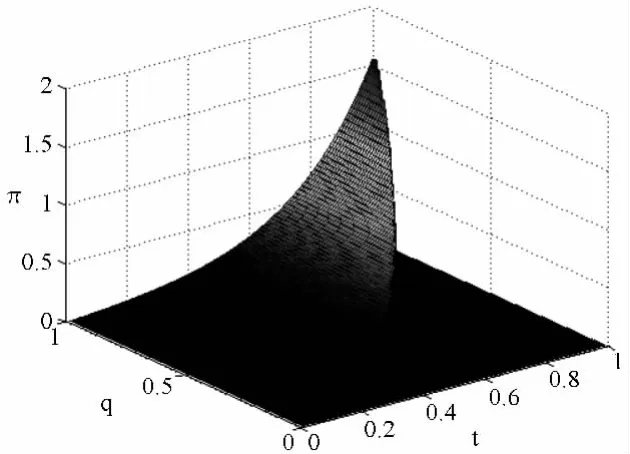
图4 竞标人收益与投标质量、工期关系

由图4知，竞标人缩短工期增加的收益比提高质量产生的收益显著得多。

(四)招标人剩余与竞标人质量、工期成本的关系

根据(25)式和算例数据，运用Matlab可得到招标人剩余与竞标人质量、工期成本的关系(图5)，其反映的结果与推论2的结论完全一致。

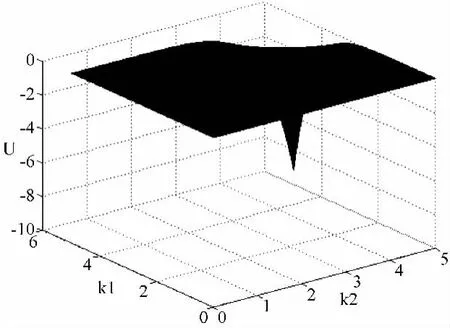
图5 招标人剩余与竞标人质量、工期成本关系

(五)招标人剩余与竞标人质量、工期偏好系数的关系

根据(25)式和算例数据，运用Matlab可绘出招标人剩余与质量、工期成本的关系(图6)，其反映的结果与推论3的结论完全一致。

图6 竞标人质量、工期成本关系

四、结论

本文将政府工程多属性招投标视为一个招标要约、投标承诺和定标的三阶段动态博弈问题，并构建了非合作动态博弈模型。该模型考虑了投标价格、工期和质量三个属性，将竞标人的类型函数通过质量和工期予以表示，并将投标价格视为质量、工期的函数，利用逆推法求解了该模型子博弈纳什均衡。在子博弈纳什均衡时，竞标人会根据自身真实的施工质量和工期进行投标，并进一步得出招标人剩余效用和竞标人收益分别与投标质量、工期的图形呈U形，即投标质量和提前工期分别超过某点后，投标人的收益分别是其投标质量和提前工期的增函数;而在到达该点之前，投标质量和提前工期边际收益递减;招标人的投标承诺质量和提前工期偏好系数越大，竞标人的收益越高，因此竞标人的投标也越积极，招标人的剩余也越大;竞标人施工质量和工期成本系数值越大，招标人剩余越小。

论文构建的政府工程多属性招投标博弈模型是建立在公开招标人偏好系数的基础上，而现实政府工程招投标信息通常难以满足此条件，因此针对此问题可进一步深入研究。

［1］王宏，陈宏民，杨剑侠.多维信息招投标中的最优机制及其实施［J］.管理科学学报，2010，13(08):1-14.

［2］BICHLER M.An experimental analysis ofmulti-attribute auctions［J］.Decision Support Systems，2000，29(3):249-268.

［3］THIEL SE.Multidimensional auctions［J］.Economics Letters，1988，28(1):37-40.

［4］唐邵玲，刘琳.两种记分函数下多属性拍卖投标均衡策略［J］.经济数学，2011(2):54-59.

［5］ASKER J，CANTILLON E.Properties of scoring auctions［J］.The RAND Journal of Economics，2008，39(1):69-85.

［6］CHE Y K.Design competition through multidimensional auctions［J］.rand Journal of Economics，1993，24(6):68-80.

［7］BRANCO F.The design ofmultidimensional auctions［J］.The RAND Journal of Economics，1997，20:63-81.

［8］DAVID E，AZOULAY-SCHWARTZ R，KRAUSS.Bidding in sealed-bid and Englishmulti-attribute auctions［J］.Decision Support Systems，2006，42(2):527-56.

［9］黄河，徐鸿雁，陈剑.多因素采购组合拍卖获胜者确定问题研究［J］.系统工程理论与实践，2008，28(7):27-33.

［10］孙亚辉，冯玉强.多属性密封拍卖模型及最优投标策略［J］.系统工程理论与实践，2010(7):1185-9.

［11］李军，刘树林.基于Cobb-Douglas效用函数的多属性采购拍卖［J］.管理科学学报，2012(3):54-60.

［12］周学广，张坚，梅强，等.基于多属性逆向拍卖的博弈分析［J］.管理工程学报，2011，25(2):200-5.

［13］FUDENBERG D，TIROLE J.Game theory.1991［M］.Cambridge，MA:MIT Press，1991.