基于响应面方法的支架结构模型修正研究
邱飞力,张立民,张卫华,高荣荣
(西南交通大学 牵引动力国家重点实验室,成都 610031)
基于结构动力的有限元模型直接修正方法存在两大缺陷[1,2]:
(1)通过理论计算值与实测值的残差建立目标函数,应用优化算法进行迭代求解。因此,每次迭代均需要调用有限元模型,导致了修正时间较长,计算量大。对于修正参数较多的结构,需要无数次的有限元计算,不易实现。
(2)直接修正法主要基于参数灵敏度分析,即计算单参数在某个设计点的灵敏度(局部特征灵敏度),没有考虑多因素同时参与变化的影响,以此选取修正参数缺乏合理性[3―5]。
响应面方法是一种统计理论与模型修正技术相结合的方法。响应面法仅通过有限次的有限元计算,拟合出结构响应与参数的显式函数,并以此替代有限元模型。从而避免了灵敏度分析,提高修正效率,更加具有优越性[6]。同时,响应面方法采用显著性分析选取参数,在整个设计空间中挑选设计参数,克服了灵敏度分析的缺陷。
1 响应面方法
1.1 试验设计
在众多的样本空间设计方法中,中心复合设计应用最为广泛[7―9]。因而采用中心复合设计法安排试验,首先根据m个因素±1的两个水平,用正交表构建2m。由于数值计算不存在物理试验的不确定性,故对中心点(0,0,0,…,0)仅作一次试验。然后在每个因素的坐标轴上,取臂长为±a的两个对称点作试验样本,m因素共2m个试验点[10]。
中心复合设计样本点总数为

臂长a取值关系式为

式中n是正交试验次数。中心复合设计是超定设计,即样本数目大于多项式未知系数个数。
1.2 显著性分析
响应面方法的参数选取是基于显著性分析理论。与灵敏度分析方法相比,显著性分析从全局角度出发,能够在整个设计空间中选取对特征量影响显著的参数。
显著性分析采用统计学的F检验法,利用F值进行假设检验,找出对结构响应影响显著的参数,统计量F的计算式如(3)所示[1]

式(3)中,SSE(x1,x2,...,xm-1)为包含m-1个自变量的回归模型误差平方和;SSE(x1,x2,..,xm)为包含m个自变量的回归模型误差平方和,k为回归模型变量个数。
若取显著水平∂,则有

式(4)中,Fj由式(3)计算可得,F1-∂表示F检验临界值,(1,n-m-1)分别表示单个变量n-m-1个自由度,P表示概率。
当P≤∂时,变量对响应的影响显著;反之P≥∂时,变量对响应的影响不显著。
1.3 响应面函数拟合
响应面函数是系统响应与输入参数之间关系的描述。响应面表达式的待定系数应尽可能越少,以减少样本试验次数。
2阶多项式拟合响应面函数最为常用,其表达形式如(5)式所示[11,12]

对响应面函数采用R2判定系数和相对均方差(RMSE)检验其精度,其计算式子分别如(6)和(7)所示[13,14]

式中yRS(j)代表单次响应面模型计算值,y(j)代表响应的有限元计算结果表示有限元分析平均值,N代表设计空间的检验点数。
R2表示响应面模型在设计空间内描述响应与参数之间关系的准确程度,RMSE表示响应面模型与有限元计算的差异程度。
2 有限元模型误差分析[15]
2.1 有限元模态分析
支架结构的几何模型及各组成部件编号如图1所示。
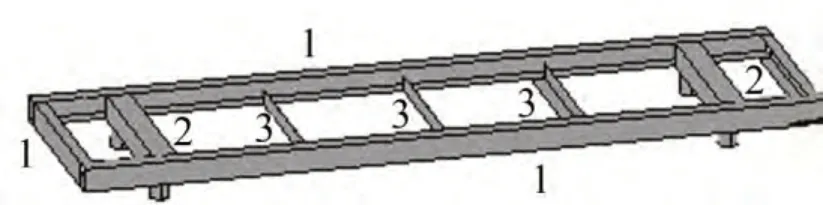
图1 支架结构几何模型图
支架结构有限元模型主要的原始参数如表1所示。
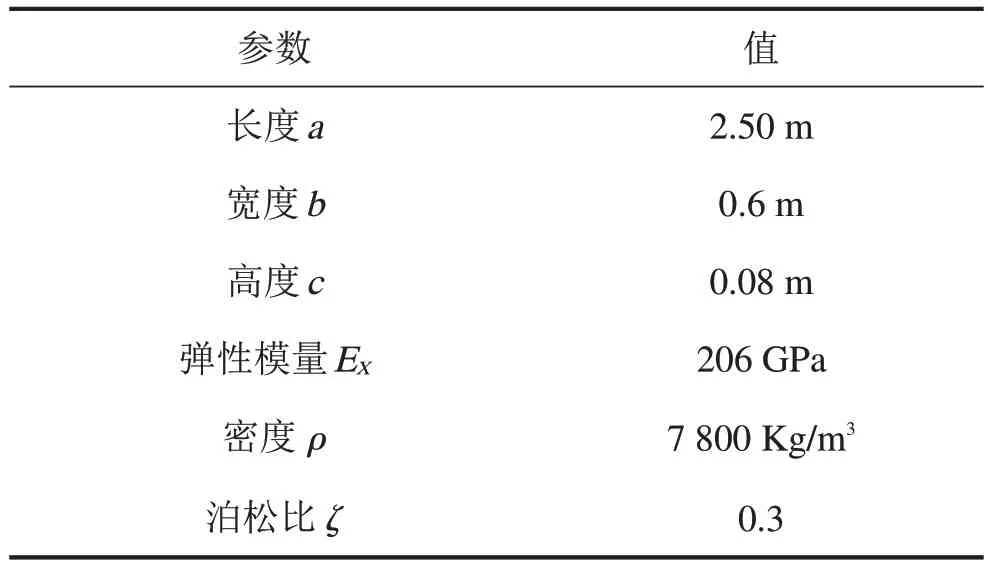
表1 支架模型原始参数表
对支架结构进行有限元模态分析(FEA),有限元分析(FEA)的模态参数如表2所示。
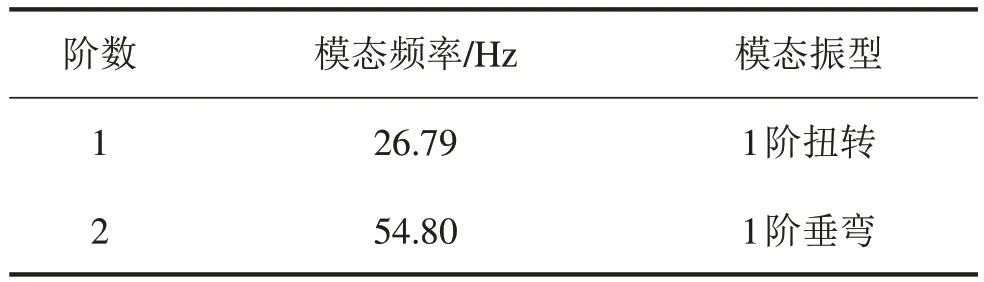
表2 有限元(FEA)模态参数表
2.2 试验模态分析
结合有限元模态分析(FEA)结果,在支架上总共布置12个测点,分别位于支架的八个顶角和中部上下表面。支架采用刚度较小的弹簧支撑模拟自由状态,其现场测试照片如图2所示。

图2 支架测试照片
应用振动噪声测试软件LMS test.lab进行模态测试分析,支架的实验模态分析(EMA)参数如表3所示。

表3 实验模态(EMA)参数表
2.3 误差分析
有限元模型修正前,先进行实验模型与有限元模型匹配。支架结构振型匹配后的频率与MAC值如表4所示。

表4 支架模态参数匹配结果
由表4可见,有限元模型与试验振型MAC非常高,表明了振型形态吻合。但频率值存在较大的误差,其最大误差达到7.8%。
3 有限元模型修正
3.1 样本试验设计
选取支架结构模型的3个部件的弹性模量(EI1,EI2,EI3)和密度参数(ρ1,ρ2,ρ3)作为修正参数。针对密度误差相对较小,取(1±5%)范围作为密度参数取值范围,弹性模量误差较大,选取(1±20%)范围作为弹性模量参数取值范围,如表5所示。

表5 修正参数参数范围
根据中心复合法,进行6参数的试验样本设计,并代入有限元模型求取样本值(1阶扭转和1阶垂弯频率),样本点组成如表6所示。

表6 样本点组成表
表6中±1分别代表对应参数的最小值和最大值,0代表参数的中间值,对应于表5和表6。6参数的中心复合设计共77个样本点和77个样本值。由于篇幅有限,此处未给出所有样本点和对应的样本值。
3.2 显著性分析
针对试验设计中的77个样本数据,对6参数及其交叉项进行显著性分析。借助软件Designexpert,检验各参数对结构1阶扭转频率和1阶垂弯频率的显著性,如图3和图4所示。
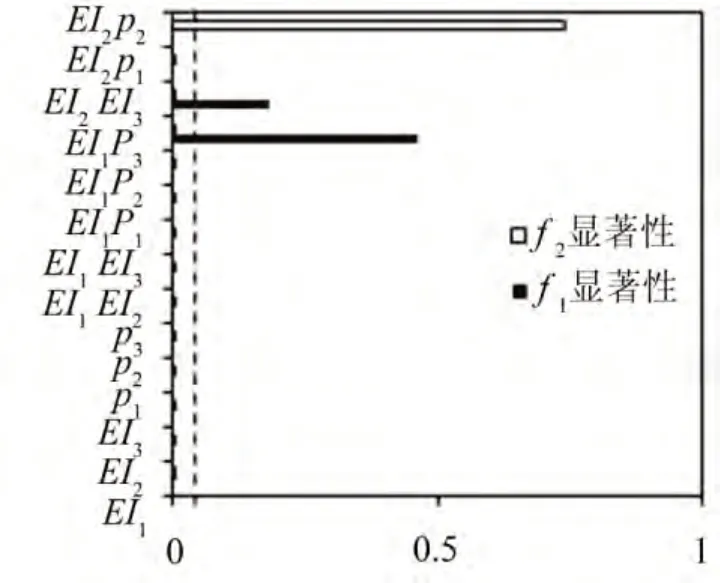
图3 参数显著性
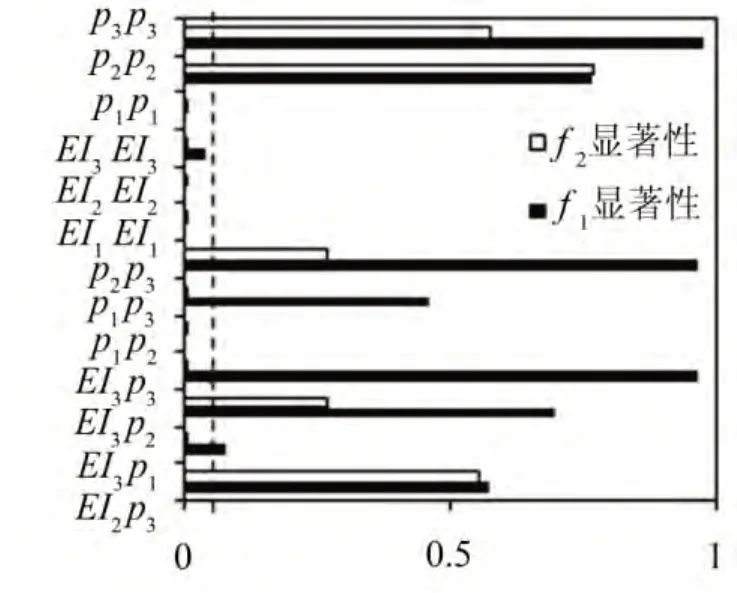
图4 参数显著性图(续)
在图3和图4中垂直细虚线位置为a=0.05。由图可知,3个部件的弹性模量(EI1,EI2,EI3)和密度参数(ρ1,ρ2,ρ3)对1阶扭转和1阶垂弯频率影响显著,因此选取6个参数均选取修正变量。同时发现,部分交叉项对1阶扭转和1阶垂弯频率影响不显著,忽略其影响从而简化响应面模型,提高计算效率。
3.3 响应面拟合
根据选取的显著修正参数,忽略影响不显著的交叉项。利用Design-expert软件,对样本数据进行响应面的二次多项式拟合。同时采用matlab编写程序进行验证,两者对比表明matlab程序与Designexpert拟合结果完全一致。支架结构1阶扭转频率f1和一阶垂弯频率f2的响应面拟合式分别如(8)和(9)式所示

为检验响应面模型的精度,根据式子(6)和式子(7)计算R2和RMSE,如表7所示。

表7 响应面精度检验值
从表7中可知,1阶扭转、1阶垂弯响应面函数的判定系数R2均为1.00,表明响应面模型能够准确描述1阶扭转、1阶垂弯频率与修正参数间的关系;且两者的RMSE值均很低,验证了回归模型具有非常高的精度,能够替代有限元模型完成模型修正。
1阶扭转和1阶垂弯频率的响应面函数属于多元多项式,保留其中两项,其余项置于零水平(即参数赋为中间值),以EI1、EI2为例绘制三维响应面如图5和图6所示。
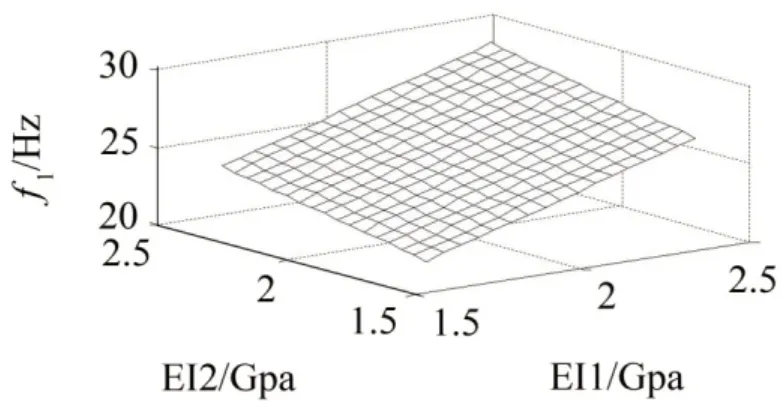
图5 1阶扭转频率响应面

图6 1阶垂弯频率响应面
在其余参数保持不变情况下,通过图5和图6可以看出EI1、EI2两因素变化对1阶扭转、1阶垂弯频率的影响趋势。
3.4 模型修正
利用拟合的响应面函数,模型修正过程转化成对优化问题(10)的求解。

修正前后的参数值对比如表8所示。

表8 修正前后参数对比值
将修正后的参数值代入模型中计算,得到的修正后的1阶扭转和1阶垂弯频率,与实测值比较如表9所示。

表9 修正后频率与实测频率对比表
从表9可以看出,修正后的1阶扭转频率最大误差为3.4%,不超过5%;修正后1阶垂弯频率误差仅为0.05%,与实测值保持了高度一致。且振型MAC值均高于90%,振型形态一致。由此表明了响应面方法能够准确地完成模型修正,且仅利用2阶多项式进行计算,不需要重复调用有限元模型。
3.5 修正效率
结合文献[15]中的灵敏度修正研究,在同一待修正模型且均选取了6个修正参数情况下,两种方法调用有限元模型的次数对比如表10。

表10 两种修正方法调用有限元模型次数对比
由表10可以看出,针对于支架有限元结构两阶待修正模态频率情况,响应面调用有限元模型次数较灵敏度分析方法少。若待修正模态阶数增加,灵敏度分析方法调用模型次数将成倍增长,而响应面方法调用模型的次数保持不变。
4 结语
(1)利用响应面方法修正支架有限元模型,修正后1阶扭转频率与误差为3.4%,1阶垂弯频率误差仅为0.05%,说明修正后的模型准确能够反映支架的实际结构。同时也验证了响应面方法在有限元修正中的可行性与准确性。
(2)采用中心复合方法,进行试验样本设计,无需对6个设计参数所有的组合进行计算,减少了试验样本数目,降低了计算量。
(3)基于显著性分析的参数筛选方法,能够在整个参数设计空间上选取对修正目标影响显著的参数和参数交叉项,简化响应面模型,较灵敏度分析方法能更加合理地提高修正效率。
(4)回归分析拟合的2阶响应面模型,有效地代替了支架的有限模型进行修正。与灵敏度方法比较,避免修正迭代过程中重复调用有限元模型,极为迅速地完成模型修正,具有重要的现实意义,尤其适用于网格单元数目庞大、待修正模态阶数较多的有限元模型修正。
[1]宗周红,任伟新.桥梁有限元模型修正和模型确认[M].北京:人民交通出版社,2012:107-108.
[2]李伯灵,荣克林.基于响应面的多目标有限元修正技术研究[J].强度与环境,2010,37(4):13-21.
[3]隋允康,张立新,等.基于响应面方法的桁架截面灵敏度分析和优化[J].力学季刊,2006,27(1):96-102.
[4]邓苗毅,任伟新.基于响应面方法的结构有限元模型修正研究进展[J].铁道科学与工程学报,2008,5(3):42-45.
[5]Ozaki I,Kimura F,Berz M.Higher-order sensitivity analysis of finite element method by automatic differentiation[J].Computational Mechanics,1995,16(4):223-234.
[6]段 巍,赵 峰.结构可靠性灵敏度分析的响应面方法比较研究[J].中国机械工程学报,2009,7(4):392-401.
[7]Douglas C.Montgomery.Design and analys is of experiments(实验设计与分析)[M].中国统计出版社,1998.
[8]席 光,王志恒,王尚锦.叶轮机械气动优化设计中的近似模型方法及其应用[J].西安交通大学学报,2007,2(41):125-135.
[9]赵祖德,陈学文,陈 军,等.基于近似模型和数值模拟的连杆热锻成形工艺设计优化[J].上海交通大学学报,2008,5(42):748-751.
[10]吴佳燕,李郝林.基于响应面法的主轴系统热特性有限元模型参数修正[J].机械设计与研究,2010,26(7):21-24.
[11]GUO Qiang-hui,GUO Li-ping,WANG Zhi-ying,ZHUANG Yan,GU Zhen-xin.Response surface optimization and identification of isothiocyanates produced from broccoli sprouts[J].Food Chemistry,2013,141(3):1580-1586.
[12]王彬星,郑四发,等.驾驶室声场响应面仿真模型的构建及应用[J].噪声与振动控制,2011,3:60-64.
[13]Abdorreza Mohammadi,Vahid Ghasemzadeh-Mohammadi,Parivash Haratian,Ramin Khaksar,Maryam Chaichi. Determination of polycyclic aromatic hydrocarbons in smoked fish samples by a new microextraction technique and method optimization using response surface methodology[J]. Food Chemistry,2013,141:2459-2465.
[14]LIU Xing-li,MU Tai-hua,SUN Hong-nan,ZHANG Miao,CHEN Jing-wang.Optimisation of apueous twophase extraction of anthocyanins from purple sweet potatoes by response surface methodology[J].Food Chemistry,2013,141(3):3034-3041.
[15]邱飞力,张立民,等.基于设计参数的支架结构模型修正[J].噪声与振动控制,2014,34(1):36-40.

