基于统计能量法的飞行器结构声振响应分析

张国军，闫云聚，李鹏博

（1.西北工业大学 力学与土木建筑学院，西安 710129；2.第二炮兵工程大学 理学院，西安 710025）

高速飞行器在发射和飞行过程中要经受复杂和严酷的力学环境。在研制初期，飞行器力学环境预示是设计和试验过程中迫切需要解决的关键环节之一，同时，飞行器力学环境预示也是飞行器及其设备设计和地面验证试验的主要依据。不符合实际情况的力学环境预示结果会给飞行器研制经费、进度、可靠性带来重大影响，直接影响到飞行器设计水平的提高，甚至对研制成功与否都有很大的影响。

传统的模态分析方法如有限元等在解决工程结构系统的动力学问题的应用已有很久的历史了，但是这些方法仅局限于对能够清晰辨认的有限数量的低阶模态进行分析，分析误差随着频率范围向更高扩展而增加，分析难度随着结构复杂程度而增加，尤其是高阶模态参数的不确定性，该方法就显得无力。因此，使用统计模态的概念，把振动能量作为描述振动的基本参数，并根据振动波和模态间存在着的内在联系，建立分析声、结构振动和其它不同子系统耦合动力学的统计能量分析方法就更具优势。该方法适用于分析含高频、高模态密度的复杂系统（包括声与结构、结构与结构）的耦合动力学问题，例如使用统计能量分析预示复杂系统的内外声振环境问题[1]。

刘海生等[2]从声振系统激励和响应的频谱特征、预测模型的特点、精度等方面总结了统计能量分析方法(SEA)在多个领域内的应用成果；聂旭涛等[3]利用稳态统计能量分析法对其包含机动抖振的随机振动环境进行预示，同时采用基于冲击响应谱的瞬态统计能量分析法预示导弹设备舱内的高频冲击环境；孙目等[4]针对某型号导弹的仪器舱进行了高频动力学环境预示，其仿真结果在300 Hz以上与试验值较好的吻合；伍先俊等[5]以简单潜艇模型为例，从振源排序，传递路径分析等方面，利用统计能量法对其应用技术进行了研究。

本文以X-43A为研究对象，基于统计能量分析的方法，建立其结构模型。为了重点研究飞行器噪声致振的性质和规律，本文假定飞行器外部噪声场已知，通过统计能量分析计算噪声传递与结构耦合振动，获得飞行器空腔结构在宽频外噪声场激励下的结构振动响应以及舱内的噪声场响应，并通过噪声试验验证理论与数值计算的可靠性。

1 飞行器结构声振耦合统计能量建模

1.1 飞行器结构模型

飞行器主体结构采用3 mm全等厚不锈钢板焊接，中部机舱下方开矩形窗，用于连接可拆卸的发动机机箱，发动机机箱可拆卸的目的在于可装卸机舱内声压、振动测量传感器；发动机机箱通过紧固螺栓与机舱连接，并过通过发动机机箱上面的密封橡胶圈使机舱内形成密闭空腔，并设计有噪声致振试验所需声传感器穿线孔。其结构示意图如图1所示。飞行器结构材料为不锈钢板(304)，其物理参数如下:密度ρ为7 800 kg/m3，弹性模量E为2.1×1011Pa，切变模量G为8×1010Pa，泊松比μ为0.3125。

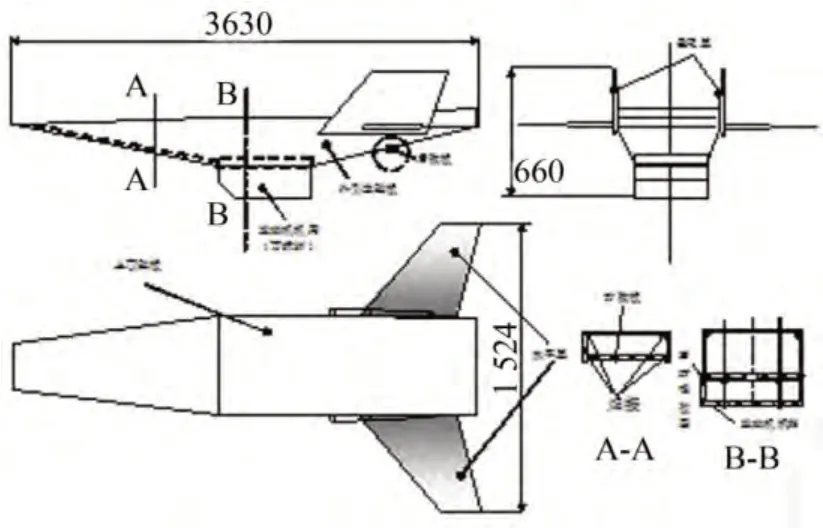
图1 飞行器结构示意图

1.2 飞行器结构统计结构模型

一般根据以下两个原则建立模型：一是确定结构振动的主要模态群，即对不同结构，总存在着主要的振动模态，在能量的传输、消耗和存贮中起主要作用；一是结构之间的连接方式，它决定了振动能量传输的大小[6]。根据文献[7]，建立X-43 A飞行器的有限元模型，并导入到Vaone软件中，SEA模型如图2所示。将其简化为内部中空的壳体结构飞行器，属于板—壳结构，外壳直接受外界噪声场激励，振动能量只有壳体—内部声腔传递路线，各个子系统间的能量传递如图3所示。

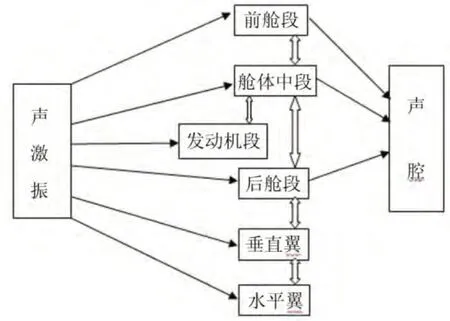
图3 能量流传递路径

根据统计能量法划分子结构的原理，结合自然几何形状、材料介质性质以及能量储存方式，将飞行器结构模型划分为前舱段，舱体中段，后舱段，发动机段，垂直机翼，水平机翼等20个结构子系统和一个声腔子系统，在能量传递的过程中，还有子系统本身的能量损耗，为了突出声激励能量传递到内声腔的路径，图中未标出各系统自身损耗的那部分能量。

2 统计能量分析参数确定及功率流平衡方程组建立

2.1 统计能量分析参数确定

统计能量法成功应用与否在一定程度上取决于准确获取各子系统的模态密度、内损耗因子和子系统间的耦合损耗因子等三个参数。

2.1.1 模态密度

统计能量分析中的模态密度n(f)定义为单位频率中的模态数目，对于由简单的子系统组合而成的结构，其模态密度近视可以认为是各个简单子系统的模态密度之和。

[1]给出了板的模态密度估算公式为

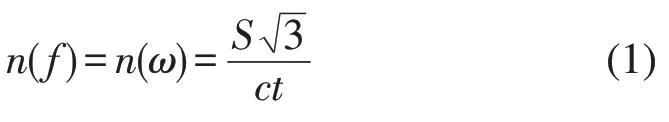
式中S为板面积；t为板厚；c=E ρ(1-μ2)为板内纵波速度。

三维声腔的模态密度估算公式为[8]

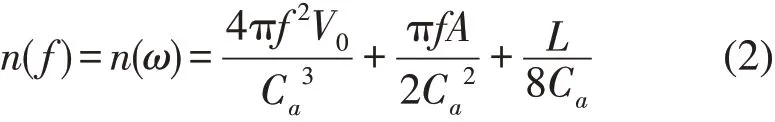
式中V0为声场的体积；A为声腔内表面积；L为声腔边线总长；Ca为声速。

2.1.2 内损耗因子

内损耗因子ηi是由三种彼此独立的阻尼机理构成的

式中ηis是结构子系统本身材料内摩擦构成的结构损耗因子；ηir是结构子系统振动声辐射阻尼形成的损耗因子；ηib是结构子系统边界连接阻尼构成的损耗因子。由于本文的模型子系统结构间是刚性连接，可以简化为：ηi=ηis+ηir。ηis由i结构的材料决定，参照文献[8]可得不锈钢的结构损耗因子ηis=5×10-4；公式ηir=ρ0cσir ωρs可以确定ηir，式中ρs、σir分别为子系统i的面积质量密度和辐射比。

由声场的混响时间TR求得声场的内损耗因子[9]

因此，得出声场的内损耗因子

式中S、V分别为声场空间的表面积和体积；c为声场的声速；α为声场围壁的吸声系数。

2.1.3 耦合损耗因子

耦合损耗因子ηij是两个耦合子系统i和j之间的链，即它确定两者之间的耦合程度。本文中，耦合损耗因子包括结构之间的耦合，如各舱体段子系统之间的耦合，和结构与声场之间的耦合，如壳体与声腔之间的耦合。

两结构之间线连接的耦合损耗因子[9]

式中cBi为第i块板弯曲波的波速；L为直线长度；ω为所研究频带的中心频率；Si为第j个子系统的表面面积；τij为子系统i到子系统j直线连接的波传播系数。

结构与声场之间的耦合损耗因子[9]

式中下标s、v分别代表结构与声腔；ρ0、ρs分别为声腔和结构的密度；σ为结构的声辐射系数；c为声速。

2.1.4 输入功率

输入功率来自外界激励，对于不同的实际问题有着不同的外界输入功率计算方法。本文中的输入功率来自试验数据，表1为外界输入载荷谱（只给出总声压级为140 dB时的试验数据，其它噪声强度下的试验数据都可以获得）。为验证统计能量分析方法计算结果的准确性，将该模型放置在70 m3高声强混响室内进行噪声试验，试验给出了识别外声场总声压级、1/3倍频程声谱，给出了振动测点均方根加速度及功率谱密度等。

2.2 功率流平衡方程组建立

飞行器SEA模型由21个子系统组成，在保守、弱耦合情况下，当系统受不相关稳态激励振动时，由系统的运动方程，通过模态法、波动法或格林函数，可得如下子系统i的功率流平衡方程[8]

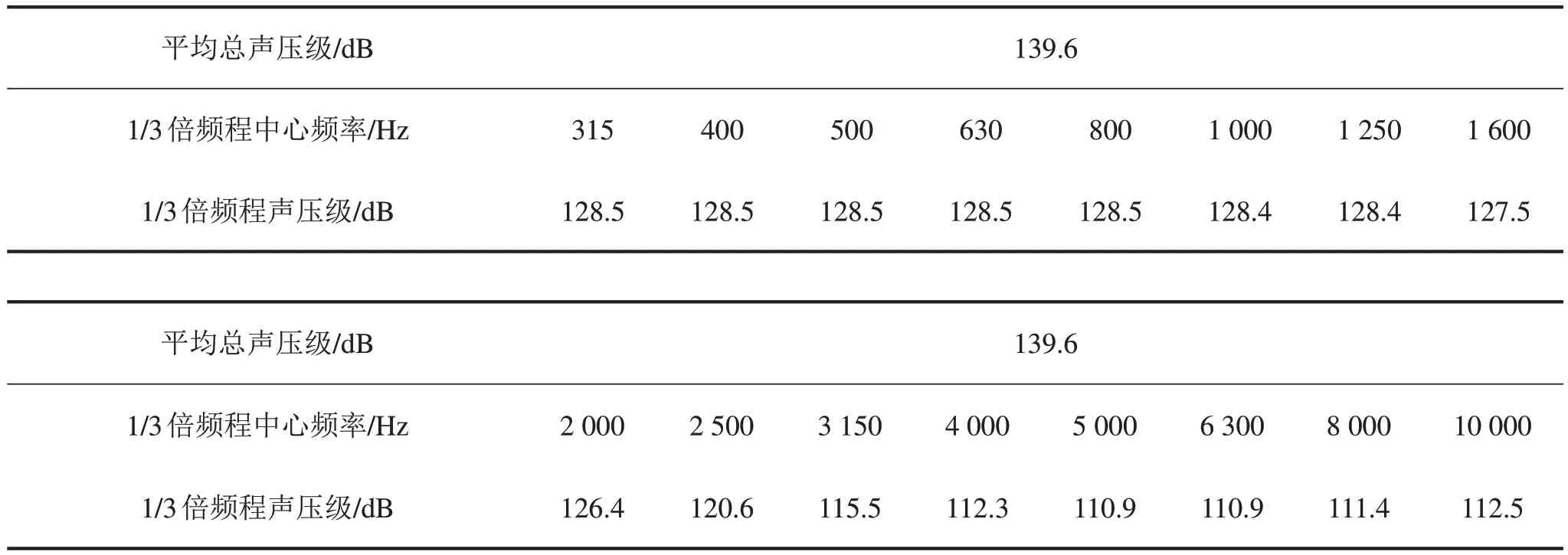
表1 施加在飞行器外表面的功率谱

式中Piin外界对为子系统i的输入功率；Pid为子系统i的损耗功率。

式(8)可写成如下形式

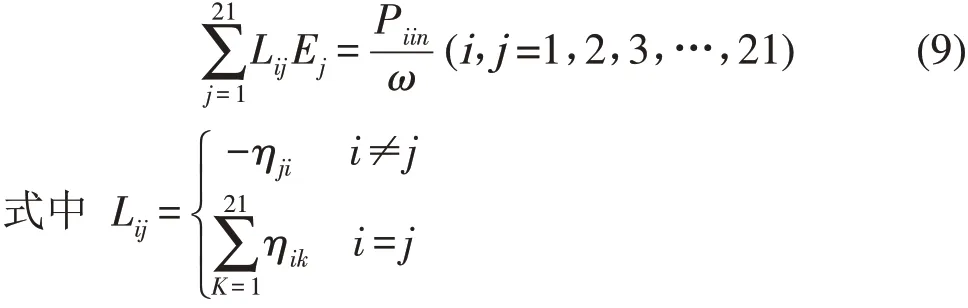
将互易原理关系式ni(ω)ηij=nj(ω)ηji代入式(9)，得统计能量分析关系式

其中ni(ω)为第i个子系统的模态密度。这样即可求得各子系统的振动能量。

3 统计能量计算与试验结果分析

进行结构模型声振耦合统计能量分析时，结构模型的力学边界条件取为自由边界条件，外部的噪声激励场采用均匀混响噪声，频率范围20～8 000 Hz，噪声强度140～160 dB。宽频噪声激振试验在高声强混响室完成，试验现场及吊装方式如图4所示。

3.1 结构舱内响应噪声声压计算与试验值对比

在三个激励噪声强度下，结构舱内的噪声响应计算声压值与试验结果对比如下图5—7。

图4 试验现场及吊装方式

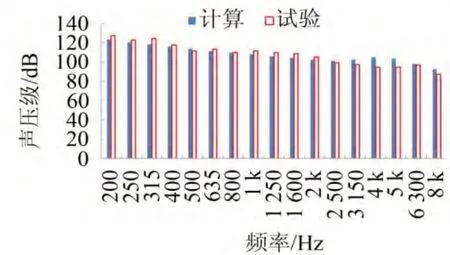
图5 仿真结果与试验值比较（140 dB）

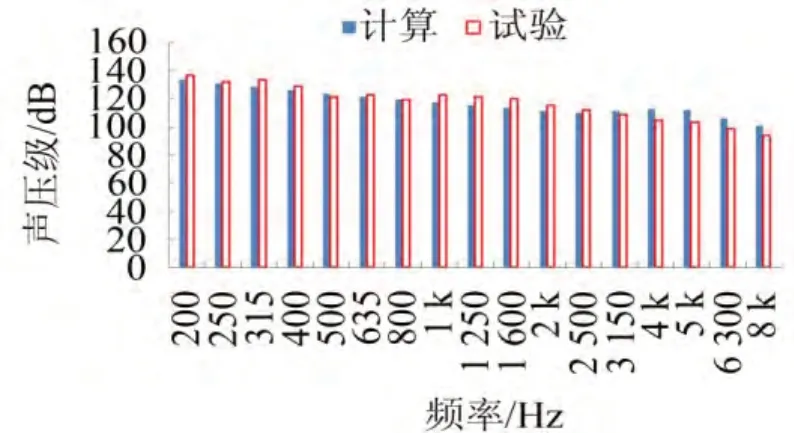
图6 仿真结果与试验值比较（150 dB）

图7 仿真结果与试验值比较（160 dB）

由图5—7可以看出：结构舱内响应噪声声压级计算值与试验测量值相比，不论在高频还是中低频，二者都较为一致，误差约3 dB，说明统计能量分析对噪声响应预测是比较可靠的。三个激励噪声强度下的结构舱内的噪声响应声压级的计算值与试验测量值还有一个共同的特点，就是在低频段，计算值小于试验值，在高频段，计算值大于试验值，而在中频段二者误差最小。舱内响应声压PSD在200～8 000 Hz范围内广泛分布，并且从低频到高频仅衰减大约20 dB。舱内响应声压值在4 000～5 000 Hz之间也有一个局部峰值，这类似于结构的振动响应加速度PSD的分布规律；舱内响应噪声强度至少低于激励噪声强度20 dB。这说明飞行器结构舱的封闭性较好。同时也表明结构与外声场的耦合较弱，因为有研究表明，在外声场与结构强耦合情况下，有可能舱内噪声大于舱外激励噪声。

3.2 结构子系统加速度功率谱密度（PSD）计算与试验值对比

飞行器SEA模型有20个结构子系统，后舱段底板子系统加速度功率谱密度计算值与试验值比较如图8所示。

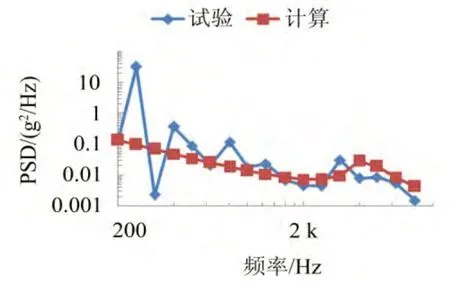
图8 仿真结果与试验值比较（140 dB）

图9 仿真结果与试验值比较（150 dB）

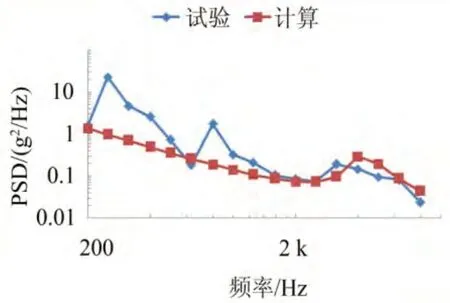
图10 仿真结果与试验值比较（160 dB）

由图8—10对比结果可以看出：结构声致振动响应的统计能量分析与试验结果趋势上较为一致，但低频段二者差异较大，高频段较为吻合。各子结构的结构振动响应加速度自谱(PSD)幅值总体上是随频率的增高而衰减，但在高频段(40 00～5 000 Hz)有一个明显的峰值，这是宽频噪声激励致使结构振动的重要特点，这也表明结构在高频段的响应是不容忽视的；各子结构的结构振动响应加速度自谱(PSD)幅值随激励噪声强度成比例增加，即激励噪声每增加10 dB，结构振动响应加速度自谱幅值就增加10倍。

4 结语

本文以X-43A为研究对象，按照SEA的基本思想，将飞行器划分为21个子系统，把各子系统之间作为保守耦合的假设下，建立了飞行器的SEA模型；假定飞行器外部噪声场已知，从而确定了系统的输入功率；采用理论、经验公式及试验数据确定了SEA模型的其它参数。通过仿真计算和试验相对比，数值模拟计算的典型结构舱内声压值和结构振动响应值与试验测量值误差不大于3 dB。计算表明统计能量法是一个可信的研究方法，是目前解决高频动力学问题的较好方法，能成功地应用到飞行器混合声场问题的分析，为进一步准确预示我国自行研发的飞行器仪器设备振动噪声环境奠定基础。

参考文献：

[1]王 昆.飞行器结构统计能量建模方法及声振响应分析研究[D].哈尔滨：哈尔滨工业大学航天学院，2010，7.

[2]刘海生，杨春庄，陈士杰.统计能量分析方法声振预测应用研究[J].声学技术，2010，29(2)：192-197.

[3]聂旭涛，熊飞峤.运用统计能量分析法预示空空导弹舱内动力学环境[J].振动与冲击，2007，26(4)：140-143.

[4]孙 目，王小军，潘忠文，等.统计能量分析在飞行器动力学环境预示中的应用[J].导弹与航天运载技术，2009，301(3)：11-14.

[5]伍先俊，朱石坚.统计能量软件Auto SEA应用技术研究[J].噪声与振动控制，2007，(5)：87-89.

[6]王宪成，张 晶，张更云.基于统计能量分析法的船艇机舱噪声建模计算[J].兵工学报，2007，28(11)：1367-1372.

[7]Laurie A,Marshall Griffin P.Corpening a chief engineer's view of the NASA X-43A scramjet flighttest[C].AIAA/CIRA 13 th International Space Planes and Hypersonics Systems and Technologies,AIAA,2005-3332.

[8]姚德源，王其政.统计能量分析原理及其应用[M].北京：北京理工大学出版社，1995.

[9]程广利，朱石坚，伍先俊.统计能量分析法及其损耗因子确定方法综述[J].船舶工程，2004，26(4)：10-15.