柔性转子滚动轴承系统混沌行为研究

崔 立 郑建荣

1.上海第二工业大学，上海，201209 2.华东理工大学，上海，200237

0 引言

滚动轴承支承的转子系统由于轴承非线性刚度而出现复杂的非线性动力学特性。近年来，刚性转子滚动轴承系统的分叉及混沌特性研究得到了广泛的重视。

Jang等［1］考虑滚动轴承的5个自由度以及表面波纹度建立了刚性转子滚动轴承系统的非线性动力学方程，发现套圈的波纹会导致径向位移和角位移响应峰值附近出现边频带。Harsha［2－3］考虑轴承间隙、不平衡力研究了转子系统的动力学响应，发现系统的动力学行为与滚动体的通过频率有关，且当通过频率及其谐波与固有频率相等、外圈波纹度阶数与滚动体数目相等时振动幅值将变得极大。Bai等［4］研究了主轴－滚动轴承系统非线性动力学行为，发现轴承间隙的减小有利于提高主轴轴承系统的稳定性。高尚晗等［5］研究了主轴－滚动轴承在负游隙情况下的机床主轴－滚动轴承系统的非线性动力学特性，揭示了主轴系统的混沌演化过程。崔立等［6］研究了圆柱滚子轴承刚性转子系统周期运动分岔特性，发现随着径向间隙、阻尼和力矩的变化，周期运动将产生倍周期或Hopf分岔，分岔转速随参数变化而改变。

以上的研究对象均为刚性转子，模型涉及转轴的弯曲变形和陀螺力矩等参数。随着旋转机械转速的提高，柔性转子系统的设计与分析变得越来越重要。近年也有一些研究柔性转子轴承系统的文章发表，如：Laha等［7］研究了油膜轴承支承的柔性转子系统的分叉行为，分析了转轴的材料、刚度和质量等参数对转子系统分叉行为的影响。Villa等［8］、Sinou［9］研究了球轴承支承的柔性转子系统的非线性动力学行为，发现系统响应中存在跳跃现象和超谐波，但其研究仅考虑了4个自由度的转轴节点和2个轴承自由度，难以满足实际工况的需求。

本文采用12自由度Euler－Bernoulli杆单元建立柔性转子滚子轴承系统的非线性动力学模型，研究系统的混沌行为，分析轴承结构参数与转轴结构参数对转子系统混沌行为的影响规律。

1 计算模型

图1所示为柔性转子轴承系统模型，采用12自由度的Euler－Bernoulli杆单元，圆盘简化为质点并考虑其质量与转动惯量，转子由两个滚动轴承支承。

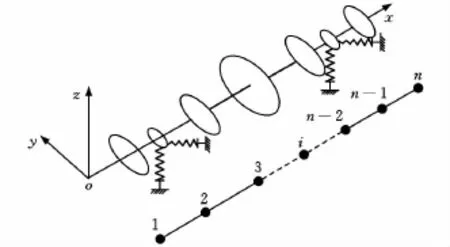
图1 柔性转子滚动轴承系统模型

1.1 柔性转子轴承系统动力学模型

柔性转子系统的动力学方程为

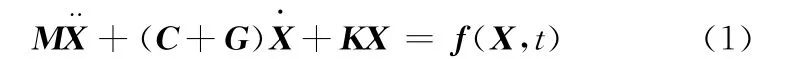
式中，M为包含转轴、圆盘和轴承的总质量矩阵；C为总阻尼矩阵；G为总陀螺矩阵；K为总刚度矩阵；X为转子各节点的位移向量；f（X，t）为包括转子各节点轴承力、重力、转子不平衡力和外载荷的矩阵。

先对转子系统进行轴段与节点划分，然后进行转子系统的质量矩阵、刚度矩阵、阻尼矩阵、陀螺矩阵、载荷矩阵求解，并按照节点的顺序对各矩阵进行组装，具体过程如下：首先计算杆单元的质量矩阵、陀螺矩阵、刚度矩阵、载荷矩阵并组装；然后将刚性圆盘的质量矩阵、陀螺矩阵、不平衡力矩阵叠加到所在节点的相应矩阵中；之后将支承轴承的质量矩阵、非线性轴承力叠加到所在节点的相应矩阵中；最后计算系统的结构阻尼、轴承阻尼矩阵并组装。

1.2 杆单元

图2所示为针对空间杆单元分析获得的空间杆单元两端节点位移。

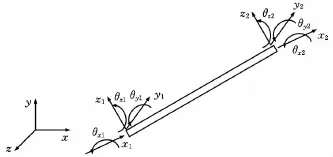
图2 二节点空间杆单元

针对图2中12自由度Euler－Bernoulli杆单元，若每个节点考虑6个自由度，则共有6个广义位移和6个广义力，其表达式为

式中，xi、yi、zi分别为节点i沿x、y、z方向的线位移；θxi、θyi、θzi分别为节点i处截面绕x、y、z轴的转角位移；Fxi、Fyi、Fzi分别为节点i在x、y、z方向受到的轴向力和剪切力；Mxi、Myi、Mzi分别为节点i在x、y、z方向所受的扭矩和弯矩。

假设已知杆单元横截面面积、截面惯性矩、单元的扭转惯性矩、长度、材料弹性模量和剪切模量，则可根据有限元理论［10］求出杆单元的质量矩阵Ms、刚度矩阵Ks、阻尼矩阵Cs、陀螺矩阵Gs。

1.3 刚性圆盘模型

当轴上安装有圆盘时，将其视为刚性圆盘，并将其质量矩阵、陀螺矩阵、不平衡力矩阵叠加到所在节点的相应矩阵中。

假设已知圆盘的质量、半径、不平衡质径积，则可建立刚性圆盘的质量矩阵Md、陀螺矩阵Gd、不平衡力矩阵Fd，其中Fd为

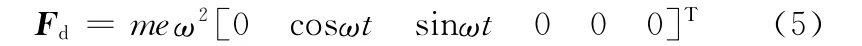
式中，me为圆盘的不平衡质径积；ω为转速。

1.4 滚子轴承模型

考虑普遍受载的圆柱滚子轴承，其模型如图3所示，图中，Dr为滚子直径，D1、D2分别为外圈外径和内圈内径，δ0为径向间隙，le为带凸度滚子的长度，ls为带凸度滚子直线部分的长度。

假设滚子数目为N，使用切片法将滚子分成nr个圆片。对第j个滚子进行受力分析，假设第j个滚子方位角为φj，根据赫兹接触理论，并使用拟动力学方法建立滚子轴承的非线性平衡方程组，使用Newton－Raphson法可求出滚子与套圈的接触力［11］。将各滚子的接触力分解，即可求出圆柱滚子轴承的非线性轴承力矩阵：

图3 圆柱滚子轴承结构简图

式中，F2jk为第j个滚子的第k个切片与滚子轴承内圈的作用力。

1.5 结构阻尼求解

Rayleigh提出的结构阻尼模型计算表达式为

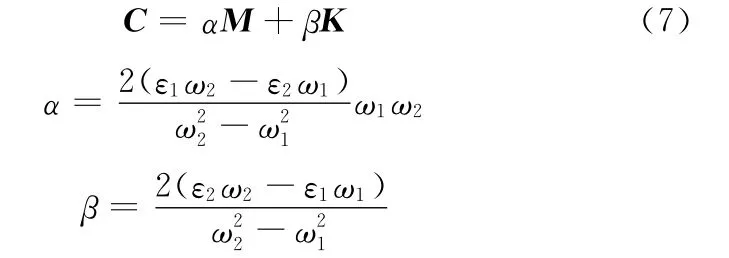
式中，ε1、ε2为两个振型的阻尼比，根据经验取ε1＝0.005，ε2＝0.01；ω1、ω2为转子系统的二阶固有频率。

式（7）中转子系统的固有频率ω1、ω2可根据计算得到的质量矩阵、刚度矩阵解｜K－Mω2｜＝0得到。

2 计算方法

采用Runge－Kutta法、Newton－Raphson法进行非线性动力学方程组求解，根据FPA修正法确定求解周期，然后求解最大Lyapunov指数，判断系统的动力学行为。

2.1 求解周期的确定

转子轴承系统中存在轴承变刚度激励，还可能存在不平衡力激励。不平衡力产生的激励周期为轴转动周期的整数倍，但轴承的变刚度激励周期往往不是轴转动周期的整数倍，所以在判断和求解时，采用修正的FPA法建立统一的求解周期［12］，其表达式定义为

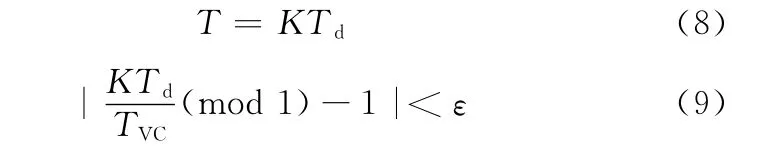
式中，T为求解周期；Td为不平衡力激励周期；TVC为轴承变刚度激励周期；ε为常数，取ε＝0.01；K为比例系数，K ＝1，2，…，nk。

根据式（9）进行循环计算，直至找到满足其要求的K值，代入式（8）即得求解周期。

2.2 Lyapunov指数计算

Lyapunov指数表示在相平面中2条相邻轨线间的距离随时间的平均指数发散率，它明确地区分了确定性运动和混沌运动［13］。

对于连续系统有

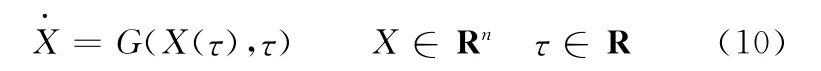
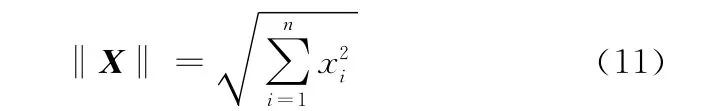
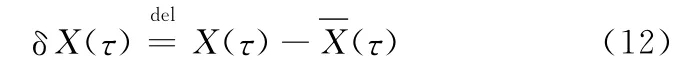
设在τ0时刻‖δX（τ0）‖充分小，于是1维的Lyapunov指数可定义为

在n维连续系统中，δX（τ）在每个基底上有分量，每一个分量均可按上式求出一个λ，因此共存在n个Lyapunov指数λi，称为Lyapunov指数谱。当任意选取矩阵δX（τ）时，Lyapunov指数以概率1可能取得最大值，如果其中最大的Lyapunov指数λmax＞0，则该系统一定存在混沌运动。因此，只要计算出系统的最大Lyapunov指数，就可以判断系统是否处于混沌状态。

3 计算与分析

图4为柔性转子系统简图，转轴由两个型号相同的滚子轴承支承，转轴中有刚性圆盘，该圆盘可施加不平衡力。

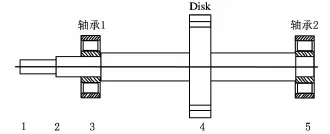
图4 柔性转子系统简图

表1所示为滚子轴承的结构参数，其中，轴承的弹性模量为204GPa，泊松比为0.3，阻尼为200N·s／m，轴承载荷为｛0，2000N，2000N，0，0｝。

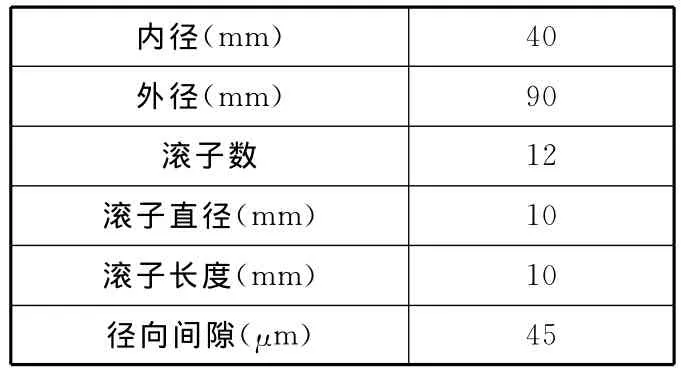
表1 滚子轴承的结构参数

柔性转子系统的结构参数如表2所示，转轴被划分为4个轴段，转子系统划分为5个节点。转轴的弹性模量为204GPa，泊松比为0.3。

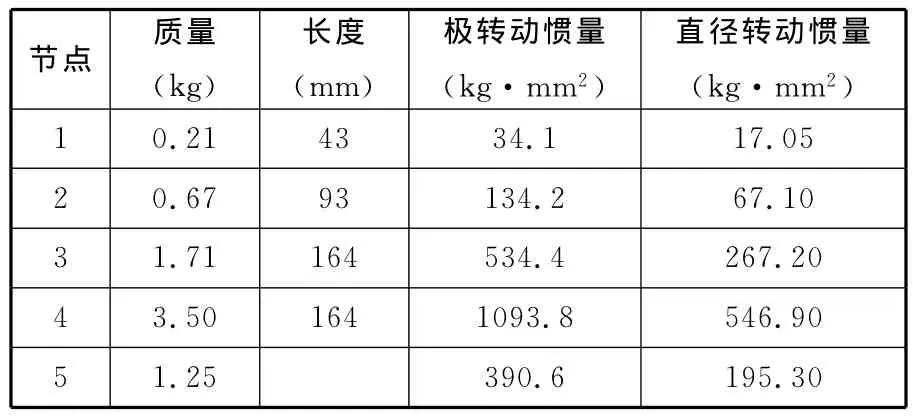
表2 柔性转子系统结构参数

对图4所示的柔性转子系统进行计算，判断圆盘节点处的混沌行为，并分析轴承径向间隙、圆盘不平衡力、转轴刚度比等参数对系统混沌行为的影响规律。

3.1 径向间隙影响分析

假设系统不平衡力为0，则轴承径向间隙对系统混沌特性的影响如图5所示。分别取40μm、60μm和80μm的径向间隙计算系统的最大Lyapunov指数。

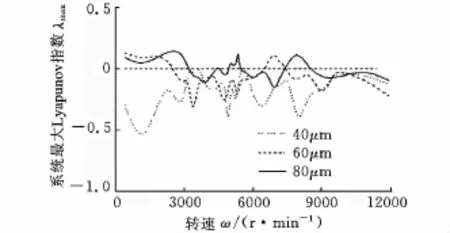
图5 不同节点处的最大Lyapunov指数

系统最大Lyapunov指数小于0，表明系统运动是稳定的；当最大Lyapunov指数等于0时，系统为倍周期或拟周期分叉运动；当最大Lyapunov指数大于0时，系统为混沌运动。

为了验证计算的准确性，使用Runge－Kutta法进行非线性动力学方程组求解，得到转子系统响应的频谱图和Poincaré截面。从图5可知，当径向间隙为80μm、转速为4200r／min时，系统的最大Lyapunov指数等于0（图中fVC为滚子轴承的变刚度振动频率）。图6所示为图5工况下圆盘节点处的频谱图和Poincaré截面，图形表明系统为拟周期振动。

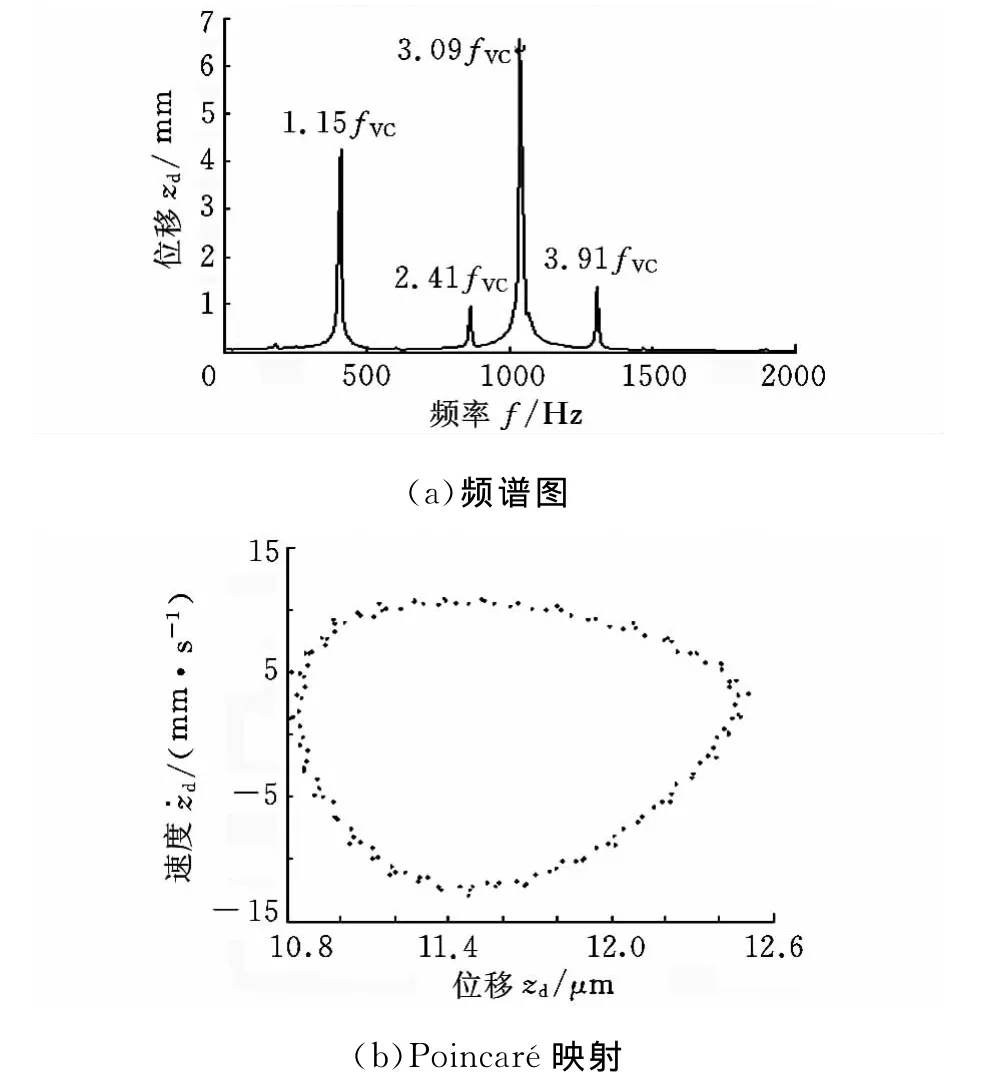
图6 转速为4200r／min、径向间隙为80μm时的响应

图5表明，径向间隙为80μm、转速为8000 r／min时，系统的最大Lyapunov指数大于0，图7所示为对应该工况的圆盘节点处的频谱图和Poincaré截面，其表明系统为混沌运动。

图5还表明，当径向间隙为40μm时，系统的最大Lyapunov指数小于0，未出现混沌行为；当径向间隙为60μm 时，在0～2500r／min、6600～7200r／min转速下的最大Lyapunov指数大于0，系统出现混沌行为；当径向间隙为80μm时，在0～3100r／min、5000～5400r／min、7500～8500 r／min转速下出现混沌行为。

3.2 不平衡力影响分析

图8所示为在其他条件不变前提下的不平衡力对系统混沌特性的影响。分别取圆盘的不平衡质径积为5×10－6kg·m、1×10－5kg·m、2×10－5kg·m，计算系统的最大Lyapunov指数。

从图8可知，当不平衡质径积为5×10－6kg·m时，在0～2000r／min，系统出现混沌行为；当不平衡质径积为1×10－5kg·m时，在0～3700r／min，系统出现混沌行为；当不平衡质径积为2×10－5kg·m时，在0～4400r／min，系统出现混沌行为。可以看出，不平衡力的存在会改变系统的混沌行为，系统出现混沌的转速及范围随着不平衡力的增大逐渐增大。

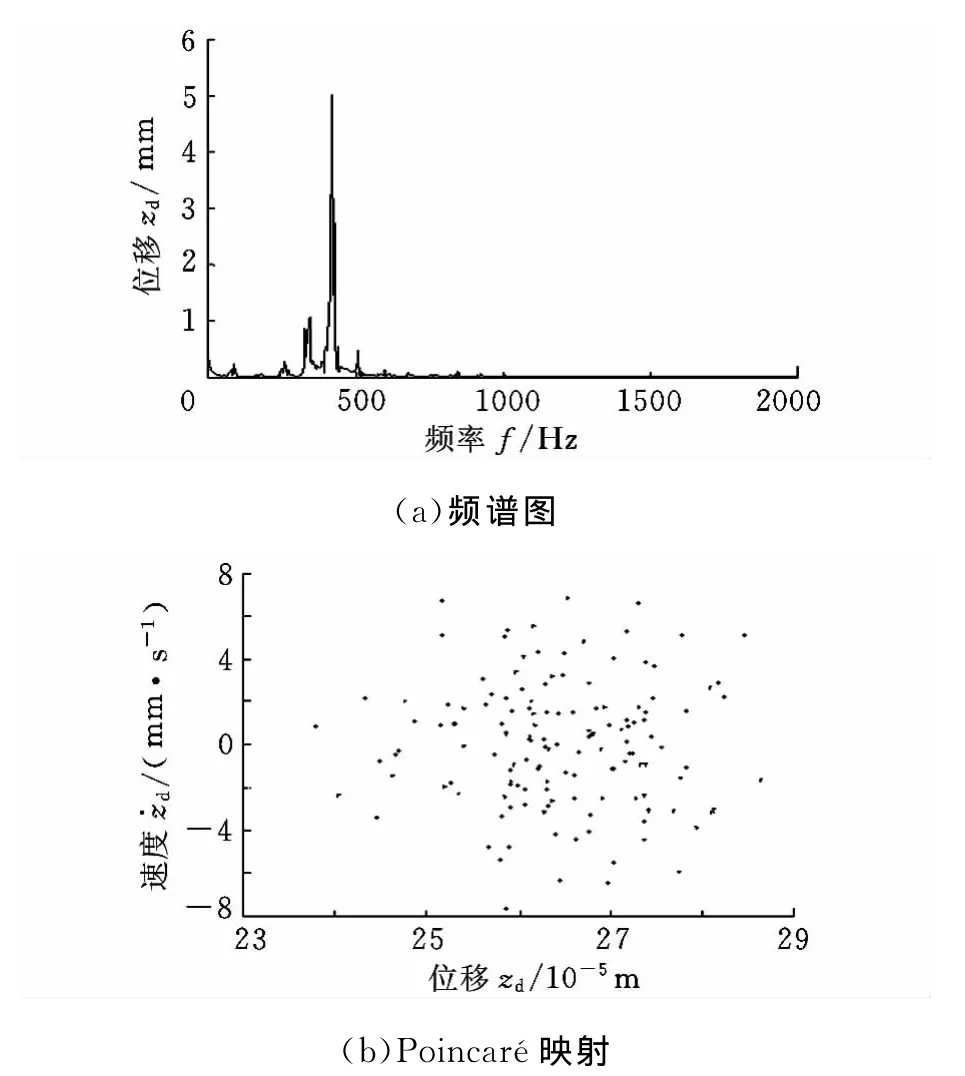
图7 转速为8000r／min、径向间隙为80μm时的响应

图8 不同不平衡力时的系统最大Lyapunov指数

3.3 刚度比影响分析

定义柔性转子系统的刚度比为

式中，Kshaft为柔性转轴的刚度；Kbearing为支承轴承刚度。

在其他参数不变的情况下，分别取长度为500mm、400mm、300mm的转轴进行刚度比计算，其对应所得的刚度比分别为7.38×10－3、1.43×10－2、3.31×10－2，据此，可得出刚度对于柔性转子系统动力学特性的影响。

图9所示为不同刚度比时圆盘节点处的振幅随转速变化曲线，可以看出，随着刚度比的增大，振幅峰值对应的转速逐渐增大，即临界转速增大；振幅峰值也随着刚度比增大而增大，且临界转速附近的峰值逐渐变多，可以看出随着转轴刚度增大，轴承非线性振动对转子系统的影响增大，导致系统响应复杂。

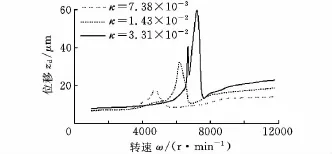
图9 不同刚度比时的圆盘节点振幅

图10所示为不同刚度比时最大Lyapunov指数随转速的变化曲线。当刚度比为7.38×10－3时，在0～800r／min出现混沌行为。当刚度比为1.43×10－2时，在0～1200r／min、5200～5400r／min出现混沌行为。当刚度比为3.31×10－2时，在0～3200r／min、4800～5900r／min出现混沌行为。

图10 不同转轴刚度比时的系统最大Lyapunov指数

可见，随着转轴刚度增大即刚度比增大，混沌运动的区间发生改变。随着刚度比的增大，系统的混沌区间增大，轴承引起的转子系统非线性行为明显。对比柔性转子和刚性转子的混沌特性，发现轴承的非线性接触力对刚性转子系统的混沌特性影响大于柔性转子。

4 实验

为验证本文方法对柔性转子系统动力学行为预测的准确性，使用图11所示的高速滚子轴承柔性转子实验器进行测试。动力装置的高速电主轴，最高转速可达24 000r／min，实验滚子轴承参数如表1所示，实验过程中滚子轴承承受的径向载荷为2000N。采用非接触式的电涡流传感器测量滚子轴承及圆盘处的径向振动位移。

图12所示为转子圆盘处振动位移幅值计算结果与实验结果对比，可以看出，计算得到的一阶临界转速为4900r／min，实验得到的一阶临界转速为4700r／min，与计算结果较为接近；实验测试振幅与计算结果也较为接近，证明了本文方法的准确性。

图11 滚动轴承转子系统实验器

图12 幅值计算结果与实验结果对比

5 结论

（1）轴承径向间隙是影响转子系统非线性振动特性的重要参数。随着轴承径向间隙的增大，系统的混沌区间逐渐增大、变多。

（2）不平衡力的存在对系统混沌行为也有较大的影响。系统出现混沌的转速及范围随着不平衡力的增大逐渐增大。

（3）随着转轴刚度比增大，转子振幅峰值以及对应的转速均逐渐增大。共振转速附近产生混沌运动对应的转速增大时，系统混沌区间也增多，轴承非线性对系统响应影响明显。

［1］Jang G H，Jeong S W.Nonlinear Excitation Model of Ball Bearing Waviness in a Rigid Rotor Supported by Two or More Ball Bearings Considering Five Degrees of Freedom［J］.Transactions of the ASME，2002，124：82－90.

［2］Harsha S P.Non－linear Dynamic Analysis of an Unbalanced Rotor Supported by Roller Bearing［J］.Chaos，Solitons and Fractals，2005，26：47－66.

［3］Harsha S P.Non－linear Dynamic Response of a Balanced Rotor Supported by Rolling Element Bearings Due to Radial Internal Clearance Effect［J］.Mechanism and Machine Theory，2006，41：688－706.

［4］Bai Changqing，Xu Qingyu.Dynamic Model of Ball Bearings with Internal Clearance and Waviness［J］.Journal of Sound and Vibration，2006，294：23－48.

［5］高尚晗，龙新华，孟光.主轴－滚动轴承系统三种分岔形式［J］.振动与冲击，2009，28（4）：59－64.Gao Shanghan，Long Xinhua，Meng Guang.Three Bifurcation Types in the Spindle－ball Bearing System［J］.Journal of Vibration and Shock，2009，28（4）：59－64.

［6］崔立，刘长利，郑建荣.圆柱滚子轴承刚性转子系统周期运动分岔研究［J］.振动、测试与诊断，2011，31（5）：637－641.Cui Li，Liu Changli，Zheng Jianrong.Periodic Motion Bifurcation of Rigid Rotor System in Cylinder Roller Bearing［J］.Journal of Vibration，Measurement ＆ Diagnosis，2011，31（5）：637－641.

［7］Laha S K，Kakoty S K.Non－linear Dynamic Analysis of a Flexible Rotor Supported on Porous Oil Journal Bearings［J］.Communications in Nonlinear Science and Numerical Simulation，2011，16：1617－1631.

［8］Villa C，Sinou J J，Thouverez F.Stability and Vibration Analysis of a Complex Flexible Rotor Bearing System［J］.Communications in Non－linear Science and Numerical Simulation，2008，13：804－821.

［9］Sinou J J.Non－linear Dynamics and Contacts of an Unbalanced Flexible Rotor Supported on Ball Bearings［J］.Mechanism and Machine Theory，2009，44：1713－1732.

［10］Wang Maocheng.Finite Element Method［M］.Beijing：Tsinghua University Press，2008.

［11］Harris T A.Rolling Bearing Analysis［M］.New York，USA：John Wiley ＆Sons，2001.

［12］Choi S K，Noah S T.Response and Stability Analysis of Piecewise Linear Oscillations under Multi－forcing Frequencies［J］.Nonlinear Dynamics，1992，3：105－121

［13］Wolf A，Swift J B，Swinney H L.Determining Lyapunov Exponents from a Time Series［J］.Physica D.，1985，16：285－317.