双横臂悬架硬点位置的设计优化及运动学仿真

龚国彬，魏忠宣，张 敏，胡久强

Gong Guobin1，Wei Zhongxuan2，Zhang Min2，Hu Jiuqiang2

（1.重庆车辆检测研究院有限公司 国家客车检测中心，重庆 401122；2.上汽依维柯红岩商用车有限公司，重庆 401122；）

0 引 言

1 双横臂独立悬架硬点设计

双横臂独立悬架硬点位置的设计匹配应满足：在悬架运动时，车轮定位参数变化范围要小，变化趋势要合理；在制动时，悬架应使车辆具有一定的抗“点头”效果。为此针对某车型，根据整车参数和布置要求，进行硬点的设计匹配和优化，设计所需输入参数如表 1所示，双横臂悬架结构示意如图1所示。

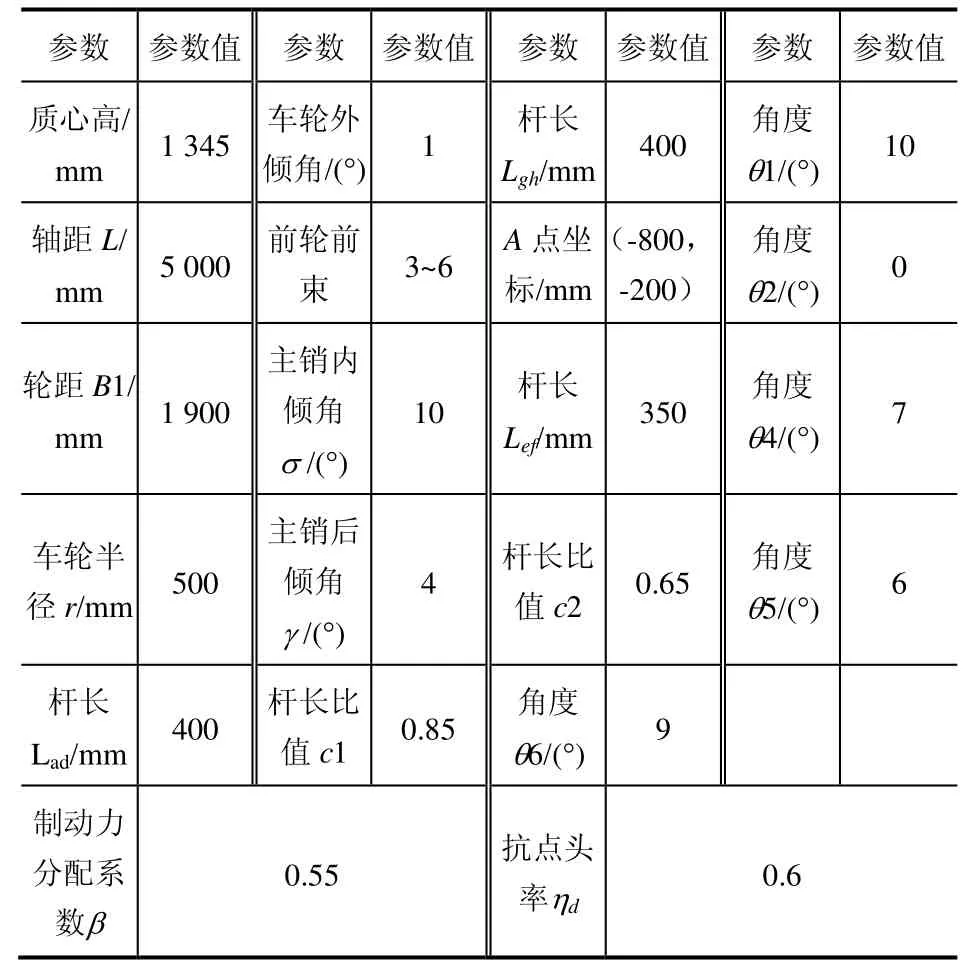
表1 双横臂悬架设计参数

1.1 横向平面匹配计算

在横向平面内，为了获得理想的悬架特性和力矩中心位置，悬架导向机构一般选择图 2所示布置方案。同时，在悬架上下运动时，希望轮距变化要小，车轮定位参数变化范围要小，且变化趋势要合理，所以上、下摆臂的杆长比范围为0.6～1.0，文中杆长比取0.65为宜，设计计算过程和方法如下。

根据悬架的空间布置要求，可以初步确定下摆臂A点坐标为（-800，-200），以及杆长Lad=400，进而根据主销内倾角σ、杆长比 c1、c2和轮距等设计参数可确定如下坐标：

在导向机构横向平面内，可根据上、下摆臂的布置方案来计算侧倾中心位置。根据表 1中的设计参数和悬架硬点投影几何关系，计算如下：

同理，可以得到C、D、M点的坐标。

1.2 纵向平面匹配计算

在纵向平面内，导向机构的投影如图 3所示。为了提高汽车的行驶平顺性和制动稳定性，期望主销后倾角在悬架压缩行程增大，在拉伸行程减小，用以在制动时产生一定的抗前俯力矩。同时，为了使悬架具有一定的抗“点头”效果，上摆轴EF应向后倾斜一定的角度，使纵倾中心位于前后轴之间。

兴延高速公路是2022年北京冬奥会的配套工程，南起西北六环路双横立交，途经昌平区，北至延庆区京藏高速营城子立交收费站以北，全长约42.2公里。大兴国际机场即北京新机场，建成后将是世界最大空港，成为展现我国国家形象的新国门。

式（9）表示汽车抗前俯率ηd，其中L为轴距；h为质心高度；β为制动力分配系数。当这几个参数已知时，即可通过式（9）求得图3所示角度φ。另外，通过初选上摆轴的定位角θ4，利用式（12）即可求得纵向瞬时中心Io的位置，由此可求得由纵倾中心确定的下摆轴定位角θ3，如式（13）所示。

再根据表 1的设计参数和悬架硬点投影几何关系，求出E、F、G、H各点的坐标值如下：

1.3 水平面匹配计算

导向机构在水平面内的投影，如图4所示，在水平面内，选择布置方案时，要兼顾考虑上、下横臂在纵向平面内的布置情况。为了减小主销后倾角的变化，使摆臂轴线夹角θ5＜θ6，且都为正。根据表 1设计参数和投影几何关系可计算出其他硬点坐标值，因E、F、G、H各点的x和z坐标值已经求出，在此只需计算y坐标即可，计算如下：

表2 双横臂导向机构硬点匹配计算结果

通过对双横臂导向机构在 3个投影面的分析匹配计算，汇总匹配计算结果如表2所示。

2 双横臂独立悬架硬点优化

双横臂独立悬架硬点匹配设计结果不一定是最优的，在此利用Adams/Insight模块对设计结果进行优化。在实施优化前，需根据仿真结果和设计经验，找出具有较高灵敏度的设计参数作为设计变量，这样可利用缩减设计优化空间，达到快速有效的优化效果。

2.1 应用Insight模块进行优化

在Adams/Insight模块中，选择车轮前束角和主销内倾角2个参数为优化目标。选择悬架B、E、F、G、H 5个硬点位置共11个坐标参数为设计变量，并设定相应的取值范围进行优化设计计算。在仿真计算结束后，调用Adams/Car菜单Simulate下的DOE Interface→Design Objective→New，创建优化目标，然后选择 DOE Interface→Adams/Insight→Export导出到 Adams/Insight，并进入Adams/Insight界面。选择二水平试验方法，设定变量因素及响应，创建工作矩阵，最后进行迭代计算。

2.2 优化结果分析

根据优化目标调整相应的设计变量，进行多目标优化，硬点坐标优化结果如表 3所示。利用优化结果作原始参数，输入所建立的运动学模型进行仿真和对比，分析结果如图5～图8所示（b01为优化前，c01为优化后）。从优化前、后仿真结果分析可知，优化后车轮前束角、车轮外倾角、主销后倾角、主销内倾角 4个车轮定位参数值的变化范围明显减小，变化规律得到明显改善，可知所进行的优化是可行和有效的。

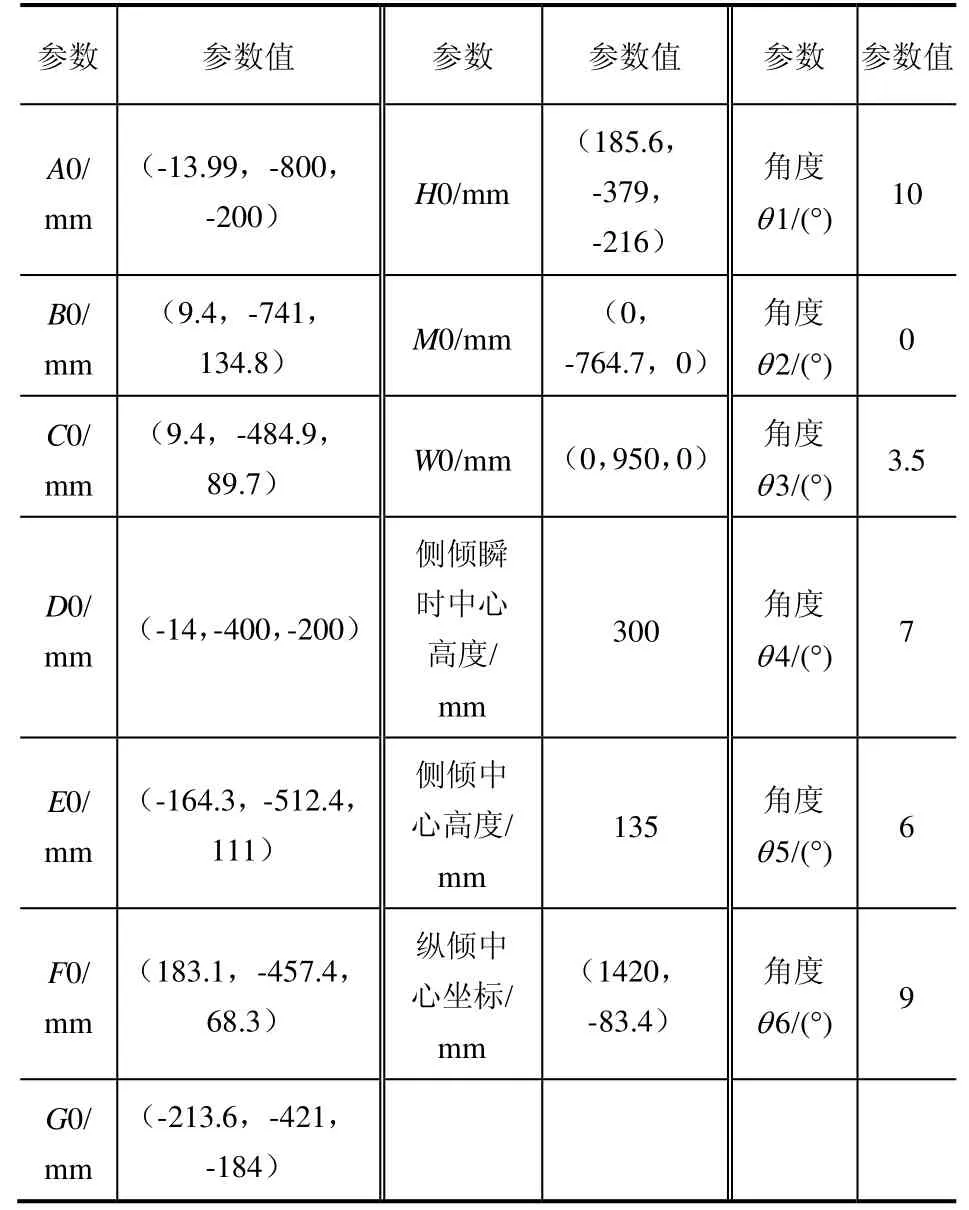
表3 双横臂导向机构硬点优化结果

3 双横臂空间机构学运动学仿真

双横臂独立悬架是一种比较复杂的 RSSR机构，基于多体系统动力学、空间机构学，并结合相应的数学方法和优化算法，建立了相应的数学模型，通过Matlab编程实现了悬架运动学仿真。图 9所示为双横臂独立悬架的空间拓扑结构，各点的初始值由前述的结构设计和优化所得，汇总如表4所示。

1）计算各杆件长度等初始值

利用两点间距离公式计算各杆件长度，如Ldf，Lef，Lcf，Lmn，Lfn，Lcn等初值。

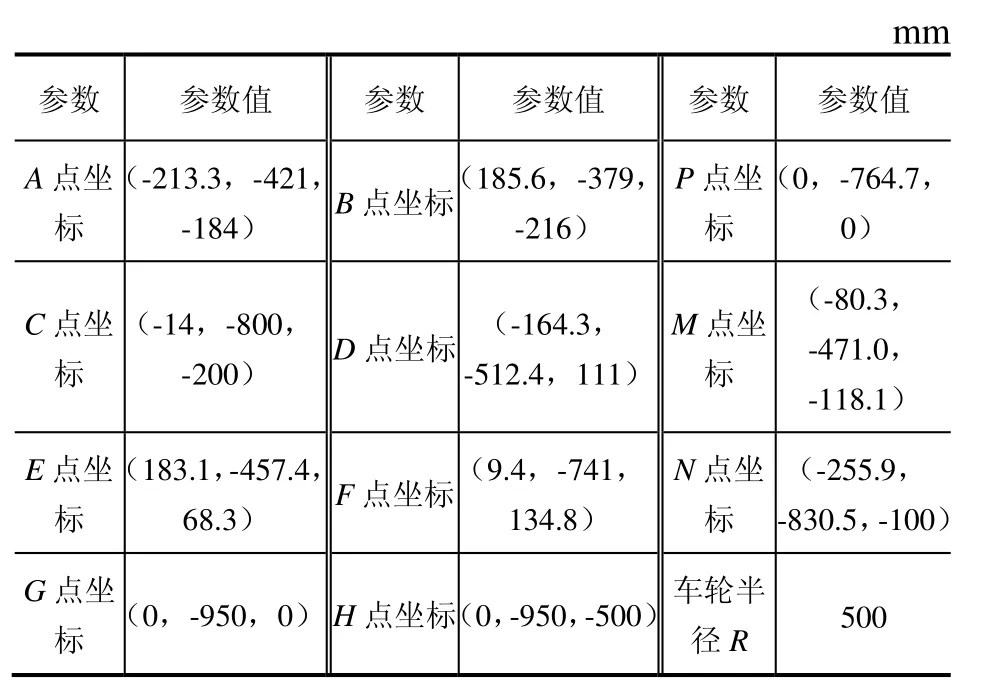
表4 双横臂悬架结构硬点坐标值

2）计算Cφ点位置

C点绕轴AB旋转角度φ后的位置坐标Cφ为

其中，Cφ为C点旋转后在全局坐标系中的值；为局部坐标系原点O1在全局坐标系O中的坐标向量；(rc)o1为C点在局部坐标系O1中的局部坐标向量；为C点绕轴AB旋转的变换矩阵；cos∂,cosβ,cosγ为轴 AB在全局坐标系中的方向余弦。

3）上摆臂转动角度及Fω点的计算求解

下摆臂的运动必然导致上摆臂DE也转动一个角度ω，从而引起F点位置变换，在此可以用类似求C点的方法进行求解，参数含义参照C点计算公式。

自此 Cφ和Fω都已用数学表达进行，但是 Fω中的ω为未知数。由于杆长CF不变，故可列出如下方程进行求解。

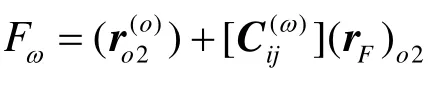
4）P点新坐标计算

根据杆长比和Cφ、Fω点坐标值，可计算出P点在全局坐标系中的坐标值

5）N点和G点坐标计算

在运动中，N点到F、M、C 3个点的距离始终不变，故可联立方程组进行求解，该方程组为三元二次非线性方程组，需要引用非线性优化的方法进行求解。G点与N点的求解方法相同，在此不再详述。

6）车轮接地点H坐标计算

当G点、P点和车轮半径R已知时，可利用几何关系求得车轮接地点H的坐标值。

7）计算车轮定位参数

4 硬点计算及运动学仿真的程序实现

双横臂独立悬架硬点位置的设计匹配较为复杂和繁琐，描述其运动规律有相当难度，计算工作量较大。通过以上分析和计算，使用Matlab编程实现了硬点的匹配计算和悬架运动学分析，所开发的计算软件界面如图10所示。通过该计算程序基本解决了双横臂导向机构的设计问题，提高了设计计算效率。

5 结束语

综上所述，以某车型为例，根据整车参数和布置要求，对双横臂独立悬架的硬点进行了匹配设计，并利用Matlab编写了相应的计算软件，从而形成了一套简单有效的双横臂硬点匹配设计方法和流程，基本解决了双横臂导向机构的设计问题，该方法具有一定的普遍适用性，在工程上具有一定的参考应用价值。

[1]张洪欣.汽车设计[M].北京：机械工业出版社，1998.

[2]韩建友.高等机构学[M].北京：机械工业出版社，2004.7.

[3]余志生.汽车理论[M].北京：机械工业出版社，2002.

[4]高翔，李江，程建平.双横臂独立悬架导向机构运动学分析及优化[J].拖拉机与农用运输车，2008（1）：46-48.

[5]龙岩.双横臂悬架专家系统导向机构知识体系的建立[D].长春：吉林大学，2008.

[6]廖抒华，段守焱，王金波.Adams/Car与Insight在汽车前悬架仿真与优化中的联合应用[J].机械设计与制造，2010（10）：137-139.北京汽车