区间线性规划最优解对应的约束矩阵的构造

(杭州电子科技大学理学院，浙江 杭州310018)

0 引 言

对于不确定性规划，人们一般引用随机或者模糊技术。但在实际问题中，概率分布和隶属函数往往是不可知的[1-2]，因此近年来区间线性规划得到广泛研究。然而，对于求最优解相对应的约束矩阵的问题，目前所得方法只能针对最优解求出唯一的一组约束矩阵[3]。区间线性规划可分为3种形式[4]，本文对带有区间线性方程组的问题进行讨论，在原方法的基础上进一步研究，从而构造出一个最优解所对应的无数多组约束矩阵。

1 准备知识

矩阵A≤B是指A的每个分量小于等于B 中对应的分量，A=(aij)的绝对值为|A|=(|aij|)。

下列定义与文献[6]所给出的相同。

定义1 给定A∈Rm×n，b∈Rm，c∈Rn，问题称为一个线性规划问题，可简写为称A，b为约束矩阵，c为目标函数的系数。称D ={x|Ax≤(=，≥)b，x≥0}为可行域，x∈D为该问题的可行解。若该问题可行域非空，且它有一个可行解x*∈D 使得cTx*≤cTx，x∈D，则称x*是该线性规划问题的最优解。

任取A∈AI，b∈bI，c∈cI，得到问题Min{cTx|Ax≤(=，≥)b，x≥0}，称它的一个最优解为式(1)的一个最优解，相应的最优目标函数值为式(1)的一个最优值。本文讨论问题如下:

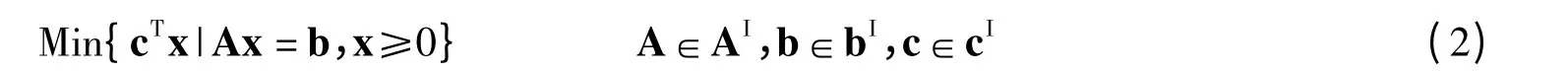
设向量y∈Rm，定义

由文献[3]可得引理及定理1 如下:

x*是式(3)的一个最优解，则有:

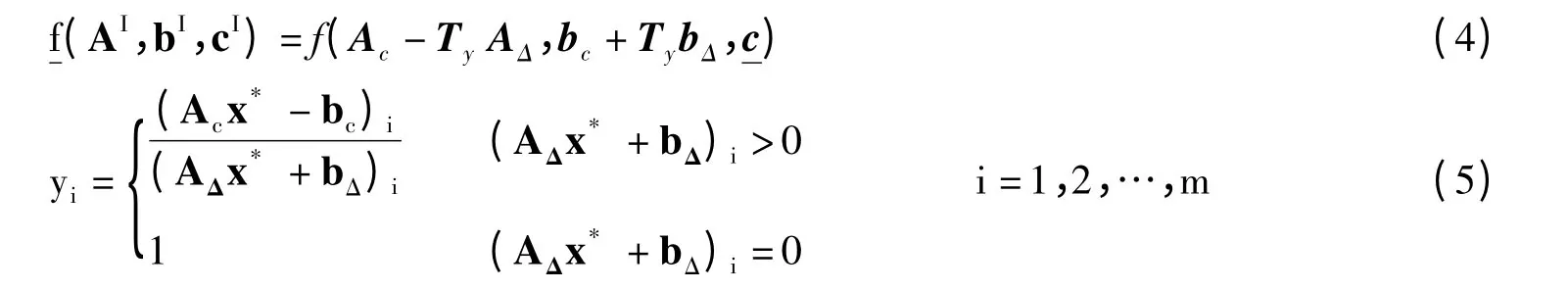
2 主要结果

计算最优值区间是区间线性规划的一个常见的问题，相关研究见文献[5]、文献[7]。而人们一般会对什么情况下取到最优值感兴趣，本文讨论的就是式(2)最优值的下界在哪些情况下可以取到的问题，也就是求出式(3)的一个最优解所对应的目标函数系数及约束矩阵。本文在文献[3]中对该问题的研究基础上进行拓展，得到以下结论。

x*是式(6)的最优解，且有式(4)成立，其中:

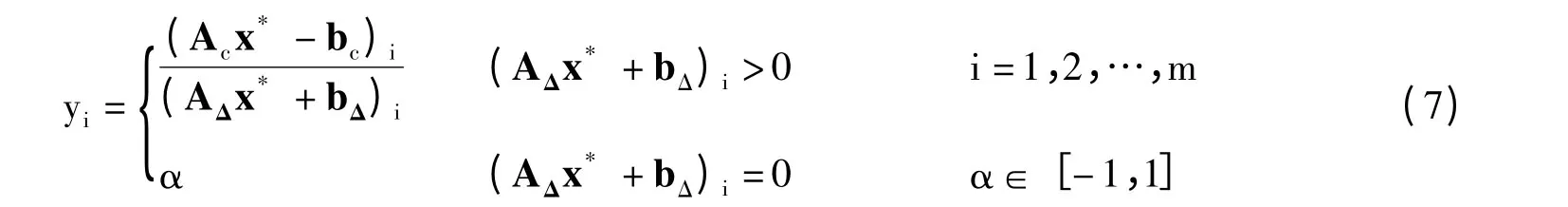
对于向量y∈Rm，由式(7)、(8)知，且Acx*-bc=Ty(AΔx*+bΔ)，则(Ac-TyAΔ)x*=bc+TybΔ，所以x*是(Ac-TyAΔ)x =bc+TybΔ，x≥0的一个可行解。而由|y|≤e可知所以可得不等式因此即x*是式(6)的最优解，且式(4)成立，证毕。

由定理2可知，yi可以有无穷多种取值，随之就有无穷多种约束矩阵，但不论Ty怎么变，也就是约束矩阵怎么变，x*都是它们所确定的线性规划问题的最优解，这也就是说在最优解、最优值不变的前提下，可以构造出无穷多组约束条件。

3 算例

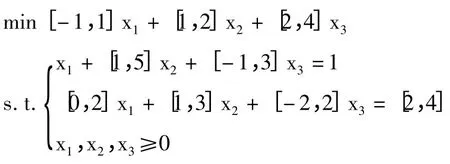
例 求区间线性规划问题的最好最优值，及最好最优

解对应的目标函数系数和约束矩阵。

解 由文献[6]提出的最好最优解模型可得本问题的最好最优解模型为:

解式(9)求得最好最优解与最好最优值分别为x*=(1，0，0)T，z*=-1。易知计算得由定理1 即原方法可得y1=1，y2=-1，从而进而可得最好最优解x*对应的目标函数系数为c' =(-1，1，2)T，约束矩阵而用定理2 即本文所得的新方法可得到y1=α，α∈[-1，1]，y2=-1得到c″=c'，b″=b'，不同的是约束矩阵A″ =其中β∈[1，5]，γ∈[-1，3]。

4 结束语

本文构造出了在带有区间线性方程组的区间线性规划问题中一个最优解所对应的无数多组约束矩阵。通过实例演示，体现出了本文所得方法与原方法的不同及与之相比的优势所在。同时可以看出，本文所得方法不仅具有理论价值，也具有较强的实用价值。

[1]Oliver Chukwudi Ibe.Fundamentals of Applied Probability and Random Processes[M].London:Access Online via Elsevier，2005:59-76.

[2]谢季坚，刘承平.模糊数学方法及其应用[M].武汉:华中科技大学出版社，2000:1-72.

[3]Fiedler M，Nedoma J.Linear optimization problems with inexact date[M]，New York:Springer，2006:35-92.

[4]Hladik M.Linear Programming—New Frontiers in Theory and Applications[M].New York:Nova Science Publishers，2011:1-46.

[5]Hladík M.Optimal value range in interval linear programming[J].Fuzzy Optimization and Decision Making，2009，(8):283-294.

[6]李炜.线性优化及其扩展[M].北京:国防工业出版社，2011:200-212.

[7]Chinneck John W，Ramadan K.Linear programming with interval coefficients[J].Journal of the Operational Research Society.2000，51(7):209-220.