基于粗糙集方法的决策树多值偏向理论分析

(浙江工业大学信息工程学院，浙江 杭州310023)

0 引 言

决策树方法是最受欢迎的数据挖掘技术之一，主要用于分类和预测。学者提出了著名的ID3 决策树分类方法[1]。然而实验表明ID3算法在构造决策树时有多值偏向的问题，以往大多数的学者都是通过实验研究多值偏向问题[2-5]。有学者首次提出一种理论分析多值偏向问题的方法[6]。然而文献[6]在分析多值偏向问题时，理论的严密性及逻辑性不强，缺少实例验证。本文在文献[6]基础上，针对其不足，基于粗糙集理论引入属性重要度概念，从理论上分析了属性多值对信息熵的影响和属性多值对其他属性的重要性程度的影响两个问题。最后通过实验表明理论分析方法的正确性与可行性。

1 ID3算法及粗糙集理论

1.1 ID3算法

算法的主要思想[7]:已知数据样本集S，样本个数s，样本所属类别集合为C，设共有m个{c1，c2，…，cm-1，cm}，把S 分为m个样本子集为S={S1，S2，…，Sm-1，Sm}，样本集Si中样本的个数为si。样本集的信息熵表示为:

设样本集集合S 中某个属性为A，A 有n个不同的属性值{a1，a2，…，an-1，an}。基于A的属性值把S划分为n个样本子集:S={S1，S2，…，Sn-1，Sn}，sij表示为Sj(j=1，2，…，n)中属于类ci(i=1，2，…，m)的个数，pij表示为样本子集Sj中样本属于有类ci的概率:

子集Sj的信息熵为:

根据属性A 划分后的样本集合的信息熵为:

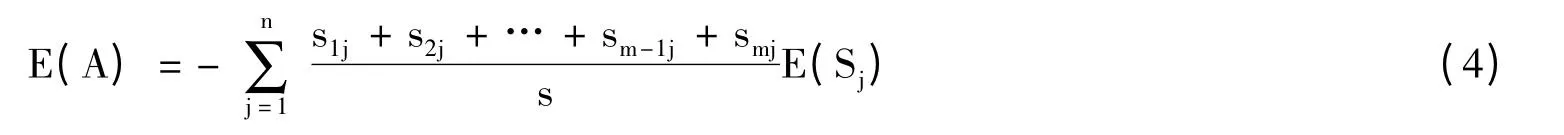
信息增益:

选择属性对结点进行划分的标准就是选取信息增益最大的属性。

1.2 粗糙集理论及属性重要度

定义1 在信息表S中，对于属性集I⊆A，可构成对应的二元等价关系:

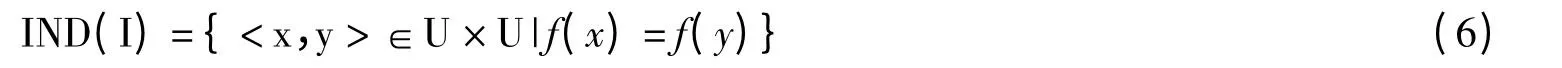
式中，f(x)表示对象x 在属性I 上的属性值，称为由I 构成的不可分辨关系。

定义2 设X⊆U，A为属性集合，X的A的下近似的定义:

式中，U/IND(A)表示对象集合关于属性集合A的等价类集合。表示一定属于X的对象集合。X的A的上近似的定义为:

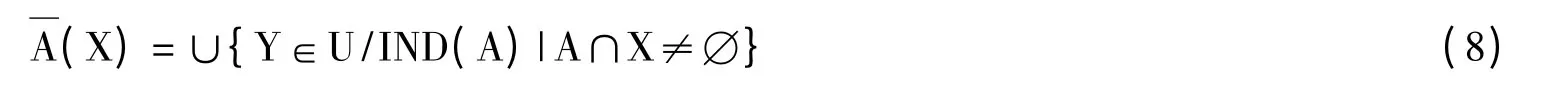
定义3 在信息表中，存在属性集P，Q⊂A，定义Q的P 正域表示为:

定义4 在信息表中，存在属性集R⊂C，定义D 依赖于R的程度为:

定义5 存在属性集R⊂C 及属性r∈R，定义属性重要性度为:

式中，Card(POSR(D))表示集合的基数，属性重要度表示属性r 在条件属性集R 中对样本分类的重要性程度。其中D为决策属性。

2 多值偏向及属性重要度分析

设A是样本集的某个属性，具有n个属性{A1，A2，…，An-1，An}，该属性把样本集合S划分为S ={S1，S2，…，Sn-1，Sn}。现在把属性值为An的样本随机的分拆为属性值分别为A'n，A'n+1的样本子集，与A1，A2，…，An-1构成新的属性A'，A'有n+1个属性值:{A1，A2，…，An-1，A'n，An}，A'把样本集S划分为S={S1，S2，…，Sn-1，S'n，Sn+1}。

2.1 算法多值偏向理论分析

思路:比较分裂前后属性A的信息熵大小及重要度，即Gain(S/A')和Gain(S/A)的大小及与I(A)的大小。

1)由粗糙集理论可知:

2)为方便计算，用p(ci/Aj)=pij，即表示属性值等于Aj时样本集属于C =ci的概率。用p(Aj)表示属性值为Aj时样本子集的权值。比较Gain(S/A')与Gain(S/A)的大小。

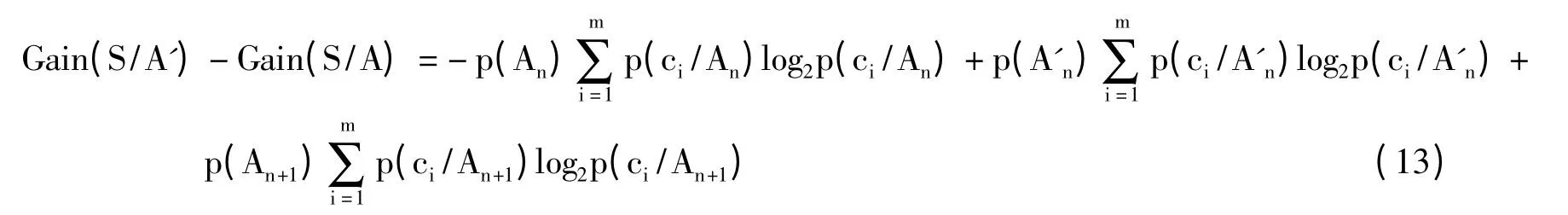
对上式等式两边同除以p(An)，得:

由式(12)、(15)得:I(A')=I(A) Gain(S/A')≥Gain(S/A)，证明完毕。

2.2 属性多值对其它属性重要度的影响

假设属性集为{A，B，C}，拆分属性A的一个属性值，然后计算属性C的重要性程度。

式(17)、(18)中，Xn=X'n∪Xn+1。

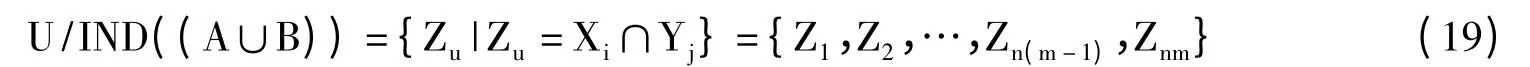
式中，Xi属于U/IND(A)，Yj属于U/IND(B)。

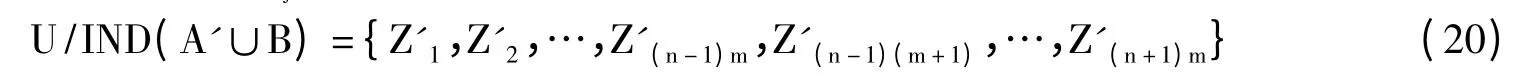
式中，Xi属于U/IND(A')，Yj属于U/IND(B)。

式(19)、(20)中，Zi=Z'i(i=1，…，(n-1)m)，Znm=Z'(n-1)m∪Z'(n-1)m+1∪…∪Z'(n+1)m。{A，B，C}及{A'，B，C}中C的重要度分别为I(C，{ABC}，D)其中，Card(POSABC(D))=Card(POSA'BC(D))，所以只需决策树要比较Card(POSAB(D))与Card(POSA'B(D))的大小。

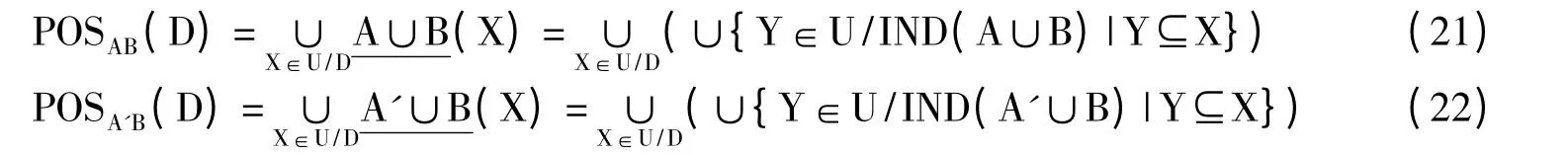
比较式(21)、(22)，得到Card(POSAB(D))≤Card(POSA'B(D))，最终得到I(C，{ABC}，D)≥I'(C，{A'BC}，D)。证明了属性集合中的某属性的增加属性降低其他属性的属性重要性程度。

3 实例

以下实例是判断气候各个因素是否适合外出旅游，如表1所示。

设U为全体样本，Q={d}，P={a1，a2，a3，a4}为条件属性集集合。

这里只计算属性a1熵与a4的重要性属性，拆分a5=rain的属性值，形成新的属性a'1，计算a1分裂前后a1的信息增益，得Gain(U/a1)=0.246，Gain(U/a1')=0.298。计算a1分裂前后的属性a4重要度为:I(a4)=0.286，I(a4)' =0.143。实验结果验证了理论分析的正确性。

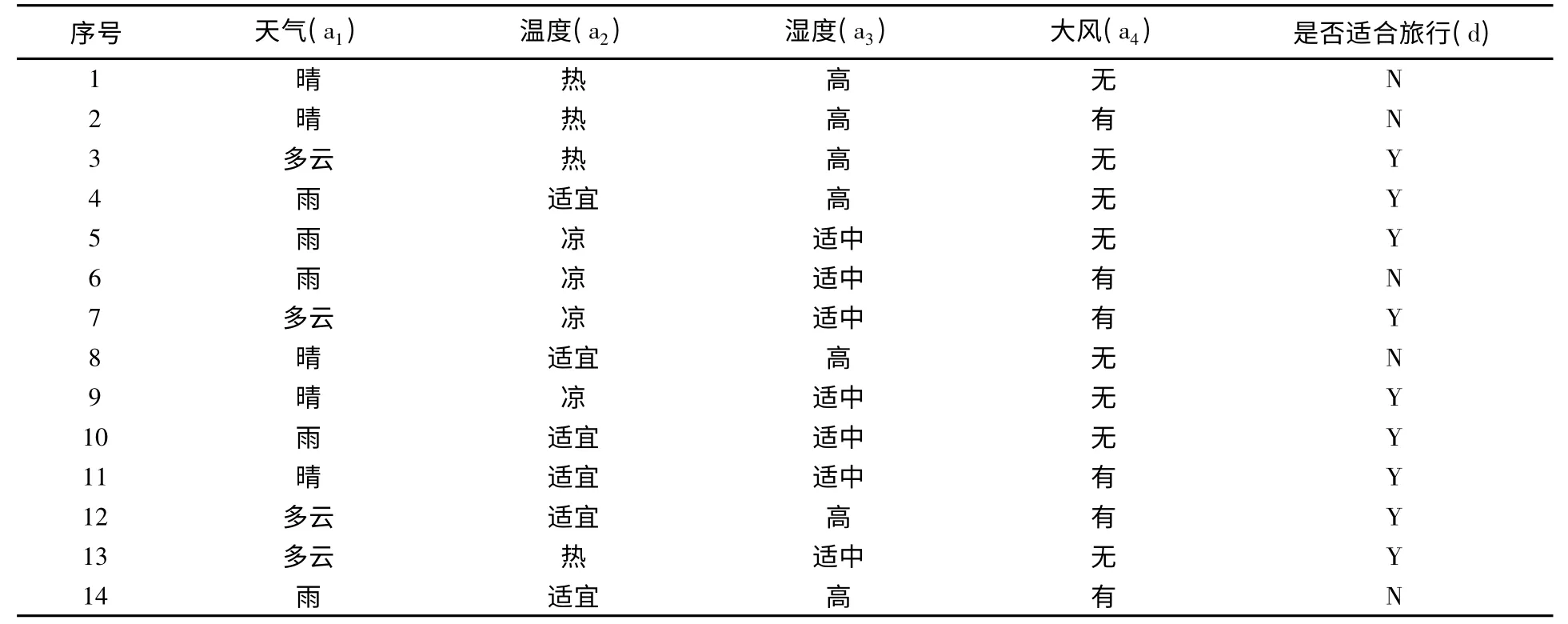
表1 气候因素表

4 结束语

本文从理论的角度分析了决策树ID3算法的多值偏向问题。基于粗糙集理论，引入属性重要度，证明了属性在增加属性值的时候，属性信息熵增加，但是该属性的属性重要度没有增加。本文最后还分析了属性增加属性值对其他属性重要度的影响。本文的不足之处是没有提出克服决策树ID3 多值偏向的方法，下一步工作重点是修正决策树ID3算法的多值偏向问题。

[1]Quinlan J R.Induction of Decision Tree[J].Machine Learning，1986，(1):81-106.

[2]刘小虎，李生.决策树的优化算法[J].软件学报，1998，9(10):797-800.

[3]胡学钢，张冬艳.基于粗糙集的混合变量决策树构造算法研究[J].合肥工业大学学报(自然科学版)，2007，30(3):257-260.

[4]朱颢东.ID3算法的改进和简化[J].上海交通大学学报，2010，44(7):883-886.

[5]张琳，陈燕，李桃迎，等.决策树分类算法研究[J].计算机工程，2011，37(13):66-67.

[6]韩松来，张辉，周华平.决策树算法中多值偏向问题的理论分析[C].北京:中国金属学会，2005:133-140.

[7]Ding Baoshi，Zheng Yongqing，Zhang Shaoyu.A New Decision Tree Algorithm Based on Rough Set Theory[C].Wuhan:Asia-Pacific Conference on Information Processing，2009:326-329.