架空线张力与频率关系理论与试验的研究*

谢占山，李忠芳，王少夫

(安徽科技学院)

0 引言

输电线路是输入电能的通道，其安全可靠的运行，是保证国民经济平稳发展的因素之一．然而输电线路是一个系统，它包括塔基、杆塔、绝缘子、金具、架空线、避雷线等其他辅助设施，在此些系统中，架空线是输送电能的载体，是整个输电系统的核心组成之一;架空线在运行中，由于受到外界因素的影响(譬如风载荷，浮冰、雾凇载荷，大气温度等)影响以及导线自身温度影响，导致其本身张力变化较大进而导致其频率特性变化剧烈，若某工况下架空线的频率与输电铁塔的固有频率相同或者相近，那么很容易造成铁塔的倒塔现象的发生，所以开展架空线张力与频率关系的研究显得必要的［1］．

架设架空线使用张力放线机，在当时施工的环境下，张力的大小的是确定的，即此时的架空线固有频率是定值，但是架空线工作环境复杂，容易受到外界因素的影响，其本身的张力呈现较大幅度变化范围，这就造成架空线本身频率的波动，所以在设计线路以及铁塔设计时，有必要评估一定档距的架空线在各类极端载荷的下频率范围，尽量绕开其频率范围，以防止共振的发生．

架空线是通过钢芯(碳纤维)与铝合金的导线绞制而成，因此架空线的子导线是一个复杂的柔性体或者复合索特性的结构体．为了弄清架空线在不同外载荷下其张力与频率函数关系，该文将从理论方面进行推导架空线张力与频率的关系，在实验室条件下进行不同张力情况下架空线频率的测定，以揭示张力与频率的关系，验证理论的正确性，为铁塔设计、架空线档距最佳距离确定及其与铁塔匹配具有重要的意义．

1 架空线张力与频率之间关系的理论与试验研究

1．1 架空线振动方程

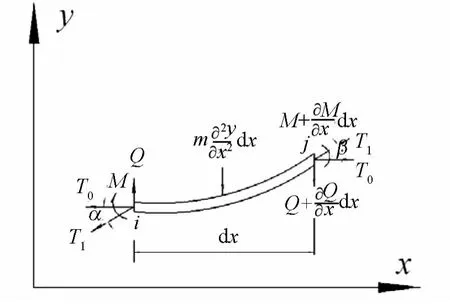
图1 有刚度无阻尼架空线微单元的受力示意图［2，3］

如图1所示，架空线微单元的长度为dx，刚度为 EI，水平张力 T0，i、j节点的轴向力分别为Ti、Tj，单位长度的质量为m，微单元dx长度上有弯曲，其平衡方程如下:

(13)的通解为:T(t)=Asinλt+Bcosλt

平均档距为500 m的单根架空线悬挂在线夹下，其自重可达半吨左右(如6分裂的LGJ-300/40 自重约为3．4 t)［4］，整个子导线处于绷紧的状态，在线夹处其边界条件为:

由式(25)可知，架空线在架设时，其张力与固有频率是定值，但是架空线在运行是会受到外界因素的影响，而导致张力变化，进而导致其频率随之变化，此时可以根据(25)进行评估．

1．2 实验室条件下张紧架空线张力与频率试验研究

1．2．1 线路上档距内架空线边界条件确定

在线路上运行的架空线被固定在绝缘子下端的线夹处，其纵向及横向位移为零，绝缘子在相邻档距的架空线自重的作用下，其基本与水平面处于垂直，同时架空线也处于绷紧的状态，故在实验室的条件下将钢绞线紧固，以防止其发生横向及纵向的位移．

因架空线所处的地形不同，架空线档距不同，一般情况下输电线路档距通常在100～1000 m之间［4］;输电线路的输送功率不同，所用的子导线数以及导线型号不同，因此架空线的张力不同，故在实验室的条件下需将架空线的一端设定一个可调节张力大小的装置，以实现不同张力．

1．2．2 实验室条件下导线张力与频率试验研究

为了研究架空线张力与频率的数值关系，实验室条件下选用某型号的钢绞线，其一端紧固在可调节张力大小的试验台上［5］，另一端固定在与试验台连接的力学传感器上，架空线中间部位布置一加速度传感器(如图2所示)，其中张力传感器(如图3所示)用来测定钢绞线的张力，加速度传感器(如图4所示)用来测定钢绞线档距四分之一、八分之一处的加速度，其后进行数据分析，得到的不同张力情况下频率，如表1所示．

图2 钢绞线张力调节端

图3 钢绞线张力测定端

图4 加速度传感器布置位置

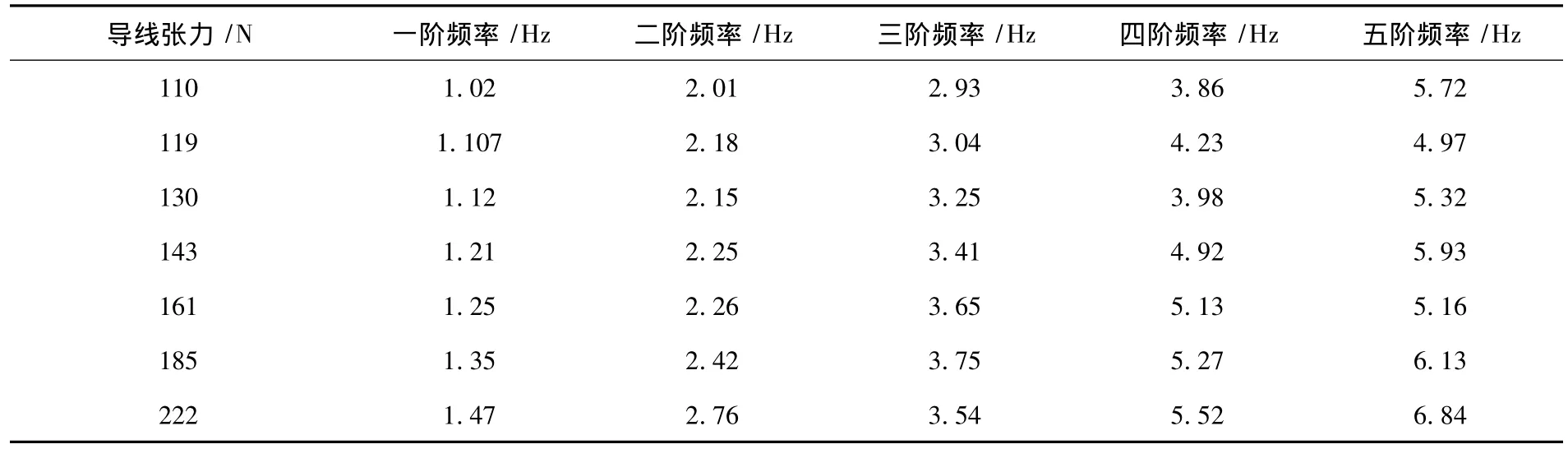
表1 实验室条件下不同张力的导线的振动频率

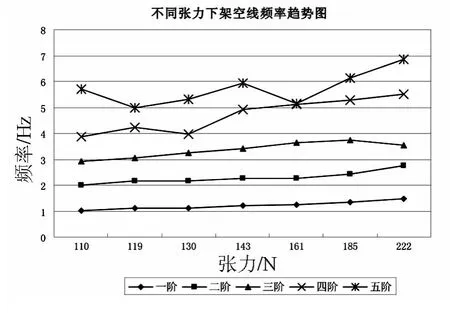
图5 实验室条件下架空线张力与频率关系图

由表1和图5可以看出，相同张力的情况下，相邻的频率的之差近似为第一阶频率，这是因为架空线各股之间有摩擦，存在一定阻尼．随着张力的增加，各股之间的摩擦阻尼随之变化，各阶次频率随着张力的增大而总体增大，虽然图中三阶与五阶频率有下降的数值点，但是不影响架空线张力增大频率增大的趋势，下降的数值点，可能是因为试验误差导致．

上述实验数据与分析与理论分析基本相吻合，验证了理论假设的正确性，同时也证明了实验方法的可行性．

2 结束语

通过对架空线振动方程的分析，得出了架空线的张力及微单元长度质量为某定值时，第n阶振动频率是第一阶频率的n倍，相邻的两阶固有频率之差是第一阶的振动频率．实验数据分析可知，架空线各股之间存在阻尼，张力的大小对各股之间的阻尼有影响，但不同张力之比近似等于同阶次的频率之比的平方;频率与张力的之间的关系反映了架空线的张力随导线的张力增大而增大，因此在架空线运行中了解张力的并控制张力，对于保护线路安全具有重要的工程意义．也铁塔设计、架空线档距最佳距离确定及其与铁塔匹配具有重要的意义．

［1］ 王冬．架空线路的舞动分析和扰流防舞器的研究［D］．华北电力大学，2011．1-2．

［2］ 孟遂民．架空输电线路设计［M］．北京:中国电力出版社，2007．

［3］ 刘荣英．偏微分方程在弦振动问题中的应用［D］．华中师范大学，2007．4-18．

［4］ 谢占山．500 kV“V”串复合绝缘子机械疲劳试验研究［D］．华北电力大学，2012．1-12．

［5］ 张旺海．覆冰架空导线振动数值仿真分析及实验研究［D］．华北电力大学，2012．29-33．