基于哈希算法的图像拷贝检测*
马庆贞 王云飞 曾宇鹏 郑创伟 陈宇辉 谢志成
(1.华中科技大学计算机科学与技术学院 武汉 430074)(2.深圳报业集团福田区深南大道6008号报业大厦 深圳 518009)
1 引言
多媒体数据的快速传播和共享使得媒体数据的版权保护成为当前亟待解决的问题。拷贝检测技术是版权保护的一种有效手段。目前广泛使用的拷贝检测技术主要有数字水印和基于内容拷贝检测两大类方法。
数字水印有以下缺点:对未嵌入水印的作品无法进行拷贝检测;受到攻击的水印不能有效地用于拷贝检测和版权认证。对多媒体作品进行攻击的重要前提是不能影响其商业价值,也就是作品的内容不能有很多的变化,这使得基于内容的拷贝检测成为了最有应用前景的版权保护技术之一。本文主要研究基于哈希算法的图像拷贝检测。
在图像拷贝检测中,图像特征一般维度较高,并且大多图像库拥有海量数据,使得现有的拷贝检测技术性能低下。鉴于上诉分析,本文提出了:1)基于局部保持投影的降维算法的优化,将高维特征映射到低维空间中,在解决维度灾问题同时避免了过拟合;2)基于最大熵模型的二值化处理;3)最优的哈希码的长度和汉明距离选择策略。
1.1 局部保持投影(LPP)
局部保持投影(LPP)[1,10]用谱图理论[2]来 阐述,其基本思想是用谱图G=(V,E)模拟空间中样本点的局部几何结构,在一定程度上保持了数据集中样本间的内在局部位置结构。
给定子流型结构中的m个样本点组成的数据集X={x1,x2,…,xm|xi∈Rn},寻找变换矩阵A将其映射到低维空间Y={y1,y2,…,ym|yi∈Rl}。保持局部几何结构的最佳映射的优化准则为
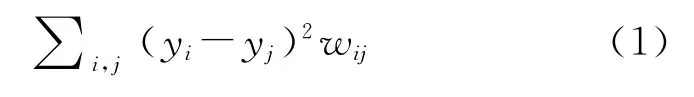
其中wij表示xi和xj间的边权重。通过简单的代数变换,式(1)可以转化为
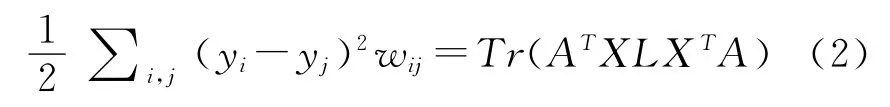
其中拉普拉斯矩阵L=D-W,D为对角矩阵,Dii=∑jwij,Tr(.)表示矩阵的迹。限定条件:

式(2)在约束条件下的最优问题转化为广义特征值分解:
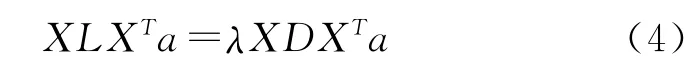
按升序排列特征值λ0≤λ1≤…≤λl-1,对应的特向量组成最优投影矩阵A=(a0,a1,…,al-1)。
1.2 最大熵模型(EM)
最大熵理论[3~4,8]指出当根据不完整的信息推断最吻合样本数据分布的解时,应该由满足分布限制条件的具有最大熵的概率分布推得。对于训练数据集D={(x1,y1),…,(xn,yn)},随机事件的不确定性可用条件熵来衡量:
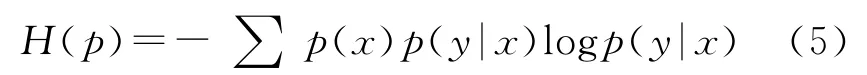
使得熵最大的概率分布p必须受到特征函数的限制,其一般形式为

最大熵模型有其他模型无法比拟的优点[5,11]:首先,最大熵统计模型获得满足约束条件的信息熵极大的模型;其次,最大熵统计模型可灵活地设置约束条件,通过约束条件调节模型对未知数据的适应度和对已知数据的拟合度;最大熵模型解决了统计模型中参数平滑问题。
2 哈希算法
基于哈希算法的图像拷贝检测的流程如图1所示。先从原始图像库提取全局特征并进行降维处理;然后将特征序列转换为哈希码;最后为特征序列建立索引。对于查询图像,根据相同的方法用哈希码表示图像,然后在索引中查询相似的特征序列,并返回查询结果。其关键技术有高维向量降维的优化、二进制向量编码及检索。
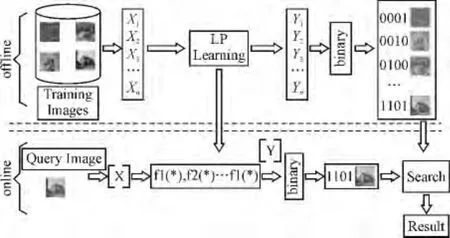
图1 基于哈希算法的图像拷贝检测流程图
2.1 局部保持投影优化
在拷贝检测中,先在训练集得到LPP 的映射矩阵,然后利用映射矩阵将新样本映射到低维空间。由于此映射矩阵可能产生过拟合,在原有LPP算法的基础上加入正则化:
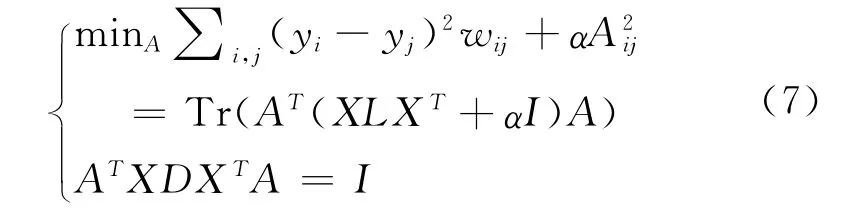
利用广义特征值分解可求解式(7)。通过调节参数α可得到很好描述新数据集的特征映射矩阵。图2为α取不同值的PR 曲线,从图中可知,当α=-1000时,系统有较好的查询性能,表明我们得到的投影矩阵有较好的泛化能力。
该降维算法具有如下优点:
· 适用于信息检索应用。在投影前后保持数据内在的结构信息,便于创建索引结构。
· 拉普拉斯特征映射的线性逼近(LE)[6],相比非线性的降维技术计算速度更快。
· 在LPP的基础上加入正则化,可防止产生过拟合。
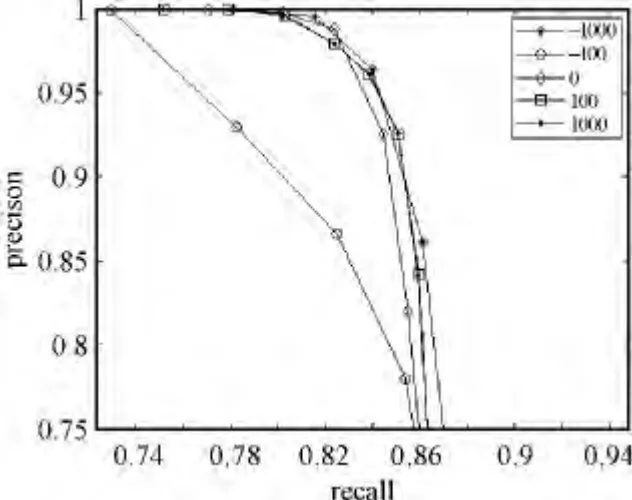
图2 不同参数下的PR 曲线
2.2 基于EM 的二值化处理
二值化处理将低维特征映射至海明空间,生成便于计算和存储的二进制哈希码。相邻的特征能够被映射为相似的哈希码。下面介绍如何将低维空间特征转化为二进制哈希码。
给定N维特征向量x=(x1,x2,…,xN),计算特征向量的均值然后将特征向量的每一维与均值进行比较:
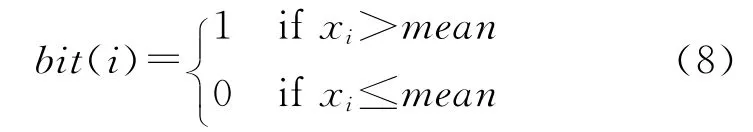
经过上述处理,低维空间的特征被转换为二进制哈希码。在海明空间内进行检索时一般采用遍历方法展开近邻搜索,查找查询半径以内的所有码字,然后返回对应容器中的对象。
这种处理的最大优势在于:数据间的海明距离可通过计算机硬件的“异或”操作实现,计算千万数量级数据的海明距离所需的时间只在毫秒级。此外,低维的哈希码大大降低了存储开销,千万级数据所对应的索引信息可全部载入内存,保证了检索算法的高效性。
3 实验结果及分析
3.1 拷贝检测质量评价标准
对于图像拷贝检测,我们感兴趣的是检测到的对象数量和检测错误的概率,因此用P-R 曲线作为检测质量的评价指标。P-R 曲线[7]以查准率为纵坐标,查全率为横坐标绘制。查准率反映检索系统拒绝非相关信息的能力,用公式表示为
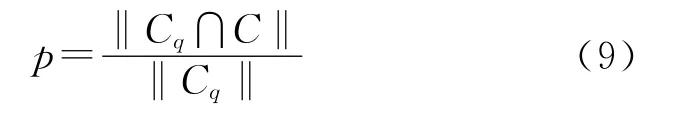
查全率反映的是检索系统和检索者检出相关信息的能力,用公式表示为
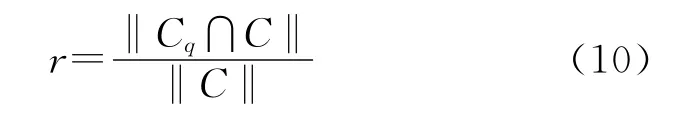
其中C为图像库中拷贝图像集合,Cq表示被认为是拷贝图像集合,‖‖代表集合中元素个数。
为了确定哈希码的长度,我们利用F1-measure[7,9]指标。F1-Measure是对准确率和召回率的综合评价指标,表示在不同的汉明距离下,查全率和查准率随编码长度变化的趋势。
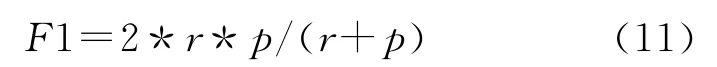
其中r为recall,p为precision。
3.2 码字长度及汉明距离
对于一幅图像,我们最终将其特征转化为二进制哈希码。哈希码的长度L是第一步要确定的问题。当L太小时,不同的特征序列会转换成相似的01序列,使得系统的查全率和查准率较小;而当L太长时,虽然能获得较好的性能,但构建索引需较大的内存。
我们从1~195改变编码长度,汉明距离从0~3。图3为F1-Measure在随编码长度变化而呈现的变化趋势。从图中可知,随着汉明距离的变大,F1-Measure的峰值会变大;并且在达到峰值之前,F1-Measure逐渐变大,随后逐渐变小。
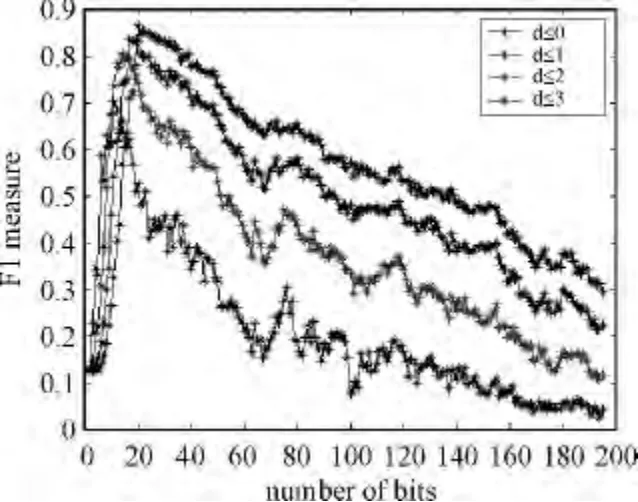
图3 F1-Measure随编码长度和汉明距离的变化趋势
下面在不同的编码长度下测试的最佳查全率和查准率。各PR 曲线的最优检测结果如表1所示。综合查询性能与空间复杂度,将编码长度设置为40,此编码长度可以使系统具有较好的查询性能并且具有较低的空间复杂度。
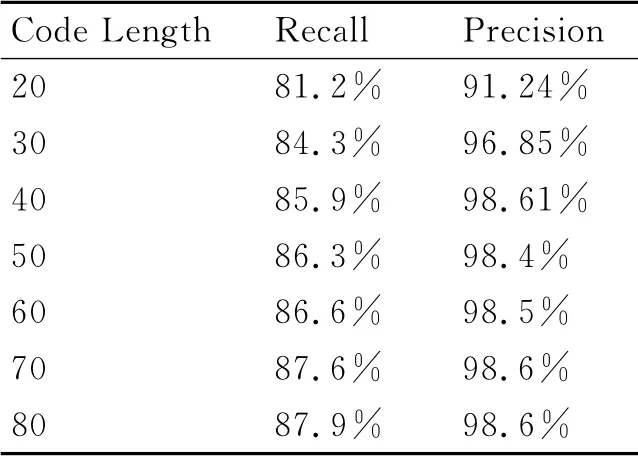
表1 不同编码长度下的最优检测结果
下面通过虚警率和漏警率来测试在编码长度为40的情况下,如何选择汉明距离使得系统具有较高的查全率和查准率。虚警率是指误检的图像个数与检测出的图像数目的比例;漏警率是指没有检测出的拷贝数目与全部拷贝数目的比例。其公式如下:
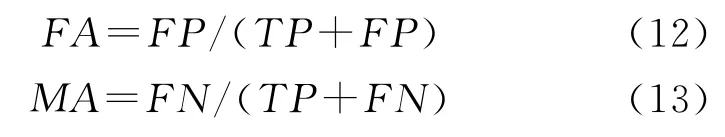
其中,FP为误检的图像数目,TP为正确检测出的图像数目,FN为漏检的图像数目。
通过分析可知,拷贝图像与原始图像的汉明距离较小,并且当汉明距离等于零时,检测出的拷贝图像所占比例应该是最多的;非拷贝图像与原始图像的汉明距离较大。
我们用2W 的测试数据集,包括1W 幅拷贝和1W 幅非拷贝图像。其中的1W 幅拷贝是通过对原始图像进行stirkmark攻击后得到的。我们计算原始图像的特征序列与拷贝图像和非拷贝图像特征序列间的汉明距离,然后统计各汉明距离中图像个数占全部图像数目的比例。
从图4可知,当汉明距离等于0时,拷贝图像的个数比例最高;随着汉明距离的变大,拷贝图像的个数所占的比例逐渐变小。当汉明距离等于20时,非拷贝图像所占的比例达到峰值。使得虚警率和漏警率组成的面积最小的汉明距离即为最优的汉明距离。可以看出,当汉明距离为10时,可以得到较高的查全率和查准率。
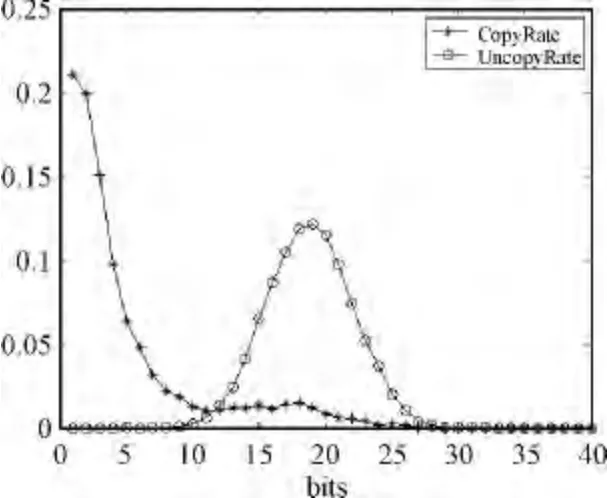
图4 汉明距离优化
4 结语
本文介绍了LPP 的优化算法,实现了将高维特征线性映射到低维空间,同时保持数据的局部内部结构。最后,对得到的低维特征进行二值化处理,得到特征的哈希码。为了平衡查询性能和查询效率,我们通过实验选择最优哈希码长度,并在此基础上确定汉明距离。
[1]He,Xiaofei,Partha Niyogi.Locality preserving projections[C]//NIPS,2003,16:234-241.
[2]Cvetkovic,D.M.,et al.Recent results in the theory of graph spectra[J].North Holland,1988,36:193-211.
[3]Smadja,F.Retrieving collocations from text:Xtract[J].Computational linguistics,1993,19(1):143-177.
[4]Church,K.W.,P.Hanks.Word association norms,mutual information,and lexicography[J].Computational linguistics,1990,16(1):22-29.
[5]Berger,A.L.,Pietra,V.J.D.,Pietra,S.A.D.A maximum entropy approach to natural language processing[J].Computational linguistics,1996,22(1):39-71.
[6]Belkin,M.,P.Niyogi.Laplacian eigenmaps and spectral techniques for embedding and clustering[J].Advances in neural information processing systems,2001,14:585-591.
[7]Powers,D.M.Evaluation:From precision,recall and f-factor to roc,informedness,markedness &correlation[J].School of Informatics and Engineering,Flinders University,Adelaide,Australia,2007,Tech.Rep.SIE-07-001.
[8]S.Baluja,M.Covell.Learning to hash:forgivinghash functions and applications[C]//Data Mining and Knowledge Discovery,2008,17(3):402-430.
[9]C.D.Manning,P.Raghavan,H.Sch¨utze.Introduction to information retrieval[M].volume 1.London:Cambridge University Press,2008.
[10]Zhang,L.,Qiao,L.,Chen,S.Graph-optimized locality preserving projections[C]//Pattern Recognition,2010,43(6):1993-2002.
[11]Ratnaparkhi,Adwait.Maximum entropy models for natural language ambiguity resolution[D].Pennsylvania:University of Pennsylvania,1998.

