基于λ-等效原则的并联系统备件配置方法*
(海军工程大学兵器工程系 武汉 430033)
1 引言
备件配置优化,即为装备确定备件品种和数量最合理的配置,以在有限的资源约束条件下实现最大的备件供应效能,或者以最小的资源实现要求的供应效能水平[1~2]。对于工程中由多部件组成的系统而言,为了确保其连续工作能力,通常会对其配置一定数量的备件。在配置过程中,为了使系统具备较高的连续工作能力,往往需要配置较多的备件,这就产生了高额的保障费用(如采购和库存费用)。而配置备件较少,又会频繁出现备件短缺的情况,导致系统不可用。因此,在有限经费条件下,如何合理地配置备件以满足系统的使用要求,具有重要的经济意义和使用价值。
针对由不同寿命分布类型不可修部件组成的系统,国内外学者开展了大量的相关研究。通过综合考虑系统的战备完好性或任务可靠度,以及保障费用等条件建立了相应的备件配置模型,并且通过采用边际效益、动态规划或遗传算法等优化算法对备件配置方案进行了优化。如文献[1]针对部件服从任意寿命分布的多部件系统,提出了基于蒙特卡罗仿真-边际效益分析的备件配置优化算法。文献[3]综合考虑备件的费用、体积和质量等因素,提出了系统保障度分配模型并采用动态规划的优化方法得到备件的配置方案;文献[4]利用边际效益方法和仿真优化方法解决备件配置优化问题的思路;文献[5]针对Weibull分布型多部件备件组成的串联系统,提出了备件需求量的改进算法。尽管上述方法成功地解决了部分问题,但存在一定的适用性。比如大部分文献[6~7]仅研究了指数寿命分布组成的系统的备件配置问题,对于实际中存在的不同寿命分布类型组成的系统备件,由于其自身的复杂性(寿命规律不同),导致备件配置模型十分复杂,往往仅能通过仿真手段进行求解。特别是对于并联系统而言,由于结构的特殊性,导致较少文献对其进行研究。由此可见,针对多寿命分布类型组成的并联系统,如何建立其备件配置优化模型,从而可以准确、直观地获得备件优化解析解尚需进一步研究。
针对由不同寿命分布类型部件组成的并联系统的备件配置问题,首先依据累积失效相等原则,将不同寿命分布部件等效为指数型部件;然后在此基础上建立以系统保障度为约束条件,以保障费用为目标的数学模型,并利用边际效应算法,对不同寿命分布类型的部件的备件配置数量进行了优化求解;最后通过具体案例的应用,对计算方法进行了进一步的说明和检验。
2 非指数分布等效为指数分布方法
2.1 λ-等效原则
衡量一种分布的基本参数包括失效率、平均寿命、可靠度等。已有的文献研究表明,尽管平均寿命等效方法对于非指数型备件的数量确定具有适应性,但具有保守性。但如果按照这种方法进行备件需求预测,方便的同时又会造成备件的浪费,有时甚至是过度浪费。通过数值分析表明了,累积失效相等方法由于具有较高的近似精度而更加适合舰船装备备件需求数量的确定[8~9]。
所谓失效率是指部件在工作到给定时间后,单位时间内发生故障的概率。若部件的寿命分布函数为F(t),其失效率函数为λ(t),平均寿命为μ,则其在(0,t]时间内平均故障累积函数(Cumulative Hazard Function,CHF)为

平均故障累积函数反映了备件在时间t内的平均故障次数。当该分布为指数型分布时,有H′其中λ′为常数。若采用平均故障累积函数相等原则,将非指数分布等效为指数分布时,即要求H(t)=H′(t)=λ′t,得到

称上述等效原则为累积失效相等原则,简称λ-等效原则[10]。通过该方法,可将非指数型分布等效成失效率为常数的指数分布,表明在相等时间内平均累积故障次数相等。
2.2 非指数型分布备件的λ-等效方法
根据文献[5]的推导计算,分别有威布尔分布、正态分布、伽马分布型备件的λ-等效方法如下:
1)威布尔型备件的λ-等效方法
对于服从参数为(β,λ)的威布尔型分布备件,当形状参数β>1时,其平均寿命为(1+1/β),失效率可等效为λ1=λtβ-1。
当保障时间T≤μ时:

当保障时间T>μ时:

2)正态型备件的λ-等效方法
对于服从(μ,σ)的正态型备件,其失效率可等效为
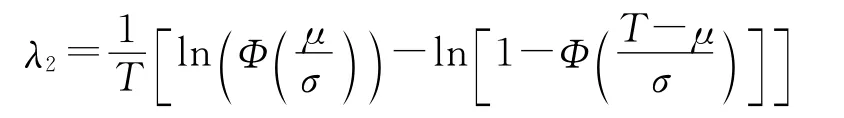
当保障时间T≤μ时:
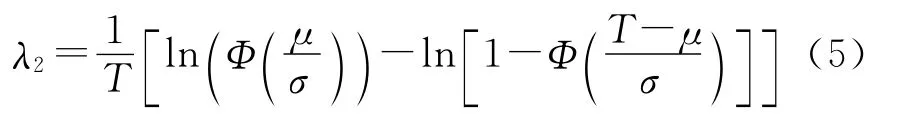
当保障时间T>μ时:
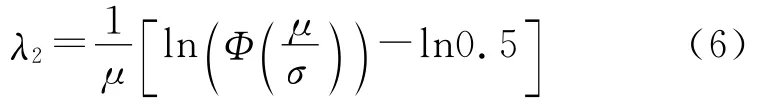
3)伽马型备件的λ-等效方法
对于服从(α,λ)的伽马型备件,其平均寿命μ=α/λ,失效率可等效为
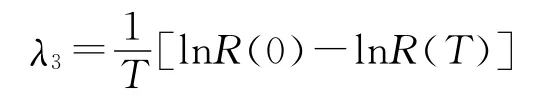
当保障时间T≤μ时:
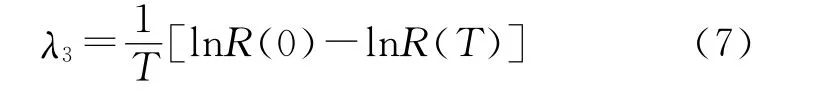
当保障时间T>μ时:
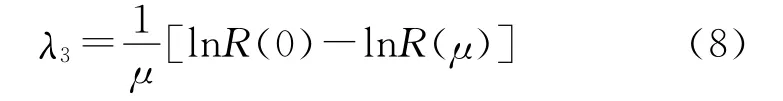
3 不同寿命分布部件并联系统备件配置优化建模
为简化计算,本文建立的并联系统备件需求预测模型假设如下:1)所有部件均为不可修件,且初始时各部件为全新件;2)不考虑环境、气候、人为因素等对部件寿命的影响;3)忽略换件时间。
假设并联系统由m个部件组成,系统各部件服从失效率为λ′i(t)(i=1,2,…,m)的不同寿命分布,通过λ-等效方法将各部件服从不同寿命分布的失效率λ′i(t)分别等效为服从λi(i=1,2,…,m)的指数分布。不同的备件配置费用不同,记为Si(i=1,2,…,m)。
在实际使用中,装备总是优先考虑完成任务的能力,在此基础上使费用消耗最低。因此,本文建模以并联系统的总费用S为目标函数,以保障度P为约束条件,寻求最优的备件配置数量,使并联系统在保障度限制条件下达到最小的费用消耗,则并联系统的数学模型为
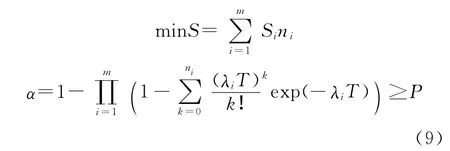
其中,ni为各部件对应的备件配置数量,λk为各部件等效为指数分布后的失效率,α为并联系统保障度。
4 运用边际效益方法优化计算备件配置数量
使用边际效益方法对并联系统的备件配置进行优化,在寻求系统保障度与备件费用之间的最佳平衡时,重复以下两个步骤直到满足保障度要求和费用限制:计算给定库存水平下的系统的保障度Ps;使用边际效益方法确定各部件对应备件的购置顺序,选择购置效益最高的备件作为下一步的购置对象,计算备件购置后的系统保障度。具体计算步骤如下:
步骤1 计算给定库存水平下的系统的保障度Ps。假设并联系统由m个指数型部件组成,其第i个部件的备件库存为ni,对于寿命服从参数为λi的指数分布的部件,其系统保障度由式(9)求得。
步骤2 使用边际效益分析方法。经过步骤1,可以算出库存水平为(n1,n2,…,nm)时的系统保障度Ps,若此时的Ps未达到目标保障度P,就在原库存水平下选择某种部件增加一个备件,则有m可能,分别为(n1+1,n2,…,nm),(n1,n2+1,…,nm),…,(n1,n2,…,nm+1)。定义增长因子Ai为第i个部件库存量从ni增加到ni+1时,系统的新旧保障度与该部件单个费用的比值,其计算表达式如下
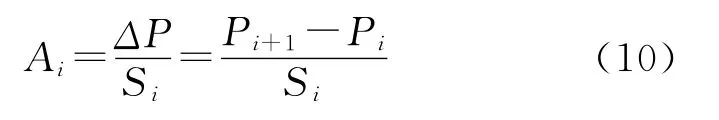
其中,Pi+1表示第i个部件增加一个备件后的系统保障度,Si表示第i个部件的单个费用。根据式(10)计算出所有部件对应的增长因子Ai,并比较出值最大的Ai,则值最大的Ai就是要增加库存的部件,其库存量增加1。把增加后的库存作为新的库存水平,重复以上步骤,直到系统保障度达到目标保障度。
步骤3 得出备件配置数量。在步骤2中,系统保障度达到目标保障度时库存水平即为备件配置数量。
5 算例分析
假设并联系统分别由如表1所示的三个部件组成,其寿命分布特征参数、单价在表中列出,初始库存为0,要求该系统在工作时间1000小时内,系统保障度达到0.97。采用近似方法和边际效益优化后得到的备件配置数量如表1所示,总费用为2.22,系统保障度为0.9972。

表1 并联系统各部件相关数据及配置数量
为验证该配置数量是否有效,利用Monte-Carlo方法进行仿真验证,仿真流程图如图1所示。通过10000次的仿真验算,在此配置方案下,该并联系统的系统保障度为0.9868,与近似计算得出的系统保障度比较接近,且达到系统保障度要求,说明近似计算方法是有效的。
6 结语
本文介绍了将非指数型部件等效为指数型部件的λ-等效方法,建立了并联系统以保障度为约束条件,以保障费用为目标的数学模型;针对由不同寿命分布类型不可修部件组成并联系统的备件配置问题,通过运用λ-等效原则,结合边际效应方法近似计算出系统各部件的备件配置数量,并通过Monte-Carlo方法进行仿真验证,证明该方法是有效的,为并联系统的配置优化问题提供了一种新思路。
[1]龙军,康锐,马麟,等.任意寿命分布的多部件系统备件配置优化算法[J].北京航空航天大学学报,2007,33(6):698-700.
[2]Willem V J,Rommert D.Spare parts stock control for redundant systems using reliability centered maintenance data[J].Reliability Engineering &System Safety,2011,96(11):1576-1586.
[3]丁定浩.备件保障性的综合与分配模型[J].电子产品可靠性与环境试验,2006,24(2):1-6.
[4]刘喜春,郑华,等.备件配置优化问题研究[J].系统工程与电子技术,2008,30(10):1934-1937.
[5]刘天华,张志华,等.weibull型多部件备件需求量的改进算法[J].海军工程大学学报,2012,24(4):41-45.
[6]陶小创,郭霖瀚,肖波平,等.基于备件保障概率分配的备件需求量预测模型[J].兵工学报,2012,33(8):975-979.
[7]Karin S S D,Nicole P E,Ana I B,et al.A spare parts model with cold-standby redundancy on system level[J].Computers & Operations Research,2011,38(7):985-991.
[8]刘天华,张志华,梁胜杰,等.一种Weibull型备件需求量的改进算法[J].系统工程理论与实践,2012,32(5):1124-1128.
[9]冯玉姣.串联系统的备件配置方法[J].电子产品可靠性与环境试验,2012,30(5):28-33.
[10]刘天华.舰船装备备件需求确定与配置优化方法研究[D].武汉:海军工程大学,2012.

