非高斯随机振动的模拟方法

徐 飞 李传日 姜同敏 荣双龙

(北京航空航天大学 可靠性与系统工程学院，北京100191)

随机振动实验的目标之一是使得产品发生累积疲劳失效，以尽早暴露产品的潜在缺陷.一直以来，随机振动台都是利用功率谱密度(PSD，Power Spectral Density)来模拟真实的随机振动环境.然而功率谱密度不包含相位信息，随机振动控制器在利用反傅里叶变换将功率谱密度转换为时域信号时，隐含的假设是各频率分量的相位服从0～2π的均匀分布.这样的假设导致生成的时域信号服从高斯分布.事实上，相位的分布和信号的概率密度函数(PDF，Probability Density Function)有关，只有当给定的随机过程是平稳的且服从高斯分布时，功率谱密度才能完全描述该随机过程.这意味着当实测信号服从非高斯分布时，只考虑了功率谱密度的随机振动台无法准确模拟实际振动环境.这样的情况一直没有得到改善，直到Vibration Research公司在2005年推出了一款能够控制峭度的商业软件［1］.该软件可以在随机振动台上生成和实测数据具有相同功率谱密度和峭度的振动信号，因此能够更好地模拟非高斯振动.典型的非高斯振动常常发生在路面运输中.Connon和Charles指出，车辆在恶劣地形上行驶时，施加在车辆上的随机激励常常是非高斯分布的，振动应力的分布情况与高斯分布情况相比，其尾部更长，且出现高峰值(如高加速度)的概率更大［2-3］.高斯信号的幅值超过3σ的时间只有0.27%，而实测信号超过3σ的时间可能达到1.5%［1］.这样的差别可能导致完全不同的累积疲劳损伤，因为大部分疲劳损伤是由2σ～4σ内的加速度引起的［4］.当实际振动环境中存在大于3σ的峰值时，会使产品在比实验室模拟更短的时间内失效.美军标810F指出，必须检查实测数据是否为非高斯信号，确保实验硬件和软件适用于非高斯信号的分析［5］.

非高斯振动的实现方法之一是波形再现法.该方法的基本思想是在实验室重复生成和某一组实测数据一模一样的信号，该方法适用于很多实验.但学者们指出，由于该方法只是生成和实测数据相同的信号，因此无法描述现场数据的可变性.例如，在现场跑车时每一圈的测试信号是不同的，如果仅仅测试一圈数据并不断重复该组数据，则无法模拟该类型跑道的真实情况.此外，美军标810F指出波形再现法通常用于控制瞬态信号或持续时间很短的随机振动［5］.该方法目前也很少被用来制定实验标准.

鉴于波形再现法存在上述缺陷，许多学者提出了其他模拟非高斯振动的方法.这些方法基本可以分为两类:①适用于模拟RMS不随时间变化的非高斯振动的方法;②适用于模拟RMS随时间变化的非高斯振动的方法.对于第1类方法，Smallwood提出了利用3种零记忆非线性函数将高斯振动转换为非高斯振动的方法［6-7］.利用这些函数生成的信号的分布略有不同，且这些方法都分别只适用于一定范围的偏度和峭度.起初，零记忆非线性函数转换法只能用于实验前生成一组非高斯信号，然而结合波形再现法在振动台上实现，之后被修正为可以实现闭环频域控制的方法［8-10］.该类方法的缺点是很大程度上减小了随机振动控制器的动态范围，从而可能破坏功率谱密度.Steinwolf提出了一种修改特定频率分量相位的算法来生成具有指定峭度的非高斯振动［8-11］，该方法不存在上述缺点.由于未改变频率分量的幅值，因此保证了功率谱密度不变.又因为相位的改变对功率谱密度无影响，从而实现了功率谱密度和峭度的独立控制.对于第2类方法，Rouillard等人提出了一种将非高斯振动分解为一系列独立的具有不同标准差和持续时间的高斯振动的方法来模拟非高斯振动［12-17］.国内也开展了相关的非高斯随机过程的模拟研究.蒋瑜等人提出了基于幅值调制和相位重构的非高斯随机振动模拟方法［18］.李锦华等人［19］基于 Johnson 转换系统和数字滤波理论，提出一种能生成指定偏度、峭度和非高斯脉动风压的方法.

本文首先结合案例给出了利用Hermite多项式法模拟RMS不随时间变化的非高斯振动的过程，并分析了该方法的适用范围.然后提出了一种新方法来模拟RMS随时间变化的非高斯振动，并结合实测振动信号对提出的方法进行了验证.

1 非高斯振动

一个均值为零的各态历经的高斯信号，其概率密度函数为

由此可见，均值为零的高斯过程可完全由其功率谱密度描述.确定一个随机过程是否可以用高斯过程来近似的一种有效方法是计算该随机过程的高阶矩，计算公式如下:

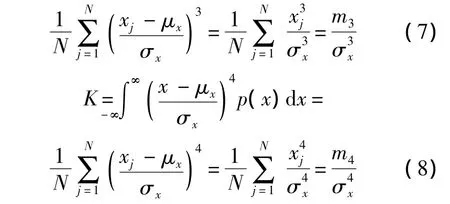
式中，S为偏度;K为峭度.

对于一个高斯过程，其偏度S=0，峭度K=3.任何偏度不为0或峭度不为3的随机过程为非高斯过程.从模拟非高斯振动的角度来看，峭度相比偏度是更重要的参数.因为峭度能够表明时域信号峰值的概率大小，利用该值可以使得实验室模拟数据的概率密度函数更接近实测数据.峭度描述了概率密度函数中间部分的尖锐度或平滑度以及概率密度函数尾部的窄度或宽度.实测振动的峭度常常是大于3的［14］.峭度大于3表明实测信号的概率密度函数的中间部分比具有相同标准差的高斯信号的概率密度函数要尖锐，且尾部更宽.更宽的尾部则意味着实测时域信号中发生高峰值的可能性比用高斯信号预测的可能性更大.而更大的峰值则会给产品带来更大的疲劳损伤和更快的疲劳失效.因此本文研究的是峭度大于3的振动信号.

2 案例分析

本文通过两个案例分别对RMS不随时间变化和随时间变化的非高斯随机振动进行了模拟方法研究.案例1利用Hermite多项式法对高斯信号进行了转换，在保证功率谱密度不变的同时得到了具有指定峭度的RMS不随时间变化的非高斯信号.案例2利用一种新方法对实测的RMS随时间变化的非高斯振动进行了模拟，模拟后得到的非高斯信号和实测信号具有相同的功率谱密度、峭度以及概率分布.

2.1 案例1:RMS不随时间变化的非高斯振动模拟

利用MATLAB生成平稳的服从标准正态分布的高斯信号，采样频率为2 kHz，采样点为100000，并假设生成的信号为加速度信号，如图1所示.

Winterstein［20］首次提出了利用 Hermite 多项式将一个平稳高斯信号x转换成平稳非高斯信号y:

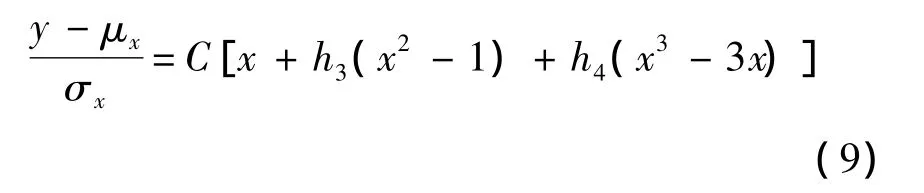
式中，h3和 h4分别是第三阶和第四阶 Hermite矩;C为缩放系数.

当给定S和K后(假设输入的S=0，K=4)，即可利用式(9)～式(12)将原高斯信号转换成非高斯信号，如图2所示.

图1 高斯振动信号Fig.1 Gaussian signal

图2 高斯和转换后的非高斯振动信号Fig.2 Gaussian and synthesized non-Gaussian signal

由于信号具有随机性，利用MATLAB生成100组独立的服从标准正态分布的信号，并分别计算转换后的非高斯信号的峭度，结果如图3所示，其均值为4.041 2，与想要得到的信号的峭度非常接近(K=4).

利用pwelch方法(采用256点的汉宁窗)求解任意一组转换前的高斯信号和转换后的非高斯信号的功率谱密度和概率密度函数，结果分别如图4和图5所示.由上述分析可知，利用Hermite多项式法可在保证功率谱密度不变的同时得到具有指定峭度的非高斯信号.但是该方法对于输入的峭度具有一定的限制.现输入不同的峭度值并计算转换后的非高斯信号的峭度值(每个输入的峭度下计算100组独立信号求输出信号的峭度均值)，结果如图6所示.

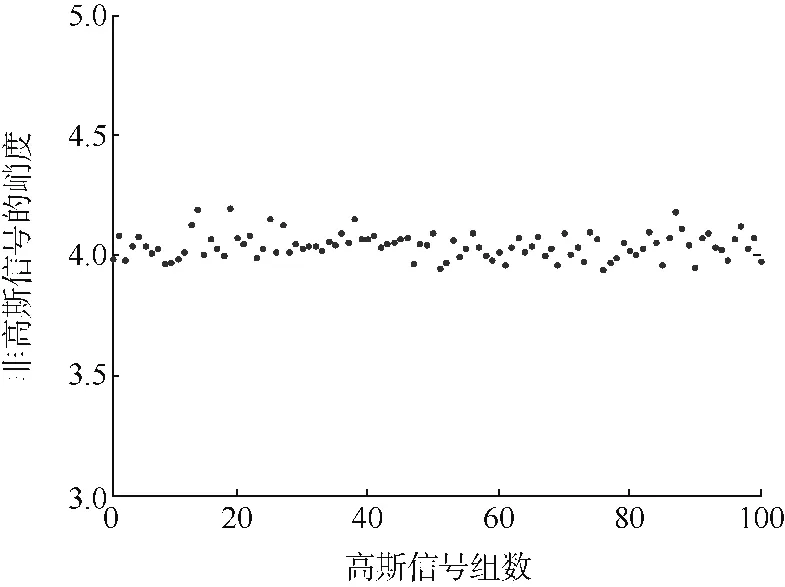
图3 100组转换后的非高斯信号的峭度Fig.3 Kurtosis for 100 synthesized non-Gaussian signal

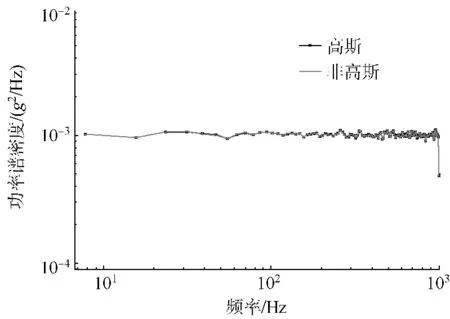
图4 高斯和非高斯信号的功率谱密度Fig.4 PSD of Gaussian and non-Gaussian signal

图5 高斯和非高斯信号的概率密度函数Fig.5 PDF of Gaussian and non-Gaussian signal

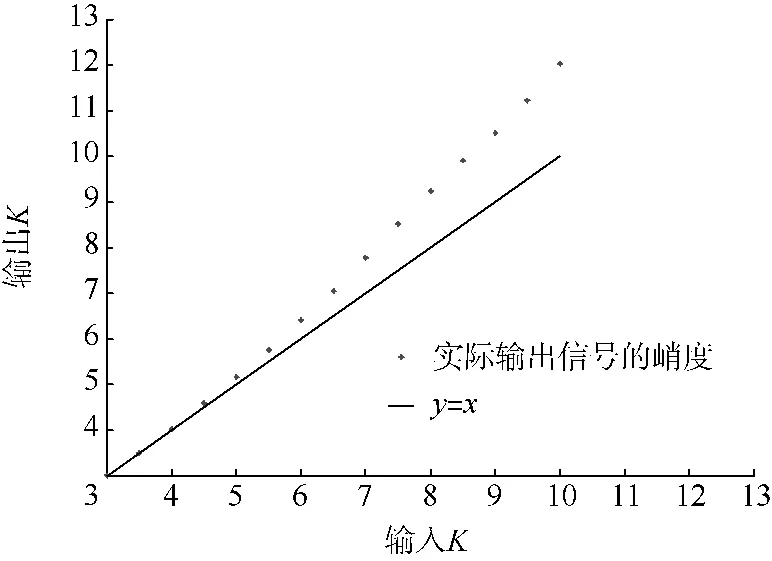
图6 输入不同峭度下得到的实际信号的峭度Fig.6 Real kurtosis calculated from given kurtosis

由图6可知，当输入峭度大于10时，Hermite多项式法的相对误差达到了20%.

2.2 案例2:RMS随时间变化的非高斯振动模拟

某段实测加速度信号如图7所示，该信号来自于爱立信公司的某个天线杆振动测试项目，测试对象如图8所示.

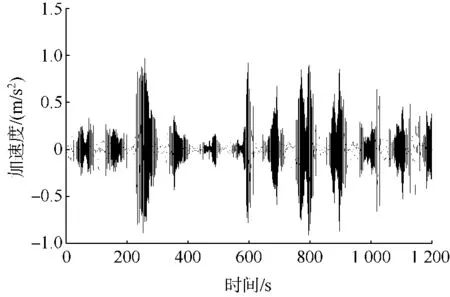
图7 实测加速度随机振动信号Fig.7 Field acceleration random signal

图8 实验对象和实验装置Fig.8 Test item and setup

经计算，该实测信号是峭度为9.426 2的RMS随时间变化的非高斯信号，传统的随机振动台无法准确模拟.本文提出一种新方法来合成这样的非高斯信号.该方法首先计算实测信号的功率谱密度，然后利用该功率谱密度生成平稳的高斯信号，最后利用实测信号的RMS的分布函数构造一个幅值调制信号与合成的高斯信号相乘，从而得到和实测信号具有相同功率谱密度、峭度和概率密度函数的非高斯信号.

利用pwelch方法(采用4096点的汉宁窗)计算该非高斯信号的功率谱密度，结果如图9所示.

图9 实测信号及合成的高斯信号的功率谱密度Fig.9 PSD of field data and synthesized Gaussian signal

对原实测信号的功率谱密度进行平滑处理(如图9所示)，再利用平滑处理后的功率谱密度生成高斯信号，结果如图10所示.合成的高斯信号的功率谱密度如图9所示.其概率密度函数和具有相同均值和方差的高斯信号的概率密度函数如图11所示.

计算原时域信号的均方根值，均方根值随时间的变化情况如图12中黑线所示，其概率密度函数如图13所示.

图10 利用功率谱密度合成的高斯信号Fig.10 Synthesized Gaussian signal from PSD

图11 实测信号及合成高斯信号的概率密度函数Fig.11 PDF of field data and synthesized Gaussian signal

图12 时域信号和均方根值Fig.12 Time history and running RMS

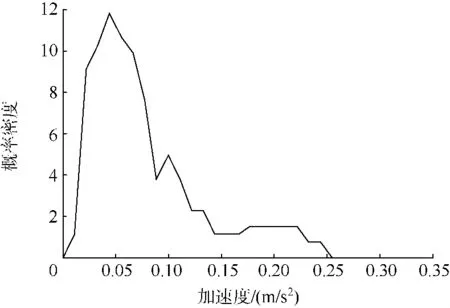
图13 RMS的概率密度函数Fig.13 PDF of running RMS

幅值调制信号由跟均方根值服从相同分布的信号构成，利用该调制信号将合成的高斯信号转换为非高斯信号.原实测信号及合成的非高斯信号如图14所示.对比实测信号及合成的非高斯信号的功率谱密度和概率密度，结果分别如图15和图16所示.由图15可知，转换后的非高斯信号保持功率谱密度和RMS不变.由图16可知，转换后的非高斯信号保持概率密度函数和实测信号一致.

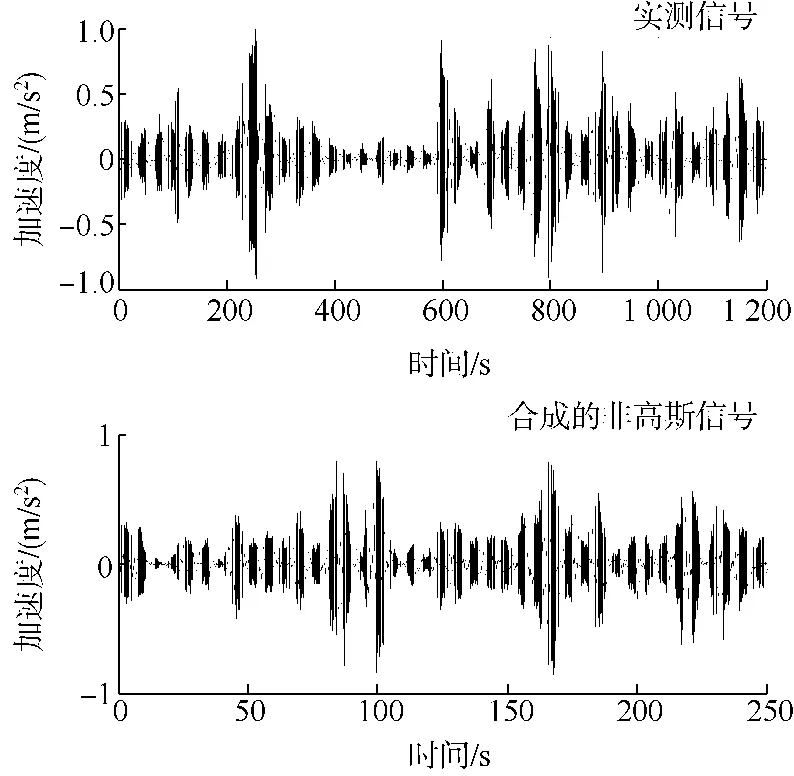
图14 实测信号及合成的非高斯信号Fig.14 Field data and synthesized non-Gaussian signal

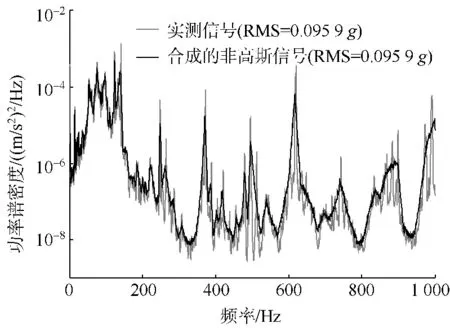
图15 实测信号及合成的非高斯信号的功率谱密度Fig.15 PSD of field data and synthesized non-Gaussian signal

图16 实测信号及合成的高斯和非高斯信号的概率密度函数Fig.16 PDF of field data，synthesized Gaussian and non-Gaussian signal

3 结论

1)Hermite多项式法可以在保证功率谱密度不变的同时得到具有指定峭度的RMS不随时间变化的非高斯信号，但该方法对于输入的峭度有限制:当输入峭度大于10时，误差达到了20%.

2)提出的新方法利用实测信号的RMS的分布函数构造一个幅值调制信号与利用功率谱密度合成的高斯信号相乘，可以得到和实测信号具有相同PSD、峭度和概率密度函数的非高斯信号.

References)

［1］ Van B P.The missing knob on your random vibration controller［J］.Sound and Vibration，2005，39(10):10-16

［2］ Connon W H.Comments on kurtosis of military vehicle vibration data［J］.Journal of the IES，1991，34(6):38-41

［3］ Charles D.Derivation of environment descriptions and test severities from measured road transportation data［J］.Journal of the IES，1993，36(1):37-42

［4］ Lambert R G.Fatigue life prediction for various random stress peak distributions［J］.Shock and Vibration Bulletin，1982:1-10

［5］ MIL-STD-810F Department of defense test method standard for environmental engineering considerations and laboratory tests［S］

［6］ Smallwood D O.Generation of stationary non-Gaussian time histories with a specified cross-spectral density［J］.Shock and Vibration，1997，4(5/6):361-377

［7］ Smallwood D O.Generating non-Gaussian vibration for testing purposes［J］.Sound and Vibration，2005，39(10):18-23

［8］ Steinwolf A.Closed-loop shaker simulation of non-Gaussian random vibrations-part 1:discussion and methods［J］.Test Engineering and Management，2006，68(3):10-13

［9］ Steinwolf A.Closed-loop shaker simulation of non-Gaussian random vibrations-part 2:numerical and experimental results［J］.Test Engineering and Management，2006，68(5):14-19

［10］ Steinwolf A.Random vibration testing beyond PSD limitations［J］.Sound and Vibration，2006，40(9):12-21

［11］ Steinwolf A.Shaker simulation of random vibrations with a high kurtosis value［J］.Journal of the Institute of Environmental Sciences，1997，40(3):33-43

［12］ Rouillard V.On the synthesis of non-Gaussian road vehicle vibrations［D］.Melbourne:Monash University，2007

［13］ Rouillard V，Lamb M.On the effects of sampling parameters when surveying distribution vibrations［J］.Packaging Technology and Science，2008，431(8):467-477

［14］ Rouillard V，Sek M A.Synthesizing non-stationary，non-Gaussian random vibrations［J］.Packaging Technology and Science，2010，23(8):423-439

［15］ Garcia-Romeu M A，Rouillard V.On the statistical distribution of road vehicle vibrations［J］.Journal of Packaging Technology and Science，2011，24(8):451-467

［16］ Rouillard V，Sek M.Creating transport vibration simulation profiles from vehicle and road characteristics［J］.Packaging Technology and Science，2013，26(2):82-95

［17］ Rouillard V.Quantifying the non-stationarity of vehicle vibrations with the run test［J］.Packaging Technology and Science，2013，27(3):203-219

［18］蒋瑜，陶俊勇，王得志，等.一种新的非高斯随机振动数值模拟方法［J］.振动与冲击，2012，31(19):169-173 Jiang Yu，Tao Junyong，Wang Dezhi，et al.A novel approach for numerical simulation of a non-Gaussian random vibration［J］.Vibration and Shock，2012，31(19):169-173(in Chinese)

［19］李锦华，李春祥，申建红.非高斯脉动风压的模拟研究［J］.振动与冲击，2009，28(9):6-9 Li Jinhua，Li Chunxiang，Shen Jianghong.Simulation of non-Gaussian fluctuating wind pressure［J］.Vibration and Shock，2009，28(9):6-9(in Chinese)

［20］ Winterstein S R.Nonlinear vibration models for extremes and fatigue［J］.Journal of Engineering Mechanics，1988，114(10):1769-1787