成败型系统可靠性增长的Bayes评估

袁 昆 李晓钢

(北京航空航天大学 可靠性与系统工程学院，北京100191)

产品研制，特别是大型复杂产品的研制过程中，在产品可靠性和性能指标没有达到预定目标之前，通常会反复经历试验—分析—改进—再试验的过程，以改进暴露出来的缺陷和增强可靠性.由于改进措施的引进，使得产品可靠性从总体上不再服从同一分布，而是呈现动态增加的趋势.在产品设计定型前要求可靠度必须达到门限值，而实际情况不允许有大样本提供，因此Bayes理论结合现场试验数据的方法多被用来实现最终阶段的可靠性评估.

在产品确定定型前，往往会进行可靠性增长试验，以验证产品可靠性是否满足要求.而如何利用可靠性增长试验评估可靠性，目前提出的主要的可靠性增长模型主要包括 Smith模型［1］、Barlow-Scheuer模型［2］、Logistic 模型［3］、折合因子法［4］等.这些模型往往基于无信息先验分布或者对各阶段增长试验信息进行折合，能给出当前试验阶段结束时的可靠性估计，但无法给出产品的最终可靠性.McLaren［5］将当前阶段的试验数据与之前阶段的试验数据、纠正措施结合起来，提出了一种迭代过程，并采用均方误差来评价模型的优劣.Nicholls等人［6］在假设成败型产品总失效个数服从泊松分布的基础上，认为各阶段失效发生概率服从Dirichlet分布，推导出可靠度的Bayes估计.为克服以往Bayes分析模型的缺点，Mazzuchi和Soyer［7］提出了基于次序 Dirichlet先验分布的可靠性增长模型，利用次序Dirichlet分布的边缘分布和联合分布能够很好地结合专家经验和相似产品的数据信息的特性，对产品各阶段可靠性进行评估和预测.刘飞等人［8］将次序Dirichlet先验分布的Bayes分析方法应用到指数型产品的可靠性增长分析，并采用Gibbs抽样得到Bayes区间估计.然而Li等人［9］指出次序Dirichlet分布在可靠性增长评估中的缺陷，并提出了基于新Dirichlet先验分布的Bayes可靠性增长模型来避免这种缺陷，在每个增长评估阶段都分别使用两个参数描述阶段可靠性的估计值和对估计值的确信程度.明志茂等人［10］基于新 Dirichlet先验分布，利用Gibbs抽样给出了多阶段可靠性评估模型，并提出利用专家经验估计和最优化方法给出先验参数估计方法，但该先验分布参数估计方法的主观性比较强，健壮性不是很好.对于可靠性增长中的经典AMSAA(Army Material System Analysis Activity)模型，Zhu等人［11］提出了 DGM-AMSAA 模型评估小子样可靠性增长问题.邢云燕等人［12］利用离散AMSAA模型，由最大熵模型和矩相等的条件，给出Beta分布先验参数估计，再结合现场试验数据给出可靠度的Bayes估计，但该方法相对而言没有充分利用上一阶段的可靠性信息，并且对于离散AMSAA模型估计值的精确度影响也没有足够的讨论.

基于上述模型的优缺点，针对成败型产品多阶段可靠性增长的评估问题，本文提出了基于新Dirichlet先验分布的Bayes评估模型.新Dirichlet先验分布能够充分利用上一阶段的可靠性信息，在使用离散AMSAA模型获得下一阶段可靠性预测值为约束条件的情况下，利用最大熵模型，获得先验分布的参数估计.再结合现场试验的数据，利用Bayes方法给出试验之后的可靠性分析与评估.该方法能够避免离散AMSAA模型的估计后验可靠性的粗糙性，相较于基于Beta先验分布和凭借专家经验获得的参数估计，分布的最大熵模型更能考虑阶段可靠性信息的运用，摒去主观性对参数估计的影响，得到的结果更准确合理.

1 可靠性增长模型

新产品在研制过程中，由于设计上的潜在缺陷，必然反复地经历试验—改进过程，以提高产品的可靠性，此过程称为可靠性增长试验(RGT，Reliability Growth Test).设RGT过程有m个阶段，每阶段试验产品数为 n1，n2，…，nm，相对应的失效次数为 f1，f2，…，fm.每阶段试验结束后，对故障进行修正改进，使得在新一阶段的产品可靠性不断增加.令第k阶段的可靠度为Rk，则各阶段的可靠度存在以下序化关系:

Bayes方法评估产品可靠性重要在于先验分布的确定和参数的估计.文献［7］中采用次序Dirichlet作为先验分布，能较好地描述专家信息，但只用一个参数描述所有阶段的方差却并不合适.因此，Li等人［9］从一般的 Beta分布出发，提出用条件分布的形式描述可靠性增长.在第k阶段未试验前，构造(Rk-1，1)上的截尾Beta分布作为该检测区间内产品可靠度的分布，称为新Dirichlet分布，即有

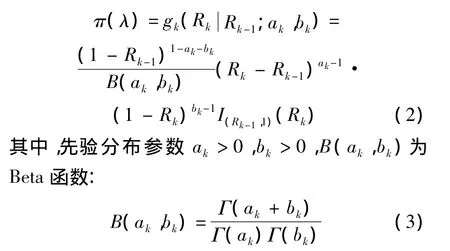
新Dirichlet分布构建在(Rk-1，1)之间，充分利用上一阶段的可靠性评估结果，每个阶段分别采用两个参数，相较于次序Dirichlet分布使用一个参数来说，更能准确地描述专家经验信息，以及体现各个不同阶段可靠性增长的变化，有更强的确信度.新Dirichlet分布在性质与(0，1)上的标准Beta分布性质类似.

在给定的Rk-1的条件下，求得Rk的均值和方差为

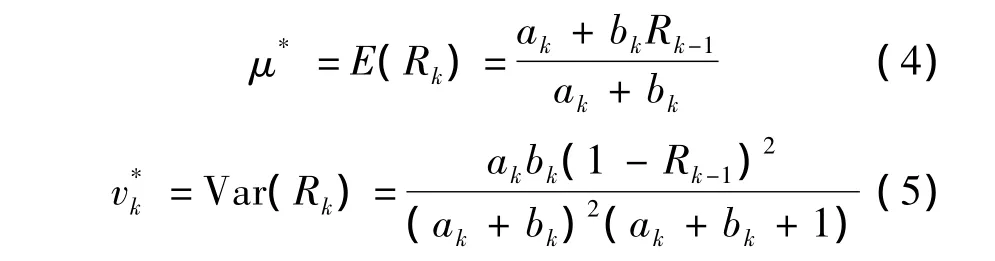
新Dirichlet先验分布的后验均值相较于Beta分布，增加了前一阶段可靠度Rk-1的影响.若对Rk-1的大小进行变通，则其取值大小反映了对当前可靠度估计值的不确定性和下一阶段可靠度的预测，具有专家经验的指导意义.从新Dirichlet分布的特征来看，相对于次序Dirichlet分布，新的先验分布的期望和方差的物理意义不是很明显.若要应用新Dirichlet先验分布于可靠性增长的Bayes评估问题，必须先获得先验分布的参数估计.

2 新Dirichlet先验分布的参数确定

文献［10］利用专家经验给出每一阶段可靠度估计值取值的区间范围，再最优化与均值和方差相关的函数来获得先验参数.然而该方法中专家经验给出区间均值和方差的不同会导致不同的参数估计，主观性对参数估计的结果影响较大，因此，为能够摒弃主观性对于参数估计的影响，采用基于最大熵原理的参数估计方法来获得先验分布参数估计.在信息论中，熵是不确定性的一种度量［13］.在无信息或信息很少的情况下，用最大熵来确定先验分布，就是采取一种保守的方法.新Dirichlet先验分布已经充分包含之前有的可靠性信息，因此基于最大熵原理的参数估计方法是可信的.

先验分布π(Rk)的熵可以表示为

若要求得先验分布的参数估计，必须给出关于下一阶段可靠性Rk的相关信息，例如均值或者分位值等信息.本文假设在给出关于Rk的期望均值估计的条件下，通过极大化下列模型得到参数估计:

由于新Dirichlet分布的形式比较复杂，可借助计算软件搜索最大熵的估计值.对于下一阶段可靠性的估计R^k，可以通过专家经验给出，为了减少主观性对参数估计的影响，本文采用离散AMSAA模型求得可靠性估计值R^k.

3 离散AMSAA模型

文献［14］在对各种产品的失效数据进行统计分析时，提出一个近似函数关系式来描述失效数据与失效时间之间的关系，即学习曲线特性:其中，λ为该函数形状参数，β为尺寸参数，均为正值;T为累计的试验时间;函数K(T)表示到时间T时观测到的累计失效次数.

如果将式(8)中的累计试验时间T改为累计试验次数N，使其离散化，便可以得到离散型学习曲线特性［15］:

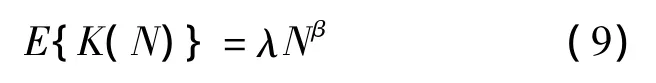
则每一试验阶段失效次数为

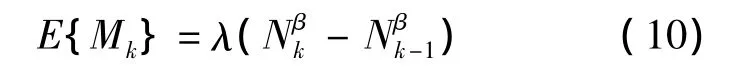
如此，每一阶段的可靠度为

其中，nk=Nk-Nk-1，表示第k阶段的试验样本数;λ为初始阶段可靠性，0＜λ＜1;1-β为增长率，0＜β＜1.

模型假设改正措施是在试验结束之后进行，并且试验中发生失败次数为随机数.

对于模型中的参数求解，可借助于极大似然函数获得:

其中，fk表示在第k阶段失效次数;n表示试验的阶段数.

已知第k阶段的试验样本量nk，利用式(12)得到参数估计值和，则第k阶段的可靠性估计值为

4 可靠性Bayes估计

设在第k阶段的可靠性现场试验中，试验数据为(nk，fk)，则现场试验数据的似然函数为

其中，nk为试验次数;fk为试验中失败次数.

先验分布的参数估计通过AMSAA模型和最大熵模型得到.由于新Dirichlet分布的性质与Beta分布的性质相似，那么根据Bayes原理，结合现场试验数据得到可靠性后验分布为

5 实例分析

某成败型产品研制试验采用延缓纠正方式，已经历4阶段的可靠性试验.其中，第1阶段试验4次，失败2次;第2阶段试验5次，失败2次;第3阶段试验5次，失败1次;第4阶段试验4次，全部成功.根据上述试验数据，分析此时试验结束时的产品可靠性是否满足要求(可靠度为0.9).

根据已有的4阶段试验信息，基于Laplace检验统计量进行可靠性增长趋势检验.结果表明当显著性α=0.2时，μ=-1.3771＜μα=1.282，可靠性有明显的增长趋势.由式(12)，得到离散AMSAA模型参数的极大似然估计，=0.988 4，β^=0.5588.根据式(13)得到第3阶段可靠度估计=0.811，第4 阶段可靠度估计=0.837.然而，根据第3阶段和第4阶段的试验信息，可以粗略判断后验可靠度至少在90%以上，显而易见离散AMSAA模型对于下一阶段可靠度的估计精度并不十分准确.本文采用基于新Dirichlet先验分布的Bayes方法估计试验结束后的可靠性.

将AMSAA模型估计得到的第3阶段可靠性作为起点，在区间(Rk-1，1)上构建新Dirichlet先验分布.以第4阶段可靠性估计值作为均值约束，利用式(7)的最大熵模型获得参数的估计.然而由于两阶段可靠性估计值相近，导致最大熵模型求解先验参数无解.由于离散AMSAA模型对下一阶段参数估计的不准确，为了校正模型故取0.9Rk-1代替 Rk-1，由式(16)得到最终可靠度的Bayes后验期望为=0.938，可信度为90%时对应的可信下限R0.9=0.7424.

从离散AMSAA模型在给出下一阶段的可靠度估计值上看，仅凭离散AMSAA模型估计后验可靠性可能会存在明显误差.如果对离散AMSAA模型获得的下一阶段可靠度估计值的区间范围存在准确度的疑虑，从而导致在区间(Rk-1，1)上给出的可靠度后验估计值增大的情况，可以选取一个校正系数c∈(0，1)，作为对估计值R^k-1的信任度，c越趋近于1表明对R^k-1估计值的确信度越大，从而用(cRk-1，1)代替(Rk-1，1)进行该阶段的新Dirichlet先验分布的构建.由式(16)可知，该阶段的后验期望有随着c减小而减小的趋势，说明c的大小也是对最终后验可靠度估计值的确信度大小的表示，c越小表明对后验估计得越趋向于保守.表1列出了不同c值时该阶段的后验可靠度的估计值.从结果分析上看，当c的取值低于某一值时，该阶段的先验参数b的估计值相同，变化的是先验参数a的值，经过大量仿真试验也发现类似情况，导致上一阶段可靠度估计对后验可靠度估计影响减弱，估计结果趋向于Beta分布估计，证明了常数 c在可靠性估计中的作用.新Dirichlet先验分布的估计结果与Beta先验分布相比较，Beta先验分布略显保守，是因为没有充分利用每一阶段的可靠度信息，因此更能突出新Dirichlet先验分布的优势.

表1 不同c值对应的可靠度后验估计Table 1 Reliability posterior estimation corresponding to different value of c

然而通常离散AMSAA模型对当前可靠度的估计准确度还是比较可信的，但若得到的下一阶段可靠度估计值明显不准确，则需要根据专家经验对可靠度估计值进行修正.表2列出了对下一阶段可靠度估计值进行修正后的后验可靠度的变化.从表2结果对比中可以看出，给出先验信息越高时，获得的后验估计也就越大，因此对于先验信息的修正也反映出专家经验对于产品可靠度的判断.从两表对比可以看出，对于下一阶段可靠度估计值的修正对后验可靠度的影响，要大于对上一阶段可靠度估计区间修正的影响.适当利用专家经验，可以使得评估结果更优.

表2 不同先验信息对后验可靠度的影响Table 2 Impact of different prior information on the posterior reliability estimation

从表1、表2的评估结果分析可以看出，在离散AMSAA模型给出的可靠度估计不甚理想时，如当利用离散AMSAA模型估计得到的下一阶段可靠度的估计值与当前阶段估计值相近时，或者离散AMSAA模型对当前阶段和下一阶段的可靠性估计同时出现误差较大时，可能会导致利用最大熵模型时不能获得先验参数估计.此时后验可靠度的大小可以通过专家经验对于下一阶段可靠度估计的准确性和取值范围的确信度的判断对模型进行修正.因此，基于新Dirichlet先验分布的Bayes估计方法能够较好地融合专家经验和上一阶段的可靠度信息，比单纯运用离散AMSAA模型估计下一阶段可靠性要准确得多.

6 结论

1)针对成败型系统的可靠性增长问题，在结合离散 AMSAA模型的基础上，提出了基于新Dirichlet先验分布的评估模型.该模型能够充分利用各阶段的可靠性信息，在合适的专家经验指导下，能够较为准确地得到系统增长后的可靠性.

2)该模型评估系统增长后的可靠性的精度与专家经验有关，在对当前阶段的可靠度无法给出恰当的估计时，该模型可以退化成Beta分布，具有一定的灵活性.

3)相较于传统模型中采用的积分模型，该模型的计算过程较为简便，避免复杂的积分问题，能够保证计算结果的准确性.

然而，该模型还存在一些问题.

1)当离散AMSAA模型对上一阶段可靠性的估计存在明显偏差时，利用校正系数进行校正时，该系数选取值的大小存在主观性.如何给出校正系数客观公正的选取规则，是需要研究的问题.

2)上一阶段可靠性估计不准确也可能会导致利用最大熵模型得不到先验分布的参数，此时同样需要借助校正系数进行改进.在选取校正系数时，也需要同时考虑极大熵模型的影响.

References)

［1］ Smith A F M.A Bayesian note on reliability growth during a development testing program［J］.IEEE Transactions on Reliability，1977，R-26(5):346-347

［2］ Barlow R E，Scheuer E M.Reliability growth during a development testing program［J］.Technometrics，1966(8):53-60

［3］ Sohn S Y.Bayesian dynamic forecasting for attribute reliability［J］.Computer＆ Industrial Engineering，1997，33(3/4):741-744

［4］田国梁.二项分布的可靠性增长模型［J］.宇航学报，1992(1):55-61 Tian Guoliang.Reliability growth models for binomial distribution［J］.Journal of Astronautics，1992(1):55-61(in Chinese)

［5］ McLaren A E.A method for reliability growth analysis combined over multiple stages［D］.West Lafayette:Purdue University，2011

［6］ Nicholls J L.Reliability growth of multi-stage single shot systems［D］.Washington D C:The George Washington University，2011

［7］ Mazzuchi T A，Soyer R.A Bayesian attribute reliability growth model［C］//Proceedings of the Annual Reliability and Maintainability Symposium.Piscataway，NJ:IEEE，1991:322-325

［8］刘飞，王中伟，张为华.指数寿命产品可靠性增长试验的Bayes分析［J］.国防科技大学学报，2006，28(4):128-132 Liu Fei，Wang Zhongwei，Zhang Weihua.Bayesian analysis of reliability-growth test for exponetial life distribution case［J］.Journal of National University of Defense Technology，2006，28(4):128-132(in Chinese)

［9］ Li G Y，Wu Q G，Zhao Y H.On Bayesian analysis of binomial reliability growth［J］.J Japan Statist Soc，2002，32(1):1-14

［10］明志茂，张云安，陶俊勇，等.基于新Dirichlet先验分布的指数寿命型产品多阶段可靠性增长Bayes分析［J］.兵工学报，2009，20(6):733-739 Ming Zhimao，Zhang Yun'an，Tao Junyong，et al.Multi-stage reliability growth bayes analysis for exponential product based on new Dirichlet prior distribution［J］.Journal of Acta Armamentarii，2009，20(6):733-739(in Chinese)

［11］ Zhu X，Fang Z.“DGM-AMSAA”model of reliability growth based on the small sample［C］//2013 IEEE International Conference on Grey Systems and Intelligent Services.Piscataway，NJ:IEEE，2013:123-126

［12］邢云燕，武小悦.成败型系统可靠性增长的动态Bayes评定方法［J］.系统工程理论与实践，2010(4):695-699 Xing Yunyan，Wu Xiaoyue.Dynamic Bayesian evaluation method for binomial system with reliability growth［J］.Journal of Systems Engineering-theory ＆ Practice，2010(4):695-699(in Chinese)

［13］ Berger J O.Statistical decision theory and Bayesian analysis［M］.Heidelberger:Springer，1985

［14］ Fries A，Sen A.A survey of discrete reliability-growth models［J］.IEEE Transactions on Reliability，1996，45(4):582-604

［15］ Fries A.Discrete reliability-growth models based on a learningcurve property［J］.IEEE Transactions on Reliability，1993，42(2):303-306