钨合金力学性能表征分子动力学模拟

于超，任会兰，宁建国

（北京理工大学 爆炸科学与技术国家重点实验室，北京100081）

近几十年，随着科学技术高速发展，尤其航空航天、兵器、计算机、核能和船舶等工业领域对材料的性能要求越来越高，而纳米技术能使常规材料呈现出非常规物理特性，决定了纳米材料和纳米结构将成为当今新材料研究领域中最富有活力、对未来经济和社会发展有着十分重要影响的研究对象，也是纳米科技中最为活跃、最接近应用的重要组成部分［1，2］。对新材料的创新起着至关重要作用，致使纳米科技得到了更广泛的关注与研究，具有巨大的市场价值和开发价值。

钨和钨合金具有高强度、高密度，良好的抗腐蚀性、导电、导热性和热膨胀系数小等一系列优良物理、力学性能。在军事领域中，如：卫星、飞行器、航空发动机、核潜艇、导弹和舰艇等装备的一些关键部件大量采用了钨及钨合金，它们的机构设计和安全性能问题与所采用的材料物理化学和机械特性有着十分密切的关系。

国内外许多研究学者对钨及钨合金进行了大量的宏观实验研究，Zhou等［3］采用拉伸冲击实验装置对钨合金试件在不同应变率下的工况进行了实验研究，且在对冲击拉伸后断裂试件扫描分析，建立了含有应变率相关参数的应力－应变模型。刘海燕等［4］基于旋转盘式间接杆－杆型冲击拉伸装置，对不同颗粒度细化钨合金材料在不同应变率工况进行了实验研究，通过分析钨合金材料在弹性阶段存在非线性，判断了在此阶段材料内部已经损伤、钨颗粒减小材料屈服极限提高以及细化钨合金材料具有应变率致脆现象。李娜等［5］通过实验研究了83W和89W材料各向异性在不同温度环境的动、静加载条件下，应力－应变关系及失效问题。Pink等［6，7］研究了钨合金材料在不同温度下的拉伸性能，并发现钨合金材料在一定温度下出现动态应变时效现象和负应变率敏感性问题。王世良等［8］研究了钨合金的合成以及相应的物理问题，谷怀鹏等［9］研究了镍基单晶合金物理特性问题。王建伟等［10］采用分子动力学方法研究bcc－Fe不同空位浓度对中子辐照损伤的影响。以上这些专家与学者分别对钨合金材料的实验研究、相关合金物理特性和金属材料的分子动力学模拟等方面均取得了一定的研究成果，并促进钨及其合金材料的进一步发展。

然而，利用扫描电子显微镜对钨合金材料和钨合金结构破坏观察研究分析，钨合金材料主要由钨颗粒构成，而在不同加载工况下，钨颗粒的破坏是造成钨合金整体失效的主要原因。钨颗粒的强度决定了钨合金的物理力学性能，但是由于钨的高强度、高硬度，在宏观试验中很难测得其实际的物理性能的常规参数。针对这一问题，采用分子动力学方法研究钨颗粒的材料力学性能成为了一种有效的手段，钨颗粒尺寸对宏观材料尺寸相对无限小，而对微纳米尺寸又可认为是无限大，分子动力学方法它可以根据原子间的相互作用计算整个原子系统的性能，分析材料的纳观变形机理，再现宏观力学行为，同时又提供大量的微观信息。

分子动力学模拟是一种用来计算一个经典多体体系的平衡和传递性质的方法，是指对于原子核和电子组成的多体系统，应用牛顿力学运动方程，对原子核运动过程进行模拟，记录运动过程中的轨迹，最终利用统计力学方法计算一些相关物理量，得出物质结构特性的一种理论计算方法。该模拟手段已成功应用于研究晶体熔化、晶体冲击、晶格畸变等方面［11］，并且随着计算方法的发展以及计算机性能的提高，将被广泛应用于生物、化学、医药等领域，有着广阔的应用前景。采用分子动力学方法，对钨合金的拉伸塑性问题还未展开系统研究。

利用分子动力学模拟钨合金拉伸塑性力学行为，对［100］晶向进行温度效应、尺度效应、应变率效应的模拟研究，得到了钨合金微观结构变化图像和应力应变关系等相关塑性力学数据，以及解决了在微纳米尺度材料实验中较难观测原子轨迹及提取相应数据测量的重要问题，对于进一步了解微纳米尺度钨合金材料力学性能及其材料制备与应用提供了重要的依据。

1 钨合金的拉伸模型

1.1 嵌入原子势

嵌入式原子势（EAM）是 Daw和Baskes［12］根据Hohen－kohn定理建立的势函数模型，具有运算量小、运算效率高、适合金属间的作用等优点。

EAM原子势的总能量E可以表示为：

式中：φij表示距离为rij的原子i和原子j之间的对势能；Fi表示电子密度为ρi的原子i嵌入能；Mi（Pi）为修正项；Pi为原子i处电子密度中高次项的贡献。

1.2 钨合金计算模型

图1为金属体心立方结构示意图，晶格常数为a＝b＝c＝0.3165nm［13］。图2是以体心立方结构为基础，建立钨合金圆柱形超晶胞计算模型（钨合金主体钨为体心立方结构），初始构型按理想晶格排列，x，y，z坐标轴分别对应［100］，［010］，［001］方向。圆柱半径为r＝14a，长为l＝40a，两端分别固定长度h＝2a为夹具区域，模型左端固定，右端采用“velocity”加载方式进行拉伸，共有49773个原子。为模拟有限长度的力学行为，x，y，z方向均取自由边界条件。

图1 体心立方结构示意图Fig.1 Body－centered cubic structure

图2 计算模型Fig.2 Calculation model

2 模拟方法

采用Ackland的EAM势函数［14］描述钨合金原子之间的相互作用，它能准确的拟合出钨合金结合能、缺陷形成能、层错能等参数，更能准确拟合钨合金的弹性性质。首先，本模型采用Hoover－Nose控温系统，在正则系宗（Canonical Ensemble，NVT），即表示具有确定的粒子数（N）、体积（V）、温度（T）环境下，对模型体系进行弛豫，将模型控制在一定的温度使体系达到一个初步稳定的状态。再利用微正则系宗（Microcanonical Ensemble，NVE）。即表示具有确定的粒子数（N）、体积（V）、总能量（E）对体系进一步弛豫，达到理想的加载环境。在此基础上，采取与宏观实验相类似的加载方式，对钨合金圆柱模型进行拉伸加载问题的分子动力学计算模拟。

3 钨合金体系模型弛豫

所谓模型弛豫，就是体系达到一个稳定的状态，以便获得准确的数据。图3为［100］晶向、截面半径r＝14a、长度l＝40a、温度300K下模型弛豫的动能与势能的变化情况，由图3分析可知，在Hoover－Nose控温系统下，在体系进行弛豫初始时，体系动能与势能上下波动幅度较大，此时体系并有达到平衡状态。在经过30ps的弛豫以后，体系动能在2000eV小幅波动变化，而势能在－433000eV左右小幅度周期性波动，体系基本上达到一个相对稳定的状态，可以对其进行加载计算。

图3 弛豫动能（a）和势能（b）时间曲线Fig.3 Kinetic energy curve（a）and potential energy curve（b）at different times in the relaxation

4 数值模拟与实验验证

4.1 钨合金塑性变形数值模拟研究

4.1.1 在拉伸过程中的体系结构变化

采用［100］晶向、截面半径r＝14a、长度l＝40a、初始温度300K。首先在NVT系宗下弛豫50ps，再在NVE系宗下弛豫50ps。对模型右端加载区域施加0.25nm／ps沿x轴正向速度进行拉伸，中间区域为自由运动，每步输出一次热力学信息（温度、压力、势能、总能量、x轴应力、x轴应变）共运行100000步。图4为对钨合金试件拉伸加载作用下，原子运动变化趋势（基于OVITO软件［16］对计算数据进行图形绘制）。

当0≤t＜7.5ps时，在加载速率初始阶段，钨合金为完整晶体，原子结构为规则的晶格排列，拉伸变形为弹性变形。随着晶体拉伸持续进行，原子之间产生了位错，并伴随着滑移变形，在模型表面出现轻微滑移台阶。

图4 钨合金拉伸时原子运动过程Fig.4 The movement of tungsten atoms at tensile state

当7.5≤t＜15ps时，钨合金在拉力的作用下不断伸长，发生了由弹性变形到塑性变形的转变。从图中可看出原子在（110）晶面、沿［111］晶向进行滑移，随着拉伸的进行，原子的运动越来越快，开始出现部分金属键发生断裂，当应变不断增加时，位错不断增殖，滑移持续发生，中间段横截面发生改变并不断的减小，并出现了颈缩现象。当拉伸进一步伸长时，塑性变形主要集中在颈缩部位，其他部分原子位置基本不变，颈缩区域不断伸长，导致滑移系的连续发生，颈缩区域横截面不断减小，颈缩现象更加明显，大部分金属键已发生断裂。

当15≤t＜28.5ps时，随着拉伸的进一步进行，颈缩区域原子明显减少，原子相互作用力越来越小，当金属键完全断裂，晶体发生断裂，表明纳米尺度下钨合金高应变率拉伸变形方式类似于宏观体心立方材料的拉伸变形。

4.1.2 钨合金高应变率拉伸过程变化曲线计算原子i的应力分量采用如下公式：

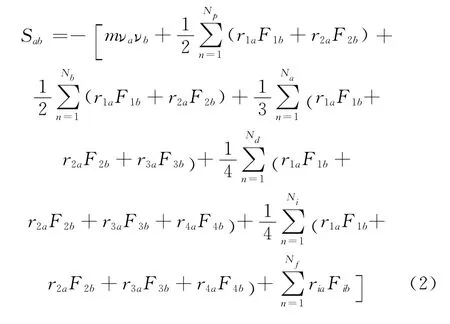
式中：m表示原子质量；a，b表示x，y，z轴对称张量的六个分量；r表示两个原子之间的距离；F表示两个原子之间的作用力。第一项表示原子i的动能，第二项是原子i周围Np近邻原子数经过n次循环的对能，第三项是原子i周围Nb的键能，第四项是原子i周围Na键角对应力的作用，第五项是原子i周围Nd面角对应力的作用，第六项是原子i周围Ni非健项对应力的作用，最后一项是原子i内部约束力Nf对应力的作用。

图5为不同工况拉伸加载下铝合金应力－应变曲线。从图5（a）可以看出，分子动力学模拟与宏观实验得到的应力－应变曲线相同的是初始为线性上升，应力与应变成正比例关系，材料为弹性变形阶段，区别是分子动力学模拟得到的弹性极限到最高点后发生突降现象，并产生塑性流动。钨合金模型随着加载速率的增加，屈服强度逐渐增大。钨合金在0.010，0.050，0.100nm／ps的高应变率加载速率拉伸过程中发生了二次屈服，而在0.001nm／ps时钨合金模型没有产生二次屈服。

在分子动力学模拟中，不同拉伸速率下的钨合金模型采用了相同的弛豫时间，因此，在较低的拉伸速率下，弛豫时间充分，钨合金可以再次达到稳定的平衡状态，而在较高的拉伸速率下，弛豫时间不足以使钨合金体系达到稳定的平衡状态。因此，在相对较高的拉伸速率下，钨合金体系会产生二次屈服，而在较低的拉伸速率下没有发生二次屈服。

图5 钨合金应力－应变曲线（a）不同应变率；（b）不同试件截面半径；（c）不同试件长度；（d）不同环境温度；（e）材料不同晶向Fig.5 Stress－strain curves of tungsten alloy（a）different tensile strain rates；（b）different radius of the cross sectional area of the specimen；（c）different length of the specimen；（d）different environmental temperatures；（e）different crystal orientation

而MD模拟弹性极限到达最高点后发生突降现象，是由于在拉伸过程中原子之间持续产生位错，进一步发生了滑移，当达到钨合金屈服应力峰值时，原子之间滑移不断加剧，引起原子之间大量金属键发生断裂，故导致“突降”问题。

从对图5（b）应力－应变曲线分析可知，钨合金模型在温度300K、长度l＝14a、［100］晶向以0.1nm／ps速率加载的条件下，随着模型横截面半径的增大，在弹性阶段钨合金的屈服强度也越大。这说明在高应变率拉伸过程中，横截面的越大，在单位时间内产生的位错密度越大，位错之间的交互作用也就越强，增加了位错运动的阻力，导致了屈服强度的提高。

由图5（c）可以看到，在温度300K、横截面半径r＝14a、［100］晶向以0.1nm／ps加载的条件下，随着钨合金模型长度的增加，钨合金在弹性阶段屈服强度在增大。从图中可以看出，不同长度钨合金模型的应力－应变曲线斜率相等，说明弹性模量与模型长度尺寸没有关系。

从对图5（d）的应力－应变分析可知，钨合金塑性变形对温度的变化具有很高的敏感性，但应力－应变变化的趋势基本相同。首先，是线性上升，为钨合金的弹性变形阶段。其次，随着应变的增加，体系进入塑性变形阶段，且体系应力呈现一定的波动性。而随着温度的上升，其屈服强度逐步下降，屈服后应力波动幅度逐渐降低，与宏观拉伸变形相似。

这是因为，随着温度升高，金属原子振动更加剧烈，从而金属键合力减小，金属发生软化现象，当温度升高到一定程度时，金属会发生一定的黏性流动，且温度越高，则黏性流动的抗力越小，其发生蠕变的范围也越大，蠕变很大程度上导致金属屈服应力等非弹性变形对应的流动应力下降，但提高了钨合金的塑性。

图5（e）表明，不同晶向的高应变率拉伸加载钨合金材料具有不同的等效弹性刚度和屈服强度，［111］晶向钨合金模型屈服强度最大，［110］晶向次之，而［100］晶向钨合金模型屈服强度最低。［100］晶向的钨合金呈现最大屈服应变，［111］与［110］晶向的屈服应变近似，可近似为［100］晶向的三分之一。晶向对力学性能的影响这一特性对于纳米材料在不同领域的应用具有极其重要的研究价值。

4.2 钨合金拉伸实验验证

4.2.1 准静态拉伸验证

实验材料选取91钨合金细化颗粒材料为对象，进行了不同工况的实验研究，wW∶mNi∶mFe＝91.0∶6.3∶2.7。它是将10.0～15.0μm的细化预合金粉末经固相烧结得到的钨含量相同晶粒度不同的细观粒状复合材料。图6为将烧结后钨合金材料（棒材）经线切割加工后成扁平哑铃型试件。在实验前需要把试件实验段的圆弧部分沿纵向研磨光滑，以减小试件拉伸段圆弧部分的应力集中现象。

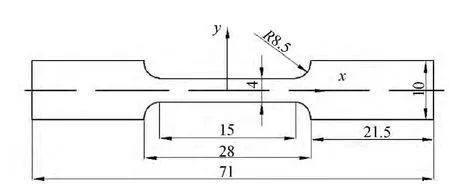
图6 拉伸试件示意图（mm）Fig.6 The schematic of the tensile specimen（mm）

图7为采用S－570扫描电子显微镜试验系统对91钨合金细化颗粒材料试件扫描后，给出的钨合金微观组织像。由图7可知，钨合金钨颗粒为半径不同，但近似球形，相对均匀的被黏结相包围。颗粒与颗粒之间的界面接触面较小，黏结相和晶粒之间的界面在所有界面中占多数，还可以看到有孔洞等微缺陷。

图7 91%钨合金材料的SEM图Fig.7 SEM image of the 91%tungsten alloy material

准静态单向拉伸实验在MTS810液压伺服材料实验机上进行，采用位移控制速率方式加载，在试件实验段安装引伸计测量应变，通过计算机输出实验结果数据文件。表1给出了不同应变率下的钨合金材料准静态屈服强度。

表1 不同应变率对应的钨合金屈服强度Table1 Yield strengths of the tungsten alloy at different strain rates

图8为91在不同应变率下，钨合金材料准静态拉伸实验的应力－应变曲线。由图8分析可知，随着拉伸应变率的增加，91钨合金材料的强度有一定的提高，具有典型的应变率强化效应；在不同的拉伸应变率加载条件下，钨合金材料应力－应变曲线主要呈现了弹性变形阶段，且材料伸长率达到0.153%时，试件发生断裂，几乎没有塑性变形，据此可以判断此颗粒度的细化钨合金材料为典型脆性材料。

对准静态91钨合金细化颗粒材料在准静态拉伸加载破坏的试件材料断口利用电镜扫描图像（见图9）。对图像观测分析，可以看到大部分钨颗粒发生解理断裂，颗粒的解理断面上是扇形花样，解理台阶为扇形的肋。扇形花样的肋线的汇合点，为解理裂纹的起源点。河流花样以扇形的方式向外扩展形成所谓的扇形花样。从钨合金材料断口处还可以观察到相邻颗粒的接触面在受外载时分开后留下的痕迹。说明钨合金材料中同样存在少量颗粒与颗粒之间的W－W界面。

图8 准静态实验拉伸的应力－应变曲线Fig.8 Stress－strain curves of the tensile experiments at quasi－static state

图9 钨合金断口的SEM图Fig.9 SEM images of the fracture surface of the tungsten alloy

从图9中钨合金材料断口的显微图像上较为光亮的部分是材料的黏结相，黏结相断口呈现纤维状，有韧窝，是韧性断裂。钨合金材料在外受载时，黏结相协调了变形并重新分配应力，使强度较高的钨颗粒承担了主要载荷；继续增大外载到一定值，钨颗粒之中产生微裂纹，裂纹扩展，钨颗粒被解理。钨颗粒的解理断裂是材料失效的主要原因。

4.2.2 动态拉伸实验

图10为旋转盘式间接杆－杆型冲击拉伸实验加载装置示意图。采用该装置对钨合金试件进行加卸载实验，其中加载装置为直径1.4m，转动线速率可以达到100m／s的飞轮。

图10 动态拉伸实验加载装置示意图Fig.10 The schematic of the loading equipment in dynamic tensile experiments

91细化钨合金材料动态拉伸实验是在室温（14℃）条件下进行的，分别在1×10－3，200s－1和500s－1三种应变率工况下进行动态拉伸实验研究，在每一工况下进行了四组实验。图11为在不同应变率条件下实验获取的钨合金材料动态拉伸的应力－应变关系曲线。

图11 动态拉伸实验的应力－应变曲线Fig.11 The stress－strain curves in the dynamic tensile experiment

对图11分析可知，不同应变率动态拉伸导致了钨合金材料应力－应变曲线有一定的差异，反映了91钨合金颗粒材料具有应变率效应，且随着加载速率的提高，屈服应力相应增加，但是由于材料自身的缺陷，导致了测量的数值具有一定波动，也降低了钨合金材料强度的下降。

为了更好地了解钨合金材料的力学性能及在高应变率下钨合金强度变化规律，采用分子动力学方法对该问题进行了模拟研究（通过研究分析模型形状对强度变化影响可以忽略）。

表2为在计算模型截面半径r＝14a、长度l＝40a、温度300K，加载方向采用［100］晶向下，不同应变率加载相对应的钨合金屈服强度数据。

表2 不同应变率对应的钨合金屈服强度Table2 The yield strengths of tungsten mono－crystal corresponding at different strain rates

通过对表2的数据进行平均差值及数据拟合得到了钨合金拉伸的应变率及屈服强度的幂律拟合公式。如下：

式中：α＝19.88023；β＝0.08598；σs为屈服强度，单位为GPa；为应变率，单位为108s－1。

图12为通过拟合的公式与钨合金的实验数据对比。对图12分析可知，低应变率拉伸加载区域拟合的较好，且相同的应变率条件下，MD模拟对应的屈服强度高于宏观实验的屈服强度，分析认为，钨合金是完美晶体没有任何缺陷，而宏观实验材料内部很可能存在微小的空洞、微裂纹以及杂质等外在的因素从而降低了钨的屈服强度。MD模拟钨合金得到的屈服强度很高，这一结论与Михаловский等［15］实验测得拉伸钨晶须的屈服强度24.75GPa近似，这说明采取的钨合金计算模型、弛豫时间、加载方式是合理的，拟合得到的幂律公式是准确的，尤其对于在实验中很难对高应变率拉伸加载测试手段获得相应的塑性力学参数，分子动力学方法显得具有更加重要实际意义。

图12 钨合金应变率与屈服强度曲线图Fig.12 Strain rate－yield strength curve of tungsten alloy

5 结论

（1）钨合金材料在相同晶向、截面尺寸、温度的条件下钨合金随着拉伸应变率增加，屈服强度升高；且高应变率下的钨合金在屈服时对应的屈服强度更大，并且容易发生二次屈服。

（2）相同晶向、截面尺寸、应变率的条件下拉伸钨合金随着温度升高，屈服强度不断降低；而相同晶向、温度、应变率的条件下拉伸钨合金截面尺寸增加，屈服强度有所增加。

（3）在相同温度、应变率、截面尺寸的条件下，晶向效应的改变对钨合金材料屈服强度和伸长率具有较大的影响。

（4）分子动力学方法可以准确预测钨合金材料在高应变率加载下应力应变关系，也可定性的说明钨合金在冲击载荷作用下，热力学参量的变化规律和发生相变的主要机理。

［1］徐云龙，赵崇军，钱秀珍.纳米材料学概论［M］.上海：华东理工大学出版社，2008.

［2］王鸿鼎，喇培清，师婷，等.块体纳米晶／微米晶复相金属材料研究现状及其发展趋势［J］.材料工程，2013，（4）：92－96.WANG Hong－ding，LA Pei－qing，SHI Ting，et al.Research status and development trend of bulk nano／micro－crystalline composite metallic materials［J］.Journal of Materials Engineering，2013，（4）：92－96.

［3］ZHOU Yuan－xin，WANG Yang，MALLICK P K，et al.Strain softening constitutive equation for tungsten heavy alloy under tensile impact［J］.Materials Letters，2004，58（22－23）：2725－2729.

［4］刘海燕，宋卫东，宁建国.不同晶粒度钨合金动态力学性能研究［J］.材料工程，2007，（6）：3－6.LIU Hai－yan，SONG Wei－dong，NING Jian－guo.Dynamic behavior of tungsten alloys with different grain sizes［J］.Journal of Materials Engineering，2007，（6）：3－6.

［5］李娜，李玉龙，郭伟国.两种钨合金材料力学行为及微观损伤研究［J］.兵器材料科学与工程，2009，32（4）：99－103.LI Na，LI Yu－long，GUO Wei－guo.Study on the mechanical behaviors and microcosmic damage of two tungsten alloys［J］.Ordnance Material Science and Engineering，2009，32（4）：99－103.

［6］PINK E，KUMAR S.Deformation mechanisms operating in a tungsten heavy alloy［J］.Material Science and Engineering：A，1997，234－236（1）：102－105.

［7］KUMAR S，PINK E.Dynamic strain aging in a tungsten heavy metal［J］.Script Material，1996，35（9）：1047－1052.

［8］王世良，刘新利，张泉，等.钨合金微／纳米晶须：气相合成、生成机理、性能测试和应用前景［J］.中国钨业，2009，24（5）：86－92.WANG Shi－liang，LIU Xin－li，ZHANG Quan，et al.Single crystal tungsten micron－／nano－sized whiskers：vapor phase synthesis，growth mechanism，properties and application［J］.China Tungsten Industry，2009，24（5）：86－92.

［9］谷怀鹏，刘丽君，曹腊梅，等.含Ru镍基单晶高温合金的显微组织和拉伸性能研究［J］.航空材料学报，2013，（33）6：20－25.GU Huai－peng，LIU Li－jun，CAO La－mei，et al.Microstructure and tensile property of Ru－containing Ni base single crystal superalloy［J］.Journal of Aeronautical Materials，2013，（33）6：20－25.

［10］王建伟，尚新春，吕国才.bcc－Fe空位浓度对辐照损伤影响的分子动力学模拟［J］.材料工程，2011，（10）：15－18.WANG Jian－wei，SHANG Xin－chun，LU Guo－cai.Molecular dynamics simulation of vacancy concentration on cascades damage effects in bcc－Fe［J］.Journal of Materials Engineering，2011，（10）：15－18.

［11］汪文川，周健，曹达鹏，等.分子模拟－从算法到应用［M］.北京：化学工业出版社，2002.

［12］DAW M S，BASKES M I.Embedded－atom method：Derivation and application to impurities，surfaces and other defects in metals［J］.Physical Review B，1984，29（12）：6443－6453.

［13］陶杰，姚正军，薛烽.材料科学基础［M］.北京：化学工业出版社，2006.

［14］ACKLAND G J.Theoretical study of titanium surfaces and defects with a new many－body potential［J］.Phil Mag A，1992，66（6）：917－932.

［15］МИХАЙЛОВСКИЙИ М，ПОЛТИНИНПЯ，ФЕДОРОВА Л И.Авдоионно－микроскопи－ческое определение идеальной прочностиигольчатыхмикрокристалловволь－фрама［J］.Физика ТвердогоТела，1981，23（5）：1291－1295.

［16］STUKOWSKI A.Visualization and analysis of atomistic simulation data with ovito－the open visualization tool［J］.Modelling and Simulation in Materials Science and Engineering，2010，18（1）：1－6.