铝合金矩形管绕弯件尺寸精度的试验研究

杨 银，闫晓东，王 哲，陈 松，李 慧

(1.北京有色金属研究总院加工事业部，北京 100088;2.北京当升材料科技股份有限公司，北京 100070)

铝合金矩形管弯曲件由于具有质量轻、内部残余应力小、减震效果及稳定性好等特点，在航空、航天等领域有广泛应用［1－3］.矩形管的弯曲成形方法有很多，而绕弯成形由于其精度高、效率高且易实现自动化等优点，得到越来越多的应用.矩形管由于其形状的特殊性，在绕弯成形中除了会产生破裂、回弹、起皱等一系列普遍弯曲存在的缺陷外，还存在变形更加复杂的截面畸变［4－5］.目前管材弯曲的研究主要集中于各种弯曲方式产生的变形、缺陷分析及相对应的数值模拟，而矩形管绕弯成形的研究主要集中在数值模拟分析上，实验研究相对较少.赵刚要等［6］对矩形管绕弯成形失稳起皱进行了研究，模拟分析了工艺参数对薄壁矩形管绕弯成形失稳起皱的影响规律，为实验研究提供了理论基础.刘郁丽等［7－11］采用有限元数值模拟与试验相结合的方法，对H96薄壁矩形管绕弯和回弹过程管材的应力应变分布及变化规律进行了研究，同时分析了间隙对矩形管绕弯成形过程中截面畸变的影响，得出抽芯和回弹后，管材的应力明显减小，而应变几乎不发生改变，而减小芯棒与管坯间的间隙及弯曲模与管坯间的间隙都可以减小管坯截面畸变的程度，其他间隙对管坯截面畸变影响不大.

铝合金矩形管绕弯成形时，截面畸变及回弹等问题严重影响其零件的几何精度，而截面畸变及回弹受材料特性与工艺参数的双重影响，其中材料的力学性能与相对弯曲半径是两个主要的影响因素.因此本文通过实验对铝合金矩形管绕弯成形进行了研究，分析了材料的力学性能及相对弯曲半径对矩形管截面畸变与回弹的影响.

1 实验

1.1 材料

实验所用材料为冷加工态的6A02铝合金矩形管材，截面尺寸13 mm×12 mm，壁厚2 mm，其化学成分如表1所示.

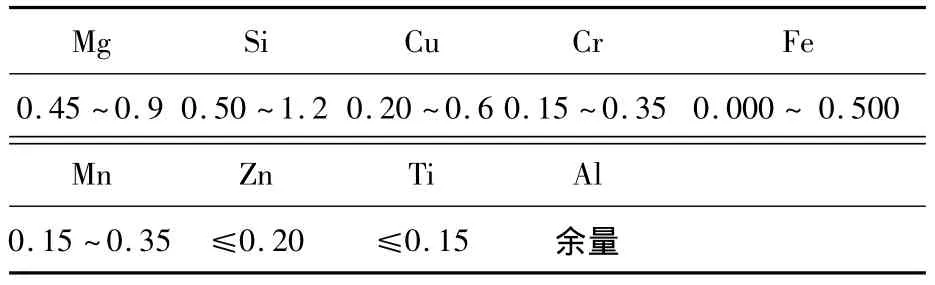
表16 A02铝合金的化学成分(质量分数/%)

将冷加工态的6A02铝合金矩形管材置于箱式电阻炉中，按不同工艺进行退火处理，冷却方式均采用炉冷至250℃再空冷.在不同退火工艺下的矩形管上截取一小段，制作力学性能测试标准样，在万能材料试验机进行力学性能测试，其力学性能结果如表2所示.其中:R0.2为材料屈服强度;Rm为材料抗拉强度;A为材料的延伸率;E为弹性模量.

表2 不同热处理制度下6A02铝合金的力学性能

1.2 实验方法

对不同力学性能的铝合金矩形管腔进行填充处理，填充物质为直径0.1 mm的小细沙.以沙子完全压实为准，对型材腔体两端进行封口，之后在弯曲模半径分别为92.4、101.8、119.6 mm 的绕弯装置上进行零件绕弯，绕弯装置图如图1所示.绕弯装置主要由弯曲模、侧压轮、夹头及导向板组成，通过夹头将矩形管材固定在弯曲模上，再将其压入侧压轮凹槽，弯曲模旋转时，带动矩形管转动，从而达到绕弯的目的.其中侧压力(P)为150～160 N/mm2，后张力(F)为25 ～26 MPa.弯曲后的实际样件如图2所示.

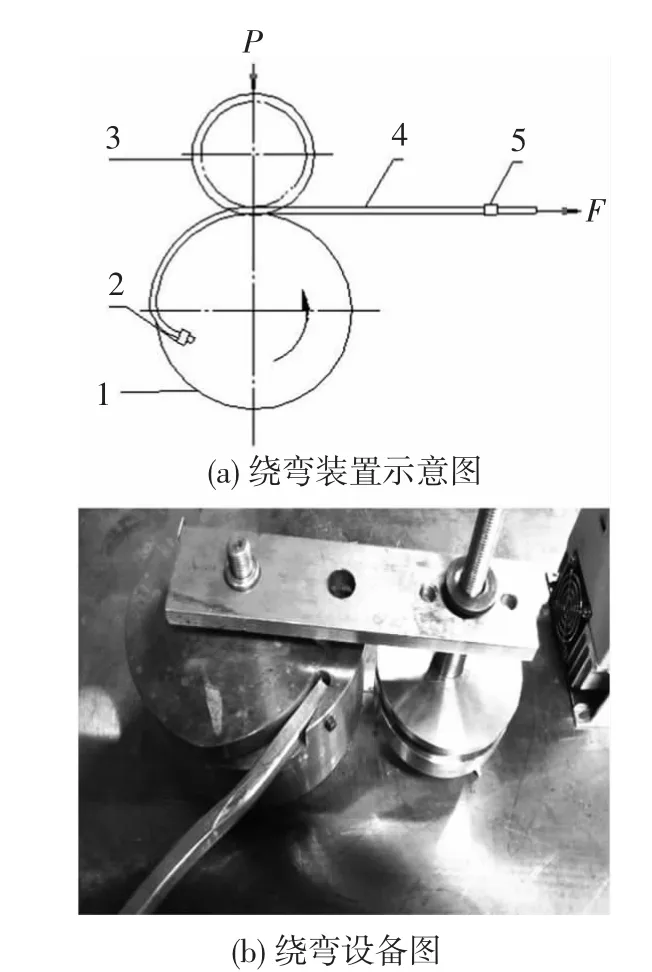
图1 绕弯装置图

图2 弯曲后实际样件图

2 截面畸变及回弹定义

截面畸变是影响管材绕弯成形精度的最主要因素之一.管坯在弯矩作用下弯曲时，管壁外侧受到切向拉应力，而内侧受到切向压应力，使得管壁材料在径向H方向产生压缩变形，且内外弯曲面容易产生塌陷，其变形前后示意图如图3所示.

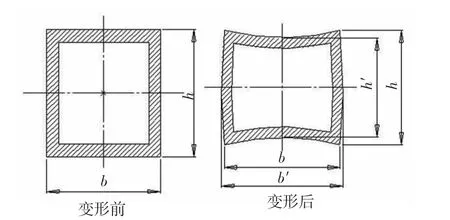
图3 绕弯前后矩形截面变形示意图

为了便于定量研究管材绕弯成形过程中的截面畸变，分别用δh和δb表示管坯沿径向和垂直径向方向的截面变化率，其表达如式(1)和式(2)所示:

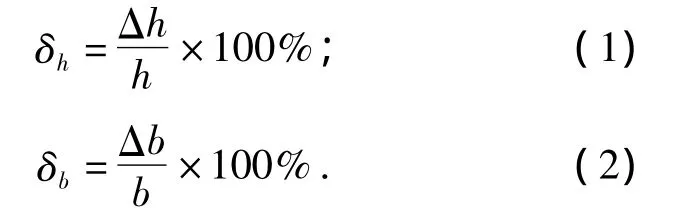
式中:Δh=h－h';Δb=b'－b;h和b分别为未变形管坯截面的高和宽;h'和b'分别为变形后管坯截面最小高度和最大宽度.由于后续处理的需要，合格的弯曲方管径向方向最大截面畸变率不能超过3.5%，垂直径向方向最大截面畸变率不能超过1%.

管材的绕弯成形是一个塑性变形与弹性变形相结合的过程［12］，卸载后，管材的塑性变形会保留下来，而弹性变形则完全消失，发生回弹，使得实际零件与模具形状不符，产生几何误差.绕弯件卸载前其曲率半径与绕弯模的曲率半径一样为R，卸载后由于弹复变形其曲率半径变为R'(绕弯件曲率半径平均值)，曲率半径的变化量△R称为曲率半径的回弹量，用δR表示曲率半径回弹率，其表达式为

式中，△R=R'－R.

为了研究弯曲后管坯沿圆周方向的截面畸变及回弹情况，定义离绕弯件一端离夹头一定距离的点为基准点.在基准点处中心角θ=0°，测量范围为0°～360°，按照弯曲方向每隔45°取一个截面，作为曲率半径的测量点，共9个截面，每一个截面径向方向与垂直径向方向各取5个节点，分别测量这几个节点的截面尺寸，选取各管坯截面最小高度和最大宽度，从而计算截面畸变率.由于周向各点的曲率半径是不一致的［13］，分别测量9个曲率半径测量点，取平均值，所测位置如图4所示.

图4 所测位置示意图

3 结果与讨论

3.1 屈服强度对矩形管截面畸变及回弹的影响

采用三坐标测量仪分别对屈服强度为62、70及91 MPa的管材绕弯前后的截面尺寸进行了测量，其截面畸变结果如图5和图6所示，弯曲时采用半径为101.8 mm的弯曲模，其他工艺参数均一致，具体参考试验方法.

图5 屈服强度对沿弯曲方向δh的影响

图6 屈服强度对沿弯曲方向δb的影响

图5为屈服强度对管材沿弯曲方向径向截面变化率的影响，可以看出，屈服强度越大，δh越大，且随着弯曲角度的增加，δh也逐渐增加，其原因为屈服强度小，材料容易屈服，则所需弯矩相对较小，弯曲过程中塑性变形能小，从而截面变形小［14］.随着弯曲角度的增加，管材所受等效应力也会逐渐增加［11］，根据线性强化模型

可知σe与εe呈线性关系，因此随着弯曲角度的增加，管材截面等效应变也会逐渐增加.δh反映的是管材径向方向截面畸变情况，因此σe也与δh呈线性关系，从而可推知随着弯曲角度的增加，δh也逐渐增加.

图6为屈服强度对管材沿弯曲方向垂直径向方向的截面变化率的影响，由图6可知，屈服强度越大，δb越大，与 δh变化规律类似，其区别为δb变化较小.且随着弯曲角度的增加，δb并没有相应的增加，而是上下起伏，说明弯曲角度的大小对δb的影响不大.根据最小阻力原理，管材径向方向外侧受到拉应力，内侧受到压应力，会向阻力较小的垂直径向方向流动，由于侧压轮凹槽宽度的限制，垂直径向方向的截面变化率较均匀.

由于后续处理的需要，对弯曲管材的最大截面畸变有严格的要求，大于文章所要求值即为不合格.综合不同屈服强度的绕弯成形截面畸变情况，发现屈服强度为91 MPa的管材绕弯后最大截面畸变率 δh达到 3.6%，δb达到 1.4%，已超出合格样件所要求值，弯管件不合格，而屈服强度在91 MPa以下的管材最大截面畸变率均低于合格样件所要求值，弯管件合格.

曲率半径的回弹率与材料的屈服强度息息相关，当材料的弹性模量，弯曲曲率半径一样时，理论上屈服强度越高，曲率半径的回弹率越大.对屈服强度为62、70及91 MPa的管材绕弯后卸载前与卸载后的曲率半径进行了测量，其回弹率结果如图7所示.

图7 屈服强度与曲率半径回弹率的关系曲线

由图7可知:屈服强度62 MPa的管材绕弯卸载后，曲率半径回弹率相对较小，大约在模具尺寸的基础上回弹16.75%;随着屈服强度的增加，绕弯卸载后圆环曲率半径回弹率也增加;屈服强度为70 MPa时，曲率半径回弹率约17%;屈服强度增加到91 MPa时，曲率半径回弹率达到17.6%，即弯曲曲率半径一致时，屈服强度越大，其曲率半径回弹量也越大，这样对制件的最终尺寸影响也越大.因此，在设计绕弯模具弯曲模尺寸时，应考虑屈服强度对曲率半径回弹率大小的影响.屈服强度为62 MPa时，弯曲模半径尺寸应设计为制件理论要求值的0.857;屈服强度为70 MPa时，弯曲模半径尺寸应设计为制件理论要求值的0.855;屈服强度为91 MPa时，弯曲模半径尺寸应设计为制件理论要求值的0.85.以此类推，当材料的屈服强度越大时，弯曲模半径尺寸设计值与制件理论要求值的比值越小，这样能有效控制回弹率对制件曲率半径的影响.此外，弯曲高强度材料时，可采取去应力退火的方式，降低材料的屈服强度，控制回弹率.

3.2 相对弯曲半径对矩形管截面畸变及回弹的影响

相对弯曲半径为绕弯模半径与矩形管坯截面高的比值，用R/H表示.图8、图9分别为屈服强度为70 MPa，相对弯曲半径为7.11、7.83、9.20时，绕弯后矩形管材径向与垂直径向方向的截面畸变结果图，其他工艺参数均一致.

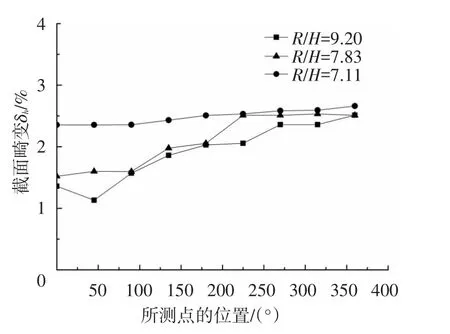
图8 相对弯曲半径对沿弯曲方向δh的影响

图9 相对弯曲半径对沿弯曲方向δb的影响

由图8可以看出:相对弯曲半径为7.11时，δh相对较大，接近2.5%;随着相对弯曲半径增加，其δh逐渐减小;当相对弯曲半径为9.2时，δh在2%以下;相对弯曲半径为7.83的δh处于二者之间，其原因为当弯曲角度一样时，相对弯曲半径越大，管材变形程度越小，矩形管材在高度上的截面变化率也小.由图9可以看出，相对弯曲半径为7.11、7.83、9.20 时，δb都较小且相差不大，均在0.25% ～0.75%，说明相对弯曲半径对 δb影响不大.另外，从实验结果可以看出，相对弯曲半径在7.11～9.20内，管材的截面畸变均未超出所要求值，弯管件合格.

图10为管材屈服强度为70 MPa时，相对弯曲半径对管材绕弯卸载后曲率半径回弹率影响的结果图.由图10可以看出:相对弯曲半径为7.11时，管材绕弯卸载后曲率半径回弹率相对较大，大约在模具尺寸的基础上回弹18.4%;随着相对弯曲半径的增加，曲率半径的回弹率反而减少，相对弯曲半径为7.83时，曲率半径回弹率约为17.4%，相对弯曲半径为9.20时，曲率半径回弹率减少到16.6%.一般相对弯曲半径越大，管材的弯曲变形程度越小，塑性变形区中的弹性变形所占的比例同时也增大［16］，曲率半径的回弹量也增加，而曲率半径的回弹率相当于回弹量与曲率半径的比值，与单位长度的回弹量的变化保持一致.相对弯曲半径越小，单位长度相对弯曲角越大，其回弹量就越大，从而曲率半径回弹率也会越大［17］.

图10 相对弯曲半径与曲率半径回弹率的关系图

4 结论

1)随着屈服强度的增加大，δh、δb也增加，但δb变化相对较小，且随着弯曲角度的增加，δh逐渐增加，δb并没有相应的增加，而是上下起伏，说明弯曲角度的大小对δb的影响不大.

2)随着屈服强度的增加，绕弯卸载后曲率半径的回弹率也增加.屈服强度为62 MPa时，大约在模具尺寸的基础上回弹16.75%;屈服强度为70 MPa时，曲率半径回弹率约为17%;当屈服强度增加到91 MPa时，曲率半径回弹率相应增加到17.6%.当材料的屈服强度越大时，弯曲模半径尺寸设计值与制件理论要求值的比值越小，可有效控制回弹率对制件曲率半径的影响.

3)随着相对弯曲半径的增加，δh逐渐减小，δb相差甚微，均在0.25% ～0.75%，曲率半径的回弹率也相应减少.相对弯曲半径为7.11时，δh相对较大，接近2.5%，曲率半径回弹率相对较大，大约在模具尺寸的基础上回弹18.4%.相对弯曲半径为7.83的δh处于2% ～2.5%之间，曲率半径回弹率约为17.4%;当相对弯曲半径为9.2时，δh在2%以下，曲率半径回弹率减少到16.6%.

［1］ 刘郁丽，杨合，张津.铝合金薄壁矩形管绕弯成形壁厚分布规律研究［J］.材料科学与工艺，2010，18(增刊1):1－4.LIU Yuli，YANG He，ZHANG Jin. Research on distribution laws of wall thickness of aluminum alloy thin-walled rectangular tube in rotary draw bending process［J］.Material Science ＆ Technology，2010，10(sup 1):1－4.

［2］ LI H，YANG H，ZHAN M，et al.Deformation behaviors of thin-walled tube in rotary draw bending under push assistant loading conditions［J］.Journal of Materials Processing Technology，2010，210(1):143 －158.

［3］ SHEN Huawen，LIU Yuli，QI Haiyan，et al.Relations between the stress components and cross-sectional distortion of thin-wallled rectangular waveguide tube in rotary draw bending process［J］.Int J Adv Manuf Technol，2013，68:651 －662.

［4］ 温彤，丰慧珍，艾百胜.管材绕弯变形的理论与实验分析［J］.重庆大学学报，2006，29(12):8－12.WEN Tong，FENG Huizhen，AI Baisheng.Theoretical and experimental study on the deformation of pipe rotary-draw bending ［J］. JournalofChongqing University，2006，29(12):8 －12.

［5］ UTSUMI N，SAKAKI S.Countermeasures against undesirable phenomena in the draw-bending process for extruded square tubes［J］.Journal of Materials Processing Technology，2002，123(2):264－269.

［6］ 赵刚要.薄壁矩形管绕弯成形失稳起皱的数值模拟［D］.西安:西北工业大学，2007:71.

［7］ ZHAO Gangyao，LIU Yuli，YANG He.Effect of clearance on wrinkling of thin-walled rectangular tube in rotary draw bending process［J］.Int J Adv Manuf Technol，2010，50:85 －92.

［8］ 刘郁丽，任家海，朱英霞，等.H96薄壁矩形管绕弯回弹过程的应力应变分析［J］.锻压技术，2012，37(1):146－148.LIU Yuli，REN Jiahai，ZHU Yingxia，et al. Stress strain analysis of the thin walled rectangular tube of H96 brass in the process of bending and spring-back［J］.Forging＆ Stamping Technology，2012，37(1):146－148.

［9］ 沈化文，刘郁丽，董文倩，等.芯棒对铝合金矩形管绕弯回弹作用的数值模拟［J］.材料科学与工艺，2012，20(1):38－43.SHEN Huawen，LIU Yuli，DONG Wenqian，et al.Numerical simulation of effects of mandrel on springback of aluminum alloy rectangular tube in rotary-draw bending process［J］. Materials Science and Technology，2012，20(1):38－43.

［10］ ZHAO G Y，ZHANG R Y，LIU Y L，et al.A new method to accurately describe cross-section distortion in rotary draw bending process of thin-walled rectangulartube［J］. Applied Mechanics and Materials，2012，117－119:1839－1842.

［11］ 刘郁丽，卢彩虹，赵刚要，等.间隙对薄壁矩形管绕弯成形截面畸变影响的研究［J］.中国机械工程，2008，19(16):1972－1975.LIU Yuli，LU Caihong，ZHAO Gangyao，et al.Effect of clearance on cross section distortion of thin-walled rectangular tube in rotary draw bending process［J］.Chinese Mechanical Engineering，2008，19(16):1972－1975.

［12］ AL-QURESHI H A.Elastic-plastic analysis of tube bending［J］.International Journal of Machine Tools and Manufacture，1999，39(1):87－104.

［13］ 杨玉英，董昀，赵立红.帽形型材绕弯件的曲率一致性［J］.材料科学与工艺，2004，12(1):91－94.YANGYuying，DONGYun，ZHAOLihong. The curvature consistency of hat-section profiles in rotary draw bending［J］.Materials Science ＆ Technology，2004，12(1):91－94.

［14］ 张津，刘郁丽，赵刚要，等.材料参数对矩形管绕弯截面变形的影响［J］.热加工工艺，2009，38(13):1－4.ZHANG Jin，LIU Yuli，ZHAO Gangyao，et al.Influence of material parameters on rectangular tube crosssection deformation in rotary-draw bending process［J］.Hot Working Technology，2009，38(13):1－4.

［15］ 彭大暑.金属塑性加工原理［M］.长沙:中南大学出版社，2006:46

［16］ 成虹.冲压工艺与模具设计［M］.北京:高等教育出版社，2001:112

［17］ 韩盛夏.基于回弹的液压成形模快速设计技术研究［D］.沈阳:沈阳航空工业学院，2010:6