数值保角变换的新算法

姚国梅YAO Guo-mei；吕毅斌LV Yi-bin；王樱子WANG Ying-zi

（①昆明理工大学理学院，昆明 650500；②昆明理工大学计算中心，昆明 650500）

（①Faculty of Science，Kunming University of Science and Technology，Kunming 650500，China；②Computing Center，Kunming University of Science and Technology，Kunming 650500，China）

0 引言

数值保角变换是复变函数的一个基本问题，它广泛应用于物理学和工学等领域。在大多数情况下，需要通过数值计算求解满足被给定条件的变化函数。保角变换的变换函数求解方法一般可以分为解析法和数值方法。对于解析法，只有在极少数的情况下能用初等函数表示保角变换函数，因此很多情况下，仅仅指出了变换函数的存在，而不能求出变换函数。基于实际工程问题的复杂性，在大多数情况下必须利用数值方法求解满足被给定条件下的保角变换问题。很多学者对此做了大量研究[5-9]。

本论文研究在模拟电荷法下基于改进高斯消去法的数值计算法来求解保角变换问题，文中首先用模拟电荷法原理通过电荷点和约束点构造约束方程，再利用改进高斯消去法的高精度求解该约束方程，得到模拟电荷和近似保角变换半径，进而构造出近似保角变换函数，并在文章结尾通过数值实验验证算法的有效性。

1 模拟电荷点的计算

本节主要讲述利用模拟电荷法对区域外部计算保角变换的数值方法（如图1）[11]。在图1 中，C 是z 平面上任意的Jordan 曲线，曲线C 的区域外部作为D，ζj（j=1，2，…，N）是在区域内部配置的电荷点，zi（i=1，2，…，N）是边界C上的约束点，w=f（z）是从（这里=D∪C）到w 平面上的单位圆外部（包括单位圆边界）的保角映射。在不失一般性的情况下，假定z=0 在C 的内部且f（0）=0，保角变换函数w=f（z）满足正规化条件f（∞）=∞，f′（∞）＞0 时表示如下：

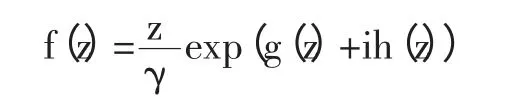
其中，γ 是外部变换半径，g（z）是Dirichlet 型场势问题：

的解。h（z）是g（z）的共轭调和函数，且h（∞）=0。以下文中均以G，H，Γ 表示g，h，γ 的近似值。

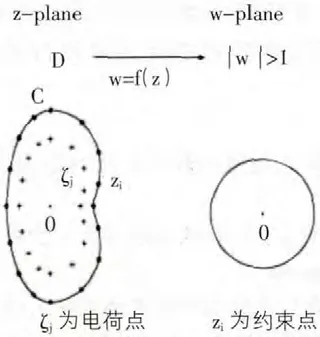
图1 基于模拟电荷法的数值保角变换

根据模拟电荷法（图1），可以用围绕C 的区域内部配置的电荷点ζj（j=1，2，…，N）作为极的对数势场的1 维结合

来高度近似g（z）[11]，这时g（z）的共轭调和函数h（z）可以被如下函数近似：

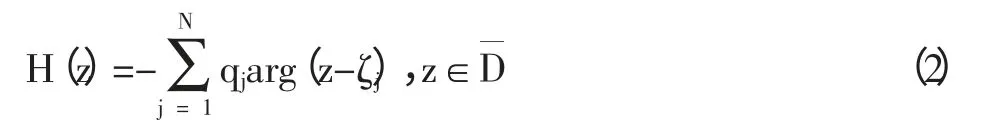
未知电荷qj可以通过边界上选择N 个约束点zi在满足外部Dirichlet 问题的边界条件进行求解，即满足：

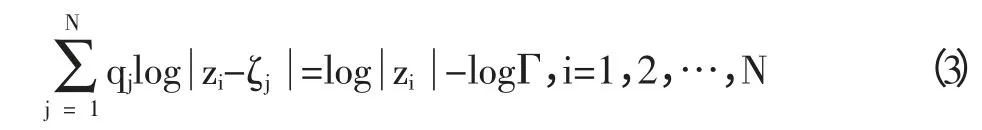
又根据条件g（∞）=0，h（∞）=0，由式（1），（2）可得：

由式（3）和（4）可知qj（j=1，2，…，N）和logΓ 满足下列线性方程组：

2 数值保角变换的新算法

通过上节讨论，根据模拟电荷法的原理，在求解模拟电荷点以及近似变换半径过程中，首先，要用围绕C 的区域内部配置N 个电荷点作为极的对数势场的1 次结合的G（z）来高度近似g（z），而它的共轭调和函数h（z）则用H（z）来近似，再通过边界条件以及电荷点和约束点的配置构造出约束方程（5）。因此，数值保角变换的算法过程整理如下。

数值保角变换的算法：①给出模拟电荷法的模拟电荷和约束点数量N；②根据模拟电荷法的原理[11]，给出电荷点ζ1，…，ζN，约束点z1，…，zN；③由模拟电荷点和约束点以及变换半径构造约束方程组（5）；④计算模拟电荷q1，…，qN和变换半径Γ；⑤根据（1）式和（2）式构造G（z），H（z）；⑥构造近似保角变换函数。

在上述算法过程中，第4 步模拟电荷q1，…，qN和变换半径Γ 的计算结果对保角变换的精度影响很大。因此，为了高精度地求解模拟电荷和近似变换半径，采用辗转相除法的高斯消去法[1-4]求解约束方程（5），进而得到高精度的模拟电荷和变换半径。

本文的做法是：

①整数处理：如果方程组的系数不是整数，则在方程两边同时乘以10w（w 为正整数）使其变为整数（参见表1）；②非负处理：若所要消元的系数为负，则通过同乘-1使其变为正数（参见表2）；③换行：若所要消元的系数不是非零最小，则交换方程位置变为最小（参见表3）；④整数倍消元：若所要消元系数相除时不能整除，则对系数相除取整（参见表4）。这样做可以使原方程组化为等价方程的过程中不出现除法，从而可以绝对消除因除法带来的累积误差。（下列表中，[ ]表示取整符号，&表示逻辑语句且，↔表示换行，←表示赋值。）

表1 整数处理

表2 非负处理

表3 换行

表4 整数倍消元

3 数值实验

在模拟电荷法下基于改进高斯消去法的方法对椭圆外部的保角变换进行数值实验。程序用MATLAB7.0 编写，误差结果采用倍精度计算。误差的定义是由边界C 上的点所对应的保角变换点与边界保角变换所得单位圆盘圆周半径方向的最大距离。[10]误差计算公式如下：

电荷点和约束点的配置问题参考文献[11]。

①当a=3 时，数值实验结果参见图2 和图3。

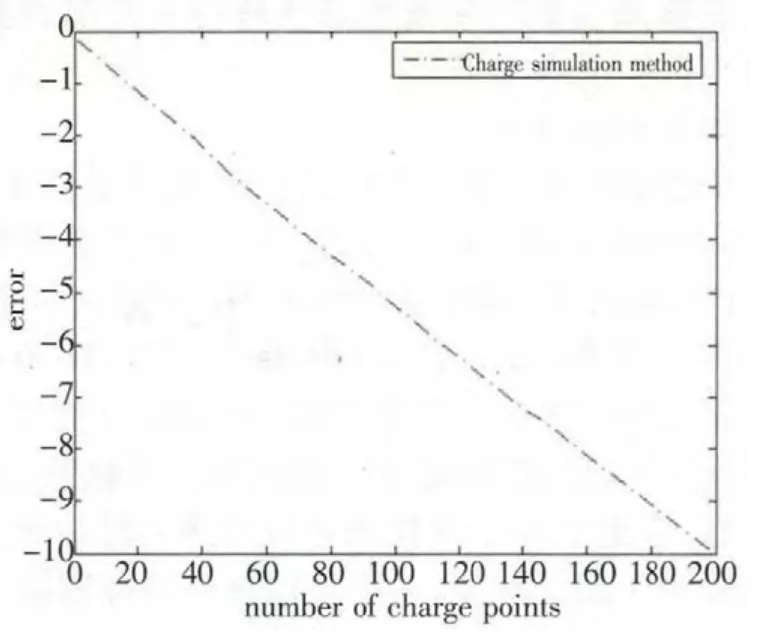
图3 a=3

图2 给出了N=200 时模拟电荷的分布位置（“+”表示模拟电荷位置）；而图3 则给出了在a=3 时近似保角变换的误差结果图，在图3 中横坐标表示电荷点的个数，纵坐标则表示误差。由图3 可以看出随着电荷点数的增加，误差结果将会变小。

②当a=5 时，数值实验结果参见图4 和图5。

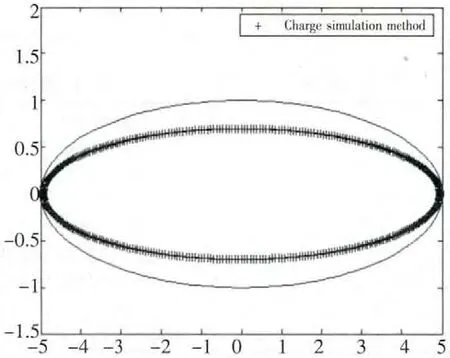
图4 a=5，N=200

类似的，图4 给出了N=200 时模拟电荷的分布位置（“+”表示模拟电荷位置）；图5 则给出了在a=5 时近似保角变换的误差结果图，由图5 可以看出随着模拟电荷数的增加，误差结果越来越小。

上述实验说明，随着模拟电荷点数的取值越多，本算法保角变换的计算精度越高。因此根据计算精度要求，可以提前确定所需模拟电荷点的数量。

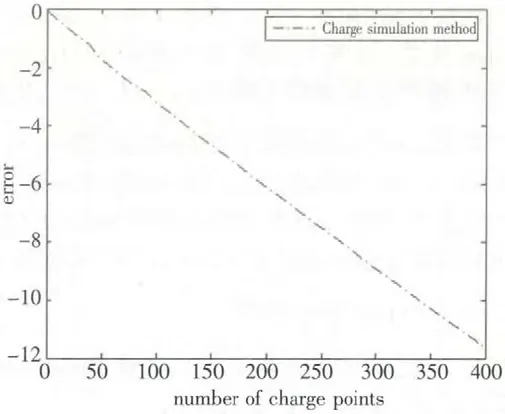
图5 a=5

4 结论

本文在模拟电荷法的原理下，利用改进高斯消去法高精度地计算了模拟电荷点，进而提出了高精度的保角变换的新算法，然后通过典型图形的数值实验验证了该算法的有效性。今后对本算法进行误差分析，然后可以将其运用到多连通区域的数值保角变换以及流体力学中的涡流计算问题。

[1]聂学建.关于线性代数中的秩[J].职大学报，2013（04）：75-77.

[2]文传军，许定亮，华婷.高斯消元五步骤法[J].常州工学院学报，2012（06）：56-59.

[3]彭朝英.高斯消元法的改进及其在工程上的应用[J].邵阳学院学报：自然科学版，2011（02）：31-35.

[4]胡尧，罗文俊.改进Gauss 消去法求解线性方程组[J].贵州大学学报：自然科学版，2004（02）:19-23.

[5]Yunus A A M，Murid A H M，Nasser M M S.Numerical conformal mapping and its inverse of unbounded multiply connected regions onto logarithmic spiral slit regions and straight slit regions[J].Proceedings of the Royal Society A:Mathematical，Physical and Engineering Science，2014，470(2162):20130514.

[6]Lu Y，Wu D，Wang Y，et al.The accuracy improvement of numerical conformal mapping using the modified Gram-Schmidt method [C].The 19th International Conference on Industrial Engineering and Engineering Management.Springer Berlin Heidelberg，2013:555-563.

[7]Nasser M.Numerical conformal mapping of multiply connected regions onto the second，third and fourth categories of Koebe's canonical slit domains [J].Journal of Mathematical Analysis and Applications，2011，382(1):47-56.

[8]Luo W，Dai J，Gu X，et al.Numerical conformal mapping of multiply connected domains to regions with circular boundaries[J].Journal of Computational and Applied Mathematics，2010，233(11):2940-2947.

[9]Amano K，Okano D，Ogata H，et al.Numerical conformal mappings onto the linear slit domain [J].Japan Journal of Industrial and Applied Mathematics，2012，29(2):165-186.

[10]Amano K.Numerical conformal mapping of exterior domains based on the charge simulation method [J].Trans Inform Process Soc Japan，1988，29:62-72.(in Japanese).

[11]Amano K.Numerical conformal mapping based on the charge simulation method [J].Trans Inform Process Soc Japan，1987，28:697-704.(in Japanese).