大地电磁相位张量分解特性

陈江平CHEN Jiang-ping；周亚东ZHOU Ya-dong

（成都理工大学地球物理学院，成都 610059）

（College of Geophysics，Chengdu University of Technology，Chengdu 610059，China）

0 引言

Swift 分解是将大地电磁张量Z 在水平面内旋转，使之与区域构造主轴达到最佳匹配的方法。严格的说，Swift分解法适合用于标准的二维构造。对观测阻抗张量做该分解后，产生区域构造的两个主轴阻抗和构造的主轴方位角，即从观测阻抗张量四个复数元素（八个标量参数）进行旋转分析[1]。通常情况下，实际构造并不是标准的二维构造，故观测阻抗张量将含局部畸变的影响，分解结果并不是很精确。阻抗相位张量旋转可以消除观测阻抗张量电场局部畸变的影响，而且不需要关于区域结构维性的假设。对转换后的观测阻抗采用已有的Swift 旋转优化方法即可求得区域主轴方位角[2]。

1 阻抗相位张量分解原理

地表的测量坐标系xyz 中，非均匀介质的大地电磁阻抗张量为：Zxx，Zxy，Zyx，Zyy。

分离复杂的阻抗张量得到他们的实部（X）和虚部（Y），我们可以写为：

因此，我们定义阻抗相位张量的关系：

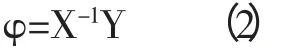
大地电磁的观测阻抗可以表示为：

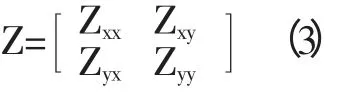
因此我们可以得到阻抗相位张量为：

只要把实际观测的阻抗张量（3）按照（2）式进行相位变换得到（4），在新的转换基础上，按照与经典的Swift 完全相似的办法，求得阻抗张量的一系列重要参数[3]。

2 确定主轴的最佳方位

对于转换的相位阻抗张量，根据Swift 旋转公式可获得平面上任意坐标系的转换阻抗。现使得旋转后目标函数：

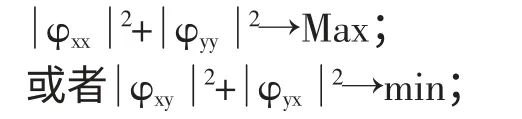
则可获得最佳主轴方位角为：

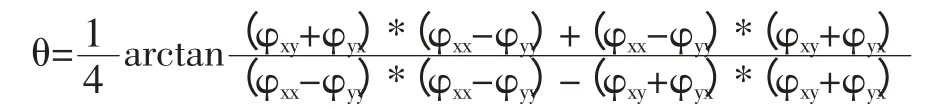
由上式可得到4 个解，按照与Swift 旋转相似的方式，通过比较目标函数值的大小来确定正确的结果。

3 理论模型分析

为说明阻抗相位张量方法不受电场局部畸变的影响，我们使用典型的二维模型的阻抗数据进行检验。

模型参数：走向沿正北方向的二维区域结构模型，

再把（5）中的二维模型加入电场畸变，畸变矩阵为：

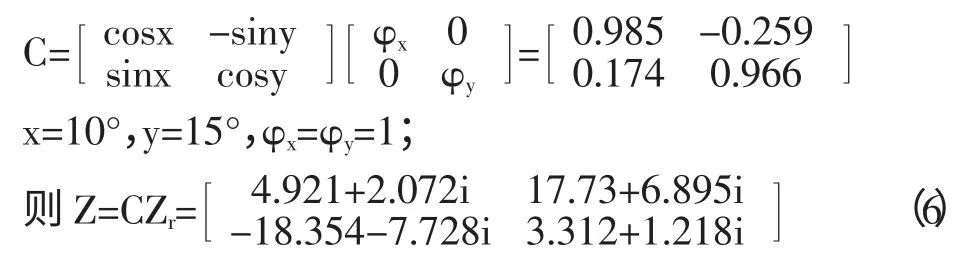
我们把加入电场畸变后的二维模型进行Swift 旋转、相位旋转和Bahr 旋转后。主轴方位角Swift 旋转有一定的偏差，偏差为2.34°；而Bahr 和相位都能很好地旋转到最佳主轴方位。

从中我们可以看出，当我们的二维模型受到电场畸变时，Swift 方法求得的主轴方位角有一定的偏差。而相位方法和Bahr 可以不受电场畸变的影响，但是相位方法有跟好的优化性。

4 实例

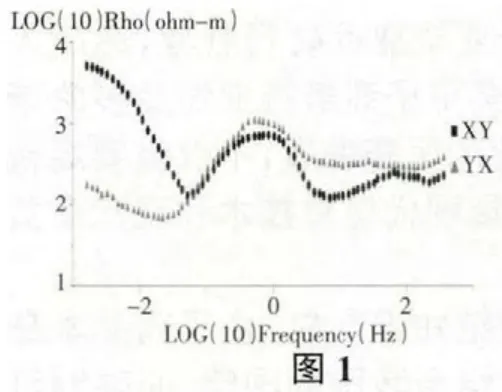
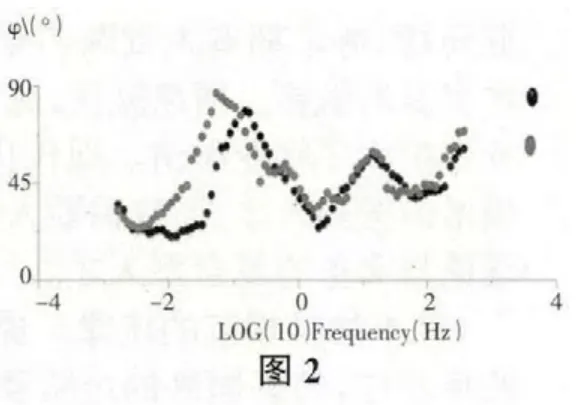
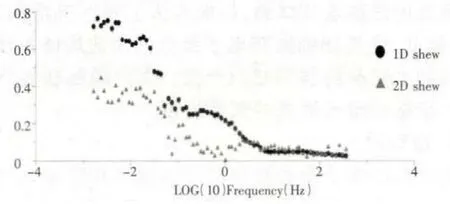
图3

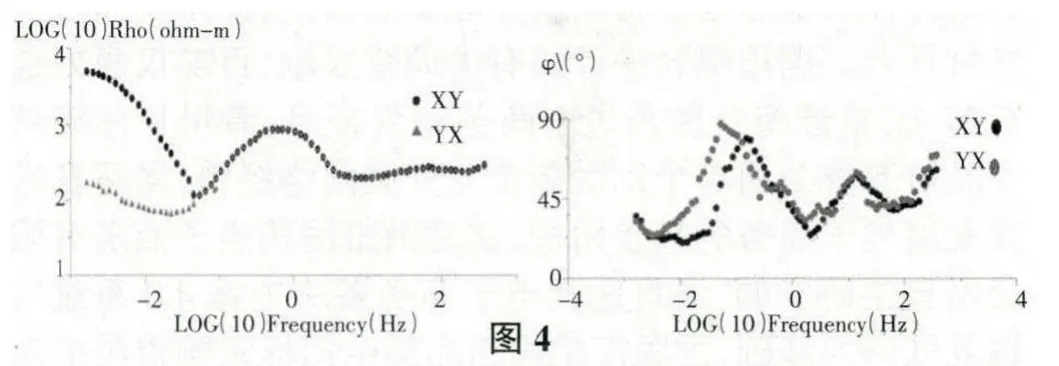
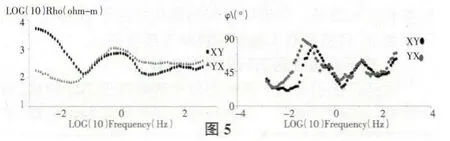
我们使用的数据实例是龙门山地区的某测点的数据，主要说明相位方法不受电场畸变的影响。如图1（XY 表示TE 模式、YX 表示TM 模式）、图2（相位曲线）我们可以看到TE 和TM 视电阻率曲线是分开的，表明可能受到浅部不均匀体的影响。图3 是实测数据的一维偏离度和二维偏离度，在频率10HZ 以上的部分，其一维偏离度和二维偏离度都很小，说明在该部分，其构造应该是一维的。在频率0.044HZ～10HZ 部分，其一维偏离度偏大，而二维偏离度较小，说明该部分结构是二维的。在频率小于0.44HZ 的部分，其一维偏离度和二维偏离度都比较大，说明这部分的构造大概是三维的。我们使用相位方法对实测数据进行了校正，而且将实测数据直接旋转到最佳主轴方位进行了对比。如图4（使用相位方法校正后的视电阻率曲线和相位），我们可以看出，在使用相位方法校正后，视电阻率的中高频部分已经重合，说明局部电场畸变的影响已经消除。而直接将实测数据旋转到最佳主轴方向，其视电阻率曲线仍然为分开的，说明局部畸变的影响仍然存在。同时在图4、图5（不做畸变处理直接旋转到主轴式电阻率和相位）中，我们可以看出畸变对相位信息是没有做任何改变的。

5 结论

对大地电磁观测阻抗进行相位变换后，可以消除电场局部畸变对观测阻抗张量的影响。我们对转换后的观测阻抗使用Swift 旋转优化方法即可求得区域主轴方位角。我们采用合成理论数据说明了相位方法对局部电场畸变影响的正确性，此外相位方法相对于Bahr 方法有跟好的稳定性、优化性。该方法只能进行单频点分析，多频点分解技术难以进行。因此我们下一步的工作将是推广到多点多频，并采用最优化技术分解。

[1]晋光文，孔祥儒.大地电磁阻抗张量的畸变与分解.北京：地震出版社，2006.

[2]蔡军涛，陈小斌，赵国泽.大地电磁资料精细处理和二维反演技术研究——阻抗张量分解与构造维性分析[J].地球物理学报，2010.

[3]T.Grant Caldwell,Hugh M.Bibby,Colin Brown.The magnetotelluric phase tensor.Geophysical Journal International,2004.