基于多体系统的龙门机床装配方案及预估优化

刘志峰，李端端，刘壮壮，安国平，赵永胜，郭宏升

（1.北京工业大学 机械工程与应用电子技术学院，北京 100124；2.北京北一机床股份有限公司，北京 101300）

0 引言

龙门机床的装配设计是其生产制造的重要环节，因为龙门机床的设计制造成本高、周期长，各个装配单元的差异较大，尺寸、装配方向、装配工具多变，而其质量、周期和精度等诸多因素都会在装配阶段反映出来，所以更需要在设计初期就对装配环节的情况进行预估和仿真分析，以最大限度地提高机床性能。总之，龙门机床的装配方案预估优化具有重要的理论和实用意义。

龙门机床装配涉及领域较多。国内方面，浙江大学魏喆［1］、天津大学邢德强［2］等利用性能驱动理论解决复杂机械产品（包括装配在内）的一些设计上的问题；北京航空航天大学王永等［3］提出一套将复杂产品分解为易于规划的独立模块的思路；浙江大学刘振宇［4］提出面向过程的虚拟装配建模方法；北京理工大学刘检华等［5］进行了手工装配与计算机辅助有机结合方面的研究；华中科技大学王峻峰［6］提出针对飞机制造领域的多自由度工装的运动构件结构和层次模型。国外方面，Hwai-En［7］提出一个较为细致的装配方案计算工具；Christiand［8］提出基于触觉式的装配优化方法；Deviprasad［9］对虚拟环境下的原型设计装配进程进行了详细的研究。此外，还有其他一些国内外学者都对装配的各方面有过研究，但相当数量的研究都局限于功能部件，针对整机装配方案分析及预估的方法较少。

本文基于多体理论，建立了一个反映龙门机床装配的计算方法，该方法能够直观、快速、分步地提供一套详细的可行方案，并判断不同方案的优劣，有效分析装配过程中某一单元的调整对其他单元造成的影响，从而使方案更为优化。所开发的软件工具能够求解出具体方案，实现各模块间的叠加分析，同时利用多指标面积图示直观反映优化效果。

1 基于多体理论的装配体建模

本章基于多体理论，以矩阵的形式描述装配单元及装配过程，通过对装配单元状态描述矩阵、装配过程描述矩阵的推导，建立龙门机床的装配体模型。

1.1 多体理论基础

根据龙门机床的结构与运动特点，将其抽象成多体系统［10］，用拓扑结构和低序体阵列描述机床各部分的关联性；在多体系统中建立广义坐标系，用矩阵描述机床各部件装配参数之间的耦合关系；推导出机床中两相邻体装配工作的特征矩阵和装配传递方程，从而建立龙门机床的装配模型。机床的结构简图如图1所示，它由滑轨、导轨、立柱、连接梁、横梁、溜板、主轴及铣头8部件组成。

根据多体系统理论的方法，将机床各组成部件分成相应的“体”，如图2所示。根据机床结构和各部件间的装配情况，建立各相邻体间的多体系统特征矩阵。表1所示为基于多体系统的龙门机床各部件间的特征矩阵。通过多体系统理论可以将机床各组成部件间的联系表现为矩阵连乘的形式，以便于进一步研究。

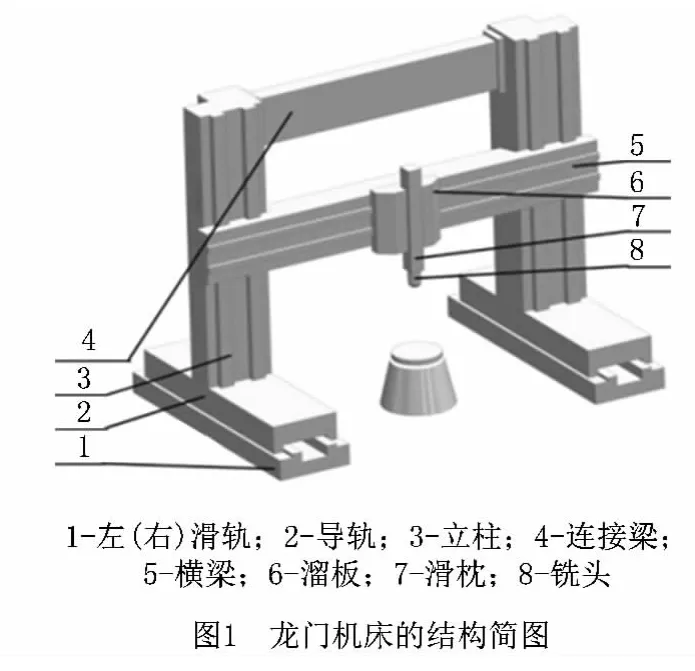
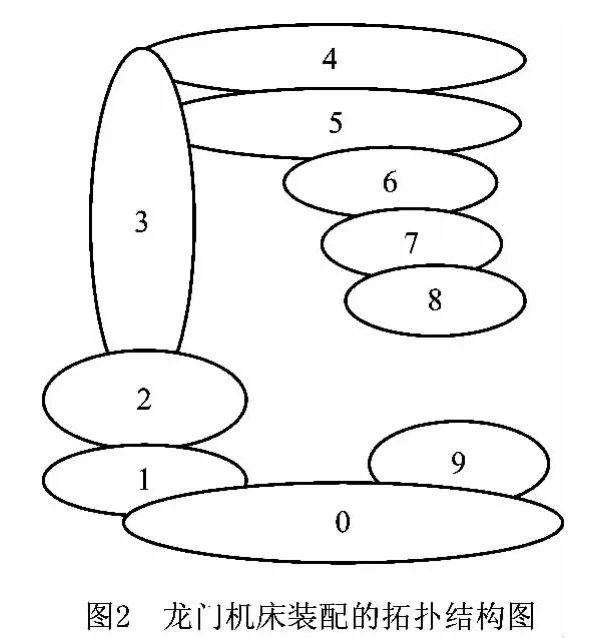
表1 龙门机床部件的特征矩阵（部分）

因为龙门机床的装配路线较为规范，无需对装配路线进行求解，所以不受装配干涉矩阵的影响，多体系统中各体间的装配关系可以用相应的矩阵及其运算变换来表示（如式（1）），系统每进行一个单元MU的装配，就乘一个MS作为表示。

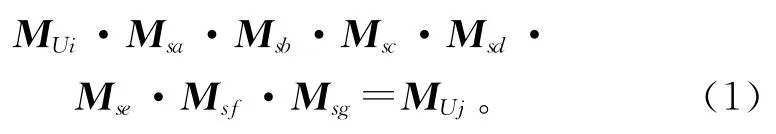
式中：MUi为装配单元状态描述矩阵；MUj为装配过程描述矩阵。

1.2 装配单元状态描述矩阵MU

考虑到龙门机床装配过程具有无需计算装配路线、各单元的装配方向多变、各件间的装配方式仅为栓接和滑接、装配单元间的诸多参数差异较大的固有特点，将装配状态的描述方式和参数进行取舍之后，对装配描述矩阵的所有可能性一一进行比较，得出装配描述矩阵边界条件内的最优解，建立无量纲的装配单元描述矩阵

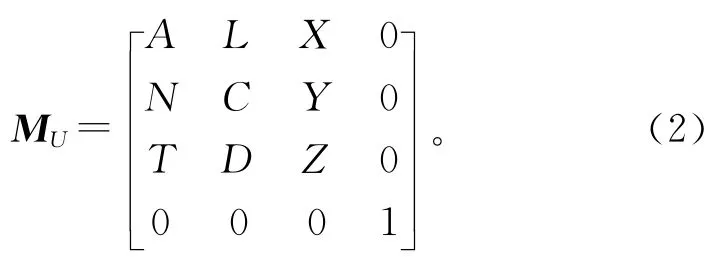
式中：A 为前一装配单元的装配方式［3］，滑轨连接为2，螺栓连接为1；L 为与前一装配单元的连接强度［3］，滑轨为0.2，螺栓为0.6；N 为装配参数，滑轨连接为轨道数，螺栓连接为螺栓个数；C 为约束自由度，是现有单元装配后系统的自由度；T 为配合精度，判断单元间是否有精度要求，有为1，没有为0；D 为装配方向相关性，与前单元装配方向一致为1，否则为-1；XYZ 为该单元装配后的偏移情况，理想值为1。

1.3 装配过程描述矩阵Ms

建立描述两装配单元间装配过程的矩阵Ms。引入装配中较为重要的三个参数Q（质量系数）、T（时间系数）和C（相关系数），作为XYZ 三轴向量的描述参数。单个装配单元装配过程的描述矩阵Ms通式表示为

式中：Q 为精度的调整情况，T 为装配周期的长度，C 为一个与精度Q 和装配周期T 相关的参数。

2 装配优化的求解

本章通过矩阵计算求得装配过程描述矩阵的理想值，并确定求解判据和优化判据的相关参数。

2.1 装配过程的描述矩阵Ms基准值

由实际装配关系将两装配单元及其装配过程描述为矩阵乘式

通过矩阵计算可知

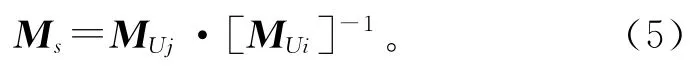
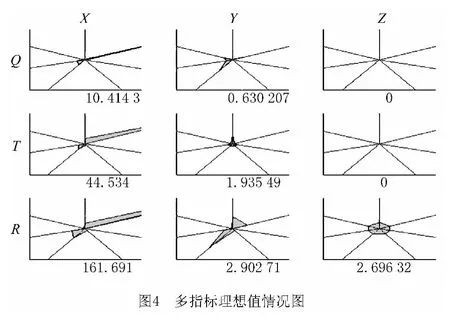
由式（5）计算即可求得理想的装配过程矩阵Ms。如果某单元Z 轴的精度调整ZQ 与耗费时间ZT 的值都是0，则说明理想状态下，该模块装配时只需调整XY 轴的变化而不必考虑Z 轴，显然与实际情况不符，因此在仿真分析时需赋予一个0.1～0.000 1范围的参数予以修正。

2.2 求解判据的主要参数

在求得的装配状态描述矩阵MUi中，自由度参数C 和MUj的XYZ 偏移值都满足条件才为可取解。龙门铣床的实际自由度为4，正常情况下，自由度的值应该随装配进程平稳增加，如图3所示。因此若自由度参数C 的绝对值与理想值超过1，则为非法解；若XYZ 偏移绝对值大于1，则说明此时装配的实际误差过大，不符合机床原本的设计要求，为不可取解。

2.3 优化判据的主要参数

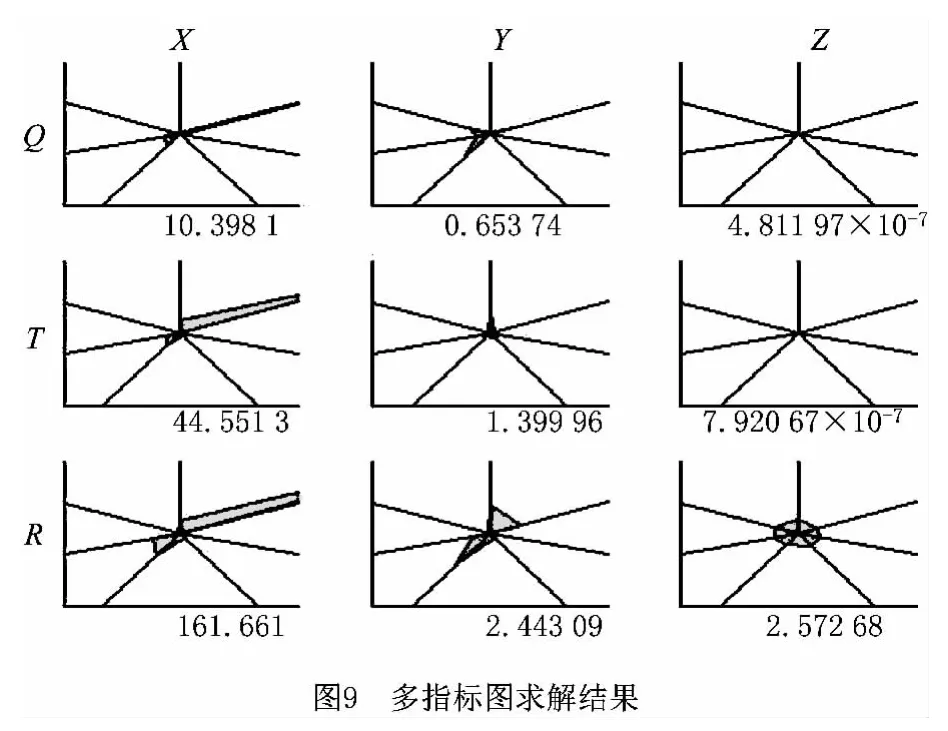
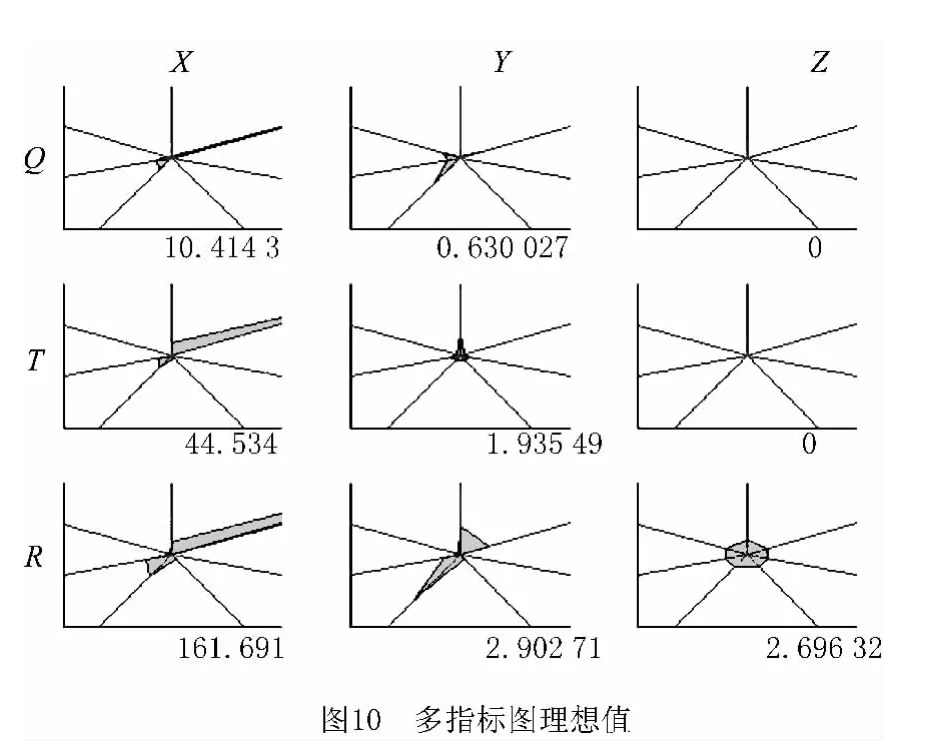
在可取解范围内，评估优化质量主要由“多指标示意图”的面积来决定。如图4所示，图中的极坐标轴自0°开始依次为从导轨到铣头的七个装配过程描述矩阵Ms，其坐标取值即装配过程描述矩阵中参数的值，每单个小图下方所标的数字即该图中以矩阵参数为顶点的多边形面积，此时为理想状态下的值，是比对多指标综合后的依据，面积越小，优化的效果越好。

2.4 优化判据的次要参数

在可取解范围内，任何装配单元单个参数的数值都可以进行微调。引入如图5所示的柱状图，柱状图每一个小图对应Ms矩阵同位置的参数，小图中由左至右为Ms1到Ms7的参数。将优化前与优化后的柱状图进行对比，可直观、有效地反映优化求解的正确性。

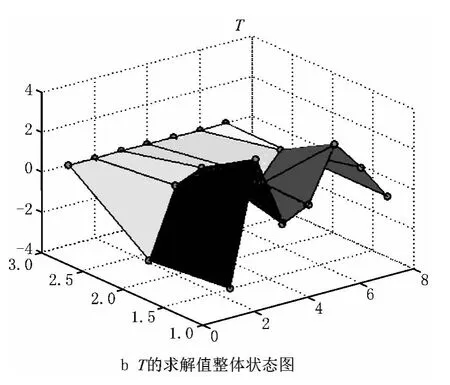
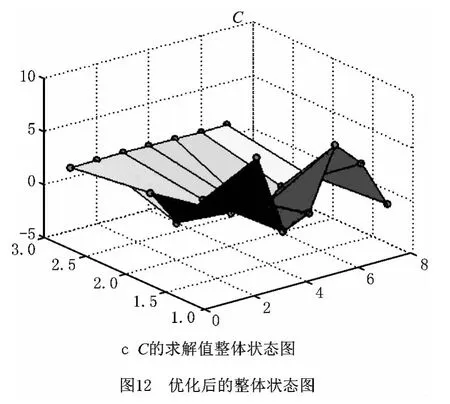
此外，单独将质量系数Q 的XYZ 轴数据提取出来，绘制只反映Q 的参数变化的三维图像，称为Q 的整体状态图，如图6a所示。该图作为优化求解的另一个直观参考，如果图中没有显示超出数据范围，则说明优化调整的参数处于合理的范围。同理，可绘制时间系数T 和相关系数C 的整体状态图，如图6b和图6c所示。

3 仿真实例

根据龙门机床各装配单元设计参数获得装配单元状态描述矩阵，并求解出装配过程描述矩阵。基于MATLAB开发专用计算软件求解基准值，通过对参数的调整分析可取解的范围，并对求解结果进行评估。

3.1 Ms和MU的求解

由龙门机床的设计参数，可得各单元状态描述矩阵MU。例如，龙门机床的床身为螺栓连接，数目为96个，自由度为0，有配合精度，不改变装配方向，其状态描述矩阵MU1如式（6）所示，同理得滑轨的描述矩阵MU2为：

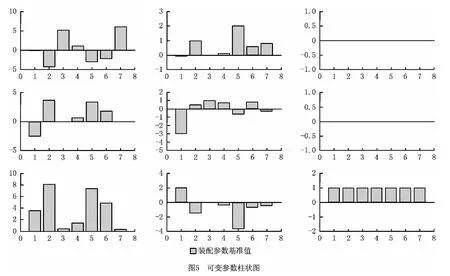
由式（4）得从床身到滑轨的装配过程矩阵基准值

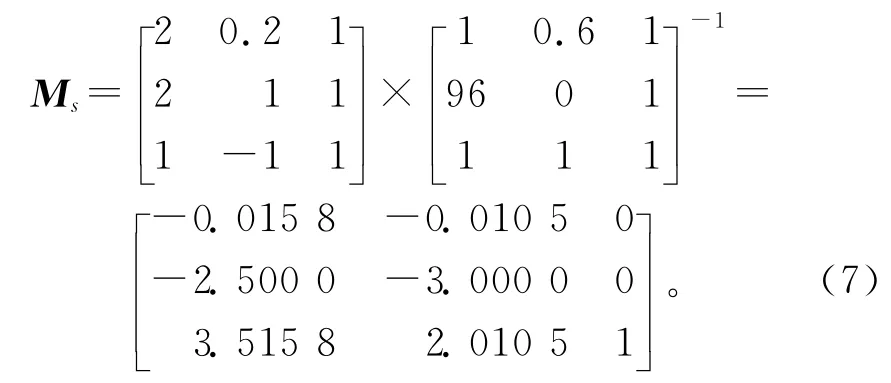
3.2 仿真求解

依据前述原理，基于MATLAB 开发了专用的计算软件，其界面如图7所示。该软件能够实现各模块间的叠加分析，求解出具体方案并进行验证。

首先，按照式（7）的算法求出Msi，将数据填入系统，求出所有的基准值；然后，逐步调整各个装配过程描述矩阵的值（如图7），将导轨的装配过程描述矩阵第2行第2列YT 从-3修改为-2.95，其等效行为为缩短导轨纵向装配的周期；最后，解得铣头的装配状态描述矩阵参数，XYZ 三向偏移总体小于0.8，自由度绝对值最终接近4（如图8），并且与理想状态（虚线）对比可知，它随装配过程稳定增加，求解成立，属于可取解范围，即在装配过程中做出各个对应参数的装配调整是可取的解。

3.3 仿真解的评估

图9所示为求解获得的多指标示意图，图10所示为理想状态的值。对比图9与图10的数据可直观看出，经过调整后的装配参数除YQ 和XT 项之外都略有缩减（如表2），说明在满足装配要求的前提下，经过调整后的装配方案优于调整前的装配方案。与原本理想的装配方案对比可知，在装配过程中，略为降低立柱X 向螺栓装配的精度、提高横梁向的装配精度、增加铣头X 向的装配时间等一系列调整，可以在机床误差指标接受范围内得出一个使装配工作整体更为节约的方案。

此外，通过叠加柱状图（如图11）可以看出，优化后大于基准值的情况只有一处较为明显（方框标出），大多数变化均小于基准值。同时，如图12a和图12c所示，优化后Q，T，C 三者的整体状态图中也没有显示超出数据范围，说明优化调整处于合理区域。

表2 重型数控机床部件的特征矩阵对比表（无量纲）

4 结束语

本文建立了包含精度、周期及其相关系数三项指标在内的龙门机床装配解决方案，基于多体理论建立了龙门机床结构数学模型，提出一种面向龙门机床的基于多体系统的预估优化方法，基于MATLAB开发了专用工具，实现了装配方案的预估优化，利用多指标面积图示反映了优化效果。本装配方案的预估优化为龙门机床的虚拟装配提供了方法，从而为提高龙门机床质量和性能提供了重要的理论依据，具有重要的理论意义和应用价值。本文所涉及的预估优化方法在实际应用时还需要进行深入、细致的研究，这将在以后的工作中进一步探索。

［1］WEI Zhe.Theory and method of complex mechatronical product design driven by performance and application in large scale injection moulding equipment［D］.Hangzhou：Zhejiang University，2009：25-45（in Chinese）.［魏 喆.性能驱动的复杂机电产品设计理论和方法及其在大型注塑装备中的应用［D］.杭州：浙江大学，2009：25-45.］

［2］XING Deqiang.Study on method of performance driving design for complex mechanical product and typical application［D］.Tianjin：Tianjin University，2010：27-47（in Chinese）.［邢德强.复杂机械产品性能驱动设计方法及其典型应用研究［D］.天津：天津大学，2010：27-47.］

［3］WANG Yong，LIU Jihong.Assembly unit partitioning for collaborative assembly planning［J］.Journal of Mechanical Engineering，2009，45（10）：172-179（in Chinese）.［王 永，刘继红.面向协同装配规划的装配单元规划方法［J］.机械工程学报，2009，45（10）：172-179.］

［4］LIU Zhenyu，TAN Jianrong.Research on process oriented assembly modeling in virtual environment［J］.Chinese Journal of Mechanical Engineering，2004，40（3）：93-99（in Chinese）.［刘振宇，谭建荣.面向过程的虛拟环境中产品装配建模研究［J］.机械工程学报，2004，40（3）：93-99.］

［5］LIU Jianhua，BAI Shuqing，DUAN Hua，et al.Computer aided assembly process control method for manual assembly［J］.Computer Integrated Manufacturing Systems，2009，15（12）：2391-2398（in Chinese）.［刘检华，白书清，段 华，等.面向手工装配的计算机辅助装配过程控制方法［J］.计算机集成制造系统，2009，15（12）：2391-2398.］

［6］WANG Junfeng，ZHANG Qing，LI Shiqi.Virtual modeling and simulation of large assembly equipment with multi-DOFs［J］.Aeronautical Manufacturing Technology，2011（22）：63-66（in Chinese）.［王峻峰，张 青，李世其.多自由度大型装配工艺装备虚拟建模与仿真［J］.航空制造技术，2011（22）：63-66.］

［7］TSENG H E，WANG Wenpai，SHIH H Y.Using memetic algorithms with guided local search to solve assembly sequence planning［J］.Expert Systems with Applications，2007，33（2）：451-467.

［8］CHRISTIAND J Y.Assembly simulations in virtual environments with optimized haptic path and sequence［J］.Robotics and Computer-Integrated Manufacturing，2011，27（2）：306-317.

［9］DEVIPRASAD T，KESAVADAS T.Virtual prototyping of assembly components using process modeling［J］.Journal of Manufacturing Systems，2003，22（1）：211-219.

［10］CHENG Qiang，LIU Guangbo，LIU Zhifeng，et al.An identification approach for key geometric error sources of machine tool based on sensitivity analysis［J］.Journal of Mechanical Engineering，2012，48（7）：171-179（in Chinese）.［程 强，刘广博，刘志峰，等.基于敏感度分析的机床关键性几何误差源识别方法［J］.机械工程学报，2012，48（7）：171-179.］