基于扩展特征树的三维CAD 模型相似评价

白 静

（北方民族大学 计算机科学与工程学院，宁夏 银川 750021）

0 引言

设计作为人类智慧集中体现的一种创造性劳动，其本质就是对知识的处理和利用。随着三维计算机辅助设计（Computer Aided Design，CAD）系统的推广应用，如今三维CAD 模型已经成为设计知识存储的主要载体之一，为产品设计提供了丰富的可重用信息。如何快速、有效地检索并利用三维CAD 模型及其携带的设计知识，成为工业设计领域普遍关注的热点之一。

传统的三维模型检索方法以模型间的视觉相似性为判断依据，提取并比较体现模型视觉特征的几何形状和拓扑结构，完成模型间的相似比较。典型的工作有基于形状直方图［1-2］、二维视图［3］等几何形状及Reeb图［4］、属性邻接图［5］、拓扑连接图［6］等拓扑描述子的方法。总体来说这类方法具有适用范围广、计算效率高等优点，非常适合三维模型的一般性检索。然而，无论是模型的几何形状还是拓扑结构，其表征的内容均为模型较底层的信息；而在工程设计领域，人们希望检索并重用的三维CAD 模型往往需要符合其设计的上下文环境，满足某种语义相似性，造成现有三维模型检索方法多却无法满足CAD 模型检索需求的现状。

为了更加贴近工程设计领域用户的检索需求，研究者们提出了一系列专门针对三维CAD 模型的检索方法。其中一类方法通过提取并比较模型的质量、材料和粗糙度等产品综合信息，实现模型间的相似比较［7］。因为反映了产品的语义特征，这类方法很符合工程领域检索需求，但是往往需要人工输入模型以外的其他信息，所以存在主观性较强、稳定性不足且难以实现自动化的问题。另外一类方法通过提取并比较三维CAD 模型的加工特征图，完成三维CAD 模型间的相似评价［8-9］。这类方法以加工特征识别为基础，能够较好地实现自动化，同时其提取的描述符能够有效地反映加工阶段的语义信息，因此非常适合于寻找具有相同加工成本、加工工艺等加工需求的三维CAD 模型，但是仍难以满足工程设计阶段的检索重用需求。为此，有学者提出了基于设计特征表征的三维CAD 模型相似评价方法［10］。然而，因为设计特征的定义较为自由，同一模型对应的设计特征模型可能不同，且基于设计特征图匹配的相似比较方法效率也很低，所以这类方法并没有得到很好的应用。

针对现有这些检索方法在支持设计阶段的检索及重用方面存在的不足，本文提出一种基于扩展特征树匹配的三维CAD 模型相似评价算法。该方法利用扩展特征树表征三维CAD 模型的设计信息，利用非精确的树匹配策略实现模型间的相似评价。相对于其他三维模型的相似评价方法，本文算法具有以下优点：

（1）表征能力强 通过对设计特征模型的约束性定义及扩展特征关系的自动识别，确保扩展特征树的稳定性和唯一性，对设计特征模型的表征具有非常积极的意义。

（2）匹配速度快 基于非精确树匹配的三维CAD模型相似评价与传统的图匹配相比较，具有明显的效率优势。

（3）检索结果语义性强 适用于面向产品设计阶段的检索及重用。

1 方法概述

给定一个CAD 模型，该模型包含几何、拓扑和语义三个不同层面的信息。为有效辅助设计人员找到满足其设计重用需求的CAD 模型，需要提取CAD 模型中所包含的设计语义信息。这里，最简单、直观的方式就是提取CAD 模型基于形状特征的描述符。这是因为作为一种具有一定工程意义的几何形状，形状特征能够实现CAD 模型的几何实体和其隐含的语义信息的连接。然而，由于形状特征尤其是设计特征定义的自由度很大，基于形状特征表征的描述符往往难以确保其唯一性，制约了基于形状特征的描述符在CAD 模型检索领域的应用。白静等针对这一问题提出一种扩展特征树的工程零件设计特征模型［11］，该模型能够在一定程度上保证设计特征的唯一性及稳定性。利用该描述符的层次属性及局部属性，白静等将其用于三维CAD模型的局部检索中，以支持可重用区域的有效提取和层次表征，并通过位图索引及树匹配实现多模式的局部检索［12］。本文利用扩展特征树表征整个三维CAD 模型，并提出非精确的树匹配算法及一种自适应的权重分配方案，用以实现三维CAD 模型之间的相似评价，完成三维CAD 模型的全局检索。图1所示为本文方法的整体流程示意图。

2 基于扩展特征树的三维CAD模型表征

2.1 扩展特征树的构建

为使零件的设计特征模型具有唯一性，一种有效的方式就是限定模型表征中设计特征的类型。在扩展特征树的表示中，对模型的设计特征进行了如下限定：设计特征为简单设计特征，包括基本设计特征及由这些基本设计特征组合或按一定规律排布而成的组合设计特征和阵列。另外，为了有效地简化模型表征，在扩展特征树的表示中，将特征间的关系分为两类，一类是依赖与被依赖的关系，对应扩展特征树中的父子关系（如凸台上的孔和凸台之间的关系）；另一类是一种平等关系，包括相交和贴合，作为扩展特征树中兄弟节点的扩展属性加以记录，如图2所示。

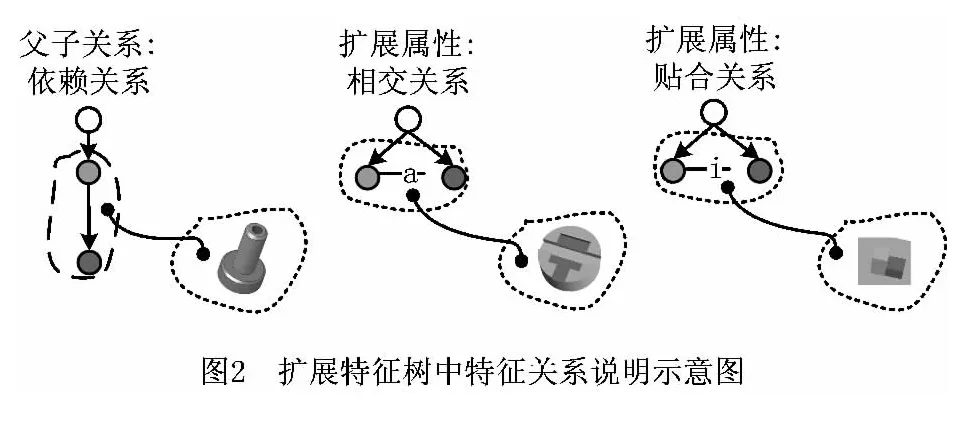
作为示例，图3给出了一个设计特征模型及其对应的扩展特征树。如图3所示，一个三维CAD 模型的扩展特征树可以表示为Q（NQ，EQ，RQ）。其中：NQ为节点集合，EQ为边的集合，RQ为树的根节点。扩展特征树Q 具有以下功能：①通过树的节点集合及其层次属性刻画设计特征模型中不同类型、不同粒度的设计特征；②通过树的边集合记录设计特征间的依赖关系；③通过扩展节点属性、增加兄弟节点信息来记录设计特征间的其他关联关系。也就是说，扩展特征树完整地记录了设计特征模型所包含的设计特征及其关联信息。本文使用文献［11］的方法构建给定三维实体模型的扩展特征树，整体流程如图4所示。

2.2 几何属性的获取

尽管扩展特征树刻画了模型内的设计特征及其关系，但是缺少对模型几何层面信息的表征。为准确刻画被表征模型，本文对扩展特征树中的每一个特征提取了特征尺寸和面数两个几何属性。其中：特征尺寸刻画对应特征的大小信息，由对应特征包围盒的体积决定；面数则刻画对应特征的形状复杂性，由对应特征所包含面的数目决定。需要特别说明的是，本文利用ACIS几何引擎中提供的api＿get＿entity＿box获取对应特征的包围盒，并利用（长×宽×高）计算包围盒体积。作为示例，图5显示了三个包含不同非圆凸台特征的实体模型，表1显示了对应特征的几何属性。可以看出，新增的尺寸和面数两个属性可以帮助人们更好地区分特征类型相同而几何形状不同的特征。

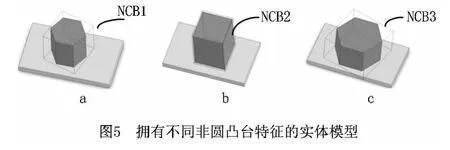
表1 图5所示模型的几何属性

3 扩展特征树的相似评价

在得到三维CAD 模型扩展特征树的表征后，三维CAD 模型间的相似评价问题就转换为扩展特征树间的相似匹配问题。具体地，扩展特征树的相似匹配应遵循以下两点：①查询模型和目标模型并不对等。所有相似比较均以查询模型为出发点，当目标模型缺少查询模型所包含的部分特征时，相似度减少；目标模型若完全包含查询模型中的所有特征，则即使还包含其他特征，相似度也为100%。这样更加符合设计重用过程中的启发式搜索及重用特点。②相似比较中，主体特征对相似度影响大，细节特征对相似度影响小。基于以上观点，下面分别给出精确求解树Q 和T 间相似度的匹配方法，以及本文所采用的更加高效的匹配和相似评价方法。

3.1 精确的树匹配和相似评价

精确求解树Q 和树T 间相似度的算法包括三步：①查找树Q 和树T 间的所有匹配方案；②计算每一个匹配方案的相似度；③计算树Q 和树T 的相似度。下面分别给出各步骤的详细算法。

3.1.1 查找树Q 和树T 间的所有匹配方案

由检索需求可知，树Q 和树T 间的匹配f 是树Q 在树T 中满足以下两个条件的嵌入［13］：

（1）保持父子关系，即对任何节点u 和v，（f（u），f（v））∈ET当且仅当（u，v）∈EQ。

（2）保持节点的层次属性及粗层次的类型属性，即对任何节点u∈NQ且f（u）∈NT，有depth（u）=depth（f（u））∧CoarseType（u）=CoarseType（f（u））。其中：函数depth（u）表示节点u 在特征树中的深度值；CoarseType（u）表示节点u 的粗层次类型；“∧”表示“且”运算。

基于上述定义，求解树Q 和树T 间所有匹配方案的算法步骤如下：

步骤1 利用树嵌入的求解算法［13］获得树Q和树T 之间的所有嵌入方案。

步骤2 以节点粗层次的类型和节点深度必须相同为限制条件，删除部分不满足要求的嵌入方案，获得最终的匹配方案。

3.1.2 计算每一个匹配方案的相似度

给定树Q 和树T 之间的任一个匹配方案f，其相似度定义为该匹配方案中所有匹配树上的节点对的相似度加权和

式中：w（u）为节点u的权重，表征节点对u 和f（u）间的相似度在整个相似评价中的权重；SimilarityOfNodePair（u，f（u））为节点对u，f（u）间的相似度。下面分别给出详细的计算方法。

（1）节点权重的计算

由匹配方案f 的相似度计算公式（式（1））可知：对于给定的匹配方案f，设定不同的节点权重取值方案就会得到不同的相似度度量结果，合理权重的取值方案对获得合理、准确的相似度度量至关重要。分析CAD 模型检索的特点，一个合理的权重取值方案应遵循以下三条原则：

1）树Q 中深度相同的子树权重相等。设ST 为树Q 中的一棵子树，其权重w（ST）可以通过表达式计算。如果子树ST1和ST2满足depth（RST1）=depth（RST2），则w（ST1）=w（ST2）。这条原则旨在保证CAD 模型中两个相同粒度的子区域在CAD 模型的相似度量中占有同等重要的地位。

2）对于任何子树ST，其根节点在该子树中占有的权重只与该子树的高度有关，即子树越高，根节点的权重越小。这条原则很容易理解，因为子树越高，该区域包含的细节信息就越多，在整棵子树权重一定的情况下，根节点占有的份量应该越小。

根据以上三条原则，给定节点对u 和f（u），其相似度在整个匹配方案f 的相似度度量中的权重w（u）可以通过以下步骤计算：

步骤1 令子树CT=树Q，则有w（CT）=1。

步骤2 计算子树CT 的根节点RCT的权重，有w（RCT）=w（CT）×γ。其中γ 是子树CT 的根节点在该子树中的权重因子，由子树CT 的高度值决定，具体的取值可根据需要给定。本文中γ=0.5+0.5×0.6（h-1），h取树的高度。当h=1时，γ=1.0；h=2时，γ=0.8；h=3时，γ=0.68；γ 的值随h 的增加而减小，且永远大于0.5，符合扩展特征树匹配的要求。

步骤3 计算子树CT 的子孤立真子树STi的权重，有（RCT），其中Nc（RCT）为子树CT 的子孤立真子树的数目。将CT 的子孤立子真子树STi依次入栈Un-SolvedSubtree。

步骤4 如果UnSolvedSubtree 非空，则令CT=POP（UnSolvedSubtree），重复步骤2和步骤3，计算其根节点及其子孤立真子树的权重；否则，如果UnSolvedSubtree 为空，则算法结束，树Q 和树T 匹配方案f 中每一个匹配上的节点对u 和f（u）的权重都已获得。

（2）节点对相似度的计算

节点对u，f（u）间的相似度由节点对u，f（u）兄弟关系的相似程度、特征类型的相似程度及其几何属性的相似程度三部分决定，具体计算方法如下：

式中：Ns（u）和Ns（f（u））分别为节点u 和节点f（u）兄弟关系的数目；St（u，f（u））为节点u和节点f（u）特征类型间的相似度；wr，wn，α和β 分别为特征间关系的相似度、特征类型的相似度、特征体积的相似度以及特征面数的相似度在节点相似度中的权重，可以根据不同的检索需求设置相应的值。

将匹配上的节点对的权重及其相似度代入匹配方案f 的相似评价公式（式（1）），就可以获得匹配方案f 的相似度。

3.1.3 计算树Q 和树T 的相似度

树Q 和树T 的相似度被定义为所有匹配方案对应相似度的最大值，即

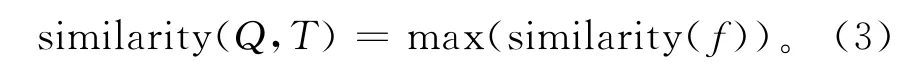
相应地，树Q 和树T 间的最终匹配方案被定义为它们之间拥有最大相似度的匹配方案f。

3.2 改进的树匹配和相似评价

上述精确的树匹配和相似评价方案能够保证获得树Q 和树T 间的最佳匹配方案及最大相似度，且匹配过程非常清晰、易于理解。但是，因为该匹配方案需要通过穷举并比较树Q 和树T 间的所有匹配方案来获得最终匹配方案及相似评价结果，所以计算复杂度高，难以保证检索效率。为此，本文对该匹配方案进行改进，提出一种自顶向下逐层寻找局部最优匹配的方法，获得树Q 和树T 间的最终匹配方案及相似度，从而减小检索代价。具体步骤如下：

步骤1 判断树T 中是否存在树Q 的嵌入。具体地，可以依据文献［13］中介绍的树嵌入求解算法加以判断。

步骤2 如果树T 中存在树Q 嵌入，则通过以下步骤获得最终匹配方案及其对应的相似度量；否则，不匹配。

（1）取树Q 与树T 的根节点，并依据最优二部图求解算法［14］获得树Q 和树T 根节点间的最优匹配方案，将最优匹配对放入匹配堆栈Sm中。这里的最优匹配方案为对应最大相似度的匹配方案，相似度则为利用式（2）计算各个节点间相似度后的累加和。

（2）如果Sm不为空，则取出Sm中的一组匹配节点（v，v′），将其加入最终匹配方案队列Lfm中，取其孩子节点集合并按最优二部图求解算法［14］求解其孩子节点间的最优匹配方案，将所有匹配节点对一一入栈；如果Sm为空，则匹配结束。最终匹配队列Lfm记录了最终匹配方案f，将该匹配方案f 代入式（1），可获得树Q 和树T 间的最终相似度量。

虽然在理论上上述算法无法保证获得树Q 和树T 间的最优匹配方案，但由于在特征树中上层特征在匹配中的作用远远大于下层特征，通常情况下，该匹配算法获得的匹配方案就是最优匹配方案；同时这种自顶向下的匹配方法避免了穷举付出的时间代价，大大改善了匹配效率。

4 算法分析与实验

4.1 算法综合性能分析

针对三维模型的形状描述符及相似评价，学者们提出了一系列评价标准，包括广泛性、唯一性、稳定性、敏感性、高效性、层次性和局部性。以此为基础，对本文所提算法进行综合评价，如表2所示。

表2 基于扩展特征树的CAD模型相似评价算法综合性能分析

（1）广泛性

即形状描述符能够描述所有类型的模型。本文的扩展特征树表征方式并未对被表征模型做任何限定，能够表征所有B-rep表示的三维CAD 模型，适用于CAD 模型检索领域。

（2）唯一性

即在形状和形状描述符间存在一一对应的映射关系，包含两层含义：①如果两个形状相同，则其对应的形状描述符相同；②如果两个形状描述相同，则其对应的形状相同。

本文算法满足含义①，如果两个三维CAD 模型的B-rep表示相同，则其所对应的扩展特征树也相同。忽略人工理解的差异，假定在给出三维CAD模型设计特征的明确定义后，三维CAD 模型设计特征的交互定义具有唯一性，则给定两个三维CAD模型，如果相同，则其所对应的设计特征集合相同，根据扩展特征树的构建算法可知相同特征间的关系也相同，故其对应的扩展特征树相同，且该算法产生的形状描述符对模型的平移、旋转、缩放具有不变性。

对于含义②，本文算法并不完全满足，如图6所示：①当模型A 被模型B 完全包含时，模型A 到模型B的相似度为1，但是模型B 和模型A 并不相同；②当模型A 和模型C拥有相同的特征集合和特征结构、仅是其特征所在位置不同时，本文算法无法有效区分其差异性；③当模型A 和模型D 拥有相同的特征集合和特征结构，其特征尺寸和特征面的数目也完全一致但特征本身形状不同时，本文算法也无法有效区分其差异性。但是，针对设计阶段的重用，以上情况均可通过修改其中一个模型较容易地生成另一个模型，即这种差异性并不影响其设计重用价值，因此该算法在以设计重用为目标的检索中仍是合理、可行的。

（3）稳定性

即三维CAD 模型B-rep表示中的小改动不会造成相应设计特征模型的大改变。给定两三维CAD 模型，如果它们之间存在小的差异，则其对应的设计特征集合中会存在一些不同的局部形状特征，根据扩展特征树的构建过程可知，这些不同的设计特征对应的特征间关系也会有所不同，但是其他特征及特征间的关系仍然相同，体现在扩展特征树中则是：两模型对应扩展特征树间的公共子树与其各自的扩展特征树间的差异都很小，即设计特征模型间的差异较小。

（4）敏感性

即能够检测出不同物体之间的细微差别。本文所采用的扩展特征树通过深层次的叶子节点记录了模型内部小的设计特征，而相同深度、类型特征节点之间，本文又增加了特征“尺寸”和“面数”两个属性来进一步区分，因此本文算法具有一定的敏感性，能够较好地区分模型之间的细微差别。

（5）高效性

即能够高效地计算和比较三维模型的形状描述符。由于在三维模型的检索中，只有查询模型的描述符需要在线提取，其他描述符都可以离线提取，而比较则需要对库内每个模型在线进行一次。因此，比较算法的时间复杂度对检索性能的影响更大。本文扩展特征树构建算法的复杂度为特征数目的多项式时间，而树匹配算法的复杂度也为多项式时间，详细分析如下。

为了方便评价匹配和相似所需时间，假定参与匹配的树均为包含p 个节点的q 叉树，即树中除叶节点外，每个节点都有q个孩子；同时假定树中包含了t个非叶节点，则有p=tq+1。完成一次两树间的匹配和相似度度量所需时间包括以下两部分：

1）判断树T 中是否存在与树Q 匹配的子树的复杂度 由文献［13］可知求解树嵌入的算法复杂度为线性的，即对于包含p 个节点的子树，所需时间为o（p）［13］。

2）确定匹配方案和相似度量的复杂度 如果不存在嵌入，则复杂度为0；否则，复杂度计算如下：根节点的匹配时间为常数1；给定节点对孩子节点间的匹配方案由最优二部图求解算法确定，而最优二部图求解算法的复杂度为o（n3），故给定节点对孩子节点间的匹配时间为o（q3），则两棵树所需时间为1+t（o（q3））=1+o（tq3），又有p=tq+1，故两树匹配方案及相似度所需时间为o（p3）。由以上两步计算可知，一次完整的匹配和相似评价所需时间为o（p）+o（p3），即复杂度为o（p3），匹配效率较高。

（6）层次性

能够建立具有层次性质的形状描述符。显然，基于扩展特征树的表征方式本身就是一种层次性的描述方式，因此能够较好地平衡稳定性及敏感性的双重要求。

（7）局部性

能够对模型局部信息进行表征和比较。显然，扩展特征树中的每一个子树都对应了模型的一个局部区域，因此本文方法具有局部表征能力。

综上所述，基于扩展特征树匹配的三维CAD 模型相似评价算法综合性能良好，适用于CAD模型，具有唯一性、稳定性、敏感性、层次性和局部性，能够在多项式时间内完成相似评价，且匹配效率较高。

4.2 实验与分析

下面验证本文算法。实验环境如下：在Pentium4 1.6GHz CPU，2GB 内存的PC 机上，以Microsoft Visual Studio 2003为集成开发环境，ACIS 13.0为几何造型平台，设wr=0.4，wn=0.6，α=β=0.5。

实验1 两个三维CAD 模型的比较。

图7所示为两个相比较的三维CAD 模型，并按照程序运行情况给出了模型所对应的扩展特征树。表3所示为扩展特征树中各个特征的详细情况。采用本文算法计算这两个模型间的相似度，可得：模型1到模型2的相似度为90%，模型2到模型1的相似度为100%。这里需要说明的是，模型1到模型2的相似度为90%是因为模型1和模型2整体相似，但是模型1 中所要求的部分特征在模型2 中不存在；90%的相似度合理地体现了模型间的整体相似性，同时也捕捉到了彼此之间的差别；而模型2到模型1的相似度为100%是因为模型1包含模型2中的所有特征且几何属性相同，满足启发式检索需求。

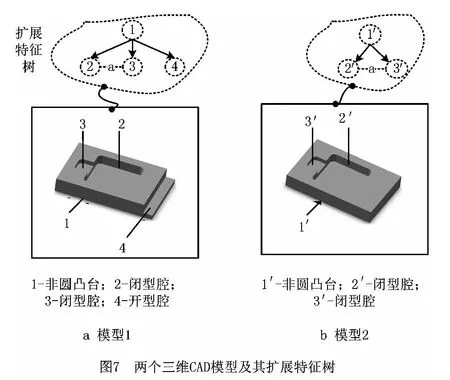
实验2 多个模型间的相似评价。

表4所示为5个不同的三维CAD 模型及其相似度。实验结果表明本文的相似评价算法具有如下特点：①一致性，模型与自身的相似度为100%，同时模型与完整包含其特征信息的模型间的相似度也为100%，与其他模型的相似度小于100%，符合设计重用阶段检索特征。②所计算的相似度不具有对称性。例如模型A 到模型B的相似度为90%，而模型B到模型A 的相似度为100%。这反映了目标模型对查询模型所包含属性的匹配程度，符合设计阶段的启发式检索特征。③相似评价具有稳定性，且计算结果较好地反映了模型设计中的特征及其关系的综合信息。例如：模型A 和模型B 设计较为相似，它们间的相似度远远大于模型A 到模型C，D，E间的相似度；模型C 和模型D 非常相似，只是一些细节设计特征上稍有不同，它们之间的相似度也比较高。

表3 图6中两个三维CAD模型的特征信息

表4 一组三维CAD模型的相似度矩阵 %

实验3 检索效果测试。

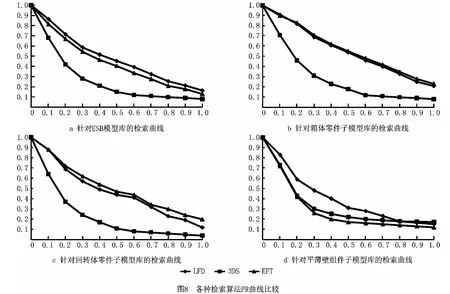
为进一步验证算法的检索效果，本文以Solid-Works 2007为工具，以ESB 模型库为源，建立了一个包含801个边界表示模型、42 个类的模型库，并基于该测试库构建检索结果的PR 曲线。具体地，分别以三维形状分布［1］（3D Shape Distribution，3DS）、光场描述子［3］（Light Field Descriptors，LFD）及本文所提的扩展特征树（Extended Feature Tree，EFT）三种不同检索方法作为测试对象；以ESB模型库及其平薄壁组件（flat thin walled components）子模型库、箱体零件（prismatic parts）子模型库、回转体零件（solids of revolution）三个子模型库为测试库。图8所示为各种算法在相应测试库下的检索PR 曲线，可以看出：①针对整体测试库，EST 算法检索效果明显优于3DS，与LFD 相当；②针对箱体零件和回转体零件子模型库，EST 算法检索效果略优于LFD 算法；③针对平薄壁组件，EST算法效果较差，低于LFD 算法和3DS 算法。分析各子模型库内模型可知：①平薄壁组件子模型库中包含的各模型为薄壁件，特征关系较为简单，但是单个特征往往比较复杂，而EST 算法能够更好地捕捉特征间的关系，但是对相同类型的单个特征描述能力有限，造成其检索效果较差；②箱体类零件和回转体零件内各个特征相对规范，但其特征关系较为复杂，EST 算法能够更好地表征这类模型，同时不受其子特征及特征几何细节信息变化的影响，因此具有更好的检索效果。

实验4 效率测试。

现有的零件库规模较小，零件也比较简单，无法有效地测试算法效率，因此采用随机生成扩展特征树的方法来测试本文算法的效率。实验中，为了测试树的深度和节点数对匹配效率的影响，随机生成深度为2，4，6，节点数为20，30，40直至90 的多个扩展特征树，并记录匹配100次所需的时间。图9所示为实验结果，其中三条曲线分别对应深度为2，4，6的扩展特征树。实验结果表明：①相同深度的扩展特征树，其匹配时间与节点数目成多项式时间增长的关系；②随着树深度的增加，其匹配时间明显下降。因为实际零件中的特征数目一般在50个以内，深度在4层左右，所以以①，②两项观察为依据，可推理出一个包含10 000 个模型的数据库，其匹配时间不足半分钟，即本文算法具有较高的匹配效率，能够支持实时检索的需要。

5 结束语

本文面向设计阶段对三维CAD 模型的检索及重用需求，针对三维CAD 模型的特点，提出了基于扩展特征树匹配的三维CAD 模型相似评价算法。利用扩展特征树刻画三维CAD 模型内的设计特征及其关联关系，完整而有效地表征了三维CAD 模型的设计语义信息；非精确的树匹配算法利用树嵌入的思想及有效的权值分配方案确保相似评价的高效性和有效性，符合设计阶段的启发式检索特征。经过测试，效果符合预定目标。

为进一步提高三维CAD 模型的检索效率，下一步工作将考虑引入合理的聚类算法，实现对库内模型的预先划分，以更加快速、准确地定位可重用模型。

［1］OSADA R，FUNKHOUSER T，CHAZELLE B，et al.Shape distributions［J］.ACM Transactions on Graphics，2002，21（4）：807-832.

［2］ZHANG Ruzhen，WANG Wan，ZHOU Xionghui.Three-dimensional model similarity based on improved shape distribution algorithm［J］.Computer Integrated Manufacturing Systems，2007，13（10）：1928-1933（in Chinese）.［张汝珍，王 婉，周雄辉.基于形状分布算法的三维模型相似性研究［J］.计算机集成制造系统，2007，13（10）：1928-1933.］

［3］CHEN D Y，TIAN X P，SHEN Y T，et al.On visual similarity based 3D model retrieval［J］.Computer Graphics Forum，2003，22（3）：223-232.

［4］BESPALOV D，REGLI W C，SHOKOUFANDEH A.Reeb graph based shape retrieval for CAD［C］／／Proceedings of ASME DETC 2003Computers and Information in Engineering.New York，N.Y.，USA：ASME，2003.

［5］TAO Songqiao，HUANG Zhengdong，ZHENG Tanguang.CAD model retrieval based on attributed adjacency graph matching［J］.Computer Integrated Manufacturing Systems，2011，17（4）：680-687（in Chinese）.［陶松桥，黄正东，郑坛光.基于属性邻接图匹配的三维CAD模型搜索方法［J］.计算机集成制造系统，2011，17（4）：680-687.］

［6］PAN Xiang，ZHANG Sanyuan，ZHANG Yin，et al.3D Model retrieval based topology connection graph［J］.Chinese Journal of Computers，2004，27（9）：1250-1255（in Chinese）.［潘翔，张三元，张 引，等.一种基于拓扑连接图的三维模型检索方法［J］.计算机学报，2004，27（9）：1250-1255.］

［7］TSAI C Y，CHANG C A.A two-stage fuzzy approach to feature-based design retrieval［J］.Computers in Industry，2005，56（5）：493-505.

［8］SEE K Y，HEE J Y，GU K B，et al.Feature-based part similarity assessment method using convex decomposiiton［C］／／Proceedings of ASME DETC 2003Computers and Information in Engineering.New York，N.Y.，USA：ASME，2003.

［9］ANTONIO C，SATYANDRA K G，ABHIJIT D，et al.Machining feature-based similarity assessment algorithms for prismatic machined parts［J］.Computer-Aided Design，2006，38（9）：954-972.

［10］LI M，FUH J Y H，ZHANG Y F，et al.General and partial shape matching approaches on feature-based cad models to support efficient part retrieval［C］／／Proceedings of the 28th Computers and Information in Engineering Conference.New York，N.Y.，USA：ASME，2008：121-130.

［11］BAI Jing，ZHOU Guangping.Design reuse oriented construction of design feature models of engineering［J］.Journal of Computer-Aided Design &Computer Graphics，2011，23（4）：622-632（in Chinese）.［白 静，周广平.面向设计重用的工程零件设计特征模型构建［J］.计算机辅助设计与图形学学报，2011，23（4）：622-632.］

［12］BAI Jing，GAO Shuming，TANG Weihua，et al.Design reuse oriented partial retrieval of CAD models［J］.Computer-Aided Design，2010，42（12）：1069-1084.

［13］PEKKA K.Tree matching problems with applications to structured text database［D］.Helsinki，the Netherlands：the Netherlands University of Helsinki，1992.

［14］MUNKRES J.Algorithms for the assignment and transportation problems［J］.Journal of the Society for Industrial and Applied Mathematics，1957，5（1）：32-38.