巧妙绘制三等径相切圆

陈海凡，胡木林

（广东省技师学院，广东 博罗 516100）

1 问题提出

如图1 已知矩形ABCD 中，AB=40，BC=28，圆O1、O2分别和矩形两直角边相切，圆O3与圆O1、圆O2、线CD 相切，并且三圆半径相等，要求画出图形。

经常和数控竞赛打交道的朋友都知道，国内的数控竞赛一直都是和CAXA 软件公司合作，所以比赛场地就只有CAXA 软件，因为该软件没有约束和缩放等功能，要画出该图形不容易，该题目曾考倒了不少选手，笔者是利用数学和该软件里面的公式曲线方程来巧妙计算出该圆半径的。

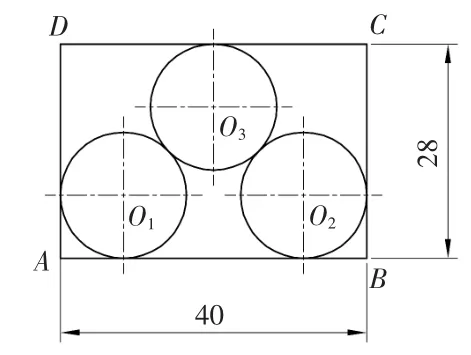
图1 三圆等半径

图2 关系图

2 解决方法

步骤1：数学计算。由图2 的关系图我们可以看出有如下关系：

由式（1）展开后得400-40r+r2+784-112r+4r2-4r2=0

步骤2：公式曲线。要想解出r 值，当然可以采用求根公式法，但是要通过化简、求根等，比较复杂并且很容易出错，在此向大家介绍一种比较简单、准确度高的方法，就是利用CAXA 里面的公式曲线功能，将公式：400-40r+r2+784-112r+4r2-4r2=0。演变成变量为t 的公式：

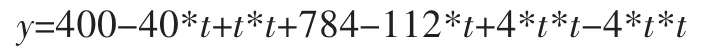
代入CAXA 里面的公式曲线方程如图3，然后便生成图4 的曲线，再通过测量原点1 到点2 的距离便是r值了，因为曲线和X 轴的交点，也就是当y=0 的时候r 的值为原点1 到2 点的距离。

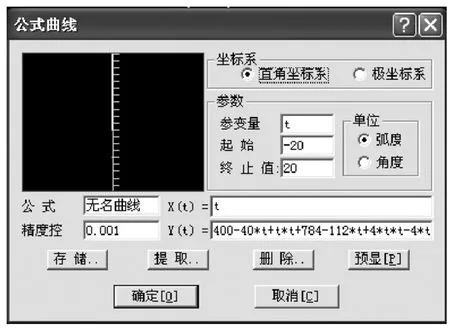
图3 公式曲线

图4 曲线交点

3 结语

通过CAXA 的公式曲线功能，可以解决很多绘图的难题，特别是通过已知求未知，只要是需要通过复杂的数学运算的，通过CAXA 公式曲线功能可以轻松解决。

［1］张安鹏.CAXA 电子图版二维CDA 绘图实例教程［M］.北京：北京航天航空大学出版社，2006.

［2］宛剑业.CAXA 数控车实用教程［M］.北京：化学工业出版社，2005.

［3］范悦.CAXA 数控车实例教程［M］.北京：北京航天航空大学出版社，2007.