基于ABAQUS的单排四点接触回转支承接触分析

郑岩，李庚袁

（合肥工业大学机械与汽车工程学院，合肥 230009）

0 引言

单排四点接触回转支承是可同时承受轴向载荷、径向载荷和倾覆载荷的大型轴承，其结构紧凑、运动平稳且承载能力强，广泛应用于塔式起重机等工程领域。回转支承一旦发生故障，不仅修理费用高，还会造成长时间的非计划停机，严重影响整机甚至整条作业线的生产效率。回转支承失效形式主要为滚道损坏和断齿［1］，其中滚道损坏的比例达98%以上，滚道损坏与其应力场密切相关。因此，滚动体滚道接触处的应力场成为科研人员研究的焦点［2］。

赫兹理论是解决接触问题的经典方法，用赫兹理论可以求出回转支承承载时的接触应力和变形［3，4］。但有文献指出，赫兹点接触理论用于此类问题的求解要求沟曲率半径系数f ≥0.54［5］，而单排四点接触回转支承的f 一般在0.52～0.54 之间，故使用赫兹理论求解回转支承的接触分析存在一定误差。

有限元法是解决工程问题的另一种有效途径。接触问题是一种高度的非线性问题，ABAQUS 有限元软件在处理非线性问题方面有着突出优点，本文将通过ABAQUS 软件对单排四点接触回转支承接触问题进行求解，以得到滚球与滚道接触区的应力分布与变形情况，并与赫兹理论解进行对比。

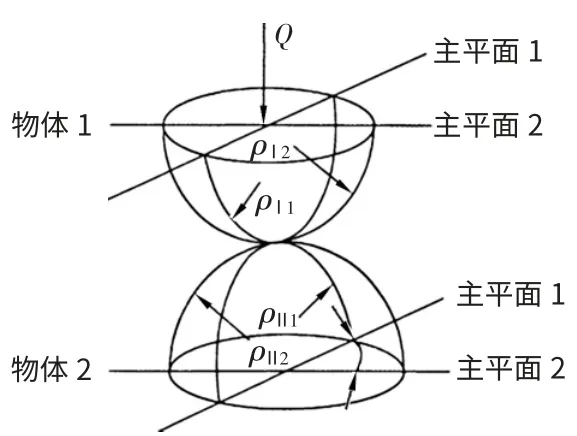
图1 2 个相互接触物体的几何关系

1 回转支承的赫兹接触理论计算

1.1 赫兹接触理论

赫兹接触理论假设材料均质，接触区的尺寸远远小于物体的尺寸，作用力与接触面垂直，接触区内不存在摩擦，且为弹性变形。

2 个相互接触物体的几何关系见图1。其中，平面1 和平面2 为相互垂直的平面，在求解赫兹接触问题前要先说明2 个定义，即曲率和Σρ 和曲率差F（ρ），其定义如下：

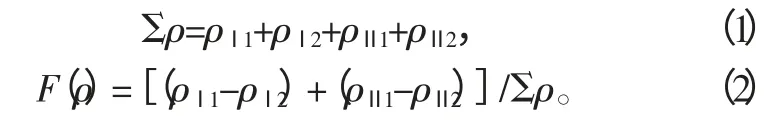
式中，ρⅠ1、ρⅠ2分别为物体1 在平面1 和平面2 中的曲率；ρⅡ1、ρⅡ2分别为物体2 在平面1 和平面2 中的曲率。

根据赫兹接触理论，接触椭圆的长轴a、短轴b 和最大接触应力Pmax、接触中心位移量δ 分别为：

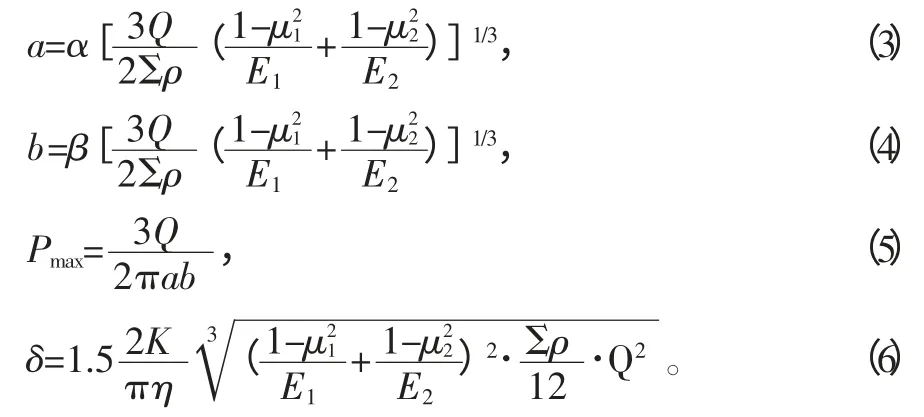
式中，μ1、μ2分别为物体1、物体2 的材料泊松比；E1、E2分别为物体1、物体2 的材料弹性模量；α、β 为与F（ρ）有关的无量纲量［6］；Pmax为最大接触应力；Q 为法向载荷；2K/πη 可由F（ρ）查表得到。

1.2 回转支承接触问题的赫兹理论解

本文以010.20.200 型回转支承为研究对象，分析其在最大轴向载荷Fa=550 kN下的变形和应力场。回转支承的简化模型如图2所示，由内圈、外圈和24个滚动体组成，滚动体直径为20 mm，圆形滚道，滚道半径为10.4 mm，初始接触角为45°，材料的弹性模量为2.1×105MPa、泊松比为0.3。

图2 回转支承简化模型

对单排球式回转支承施加的轴向载荷Fa，由所有滚动体均等地承担，因此，接触处的法向载荷Q 可通过式（7）获得：

式中：Z 为滚动体的个数；α为滚动体和滚道的接触角。

由式（1）～式（7）可得表1 所示的回转支承的内圈与滚动体和外圈与滚动体之间的接触椭圆长轴a、短轴b 和最大接触应力Pmax。

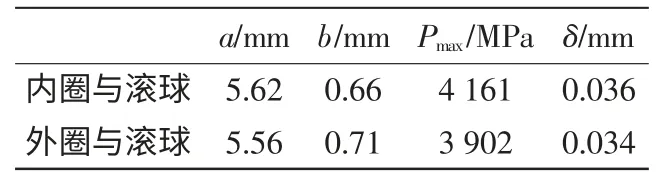
表1 010.20.200 型回转支承接触参数

2 回转支承的有限元计算

2.1 有限元模型的建立

考虑到模型的对称性，本文建立了010.20.200 型回转支承1/24 模型，通过施加循环对称边界条件来模拟整个模型的接触分析，以减小计算模型，减少计算时间。模型材料属性为各向同性，内圈的内环节点约束xyz 自由度，外圈承受的轴向载荷等效成18.24 MPa 的表面压力P，在滚动体与内外圈之间建立2 对接触对，接触属性设置为硬接触和有限滑移，内外圈两侧面添加循环对称边界。完成后网格模型及边界条件如图3 所示。

为保证接触区应力结果的准确性，模型网格全部采用六面体单元，单元类型为C3D8I，对接触区网格进行局部加密，网格大小约为0.05 mm，相当于接触椭圆短半轴的1/13，完成网格划分的模型单元数为265 328，节点数为278 206。网格模型剖面如图4 所示。

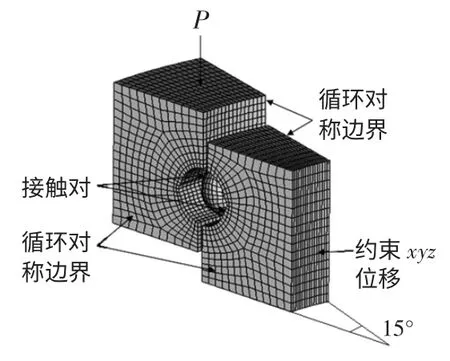
图3 边界条件和载荷示意图

2.2 有限元计算结果

经ABAQUS 求解结果显示，模型最大应力出现在滚球与内滚圈接触处，最大Mises 等效应力值为2 577 MPa，内滚圈沿对称面剖分后的模型应力云图如图5 所示。

ABAQUS 分析结果与赫兹接触理论计算结果对比如表2。

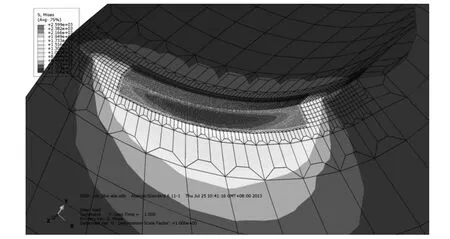
图5 内圈局部剖视等效应力云图

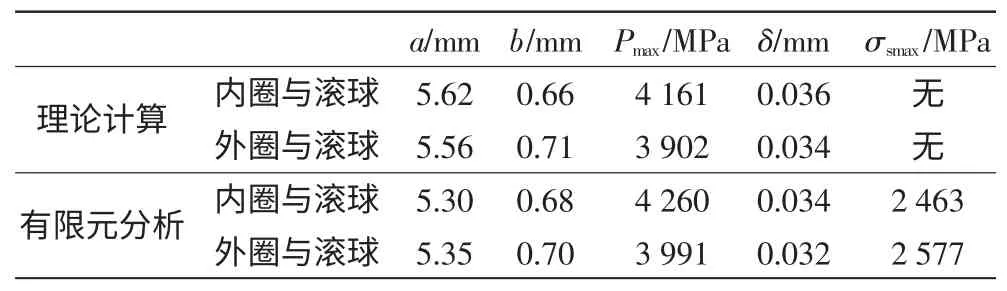
表2 理论解与有限元解对比

对比有限元分析结果与赫兹接触理论计算结果可以发现，两者在接触椭圆形状、最大接触应力以及接触中心变形量的结果上近似相等。赫兹接触理论并没有给出最大等效应力出现的位置，回转支承制造时要求滚道表面淬硬层深度为3～5 mm，主要考虑到滚道接触区应力最大值出现在该位置［6］。本文利用有限元解得到的应力最大值位于滚道表面以下0.43 mm 处，与3～5 mm 相差甚远，而本文中模型在3 mm 处的应力值仅为0.43 mm 处的36%。此外，相比赫兹接触理论计算结果，有限元分析结果更为全面，可以得到滚球与滚道接触区所有位置的应力值和变形量。

3 结论

1）通过赫兹接触理论和有限元法分别求解了单排四点接触回转支承滚球与滚道接触区的应力分布与变形量，二者结果近似相等，相比赫兹接触理论，有限元法对接触区的应力及变形的求解更为全面。

2）滚道最大应力值距滚道表面的距离远低于3～5 mm的淬硬层深度。

［1］刘雪霞.回转支承承载性能分析方法研究［D］.大连：大连理工大学，2011.

［2］Pandiyarajan R，Starvin M S，Ganesh K C.Contact Stress Distribution of Large Diameter Ball Bearing Using Hertzian Elliptical Contact Theory［J］.Procedia Engineering，2012，38：264-269.

［3］Ricci M.Static load distribution in ball bearings［C］//Proceedings of the 40th Aerospace Mechanisms Symposium，NASA kennedy Space Center，2010：12-14.

［4］Lazovic T，Ristivojevic M，Mitrovic R.Mathematical model of load distribution in rolling bearing ［J］.FME Transactions，2008，36（4）：189-196.

［5］吴飞科，罗继伟，张磊，等.关于Hertz 点接触理论适用范围的探讨［J］.轴承，2007（5）：1-3.

［6］徐立民，陈卓.回转支承［M］.合肥：安徽科学技术出版社，1988.