基于模态分析的振动筛结构修改研究

刘选民

（江苏建筑职业技术学院，江苏 徐州 221116）

0 引言

振动筛被广泛应用于煤矿生产的许多环节，为了提高筛分效率，需要对其进行局部修改，在结构局部修改之后如何快速求出结构的动态特性，以满足生产需求，是结构修改再分析所要研究的问题，也是对振动筛进行优化设计所要研究的问题，结构修改研究就是为了不断优化振动筛结构，满足使用者要求，延长振动筛寿命，提高筛分效率。

1 结构修改

对振动筛进行结构修改是要解决两个方面的问题，一是当筛体的结构参数因需要作某些改变时，根据其质量矩阵、刚度矩阵和阻尼矩阵的改变量（ΔM、ΔK、ΔC）求结构的动态特性（特征值和特征向量）的改变Δλ 和Δφ；二是希望通过某些结构参数的改变使系统特性满足预定的要求，即已知结构动态特性的改变量Δλ 和Δφ 来求出结构物理参数的改变量ΔM、ΔK、ΔC。

1.1 固有频率的预测

在已知修改量后，如何求得结构动态特性的变化，瑞利能量法给我们提供了一种简便的方法，它是基于假设振型的一种估计系统固有频率的近似方法，基本公式是：

从式（1）可知，如果给某阶振型以适当估计，就可以计算出固有频率。

在结构小修改的前提下，如果以｛Φoi｝作为｛Φi｝的近似，则由式（1）可以方便地求出pi。此时：

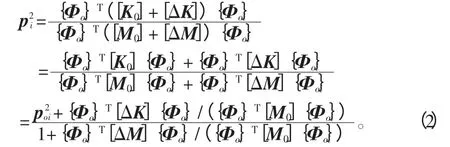
显然，利用式（2），可方便地求出结构修改后固有频率的估计值。

1.2 响应的预测

在线性振动理论中，计算结构动态响应的一般方法是振型叠加法，它的基本公式是：

其中，［ΦN］为正则化振型矩阵。

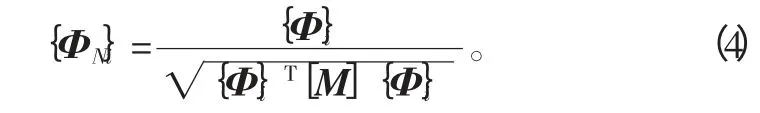
由此可知，只要pi、｛Φi｝及［M］已知，经过一系列矩阵乘法运算和代数运算，就可以求出结构的动态响应。

2 结构修改分析

结构修改分析最基本的方法也称为双模态空间分析法，原理如下：结构物理参数矩阵为M、K、C，对应的修改量为ΔM、ΔK、ΔC，修改后结构的振动微分方程为

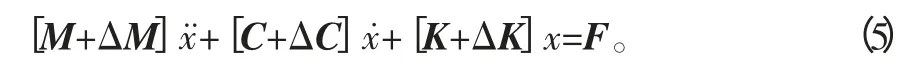
设结构为黏性比例阻尼系统，原结构模态矩阵φ 记为φ1，做坐标变换

φ1为各列构成模态坐标系I 的完备正交基，y 为结构各点在此坐标下的向量。将式（6）代入式（5），考虑到φ1关于M、K、C 的正交性，有：

求解式（7）特征值问题，可以得到特征值λi′和特征向量φi2，φi2构成模态坐标系II 的完备正交基，模态矩阵为φ2。再做变换

代入式（7）得

由式（6）和式（8）可得

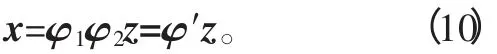
式中φ′＝φ1φ2为修改后结构的模态矩阵。同时求解式（9）代入式（10）得到修改结构的动力响应。

根据上述分析方法，在已知结构模态参数mi、ki、ci、φ后，可以求得结构修改后的模态参数、M2、K2、C2。

3 修改实例

下面以三自由度系统修改为例来说明利用频率响应函数方法进行结构修改的过程。为计算方便，设m1=m2=m3=1 kg，k1=k2=k3=100 N/m，阻尼取为模态阻尼ξ10=ξ20=ξ30=0.035。

根据多自由度系统振动的微分方程：

可知，系统的无阻尼固有频率为

图1 修改后的系统

现对原系统进行修改，在弹簧k1处加一弹簧k0，在弹簧k4处加一弹簧k0，在m3上加一集中质量m0，修改后的系统如图1 所示。

由于仅第一个和第三个自由度被修改，所以位置矩阵

刚度矩阵的增量为

质量矩阵的增量为

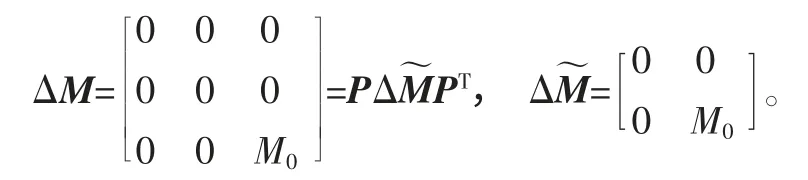
取k0=200 N/m、m0=0.1 kg，利用：H＝H0－H0PPTH0P）－1PTH0。

式中H0为修改前的频响函数矩阵，为m×m 阶对称矩阵。可以计算出修改后的频响函数矩阵，并得到修改后系统的固有频率为

4 结语

作为典型的板梁结构，振动筛的动态特性很复杂，在对其结构修改时，需要有简洁方便的预测方法，利用频响函数法可以进行修改后模态参数的快速识别，相对容易得到修改后的频响函数和振型矩阵。对于具体工况的振动筛，使用者有具体的要求，我们应根据振动理论和实验，不断改善振动筛特性，满足使用者的要求。

［1］闻邦椿，刘风翘.振动机械的理论及应用［M］.北京：机械工业出版社，1982.

［2］曹树谦，张文德.振动结构模态分析［M］.天津：天津大学出版社，2001.

［3］唐友刚.高等结构动力学［M］.天津：天津大学出版社，2002.

［4］吴丽娟，李惠杉.直线振动筛振动特性分析［J］.机械工程师，2004（8）：45-47.

［5］赵华.振动筛激振器的有限元分析及结构改进［J］.煤矿机械，2012（5）：100-102.

［6］张楠.基于动态优化设计方法振动筛设计的研究［J］.煤矿机械，2008（3）：12-15.

［7］刘选民.振动筛结构动力修改的研究［J］.煤矿机械，2009（12）：56-57.