基于Rasch理论的计算机模型教学测验的设计与应用 *

韦斯林，[美]柳秀峰，王祖浩

(1.杭州师范大学 材料与化学化工学院， 浙江 杭州 310036；2.美国纽约州立大学 布法罗分校，纽约 布法罗；3. 华东师范大学 化学系，上海 200062)

基于Rasch理论的计算机模型教学测验的设计与应用*

韦斯林1，[美]柳秀峰2，王祖浩3

(1.杭州师范大学 材料与化学化工学院， 浙江 杭州 310036；2.美国纽约州立大学 布法罗分校，纽约 布法罗；3. 华东师范大学 化学系，上海 200062)

该文针对当前国内外基于计算机模型的教学测验研究较为滞后的现状，运用Rasch理论及测量设计“四基石”模型，以1600名中、美中学生为对象，通过两轮实证研究，探讨计算机模型教学测验设计的方法、过程。研究结果表明，Rasch理论及“四基石”模型能有效指导计算机模型教学测验的开发、修订，优化测验的质量，为我国相关领域的研究提供有益的启示和借鉴。

计算机模型；Rasch模型；教学测验；科学教育

一、引言

针对学生对科学兴趣日益下降、科学学习只注重死记硬背而不求甚解的现象，学界强烈呼吁科学教育中采取新的方式以激发学生学习动机、促进积极探究、深刻理解科学概念、过程，其中一个重要举措是计算机模型的运用[1]。计算机模型是以计算机为介质对事物、现象、事件、过程或系统的一种可视化表征。它们呈现、仿真自然现象，尤其是常规手段难以进行的实验及复杂系统，学习者可以进行操作、观察，从而描述、解释、预测现象，进行深度科学思维加工。计算机模型运用于学科教育中源于人们对人类学习、认知研究的发展[2]。大量的研究已充分表明，计算机模型对帮助学生合理建构事物的心理表征、促进知识的理解及概念转变、发展高阶思维、训练模型方法及提高建模能力具有重要的意义[3]。随着国际课程改革的不断推进，计算机模型越来越广泛地运用于大中小学各科课堂中，成为当今科学教育研究的一个重要趋势。

随着计算机模型在科学教学中的广泛运用，基于计算机模型的学习评价自然就成为亟待解决的问题。然而，纵观当前国内外科学教育中计算机模型研究的现状，基于计算机模型的学习测评研究显得十分滞后。这既制约了计算机模型的推广，也降低了学生学习的效果。鉴于此，本研究试图探索科学教育中如何设计、实施基于计算机模型的教学评价，重点从方法论层面上讨论基于计算机模型的测验的开发、检验及修订，从而为相关研究提供思路和启示。本文以“物质”概念为例加以具体阐述，具有重要的理论和实践指导意义。

二、Rasch 模型

本研究中教学测验的设计主要以Rasch测量理论为指导。Rasch模型是丹麦数学家乔治·拉希(Georg Rasch)上世纪60年代提出的一种基于概率的测量模型[4]。他认为，被试对某个项目的反应存在着一个数学关系，被试能力与项目难度之间的差异决定了其正确作答的概率。被试能力越高，答对越容易题目的概率就越高；反之，被试能力越低，答对越难题目的概率越低。被试答对某道题的概率(P)与被试能力和题目难度之间的差距(Bn-Di)的相互关系如下页图1所示。

Rasch模型根据学生在一系列项目上的反应运用极大自然法估算出被试能力(Bn)及项目难度(Di)。Rasch测量具有如下优点：(1)测量分数是等距的，Rasch模型将原始分数转换为Logit分，分数真正等距，可以进行各种运算；(2)被试能力和项目难度相互独立，能力估计不受测验难度影响，难度估计也不受能力大小影响；(3)能力和难度并不是直接观测的，是根据被试在一系列项目上的反应通过数学模型进行估算、预测得到的[5]，提高了测量准确性；(4)被试能力和项目难度使用同一把量尺，使得数据具有可比性。Rasch模型的这些特点正是克服了经典测量方法的局限，对建构有效测量具有重要的指导意义。

图1 P与 Bn-Di 的关系

要使Rasch模型能更好地估计能力与难度，测验要满足单维性、局部独立性假设[6-8]，使测验数据更好地拟合理论模型。因而测验需要进行严格的设计、实施、修正和检验。Wilson(2005)基于Rasch及项目反应理论提出的测量建构“四基石”模型(如图2所示)[9][10]，为测验的开发与实施提供了方法论，至今已被广泛运用于大量研究中。

图2 测量建构“四基石”模型

三、研究过程

1.建构学习进程

学习进程(Learning Progressions)是关于学生某一学习领域在一定时间内随时间一步一步发展变化的描述。它由从低到高、前后连贯一致的若干水平组成，有效揭示了学生学习进步的路径，为课程、教学和评价提供了坚实的理论基础[11-15]。借助“学习进程”，可以清晰描绘出测验的理论结构及行为表现，使得项目的内容、水平设计更合理、有效。本研究以“物质”概念理解为例，基于大量文献[16-23]，建构了中学生物质概念学习进程(如图3所示)，并对各水平做进一步的描述[24]。由于研究的对象主要是初三、高一学生，因此主要涉及水平1-3。

2.开发计算机模型

图3 中学生物质概念学习进程

笔者以NetLogo为主要工具，开发系列化学计算机模型。NetLogo是由美国西北大学Uri Wilensky团队开发的基于多代理的建模环境[25]，适合于建模复杂系统及其随时间演化。由于它突出宏观现象、微观、符号的联系，深受科学研究及教育领域广大学者的青睐，至今已经广泛运用于物理、化学、数学、计算机、生物及人文科学等领域中。图4是我们基于NetLogo建模环境开发的“酸和碱”模型的操作界面。学生可以操作界面上的按钮，控制、改变系统相关变量(如物质数量、温度)，观察物质微粒的相互作用(中间窗口)以及有关性质的变化(如微粒数、PH值)。本研究中，针对“物质”概念理解，开发了化学反应、溶液、酸和碱3个模型。

图4 “酸和碱”NetLogo模型界面

3.编制测验项目

针对每个计算机模型，编制题目。每套测验由18个道题组成，其中15道选择题、3道问答题。选择题分别指向物质概念学习进程的1-3水平，问答题答案开放，要求学生根据自己的理解作答。下面是“酸和碱”测验中的两则例子：

例1：(选择题)当拖动酸滑杆中的滑块于某一位置，然后点击“setup”和“go/stop”按钮，此时中间视窗所代表的是 。

A. 单质 B.纯净物 C. 混合物

例2：(开放题)请用文字及图画描述盐酸与氢氧化钠是如何反应的。

4.设计评分标准

基于物质概念学习进程(如图3所示)以及学生的回答，将答案分为具有本质差异的不同等级，赋以相应分数，并用Rasch模型对评分进行修正。例如，“酸和碱”第17题(“请用文字及图画描述盐酸溶液是怎样的”)评分标准如表1所示。

表1 “酸和碱”第17题评分标准

5.施测与数据分析

根据Rasch测量原理，被试能力分布越广、越具多样性，测验效果越好。考虑到所开发模型及测量工具适用于中外学生，因此，选取中国、美国相似学段学生为测试对象，被试分布如表2所示。测试数据使用Rasch模型软件[26]进行处理和分析。我们根据初测分析结果，对测量工具进行修订，并实施第二次测试，再次进行测验的质量检验。

表2 初测、再测被试分布

四、测验质量的分析

1.整体情况

从表3看出，学生能力平均值为-0.03，与测验难度相当(Rasch模型中通常将测验难度平均水平设为0)，表明测验能很好地匹配学生的能力水平(初测为0.31)。拟合包括加权拟合(Infit，即与模型相吻合的反应赋予更大权重)和非加权拟合(Outfit)，MNSQ即非标准化方差检验，ZSTD即标准化Z、t检验。数据显示，被试、项目的拟合指数都十分接近理想水平(MNSQ越接近1、ZSTD越接近0越好)，说明测试数据与理想模型具有很好的一致性，Rasch模型能很好地估算能力和难度。项目、被试分离度分别为7.16、1.51，一般认为分离指数超过2较好，表明测验能较好地区分被试点能力。信度显示，测验信度都较高，项目信度最理想。

表3 “酸和碱”测验总体统计

2.项目—被试分布

“项目—被试图”(Wright Map)[27-29]将难度、能力放置在同一把刻度尺上，直观地呈现了项目与被试的分布情况。试卷总体难度与学生平均水平几乎一致，能力分布较为均匀。试题难度与预期基本一致，如水平1的AB1、AB2、AB4在底部，水平3的AB11、AB12、AB14、AB15在顶部，水平2的AB6、AB7、AB8、AB9、AB10处于中间。表明所编制的项目的认知水平与理论构想较为吻合。

3.数据—模型拟合

如表4所示，除AB3、AB5、AB11、AB17、AB18的ZSTD的拟合指数(Fit)略超出接受范围，其余Fit指标基本都在接受范围之内。项目—总分相关反映项目难度与试卷总难度的相关性，体现项目对能力的区分效果。大部分项目相关系数在0.30以上，表明总体而言，测验具有良好的区分度。

表4 “酸和碱”拟合检验

续表4

4.一维性

弗朗西斯（Francis）等学者曾通过分析表现教师教学方法的事件，对教师的教学特点和可辨认的模式特征进行描述[18]．类似地，研究者把职前教师的教学“模式”定义为：在教学设计及其模拟教学活动中重复出现的，共同构成其教学方法认识特点的可辨认的特征．根据弗朗西斯等学者提出的“指令性的或者传授式的教学”与“探究式教学”的事件的分类标准，从探究、指令、总结、联系等方面，对职前教师的教学设计方案及微格视频进行分析，得到4类较为明显的教学“模式”（见图2），每种教学“模式”的人数分布情况见表6．

Rasch模型要求测验是一维的(Unidimensionality)，其检验方法是进行主成分分析，即计算主变量被控制后项目在其它可能变量上的负荷值。如图5所示，AB17(A)、AB16(B)超出接受范围(-0.4—0.4)，AB18(C)、AB6(a)略微超出。表明测验具有一维性，这些题目共同反映了学生对物质概念的理解。

图5 “酸和碱”一维性检验

5.评分等级结构

开放题评分标准的合理性可以通过评分等级概率(Catergory Probabilities)结构进行检验。理想地，每个分数都应该有一个明显的“峰”，且覆盖一定区域；随着能力增高，学生有可能得到更高分数。根据概率结构情况，可以考察评分标准的设计是否合理。如第17题最初设计7个等级，等级1、3、5被0、2、4、6所覆盖，表明这几个等级应该合并入其它等级中。第二次测试中调整为5个等级，效果较为理想，表明调整后的分类及评分与理论模型具有更好的拟合效果，评分更合理可信。其它开放题的评分标准也遵循类似的方法进行设置、修订，并取得满意的效果。

五、测验的应用

1.测验的等值化

基于物质概念学习进程所开发的系列计算机教学测验之间由于难度不同，分数无法相互比较和计算。利用Rasch模型可以对测量同一属性的不同测验进行等值化[30]。运用“锚试题”技术，通过在不同测验中设计试题链，利用Rasch模型“同时评估”(Simultaneous Estimation)，可以实现测验之间的等值化。同时，用线性回归方法，可以找出原始分数与0-100Rasch分的对应关系(如表5所示)。这样，使用者不需要运行Rasch模型和计算，利用该表便可直接查出学生原始分对应的100刻度Rasch分。这些分数是等距、可比的，可以进行加减乘除以及复杂的统计。经过等值化，教师可以任意选择某一试题对学生进行测验，不同班级或不同时间使用不同测验，这样便可比较不同班级之间或同一班级不同时间的成绩情况。

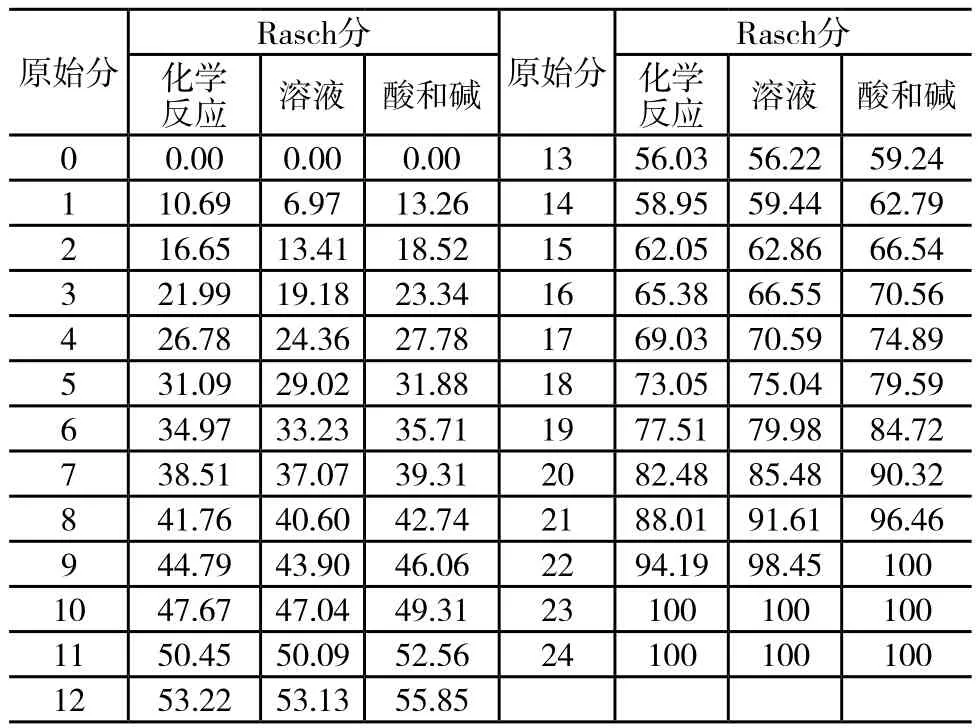
表5 原始分数→Rasch分数的转换表

2.学生概念学习的研究

上述测量设计方法及所开发的测验可以用于学生概念理解的评价与研究。基于各学习水平上的项目的难度，可以计算物质概念理解的学习水平及其范围，从而判断各学生或班级所处的理解水平。例如，针对96名初三、93名高一学生的测验中，其平均分分别为61.21、66.44。由此得知，初三、高一学生均处于物质概念学习水平2，高一高于初三。可见这两个年级学生可以从物质性质与变化认识物质的微粒性，但他们对物质微粒及其运动还不能很好掌握，难以描述、区分原子、分子、离子等微粒。因此，在教学中一方面要注重通过实验现象，帮助学生认识物质性质、变化，更重要是的引导学生对宏观现象的分析、推理，借助模型、微观动画等方法，理解物质微粒相关知识。另外，还可以根据具体教学内容、进度，在不同时间对学生实施不同测验。通过比较学生成绩随时间的变化，可以了解学生知识理解的进步情况，存在的问题，实现学习的及时诊断与过程监控，有助于教师采取有效策略，不断调整教学，促进学生学习持续向前发展。

3.形成性评价

六、总结与展望

本文以“物质”概念理解为例，通过在中、美两国1600余名中学生中开展两轮实证研究，总结提炼出基于Rasch测量理论、技术的计算机模型教学测验设计的一般程序与操作。研究结果表明，这套体系是合理、可行、有效的；所开发的测验工具多个质量指标检验效果良好，根据Rasch模型分析结果所进行的修订测验得到明显改善。因此，研究具有重要的方法论及实践意义。同时，本研究也给我们很多启示：

1.有效实施基于计算机模型的教学评价，揭示学生学习与发展规律，促进课程、教学与评价的一致性。课程、教学与评价相互一致是当今教育的一个重要原则[31]。既然计算机模型逐步广泛运用于科学教学中，了解、监控、预测学生计算机模型学习中其表现及进步情况就显得十分重要。通过测试与反馈，可以最大限度促进学生对科学知识的理解与掌握，优化课堂教学；同时拓展计算机模型新的运用方式，进一步挖掘其教育价值。当然，评价的目标、方式是多样的，可以是诊断性评价、形成性评价或终结性评价。

2.恰当运用科学的教育测量理论、方法设计计算机模型教学测验，提高测评的效果。准确了解学生的学习状况离不开合理、有效的测量与评价。计算机模型环境下，学生学习心理特质具有内隐性、复杂性，因而需要有良好的测验量表、恰当的测量方法，有效揭示学生的心理特征。显然，测量理论、模型的选择十分关键。项目反应理论有效克服经典测量理论的弊端。越来越多实践证明它在有效测评个体能力方面具有显著的价值意义。Rasch 模型被认为是至今唯一普遍用来在人文社科研究中建构类似自然科学中的“基本测量”的测量技术[32]。本研究从多个方面证实了Rasch模型在优化测评质量的重要意义。

3.深入探索现代信息技术与学科学习有效整合的方式与策略，促进学生的学习与发展。技术的真正意义不在于如何运用技术武装教学使教师教得更好，而是如何将技术作为学生学习的重要工具帮助他们进行更有成效的思考，因为学习者不是从技术中获得知识，而是从思考中进行学习[33]。科学教育中，计算机模型作为信息技术与学科内容相整合的一种新方式，在呈现事物的多重表征、模拟疑难实验或复杂系统等方面具有独特的优势。它们可以作为思维工具帮助学习者建构个人知识、进行更有效的思考。然而，这方面研究国内仍显得十分薄弱。尤其是应试教育心理仍比较浓重的情形下，如何将计算机模型有效运用于学科教学中仍值得深入探索。本研究是一种尝试，但一些问题仍需要进一步思考。例如，计算机模型教学测验如何整合入日常及大规模学业测评中，如何将计算机模型测验与课程标准相联系，测验结果如何用于修改、优化教师的教学设计，以及当前教学实际中计算机模型测验的操作性、实效性问题等。

总之，随着计算机越来越广泛运用于科学教学中，人们对计算机模型的研究已经逐渐从宏观理论描述转向微观实证探究，从基于经验的阐释转向基于测量统计方法、工具的揭示，并且日益与现代学习理论紧密结合，这也是信息技术与学科教学整合的重要趋势。本文以现代测量理论为指导，从方法论层面通过具体的实证研究揭示了计算机模型教学测验设计与评价的一般方法、过程，为我国相关领域研究提供有益的借鉴。

[1][2] National Research Council (NRC).Learning Science Through Computer Games and Simulations[M].Washington D.C.:The National Academies Press,2011.

[3][10][30][31] 韦斯林.运用Rasch模型构建基于计算机建模的中学生物质结构认知测量的研究[D].上海：华东师范大学，2011.

[4] G.Rasch.Probabilistic Models for Some Intelligence and Attainment Tests [M].Chicago:University of Chicago Press,1980.

[5][6] X.Liu,W.J. Boone. Applications of Rasch Measurement in Science Education Maple Grove[M]. Minnesota:JAM Press,2006.

[7] X.Liu.Elementary to High School Students’ Growth over an Academic Year in Understanding the Concept of Matter[J]. Journal of Chemical Education,2007,84(11):1853-1856.

[8] X.Liu.Using and Developing Measurement Instruments in Science Education:A Rasch Modeling Approach[M]. Charlotte,North Carolina：Information Age Publishing Inc.,2010.

[9][27] M.Wilson.Constructing Measures:An Item Response Modeling Approach[M]. Hillsdale,NJ:PLawrence Erlbaum Associates,2005.

[11] 韦斯林，贾远娥.美国科学教育研究新动向及启示——以“学习进程”促进课程、教学与评价的一致性[J].课程·教材·教法，2010,30(10):98-105.

[12] T.Corcoran，F.A.Mosher，A. Rogat. Learning Progressions in Science：An Evidence-based Approach to Reform[R].Philadelphia,PA:Consortium for Policy Research in Education,2009.

[13] R.G.Duncan,C.E.Hmelo-Silver. Learning Progressions:Aligning curriculum,Instruction,and Assessment[J]. Journal of Research in Science Teaching,2009,46(6):606-609.

[14] J.R.McGinnis,A. Collins. Special Issue：Learning Progressions [J].Journal of Research in Science Teaching,2009,46(6):605-611.

[15][23] National Research Council (NRC).Taking Science to School:Learning and Teaching Science in Grades K—8[M].Washington,DC:National Academies Press,2007.

[16] X.Liu.Synthesizing Research on Student Conceptions in Science[J].International Journal of Science Education,2001,23(1):55-81.

[17] X.Liu,K.M.Lesniak.Students’ Progression of Understanding the Matter Concept from Elementary to High School [J]. Science Education,2005,89(3):433-450.

[18] X.Liu.Student Competence in Understanding the Matter Concept and Its Implications for Science Curriculum Standards[J]. School Science and Mathematics,2006,k106(5):220-227.

[19] X.Liu,K.Lesniak.Progression in Children’s Understanding of the Matter Concept from Elementary to High School[J].Journal of Research in Science Teaching,2006,43(3)： 320-347.

[20] J.Claesgens,et al.Mapping student understanding in chemistry:The Perspectives of Chemists[J].Science Education,2009,93(1):56-85.

[21] B.Anderson.Pupils’ Conception of Matter and its Transformation [J].Studies in Science Education,1990,(18):53-85.

[22] C.L.Smith，et al..Implications of Research on Children’s Learning for Standards and Assessment:A Proposed Learning Progression for Matter and the Atomic-Molecular Theory[J]. Measurement：Interdisciplinary Research and Perspectives，2006，4(1-2)：1-98.

[24] S.Wei,et al..Using Rasch Measurement to Develop a Computer Modeling-Based Instrument To Assess Students' Conceptual Understanding of Matter[J].Journal of Chemica l Education,2012,89(3):835-845.

[25] U.Wilensky.NetLogo. Center for Connected Learning and Computer-Based Modeling [DB/OL]. http://ccl.northwestern.edu/ netlogo/,2012-12-06.

[26][32] T. Bond，C. Fox. Appling the Rasch Model: Fundamental Measurement in the Human Sciences[M]. Mahwah,NJ：Lawrence Erlbaum Associates, 2007.

[28] B.D.Wright,M.H.Stone.Best Test Design[M].Chicago,IL:MESA Press,1979.

[29] B.D.Wright,G.N.Masters.Rating Scale Analysis [M].Chicago,IL:MESA Press,1982.

[33] D.H.乔纳森.用于概念转变的思维工具——技术支持的思维建模(第三版)[M].上海：华东师范大学出版社，2008.

韦斯林：博士，硕士生导师, 研究方向为学科教育理论与实践、基于技术的学习与教学研究、科学教育测量与评价(silinwei@163.com)。

柳秀峰：博士，教授，博士生导师，研究方向为科学教育、教育测量与评价、信息技术与科学教育。

王祖浩：博士，教授，博士生导师，研究方向为科学学习与能力发展、化学课程研制与评价。

2013年12月25日

责任编辑：宋灵青

Design and Validation on Computer Modeling-based Teaching Assessments by Using Rasch Model

Wei Silin1, Liu Xiufeng2, Wang Zuhao3
(1.College of Material, Chemistry and Chemical Engineering, Hangzhou Normal University, Hangzhou Zhejiang 310036;2.Graduate School of Education, State University of New York at Buffalo, Buffalo New York 14260-1000;3.Department of Chemistry, East China Normal University,Shanghai 200062)

The research on computer modeling-based assessment in science education in China still lagged behind many countries.This study used Rasch measurement-based ‘Four Building Blocks’ approach to develop computer modeling-based assessment for high school students. To validate this method, we conducted three computer modeling-based measurement instruments and used for 1,600 high school students both in China and United States by two rounds. The results show effectiveness of the approach of Rasch measurement-based ‘Four Building Blocks’ as the framework for developing, revising and improving computer modeling-based assessments. Such method can also be applied to many other related contexts.

Computer Modeling; Rasch Model; Teaching Assessment; Science Education

G434

A

1006—9860(2014)07—0139—06* 本文系浙江省教育技术研究规划课题“基于计算机模型的探究性学习环境的实践与探索”(项目编号：JB003)、杭州师范大学项目“学习者为中心的化学计算机模型的设计、应用与国际比较研究”(项目编号：2011QDL35)和“以计算机模型促进知识表征与建模的理论与实证研究”(项目编号：RWWD1316)研究成果。