基于可用性理论的导弹装备使用可用度评估模型研究❋
王鲁彬 崔旭涛 刘军山 张 勇
(1.海军航空工程学院基础实验部 烟台 264001)(2.海军航空工程学院科研部 烟台 264001)
1 引言
战备完好性是指装备在接到作战训练命令时响应作战训练任务的能力[1]。它是部队装备在编实力、装备可用性、训练等因素综合作用的结果,是系统综合保障的总体指标,也是衡量导弹系统战斗力的重要指标之一。使用可用度是装备可用性和战备完好性的概率度量参数,是指某一装备在某种作战使用环境下,在任意随机时刻应召时,可以备便和满意地投入使用的能力[2~3]。
导弹使用可用度是导弹保障部队常用的描述导弹装备可用状态的统计量,是衡量导弹战备完好性的重要数值指标之一。文献[4~8]对装备的战备完好性进行了有意义的研究,但这些研究都是基于装备的概率模型和统计模型,数据来源多为时间概率的统计值,对部队保障工作指导意义不强。据此,笔者结合现役导弹部队实际保障情况,开展导弹使用可用度评估模型研究,结合导弹服役的相关数据,对导弹装备使用可用度进行评估验证,对于实现导弹战备完好性评估与维修保障资源优化配置具有重要意义。
2 使用可用度参数
GJB 451A-2005《可靠性维修性保障性术语》对可用性的定义:“产品在任一随机时刻需要和开始执行任务时,处于可工作或可使用状态的程度。可用性的概率度量亦称可用度。”使用可用度全面考虑了产品的工作时间、待机时间、修复性维修时间、预防性维修时间、保障资源延误时间和管理延误时间,因而最能真实反映产品的可用性特性,是全面评估产品可随时投人使用的有效工具,因此把使用可用度作为度量现役导弹战备完好性的主要指标之一[9~10]。通常,使用可用度被解释为系统完好性,即能在某种作战环境下满意运行的预期百分数。可表示为

式中,n为故障次数,能工作时间为系统运行的时间,或者在待命或关机期间以及能在允许停机时间内进入运行状态的时间。
对概念上的或纸面上的系统/设备,因为无法测量能工作时间和故障停机时间,所以要指明使用可用度不足的原因并找到可能解决的办法,还必须确定各可控的因素平均故障间隔时间(MTBF)、平均修复时间(MTTR)、平均后勤延误时间(MLDT)对能工作时间和故障停机时间的影响。用MTBF、MTTR、MLDT替代“能工作时间”和“故障停机时间”代入式(1),近似得到式(2),这些参数使研制中还处在概念上的或纸面上的系统/设备的使用可用度得以预计,预计使用可用度:

对于冲动式系统(一旦使用后一般不能回收),不能工作的时间概念是无意义的,其大部分时间处在备用、待命或保证的状态,应当发挥作用的时间比较短,为此将冲动式系统的使用可用性量化成在使用时(发射、接通、驱动)的成功次数占使用次数的百分比:

由于使用可用度考虑的因素比较多,因而使用可用度评估比较复杂。研究导弹装备使用可用度需要考虑一系列时间要素。根据GJB451-2005对时间的图解进一步细化可得到导弹装备时间要素图,如图1所示。
3 基于可用性理论的使用可用度评估方法
导弹使用可用度是指导弹能工作时间与能工作时间和不能工作时间之和的比值,从数学的角度来看公式不复杂,然而仅这两项时间与其他很多因素有着密切的联系,而且目前部队描述战备完好性仅从战备完好率这一参数来进行反映,难以满足分析需要,为此,为了分析影响战备完好性因素、建立模型和数学处理需要,本节采用武器系统效能方程中“可用度”的概念,研究导弹装备使用可用度求解方法。

图1 导弹装备时间要素图
3.1 导弹装备可使用状态分析
根据国军标《海军导弹装备质量监控要求通用要求》,导弹装备的质量等级划分为新品、堪用品、待修品、废品(简称新、堪、待、废)四等。根据不同装备使用规定,堪用品可再细分一至三级,待修品可再细分为一至二级。各等级具体定义如下:
1)新品:出厂检验合格,未经过使用,性能检测满足规定要求,储存年限未超过新品规定(有保质期的装备按保质期规定,无保质期的装备按寿命的三分之一(取整)规定),未经过大修和中修,外观完好,符合作战使用要求;
2)堪用品一级:未经过使用,性能检测满足规定要求,储存年限超过新品规定但未达到最后两年,或经过大修、中修且未超过规定修理次数,外观完好,符合作战使用要求;
3)堪用品二级:经过使用或正在使用,性能检测满足规定要求,服役年限未达到最后两年(开机时数、挂飞次数、值班次数未达到规定值),大修和中修未超过规定次数,外观完好,符合作战使用要求;
4)堪用品三级:性能检测满足规定要求,服役年限到达最后两年且未超过最高服役年限(开机时数、挂飞次数、值班次数达到规定值但未超过最高值),大修、中修次数超过堪用品一级或堪用品二级规定,外观基本完好,符合作战使用要求;
5)待修品一级:经过储存、使用,质量状况下降,性能检测参数超差且调整不到规定技术要求或有损坏现象,不能用于作战,需要中修且能修复并有修理价值的;或达到规定预防性维修(中修)条件的;
6)待修品二级:经过储存、使用,质量状况下降,性能检测参数超差且调整不到规定技术要求或有损坏现象,不能用于作战,需要大修且能修复并有修理价值的;或达到规定预防性维修(大修)条件的;
7)废品:超过最高服役年限(开机时数、挂飞次数、值班次数等超过允许值),或大修、中修已达到规定次数又需要大修、中修,或不能用于作战且无法修复或没有修理价值的。
从便于计算和模型构建考虑,仅考虑导弹装备质量等级分为新、堪、待、废四等,即每枚导弹在使用前的可使用状态集合为{“新”,“堪”,“待”,“废”},用{1,2,3,4}表示。分别对应的系统处于该状态的模糊概率设为α1、α2、α3、α4。
3.2 导弹使用可用度计算方法
为保证建立的模型和方法具有通用性,假设导弹在启用时刻有n种可使用状态,可取由好至差的{新,…,废}1×n共n种状态,每种状态都对应导弹处于该状态模糊概率αi,i=1,2,…,n。可用度A表示为
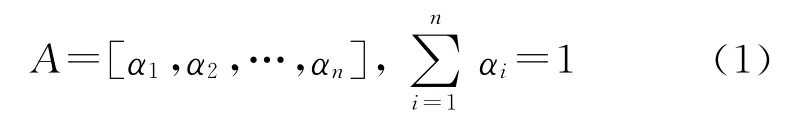
状态集{新,…,废}1×n中各个元素具有外延的不确定性,先建立一个关于状态良好的模糊隶属度μi,i=1,2,…,n,n与之一一对应,则有模糊矩阵:

并且μ1>μ2>…>μn。
当导弹启用时系统处于“新”、“废’这两个极端状态的概率分别为

由于系统仅有这两种极端状态,则有:


由n个密度函数α′i(x),i=1,2,…,n组成,其中x是模糊随机变量。设定系统状态集合中各个状态都具有正态的分布状态,则分布状态集合为:{α1,α2,…,αn},分布密度函数集合为{α′1,α′2,…,α′n}。然后以式(2)中隶属度向量{μ1,μ2,…,μn}作为式(3)中{α′1,α′2,…,α′n}的数学期望集合,且两集合内的元素一一对应。由此可设x的分布密度函数为

式中,βi决定分布形状的参数,μi决定分布位置的参数。
令α*2-α*1=Δα,与式(2)可联解出:

以α*1与隶属度M的元素一一比较,取与α*1之值接近者,α*1≈μi,i=1,2,…,n作为α′(x)分布的位置参数μi。此时Δα=2μi-1,令

这样唯一确定一个密度分布函数。为了计算上的统一,此时令唯一确定分布密度函数中的μi=μ,βi=β,则此分布密度函数为

对此密度分布函数进行分段积分,可得出α向量,如图2所示。

图2 α向量图

其中:
在缺陷分析中可以使用统计方法对收集的缺陷进行分类、汇总。基于不同的缺陷属性,根据需要统计缺陷分布情况,利用统计结果分析缺陷产生的根本原因,将其成为改进软件测评过程的依据。缺陷统计内容包括:

对α向量进行归一化处理,即可得到导弹可用度矩阵A。
4 典型导弹装备使用可用度评估验证
4.1 数据统计分析
以部队现役具有代表性的反舰导弹作为研究对象,选取三个典型储存地域进行调研,根据调研数据时间统计实际情况,由于时间难以精确到时、分,将时间单位以天计,不足一天按一天计算,考虑到每个单位导弹批次和服役年限各不相同,在此以服役年限为单位,所有导弹统计时间的平均值作为使用可用度计算参数指标。维修导弹数量包括故障维修导弹和预防性维修导弹数量。不能工作总时间是根据维修时间的起点和修竣部队验收这个时间段来统计。修复性维修引起的不能工作时间是从测试或发现故障时刻算起,直至修竣验收合格、部队接收;预防性维修引起的不能工作时间是从送修时刻开始至修竣验收合格时刻、部队接收。维修总时间是实际用于导弹预防性维修和修复性维修的时间。
根据调研所得的维修导弹统计数据,由式(2)可得各单位导弹的使用可用度情况如表1所示,根据统计数据,得到该型导弹使用可用度与服役年限的关系如图2所示。

表1 导弹使用可用度统计情况

图3 海军导弹使用可用度变化趋势图
根据图3可以看出,导弹战备完好率变化趋势。在服役1~4年内均能保持较高水平;服役年限5~6年,导弹在温、湿、振动等综合环境应力影响下,质量状态变差,完好率降低;在经过5~7年期间的大中修之后,服役8~9年的导弹完好率增加。
根据图3可以看出,导弹使用可用度的变化趋势,在服役1~4年内均能保持较高水平;服役年限5~6年,导弹在温、湿、振动等综合环境应力影响下,质量状态变差,同时由于故障增多和预防性维修活动,导弹使用可用度明显降低(其中,有个别年份完好性已低于90%,亟需进行预防性维修);在经过5~7年期间的大中修之后,服役8~9年的使用可用度增加。
4.2 使用可用度评估验证
根据对调研数据分析,自动驾驶仪、雷达、火工品以及电气四个分系统故障率相对较高,因此计算导弹使用可用度主要考虑它们的影响。根据统计数据计算得到各分系统MTBF和MTTR如表2所示。

表2 统计数据表
假设各分系统在启用前的状态集{新,堪,待,废}对应模糊矩阵为

设μ1、μ2、μ3、μ4分别取0.8、0.6、0.4、0.2,则:
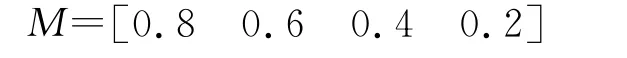
设火工品和电气可用度分别为A1、A2,则有:

经计算求得:

设每枚导弹驾驶仪和雷达的可用度分别A3q、A4q,则有:

经计算可得:

首先考虑每枚导弹由其驾驶仪和雷达组成的小串联系统Ac的可用度分布为

当j=2,3,4时,有:

由此可得四个小串联系统的可用度分别为

为了评估导弹装备整体可用度水平,可把这些小串联系统视为高一级的大串联系统,可用度AD表示:

利用下列公式可求出AD值:
经计算可得:

火工品、电气和上述系统构成整个评估目标,它们之间是串联关系,所以可得整体可用度A0为

从A0可判断出,该单位此型导弹目前处于“新”的概率为0.0429,处于“堪用”状态的概率为0.8995,处于“待修”的概率为0.0576,与统计数据较为吻合,总的来看,导弹可用状态较好,能够满足作战需要。
此种方法仅需要知道各系统MTBF和MTTR、各系统之间结构组成关系以及各系统启用前的状态概率,而且这两个参数可通过记录日常故障数据计算得到,状态概率也可根据质量监控等级来统计计算,为计算导弹可用度提供了便利,克服了根据可用度计算公式需要统计各种时间(这些时间目前记录不完备)的繁琐过程。
通过上述计算,不难得出以下几点结论:
1)在计算可用度时,MTBF、MTTR取值要根据最近所统计的时间进行求解,以使之符合系统的最新状况,为此,在日常工作中,相关单位要做好有关导弹装备工作时间、修理时间统计工作,为分析导弹可用度提供必要的基础数据。
2)导弹装备的可用度只能大体说明导弹装备目前的状态和质量水平,在使用前还需对导弹进行专门的测试和检查。
3)导弹可用性分析在部队的装备管理中应作为一项经常性工作,使之可以对导弹装备运行状况起到监测作用,以便可以实时掌握导弹装备所处的状态。
4)通过导弹可用度的分析,可为导弹维修提供依据。例如当导弹可用度中“堪用”的概率较高时,说明导弹应进行一般性修理;当“待修”的概率较高时,说明导弹需要进行彻底的修理。
5 结语
本文对影响导弹装备战备完好性的重要参数使用可用度参数进行了研究,给出了使用可用度参数的表述,构建了基于可用性理论的导弹装备使用可用度评估模型,并结合实际导弹装备服役信息的相关统计信息,有效地对该模型进行了评估验证,证明了该方法对评估导弹装备使用可用度的效果,并结合评估结果给出了部队导弹装备保障工作中的几点建议,为后续如何提出改进导弹装备战备完好性提供了借鉴。
[1]李院生,时和平.装备战备完好性及其影响因素分析[J].电子产品可靠性与环境试验,2007,25(1):38-41.
[2]花兴来,刘庆华.装备管理工程[M].北京:国防工业出版社,2002:12-15.
[3]施建荣.舰船系统战备完好性的确定和评估步骤[J].电子产品可靠性与环境试验,2004,16(5):1-4.
[4]李刚,陈国通,蔡金燕,等.电子装备战备完好性预测模型研究[J].现代电子技术,2002,27(8):62-64.
[5]刘冰,朱小东,王小魏.装备战备完好性的模型预测研究[J].兵工自动化,2005,24(3):8-9.
[6]程文鑫,陈立强,龚沈光,等.基于蒙特卡洛法的舰船装备完好性仿真[J].兵工学报,2006,27(6):1090-1094.
[7]魏勇,徐廷学.基于任务的舰炮装备战备完好性建模与仿真研究[J].火炮发射与控制学报,2010,25(12):15-18.
[8]杨继坤,徐廷学,闫群章,等.导弹武器系统完好性仿真模型研究[J].舰船电子工程,2009,29(7):168-172.
[9]毛炳祥,白桦,程文鑫.系统战备完好性分析、计算与检测[M].北京:国防工业出版社,2012:3-5.
[10]彭立影,甘传付,熊菊水.地空导弹装备战备完好性指标确定方法研究[J].弹箭与制导学报,2010,30(6):63-65.

