基于道格拉斯改进的雷达回波数据简化算法
熊 欣, 张新宇, 王金涛
(大连海事大学 航海动态仿真和控制交通行业重点实验室, 辽宁 大连 116026)
基于道格拉斯改进的雷达回波数据简化算法
熊 欣, 张新宇, 王金涛
(大连海事大学 航海动态仿真和控制交通行业重点实验室, 辽宁 大连 116026)
为提高雷达模拟器生成物标回波的效率,提出一种基于道格拉斯改进的雷达回波数据简化算法。首先,提取电子海图岸线数据,分析人工岸线和自然岸线的特征;其次,对数据进行预处理,去除冗余点;随后,通过提取岸线数据特征点,将岸线按特征点分段;最后,基于改进的道格拉斯算法,设置压缩比自适应控制各分段的简化阈值,实现各分段数据的简化。经实验验证,该方法能够有效保持岸线地貌特征,并可达到简化的效果。
船舶工程;雷达数据简化;道格拉斯改进算法;自适应阈值;特征点提取;分段简化
目前,雷达模拟器使用的模拟雷达数据一般由电子海图数据直接生成,其回波仿真效率较低。若雷达模拟器直接根据该数据生成回波,当仿真大范围回波时,需要多组雷达模拟数据,尤其是在雷达数据较为复杂时,将耗费计算机大量内存,不能满足实时生成回波的要求。因此,对于模拟器实时生成回波而言,简化雷达回波数据具有重要的现实意义。
关于雷达回波数据简化的研究目前还比较少。在地理综合制图方面,有关线要素简化的研究[1-5]较多,具有一定的参考意义,其中D-P算法(道格拉斯算法)作为一种经典的全局化简方法被广泛运用。该算法基于ATTNEAVE[6]的理论,曲线图形的信息主要集中在曲线的特征点(大多集中于弯曲较大的地方[7])上,通过递归的方法筛选曲线上的点。D-P算法是最具代表性的空间图形的综合方法,不仅可以实现图形特征的分解与组合,而且能够保留图形的方向、尺度、形状等形态和拓扑特征。基于D-P算法的特性,刘欢等[8]提出一种基于D-P算法并结合“扩陆缩海”的思想,通过分维估值的方法实现岸线的自动综合;陈惠荣等[9-10]提出以曲线骨架线作为化简指标的综合方法提取岸线的重要骨架,可同时优化海岸线的自动综合;毋河海[11]通过以双侧偏移量和等值偏移值为指标的曲线综合方法,进一步提升了曲线简化后的精度;XIE等[12]提出基于D-P算法,通过改进公差和曲率的范围保持岸型;LI等[13]提出以角点检测的方法改进D-P算法,实现简化的快速逼近。
海图中的人工岸线(码头、防波堤等)虽然地貌特征明显、数据量少,但对船舶(尤其是进出港口作业的船舶)的航行安全意义重大,因此需精确保留原始形态特征,几乎不用简化。自然岸线地貌特征复杂、数据量大,由于船舶均远离该岸线航行,对航行安全无较大影响,因此可大幅度简化其数据。
由上可知,需将人工岸线和自然岸线分开处理。目前,对于雷达回波的简化仍没有成熟的算法。本文针对电子海图岸线数据的特性,提出一种基于D-P改进的算法,以简化雷达回波数据,进而提高模拟器生成岸线及物标回波的效率。
1 基于D-P改进的雷达回波数据简化算法
1.1雷达回波数据特征分析
雷达回波数据具有如下特点:
1) 数据量大。海图包含的目标丰富,如岛礁、浅滩、人工建筑等。
2) 数据中存在误差。数据采集中存在误差,如可能出现重合点。
3) 数据特征差异大。人工岸线几何精度低,地貌特征明显;自然岸线几何精度高,无明显地貌特征。
4) 数据分布不规则。人工岸线数据较少,分布无规律;自然岸线数据量大,分布较为均匀。
海图部分岸线特征见图1。
1.2数据预处理
由于雷达回波具有数据量大、存在误差、分布不规则等特点,需对其进行预处理。步骤为:
1) 统计岸线数据各点与之前后两点构成的角度分布情况。
2) 删除在设定容差范围内的数据,有效去除重合点及高密度的数据,进而初步简化。
删除点A容差范围内的重合点高密度点A1、A2,删除B的重合点B1(见图2)。
1.3岸线分段
基于自然岸线与人工岸线的特性,若按传统D-P算法对整条岸线统一简化处理,显然无法全部适应岸线的特征,难免出现失真、自相交等情况。为保持岸线地貌特征,避免自相交等情况出现,提出基于骨架特征点,分段简化数据。
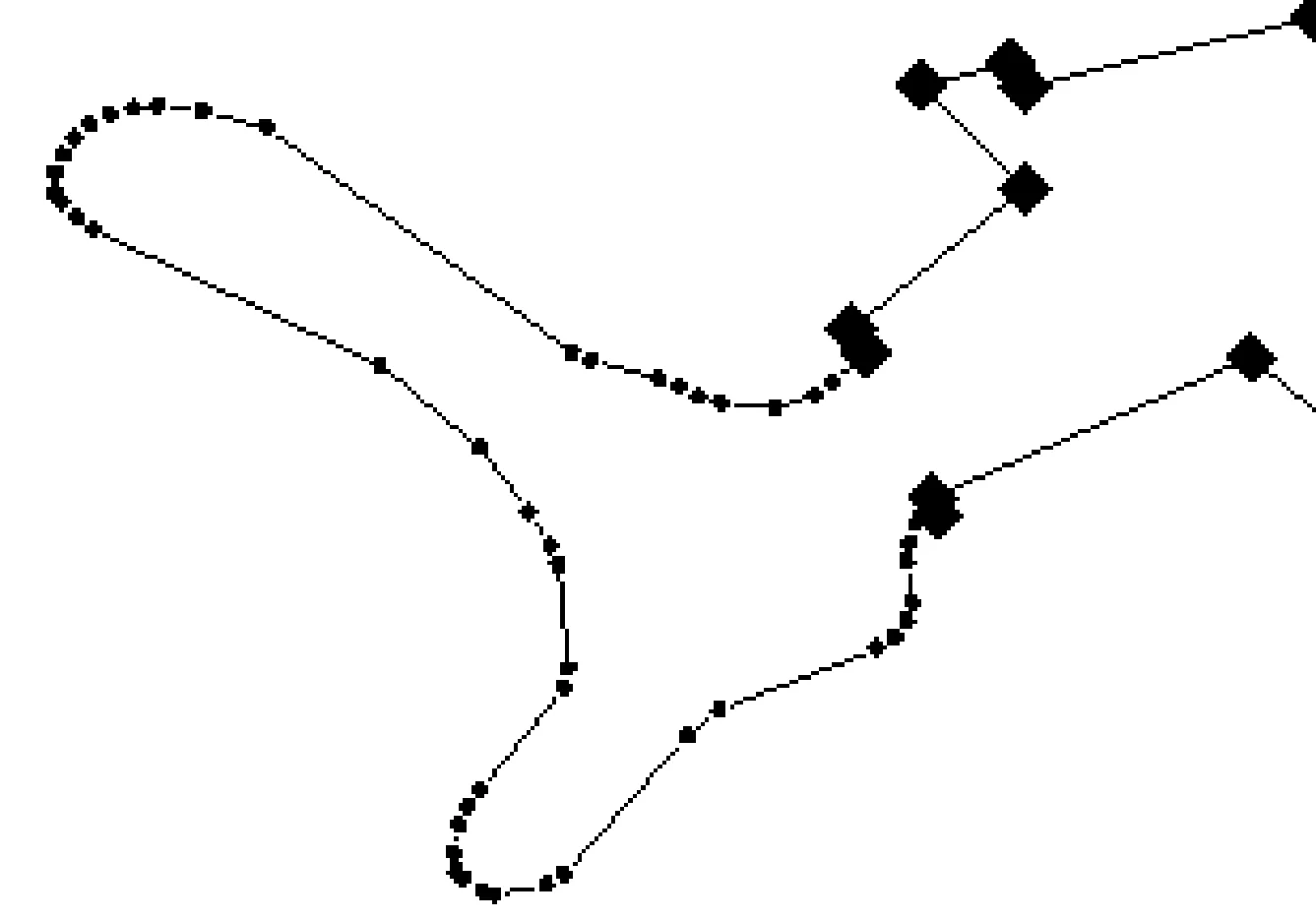
(a) 自然岸线特征
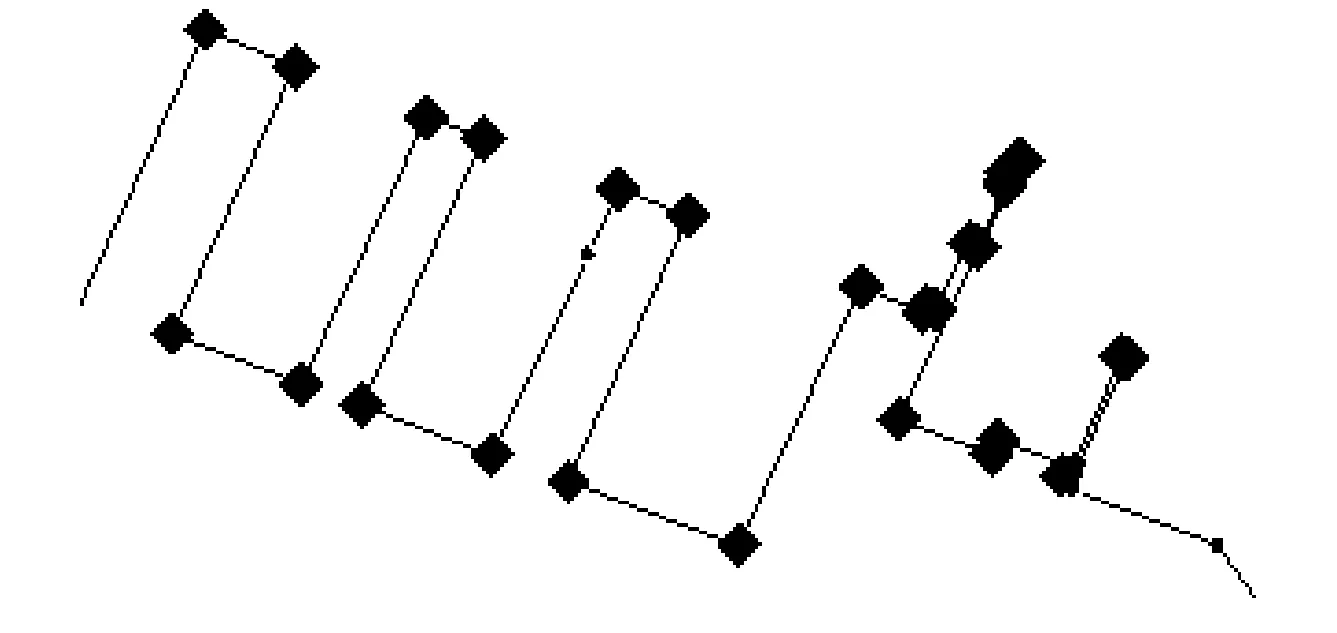
(b) 人工岸线特征
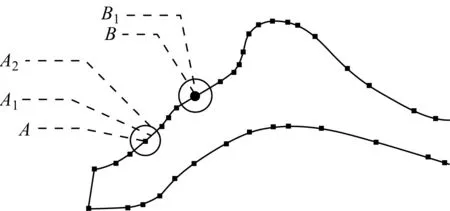
图2 删除冗余点
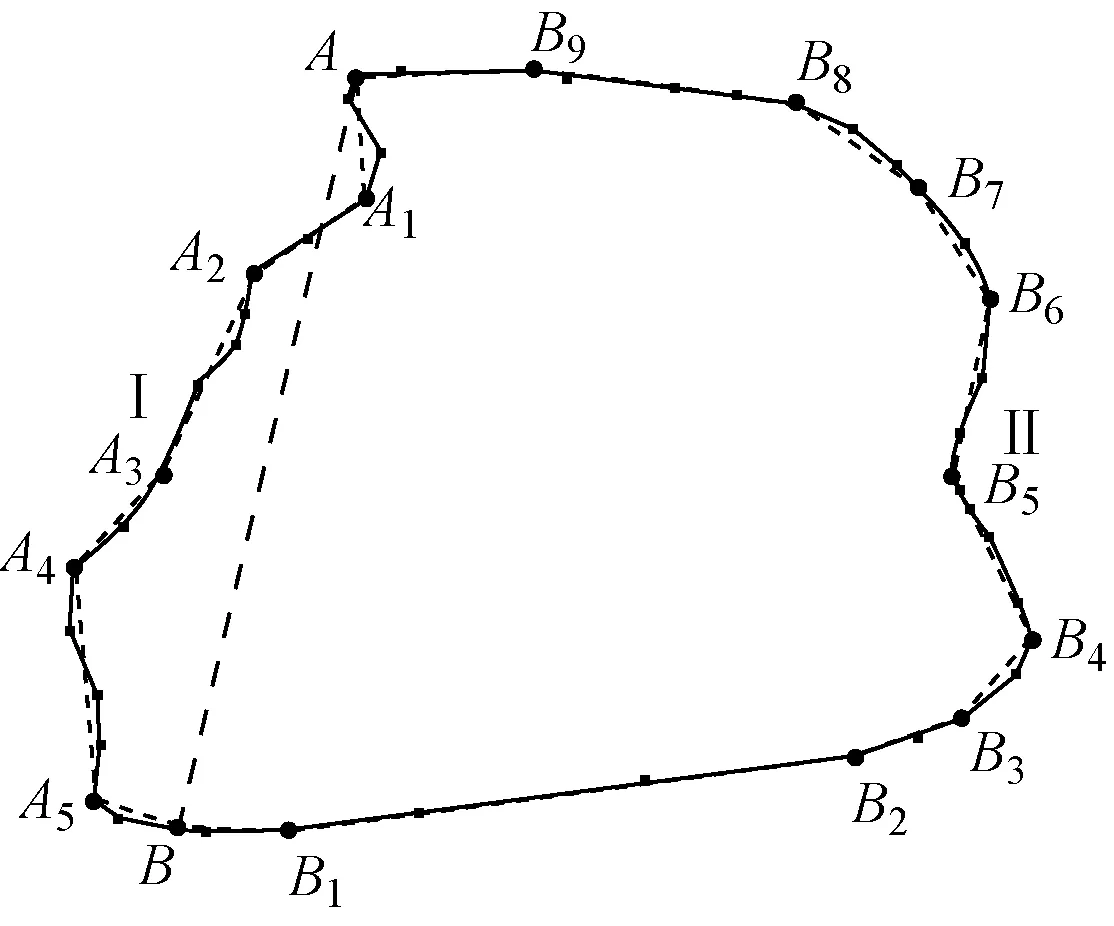
岸线的地貌特征可由特征点保持,通过分析角度分布规律,选取合理角度范围内的点作为特征点对其分段。在海图岸线中,特征点由明显凹凸点、尖角点、码头等局部极值点构成。岸线分段如图1所示,其中小圆点为原数据点,大菱形为特征点。
1.4数据简化
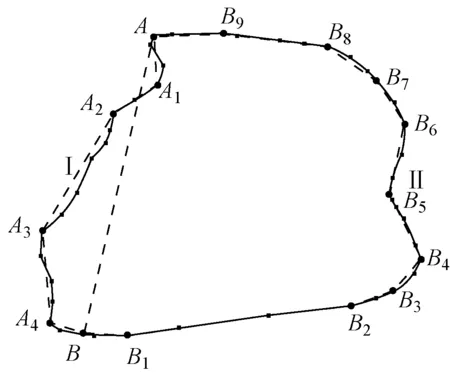
传统的D-P算法通过设定阈值对数据进行统一简化,若数据特征差异较大,则不能合理简化。分段点A,B将曲线分为Ⅰ,Ⅱ两部分,且差异较大。若对岸线Ⅰ,Ⅱ设定统一阈值20,保留的点为A,A1,…,A4,B,B1,…,B9,简化效果见图3(a)。若对岸线Ⅰ设定阈值10,对岸线Ⅱ设定阈值20,保留的点为A,A1,…,A5,B,B1,…,B9,简化效果见图3(b)。简化结果验证,对岸线分段设定阈值的简化效果优于统一设定阈值的简化效果。分段设定阈值简化后的点生成的曲线与原始岸线具有更高的拟合度。
因此,在各分段岸线中,需分别设定阈值进行数据简化处理。但对于数据量大的海图,分段较多且特征不一,若通过人工设定各分段阈值,计算量大,算法复杂且不科学。
提出基于D-P的算法,通过设定压缩比自适应寻找合理阈值,进而简化各分段数据。具体步骤为:
(a)
(b)
1) 设定压缩比,确定各分段岸线简化后保留的数据点的数量。根据该算法,压缩比与简化点数存在关系式
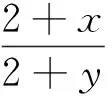
(1)
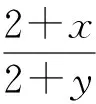
例如,某段岸线中含28个数据点(不含两端点),设定压缩比为0.3,则简化后保留9个点(包括两端点)。若某段岸线中含4个点,设定压缩比为0.3,则简化后保留2个点(包括两端点)。
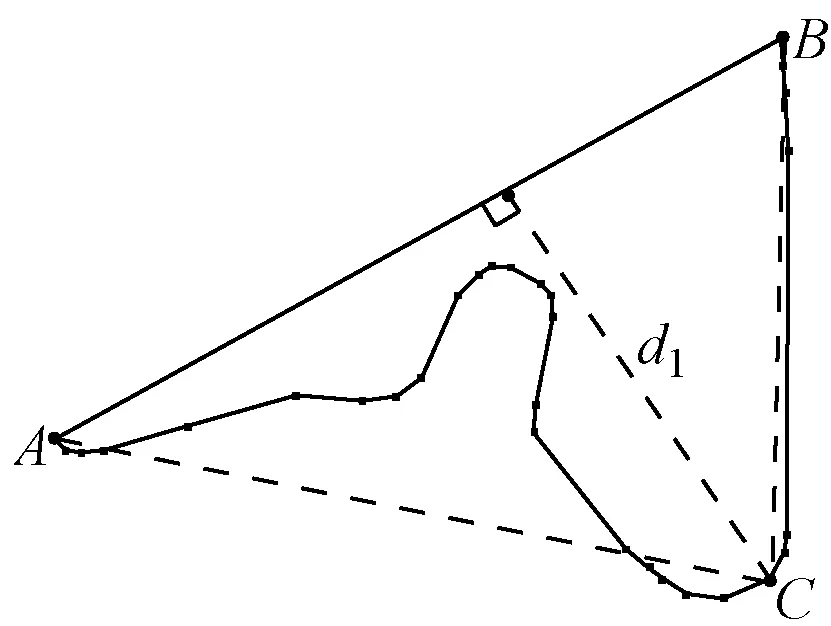
2) 计算初始阈值。初始阈值即遍历曲线间各点到分段点连线的距离中的最大值。图4(a)中,C到A,B连线的距离d1最大,以此作为初始阈值(d1)。通过D-P算法简化,保留C点,则C为新的分段点。
3) 适应寻找阈值。初始阈值按既定步长逐步减小,当其小于/等于遍历曲线间各点到新的分段点连线的最大值时,以此为新的阈值进行D-P简化。图4(b)中,阈值d1按步长逐步减小,当其≤d2时,保留新的分段点D,其中d2分别为AC,CB间各点到AC,CB连线的最大距离。此时以d2为新的初始阈值,D为新的分段点。
4) 重复步骤3),直到满足步骤1)确定的简化结果。图4(c)中,C,D,…,I为依次简化保留的点。
(a)
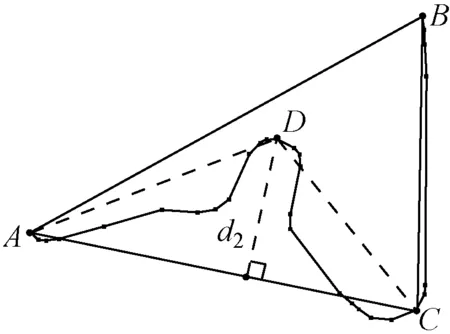
(b)
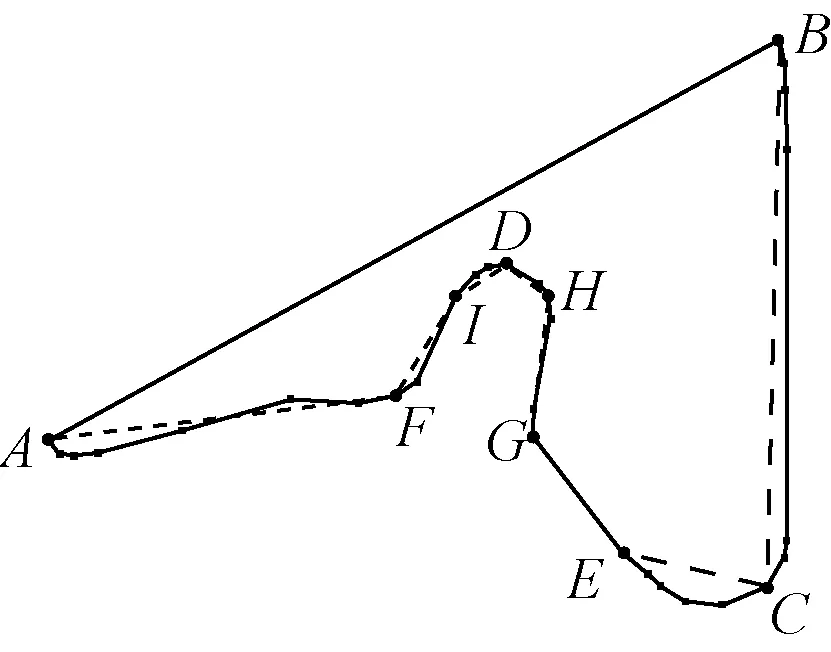
(c)
2 算法设计及实例分析
2.1D-P改进算法
D-P改进算法的流程见图5。
1) 读取电子海图岸线数据。
2) 对数据进行预处理,去除冗余点。
3) 提取特征点将岸线分段。
4) 基于改进的D-P算法,设置压缩比自适应控制各分段的简化阈值,实现各分段的数据简化。
2.2案例分析
以C1511381中大连港电子海图数据为例,利用D-P改进的简化算法对电子海图的数据进行简化,通过对比简化前后的图形说明该算法的可行性。具体步骤为:
1) 数据预处理。原大连港电子海图数据为3 252个点,初步简化后为3 077个点。
2) 特征点分段。大连港包含人工岸线、自然岸线,其中:人工岸线数据点与之前后点构成的角度大多分布在90°~110°;自然岸线数据仍占多数,其数据点与之前后构成的角度大多分布在130°~180°。通过统计各数据点角度分布情况,选择合理的角度提取特征点,进而对岸线进行分段。
3) 数据简化。以图中部分岸线为例。岸线共有25个数据点,若设压缩比为0.3,则应保留8个点。遍历曲线间各点到分段点连线的距离中的最大值,C到AB的距离最大,保留C点及其阈值794。阈值按步长逐步减小并以C点为新的分段点,D到CB间距离为局部最大,保留D点及其阈值299。依次简化,得到C,D,…,H点。简化过程对应阈值及其保留的数据点见表1。简化过程如图4。
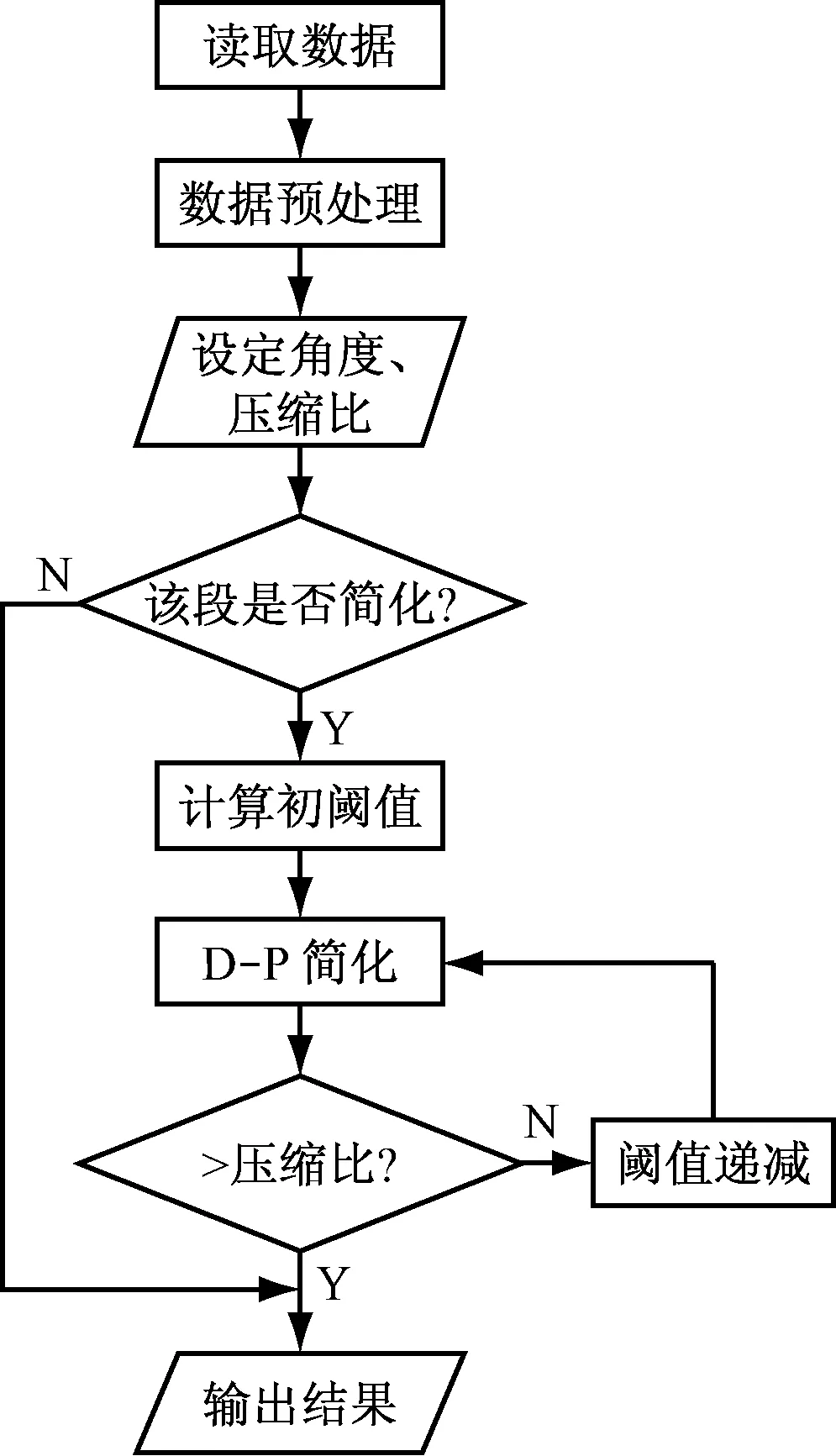
图5 算法流程

表1 简化点及对应的阈值
4) 简化结果对比。大连港局部图若分别设置压缩比为0.3,0.4,0.5,相应的简化效果见图6(a),图6(b),图6(c)。通过简化,可保留岸线特征,设定的压缩比越大,越能更精确地保持岸线特征。
通过设置不同压缩比,可计算出不同的长度误差(即简化前后的长度差与简化前长度的比值),利用相关文献[14]方法证明,长度误差越低则越能替代原岸线。分别设置压缩比0.3,0.4,0.5,自适应寻找阈值进行D-P简化,随着压缩比增大,简化前后的岸线相似度也变高。其长度误差分别为0.004 93,0.002 60,0.001 16。
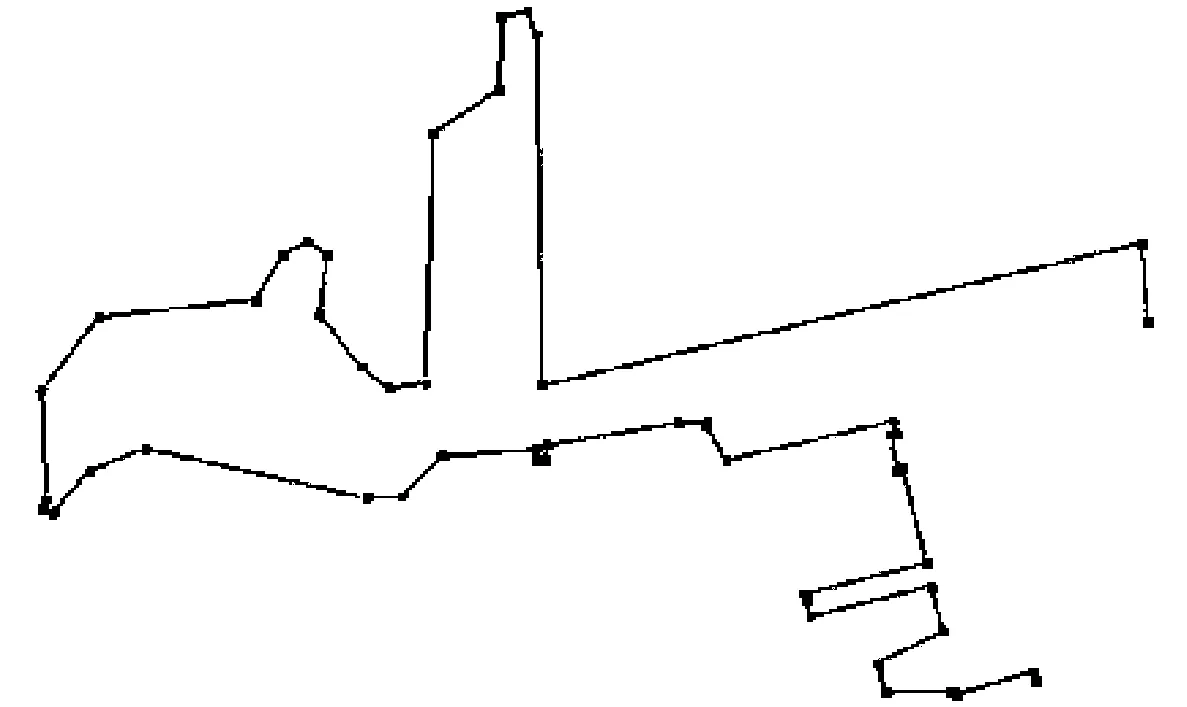
(a)
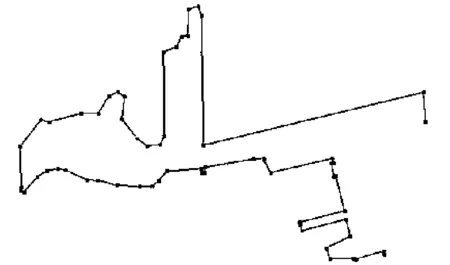
(b)
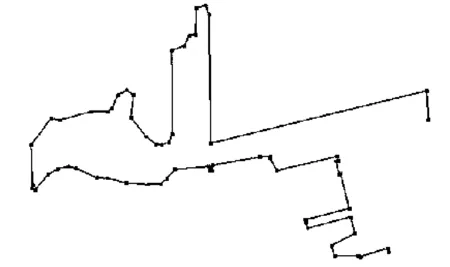
(c)
经实际系统运行验证,利用简化后的雷达模拟数据生成的雷达回波与利用原始数据生成的雷达回波拟合度很高,达到了仿真精度的要求。同时,简化后的雷达模拟数据可大幅度提高雷达回波的显示效率,满足系统实时性的要求。
3 结 语
通过基于D-P改进的算法简化电子海图岸线数据,能够有效保持原有岸线形态特征。对于码头、防波堤等人工岸线,可以保留原始形态;对于自然岸线,既可以保持岸型又可大量简化数据。简化后的岸线数据可以满足雷达回波数据实时生成,设置不同压缩比可以满足对不同精度的需求。若以更加精确的条件进行岸线分段,可以进一步提高其简化效果。因此,运用基于D-P改进的简化算法简化电子海图数据,对于提高航海模拟器实时显示物标回波、保障航行安全而言具有重要意义。
[1] 刘鹏程,罗静,艾廷华,等.基于线要素综合的形状相似性评价模型[J].武汉大学学报:信息科学版,2012,37(1):114-117.
[2] 朱鲲鹏,武芳.线要素化简算法的传递误差模型[J].武汉大学学报:信息科学版,2007,32(10):932-935.
[3] 陈波,朱鲲鹏,薛本新.线状要素化简算法的分析与评估[J].测绘科学技术学报,2007,24(2):121-124.
[4] 王玉海,朱长青,游雄,等.基于B样条小波的等高线数据简化[J].测绘科学,2003,28(2):23-25.
[5] 曲均浩,程久龙,崔先国.垂直剖面法自动提取山脊线和山谷线[J].测绘科学,2007,32(5):30-32.
[6] ATTNEAVE F. Some Informational Aspects of Visual Perception[J]. Psychological Review, 1954, 61: 183-193.
[7] KELLEY P S. Information and Generalization in Cartographic Communication[D]. Seattle: University of Washington, 1977.
[8] 刘欢,谢三德,王芳.海岸线自动综合方法综述[J].测绘科学技术学报,2010,27(3):225-228.
[9] 陈惠荣,彭认灿,郑义东,等.以弯曲骨架线为化简指标的海岸线综合方法[J].武汉大学学报:信息科学版,2011,36(12):1 418-1 422.
[10] 陈惠荣,郑义东,关海波,等.基于骨架线的Douglas-Peucker算法改进[J].海洋测绘,2011,31(5):18-20.
[11] 毋河海.基于多叉树结构的曲线综合算法[J].武汉大学学报:信息科学版,2004,29(6):479-483.
[12] XIE Zhong,WANG Huimin,WU Liang. The Improved Douglas-Peucker Algorithm Based on the Contour Character[C]. The 19th International Conference on Geoinformatics, 2011.
[13] LI Lelin,JIANG Wanshou. An Improved Douglas-Peucker Algorithm for Fast Curve Approximation[C]. 3rd International Congress on Image and Signal Processing, 2010.
[14] 武芳,朱鲲鹏.线要素化简几何精度评估[J]. 武汉大学学报:信息科学版,2008,33(6):599-603.
SimplifyingRadarEchoSimulationwithImprovedDouglas-PeuckerAlgorithm
XIONGXin,ZHANGXinyu,WANGJintao
(Marine Dynamic Simulation and Control Laboratory, Dalian Maritime University, Dalian 116026, China)
An improved Douglas-Peucker algorithm is proposed to reduce the amount of work to paint the radar echo of shorelines on simulator screens. The shoreline data are extracted from electronic charts. The data are preprocessed to distinguish artificial from natural shorelines according to their characteristics and to remove redundant points. The processed shoreline is segmented according to the feature points. The shoreline data are finally processed according to set compression ratio by an Douglas-Peucker algorithm with segment adaptive threshold control to form an compressed shoreline data set. Experimental results show that the proposed method can effectively reduce the volume of data while keeping the shape of shorelines satisfactorily.
ship engineering; radar data compression; improved Douglas-Peucker algorithm; adaptive threshold; feature point extraction; sectional approximation
2014-05-18
国家自然科学基金(51309043);交通运输部基础应用研究项目(2014329225020);中国博士后科学基金(2014M551095);辽宁自然科学基金(2014025005);中央高校基础研究基金(3132014202)
熊 欣(1988—),四川遂宁人,男,硕士生,研究方向为交通信息工程及控制。E-mail:dmu_2012xx@163.com
张新宇(1978—),吉林长春人,男,博士生,研究方向为交通信息工程、航海动态仿真、电子海图系统等。
E-mail:zhang.xinyu@soho.com
1000-4653(2014)03-0001-04
TN957.51
A

