扫描镜稳定度对TDI CCD测量精度的影响
贺小军 ,曲宏松,张贵祥,王金玲
(1.中国科学院长春光学精密机械与物理研究所,吉林长春130033;2.小卫星技术国家地方联合工程研究中心,吉林长春130033)
1 引言
按传感器类型角度分类,光学测量系统可分为面阵传感器光学测量系统和线阵传感器光学测量系统,其中面阵传感器光学测量系统以星敏感器为代表,它不含扫描机构,直接将目标置于光学视场内,测量其空间角位置信息,得到目标相对于光轴的角位置偏差。这种系统由于受到视场角及光学分辨率的影响,测量的角度范围较小,测量精度较低,但由于不需要高精度的扫描机构,实现难度较低,所以广泛应用于星敏感器、飞船的交汇对接等领域。线阵传感器光学测量系统采用线阵传感器,需要借助扫描机构实现扫描成像,可实现大范围的目标搜索,利用长线阵传感器可以实现高精度的测量,这类系统广泛应用于预警、目标搜索等领域,其中采用时间延迟积分电荷耦合器件(TDI CCD)作为传感器的光学测量系统比普通线阵传感器光学测量系统具有更好的响应特性,能够对暗弱目标进行更为准确的测量,且可与大F数光学系统配合使用,形成重量轻、体积小、测量精度高的光学测量系统。
近年来国内外关于TDI CCD特殊用法研究方面的文章发表较多,薛旭成等人提出了应用双排TDI CCD来提高相机动态范围[1];杨秀彬等人研究了偏流角误差对成像的影响[2];张毅等人研究了亚像元相机的调制传递函数(MTF)特性[3]。
近几年在光学测量方面也有大量研究成果,李喆提出了一种基于光学测量的屏幕光斑的数学模型,用于测量飞行器三维姿态参数[4];齐荔荔等人提出了图像式光电编码器的测角技术[5],薛旭成等人利用TDI CCD相机的图像确定卫星姿态稳定度[6]。
在TDI CCD硬件系统设计及特性分析方面,李豫东、宁永慧、郑亮亮等人在发表的相关文章中进行了详细分析[7-11]。
线阵CCD光学测量系统相对面阵CCD光学测量系统在测量范围、测量精度上都有很大优势。随着高精度扫描机构技术的突破,其在航天领域的应用逐渐增多,尤其是在航天预警、非合作目标搜索等领域。TDI CCD相对传统线阵CCD具有响应度高的特点,可以采用大F数光学系统,从而大大降低系统的体积和质量,使其更加适用于航天应用,所以近年来TDI CCD传感器的光学测量系统逐渐替代了传统线阵CCD的光学测量系统。
但是TDI CCD对像移补偿精度要求较高,所以对扫描镜的研制提出了更高的要求。本文主要采用数值仿真方法研究扫描镜的速度稳定度对测量精度的影响。
2 原理
2.1 目标随机分布与感光面数值模型
由于传感器的像元尺寸不为无穷小,当目标的理想像覆盖在像元不同位置时,其测量误差存在差异。为了模拟真实情况下的测量情况,将目标在像面上的位置用二维随机均匀分布来表示,使得计算结果可信度更高。
根据TDI CCD传感器特点,建立TDI模式CCD的感光面数学模型:
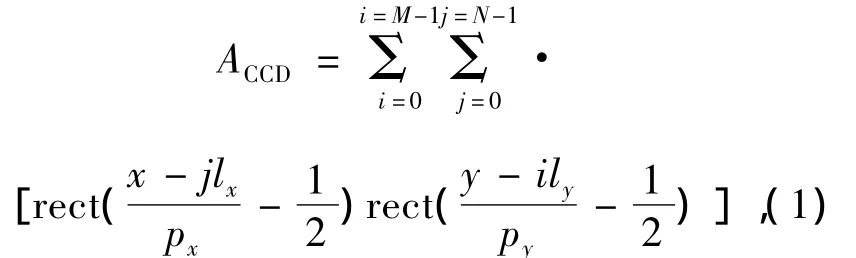
式中,rect(x)为门函数,当|x|≤0.5时,函数值为1,其余为0;lx为X方向像元中心距(μm);ly为Y方向像元中心距(μm);j为传感器像元列序号;i为传感器像元行序号;px为X方向光敏尺寸(μm);py为Y方向光敏尺寸(μm);M为CCD积分级数;N为CCD像元列数。图1为像元感光面结构示意图,其中黑色区域代表不感光区,当填充因子接近100%,图中线条仅代表像素界限。
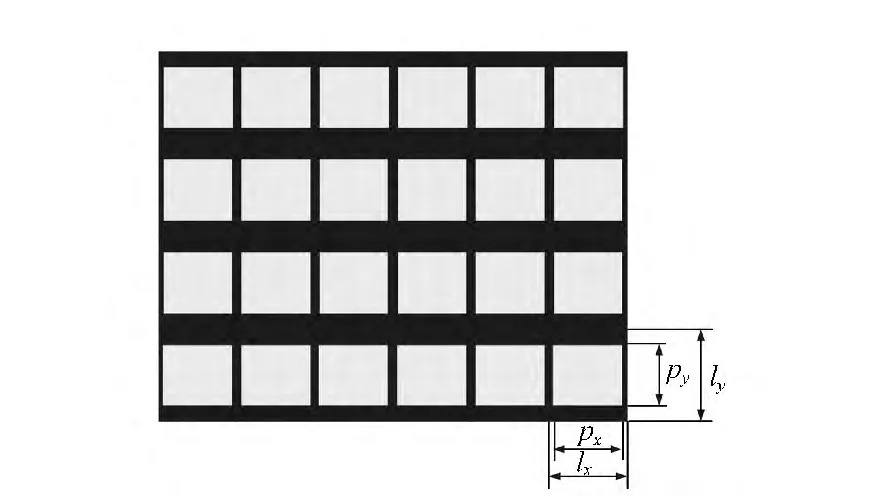
图1 CCD像元结构Fig.1 Structure of CCD sensor pixel
2.2 TDI CCD成像过程数值模型
TDI CCD成像过程分为以下几个主要部分:传感器模拟、光学像模拟、成像过程模拟以及图像处理过程,其功能框图如图2所示,各个部分的主要功能如下。
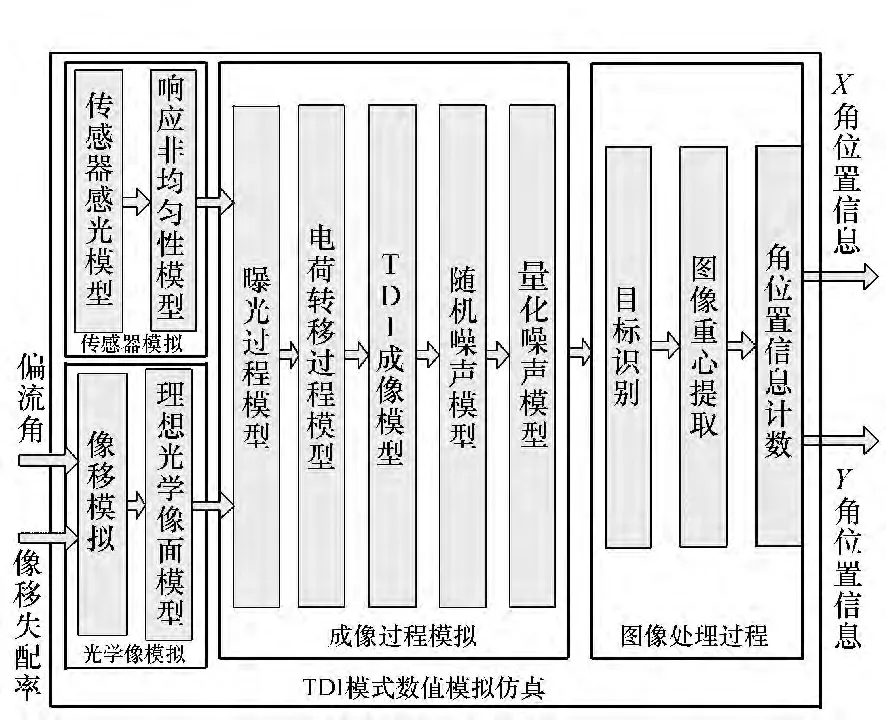
图2 TDI模式评价方案框图Fig.2 Evaluation scheme of TDI mode
(1)传感器模拟:模拟传感器的像元尺寸、填充因子、像元排布方式等特性以及传感器各个像元光电响应的非均匀性。
(2)光学像模拟:将像移矢量引入理想像面,模拟产生实际光学像及像移方式。
(3)成像过程模拟:曝光过程模型采用数值细分的方法,模拟每个像元的光电转化以及电荷积累过程;电荷转移过程模型实现电荷的行间转移与像移速度匹配的数值模拟;图像信号输出模型模拟电荷读出转换为电压信号的过程,每个像元区域内的电荷总量对应一个电压值;随机噪声模型模拟传感器的读出、暗电平噪声、散粒噪声等随机噪声源,加性叠加到图像信号内;量化噪声模型模拟图像信号的量化过程,按照最大动态范围的量化原则进行量化,其中存在截断误差。
(4)图像重心提取:通过图像重心算法计算出目标的XY坐标值。
(5)角位置信息计算:根据光学系统的相关参数以及图像重心坐标值,计算目标的角位置信息。
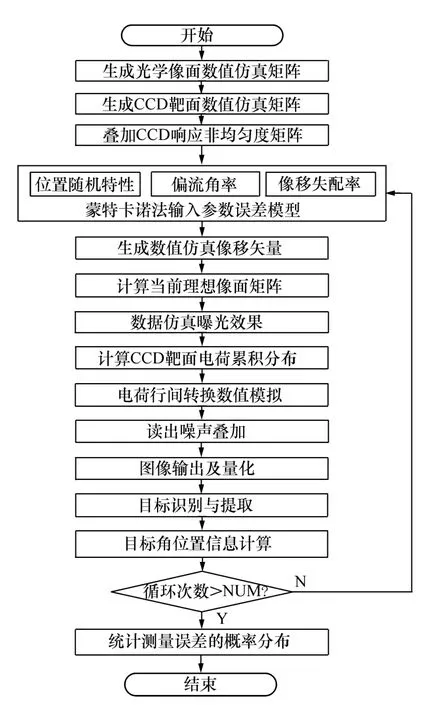
图3 偏流角影响评价软件流程图Fig.3 Software flow of drift angle impact evaluation
本文根据对成像过程的数学化描述,提出了评价算法流程。将某卫星生命周期内的偏流角计算数据代入评价模型,再结合扫描镜速度稳定度等参数,按照蒙特卡诺法进行多次计算,得出在各个参数影响下的测量误差统计曲线。由于误差统计结果基本符合正态分布,根据3σ准则,得到测量误差值,整个评价过程的软件流程图如图3所示。
每次计算过程中,每个随机量均按照自身的随机分布特性,随机选取一个值作为当前取值,经过足够多次数的计算,即可模拟实际情况下各个随机量的真实分布情况,使得获取的统计结果与实际情况的统计结果更加接近,使结果更具有参考价值。
2.3 重心坐标及角位置计算
采用经典的图像重心算法进行计算[4],计算方法见式(2)、式(3):
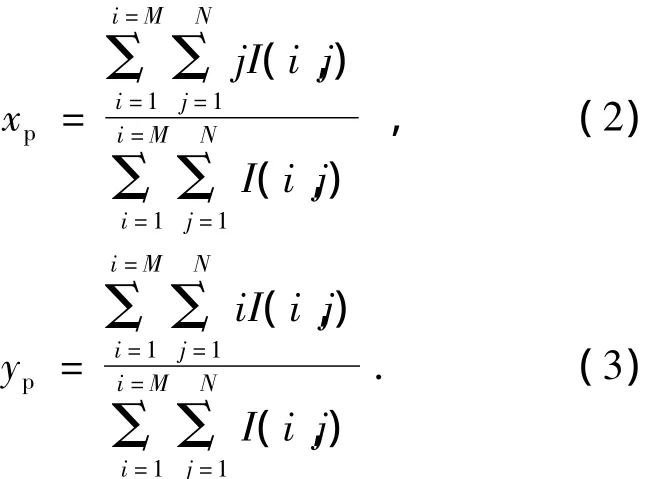
式中:I(i,j)表示第i行j列的图像灰度值,M为图像行数,N为图像列数。
将图像重心坐标代入光学系统的高斯公式[4],将其转换为角位置信息,可以得到目标的方位角β和俯仰角γ:
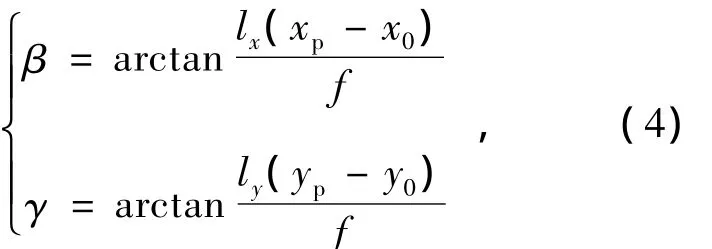
式中:(x0,y0)为相机光轴对应的图像重心坐标;为方位方向的像元角分辨率为俯仰方向的像元角分辨率。本文采用的仿真参数为30 μrad。
3 扫描镜速度稳定度表征
扫描镜在运动过程中,速度会随时间波动,表现为不稳定性[12],通过角位移传感器测定的某工程样机的扫描镜角位移曲线(图4),对其进行差分,得到角速度曲线(图5)、成像期间的角速度曲线(图6)以及角速度的归一化概率分布图(图7)。通过对成像区间的速度精度进行统计,由式(5)得到归一化角速度的标准偏差ε为0.023 8,本文利用速度误差ε来表征扫描镜的稳定度,当速度误差越大,则扫描镜稳定性越差,反之,则扫描镜稳定性越好,当ε为0时,为理想的扫描镜系统,扫描镜为匀速扫描。
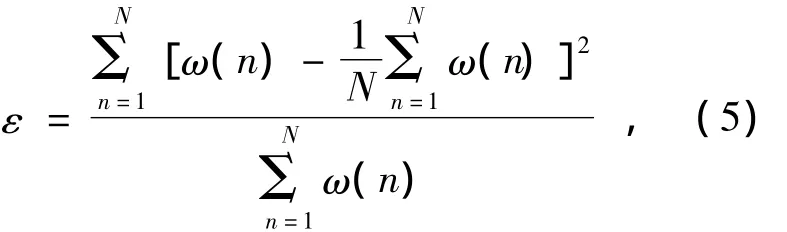
式中,ω为扫描镜角速度,n为采样序号。本文采用正态分布函数来描述扫描镜的速度稳定度。
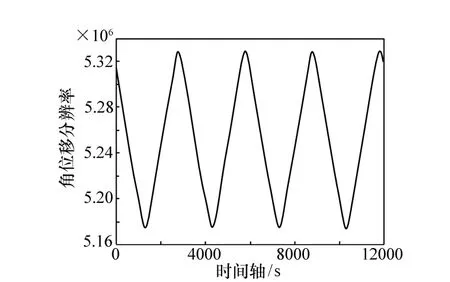
图4 扫描镜角位移曲线Fig.4 Angular displacement curve of scan mirror
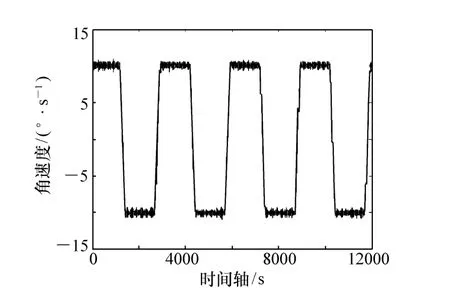
图5 扫描镜角速度曲线Fig.5 Angular speed curve of scan mirror
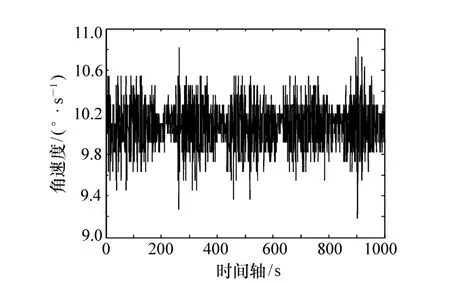
图6 扫描镜角速度曲线(成像段)Fig.6 Angular speed curve of scan mirror(imaging area)

图7 扫描镜角速度标准偏差统计结果(成像段)Fig.7 Standard deviation statistics of scan mirror scan speed(imaging area)
4 数值仿真结果
将扫描镜的速度误差ε带入TDI CCD数值仿真模型,模拟每次扫描成像结果,得到一次测量结果,根据蒙特卡诺法[13-14],对目标位置及其他随机变量进行独立地随机取值,获得大量样本的打靶试验结果,通过对结果进行统计,得到表1所示的统计结果。
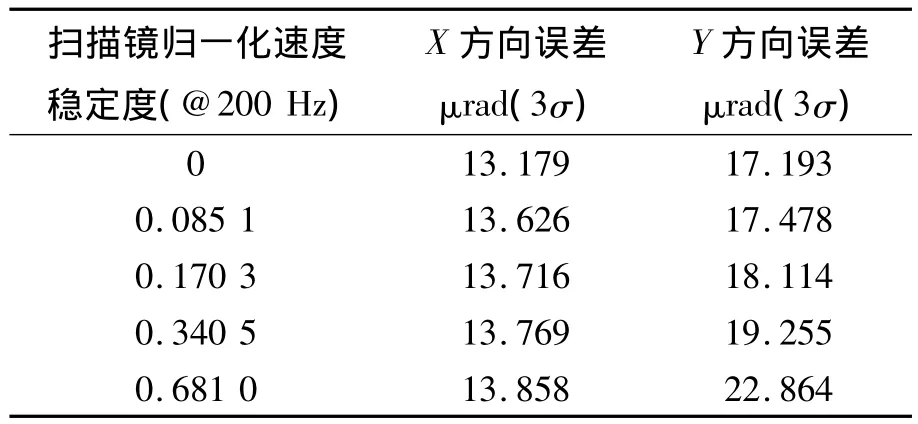
表1 测量误差与扫描镜速度误差统计表Tab.1 Measure error and scan mirror speed error
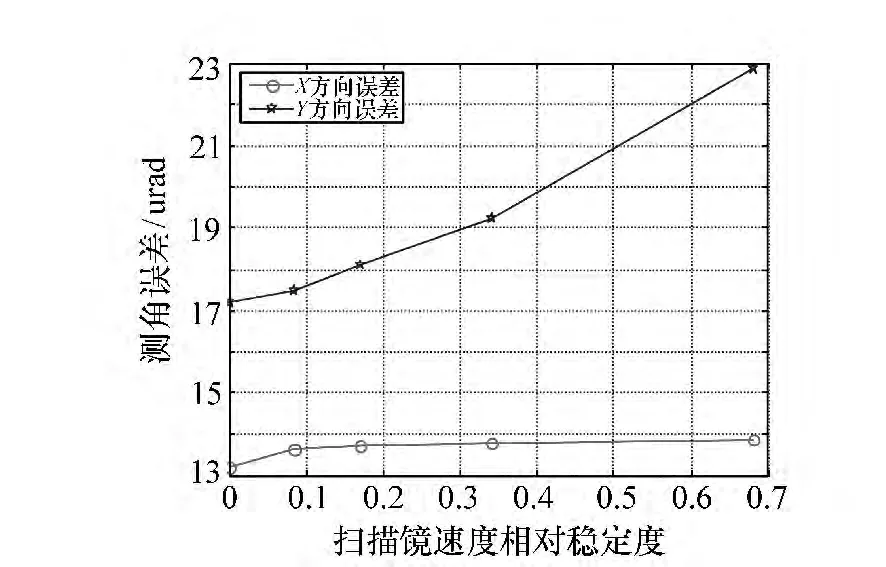
图8 测量误差随扫描镜速度误差的变化曲线Fig.8 Curve of measure error and scan speed error
将某工程样机的扫描镜实测结果代入数值仿真模型,从统计结果可以看出,X方向的测量误差基本不受扫描镜速度误差的影响,Y方向的测量误差随着扫描镜速度误差的增大而增大,基本呈现线性增长,扫描镜速度误差从0变为0.681时,Y向测量误差由 17.193增加为22.864,测角误差增大 5.67 μrad。
5 结论
成像测量系统中,光电成像系统的像元角分辨率和扫描镜的稳定度对测角精度起关键影响,通过对成像测量系统的整个物理过程进行数学建模,得到数值仿真模型,带入扫描镜速度稳定度的实测数据,对扫描镜的测量误差进行估算,实现对系统关键指标的详细论证,可以使得设计最优化,避免对像元角分辨率或扫描镜稳定度提出过高的指标要求。代入某工程样机扫描镜实测数据进行数值分析,结果表明:在200 Hz采样率下,若速度的相对误差为0.681 0,对比速度误差为0的情况,Y方向测角误差增大了近1/3。
[1] 薛旭成,韩诚山,薛栋林,等.应用双排TDICCD提高空间推扫遥感相机动态范围[J].光学 精密工程,2013,20(12):2791-2795.XUE X CH,HAN CH SH,XUE D L,et al..Increasing dynamic range of space push-broom remote sensing camera by tworow TDI CCD[J].Opt.Precision Eng.,2012,20(12):2791-2795.(in Chinese)
[2] 杨秀彬,贺小军,徐开,等.偏流角误差对TDI CCD相机成像的影响与仿真[J].光电工程,2008,35(11):45-50.YANG X B,HE X J,XU K,et al.Effect and simulation of the deviant angle error on TDI CCD cameras image[J].Opto-Electronic Engineering,2008,35(11):45-50.(in Chinese)
[3] 张毅,李英才,王虎.航天TDI-CCD亚像元相机的MTF研究[J].光子学报,2005,34(10):1590-1592.ZHANG Y,LI Y C,WANG H.Analysis of the MTF of the TDI-CCD camera[J].Acta Photonica Sinica,2005,34(10):1590-1592.(in Chinese)
[4] 李喆,丁振良,袁峰.飞行器姿态参数的光学测量方法及其精度的蒙特卡罗模拟[J].吉林大学学报(工学版),2009(39):1401-1406.LI Z,DING ZH L,YUAN F.Optical measurement of aircraft attitude parameters and accuracy Monte Carlo simulation[J].J.Jilin University(Engineering and Technology Edition),2009(39):1401-1406.(in Chinese)
[5] 齐荔荔,万秋华.图像式光电编码器的测角技术及其硬件实现[J].光学学报,2013,33(4):0412001.QI L L,WAN Q H.Angle-Measurement echnology of an optical pattern rotary encoder and its hardware implementation[J].Acta Optica Sinica,2013,33(4):0412001.(in Chinese)
[6] 薛旭成,傅瑶,韩诚山.TDICCD相机的卫星姿态稳定度确定[J].中国光学,2013,6(5):767-772.XUE X CH,FU Y,HAN CH SH.Confirmation of satellite attitude stabilization for TDI CCD camera[J].Chinese J.Optics and Applied Optics,2013,6(5):767-772.(in Chinese)
[7] 李豫东,汪波,郭旗,等.CCD与CMOS图像传感器辐射效应测试系统[J].光学 精密工程,2013,21(11):2778-2784.LI Y D,WANG B,GUO Q,et al..Testing system for radiation effects of CCD and CMOS image sensors[J].Opt.Precision Eng.,2013,21(11):2778-2784.(in Chinese)
[8] 宁永慧,郭永飞.TDICCD拼接相机的像元响应非均匀性校正方法[J].中国光学,2013,6(3):386-394.NING Y H,GUO Y F.Correction of pixel response non-uniformity in TDICCD mosaic camera[J].Chinese Optics,2013,6(3):386-394.(in Chinese)
[9] 郑亮亮,张贵祥,金光.高速多光谱TDI CCD成像电路系统[J].中国光学,2013,6(6):939-945.ZHENG L L,ZHANG G X,JIN G.High-speed imaging circuit system for multispectral TDI CCD[J].Chinese Optics,2013,6(6):939-945.(in Chinese)
[10] 孙景旭,刘则洵,万志,等.CCD成像电子学单元光电参量测试系统[J].应用光学,2013(2):289-294.SUN J X,LIU Z X,WAN ZH,et al.Photoelectric parameters testing system for CCD imaging electronics unit[J].J.Applied Optics,2013,34(2):289-294.(in Chinese)
[11] WONG H S,YAO Y L,SCHLIG E S.TDI charge-coupled devices:design and applications[J].IBM J.Research and Development,1992,36(1):83-106.
[12] CONOVER D M,DELANEY J K,LOEW M H.Accurate accommodation of scan-mirror distortion in the registration of hyperspectral image cubes[J].Proceeding of SPIE Defense,Security,and Sensing on International Society for Optics and Photonics,2013:87431S-87431S-10.
[13] DOUCET A.Sequential Monte Carlo Methods[M].New York:John Wiley & Sons,Inc.,2001.
[14] JACOBONI C,LUGLI P.The Monte Carlo Method for Semiconductor Device Simulation[M].Berlin:Springer,1989.

