自适应光学系统校正后实际分辨率评价指标

卫沛锋，刘欣悦，林旭东，董 磊，王鸣浩

(1.中国科学院长春光学精密机械与物理研究所，吉林长春130033;2.中国科学院大学，北京100049)

1 引言

为了获取空间目标的清晰成像，地基望远镜口径变得越来越大。但随着其口径增大而带来的大气对望远镜分辨能力的限制，使得自适应光学系统成为地基大口径望远镜必不可少的技术单元［1-4］。在实际观测中，由于观测站点的大气视宁度的限制和自适应光学系统自身能力的局限，自适应光学系统对于目标一般只能做到部分校正［5］，达不到衍射极限。空间目标(如卫星、火箭残骸等)多是具有一定空间结构和细节的面目标。为达到空间监视的目的，人们更关心地基大口径望远镜自适应光学系统对空间目标的实际分辨率。因此，选择合适的指标来描述地基大口径望远镜适应光学系统对空间目标的实际分辨率就显得很有必要。

自适应光学系统校正的像差包括望远镜的静态系统像差、装调误差、大气湍流引起的动态像差等。自适应校正后波前探测器测量到的波前特征是实际分辨率评估的主要参考指标。目前常用的评价地基大口径望远镜自适应光学系统实际分辨率的指标有［6-9］斯特列尔比(Strehl Ratio)、半高全宽(FWHM)、点扩散函数(PSF)、光学传递函数(OTF)、波前残差(均方根值:RMS)等。Strehl Ratio、FWHM和PSF比较适合用来评价诸如恒星等点目标［8］的校正性能，对具有结构细节的空间面目标的校正性能评价就显得无能为力。OTF可以全面描述望远镜系统对于目标不同空间频率的分辨能力，但却不是一个综合性指标。RMS的适用性和实用性就相对比较宽泛［9］，但却更倾向于对于畸变波前的实时校正能力的描述，与目标特征无关。另外，Dierickx［10］曾提出一个中央亮度比(Central Intensity Ratio，CIR)的概念，但适合描述点目标。Cagigal［11］提出一个广义Fried参数来描述对目标自适应光学实际分辨率，但在实际工作中，完全良好校正的Zernike多项式项数难于确定，实际应用比较困难。因此，提出一个可以实时反映地基大口径望远镜自适应光学系统对空间目标的实际分辨率的标量指标就显得很有意义。

地基大口径望远镜对空间目标的分辨，通常在自适应校正之后，还通过图像处理等方法［12-13］进一步提高对目标的分辨能力。图像处理对分辨能力的提升不在本文的探讨范围之内。本文仅探讨自适应光学系统直接校正后实际分辨率的评价指标。本文基于望远镜自适应光学校正后的角分辨率和系统参数，提出了一个能够实时描述地基大口径望远镜自适应光学系统对空间目标实际分辨率的指标——可分辨单元数比(RCR)。

2 RCR的理论推导

当地基大口径望远镜自适应光学系统用于空间目标监测时，一般比较关心获取的空间目标的两个特征:目标图像大小和实际分辨率。目标图像大小可用目标在成像相机上所成的像元数、线对或单元数来进行表征。实际分辨率是获取的图像可有效分辨的单元数的比率，这里用可分辨单元数比来表征。

仅考虑几何光学而不考虑大气湍流的影响，理论上目标在成像相机上所成的像元数可用目标对望远镜的张角与成像相机像元尺寸决定的最小角分辨率的比值来表示。目标对望远镜的张角为:

式中，l为目标尺寸，R为目标到望远镜的距离。目标识别中常以两个像素作为一个分辨单元，则成像相机像元尺寸决定的最小角分辨率为:

式中，p为成像相机像元尺寸，f为系统焦距。理论上目标在成像相机上成的单元数为:

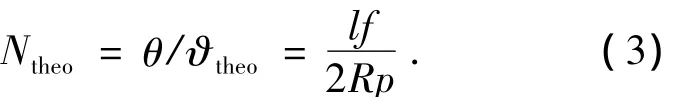
虽然似乎成像的单元数越多越好，但实际这些单元是否包含了我们所关心的目标结构信息，是与望远镜自适应光学系统对空间目标的实际分辨率息息相关。在实际观测中，由于自适应光学系统的部分校正，目标实际可分辨的单元数一般小于目标理论上在成像相机上所成的单元数。因此，自适应光学系统对空间目标的实际分辨率的评价就可以用目标实际可分辨的单元数与其理论上在成像相机所成单元的比值来表示。这个比值被称之为可分辨单元数比。

望远镜自适应光学系统部分校正后达到的角分辨率ϑex可用下式进行估计:

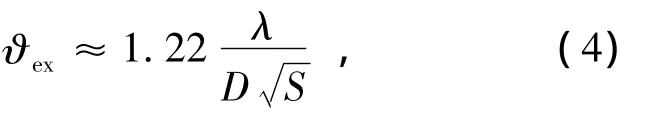
式中，S为校正后的斯特列尔比。

当波前残差σ小于2 rad时，斯特列尔比根据 Marechal近似可表示为［5］:

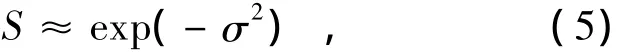
式中，σ为校正后成像相机端的波前残差RMS值，单位为rad。由于实际波前探测器的探测波段与成像相机的成像波段不一致，所以归一化到成像波段等效波长处的波前残差RMS值σ为:

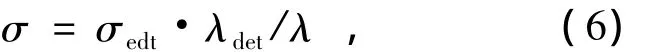
式中，σdet是去除倾斜后的波前探测器等效探测波长下的波前残差RMS值;λdet为波前探测器等效探测波长;λ为成像相机等效波长。将式(6)代入式(5)可得:

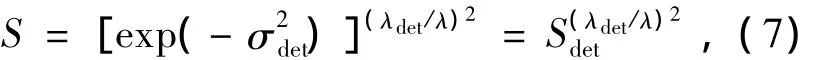
式中，Sdet是波前探测器测量的斯特列尔比。目标实际可分辨的单元数可用目标张角与望远镜的实际角分辨率的比值来表征:

综上可知，可分辨单元数比为:

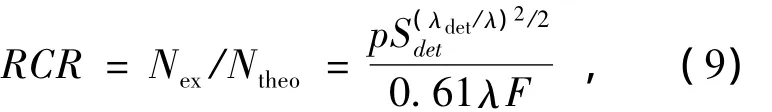
式中，F=f/D。

3 可分辨单元数比的讨论

可分辨单元数比不仅可以描述地基大口径望远镜自适应光学系统对于空间目标的实际分辨率评价，而且它的推论还可拓展到其他方面。下面就可分辨单元数比的物理意义、适用范围、误差分析及大气弥散的影响进行分析。

3.1 可分辨单元数比的物理意义及适用范围

由式(9)可知，可分辨单元数比中不仅包含了实时校正后的斯特列尔比，还包含了望远镜系统参数，如成像相机像元尺寸，系统F数、成像及波前探测波长等。因此，可分辨单元数比可全面实时表征望远镜系统和自适应光学系统的特征。同时，物理意义也极为直观:假设目标理论上在成像相机成10×10分辨单元，50%的RCR就表示实际只有5×5个单元能够有效分辨，其中包含了我们关心的空间结构信息。

因0＜Sdet≤1，故0＜RCR≤1。当0＜RCR＜1时，表示对目标的实际分辨率尚未达到望远镜系统的能力极限;当RCR=1时，表示对目标的实际分辨率达到了系统极限;当RCR＞1时，表示对目标的实际分辨率超过了成像相机像元的空间分辨能力。此时需要对系统的参数进行修改，以避免系统能力的浪费。

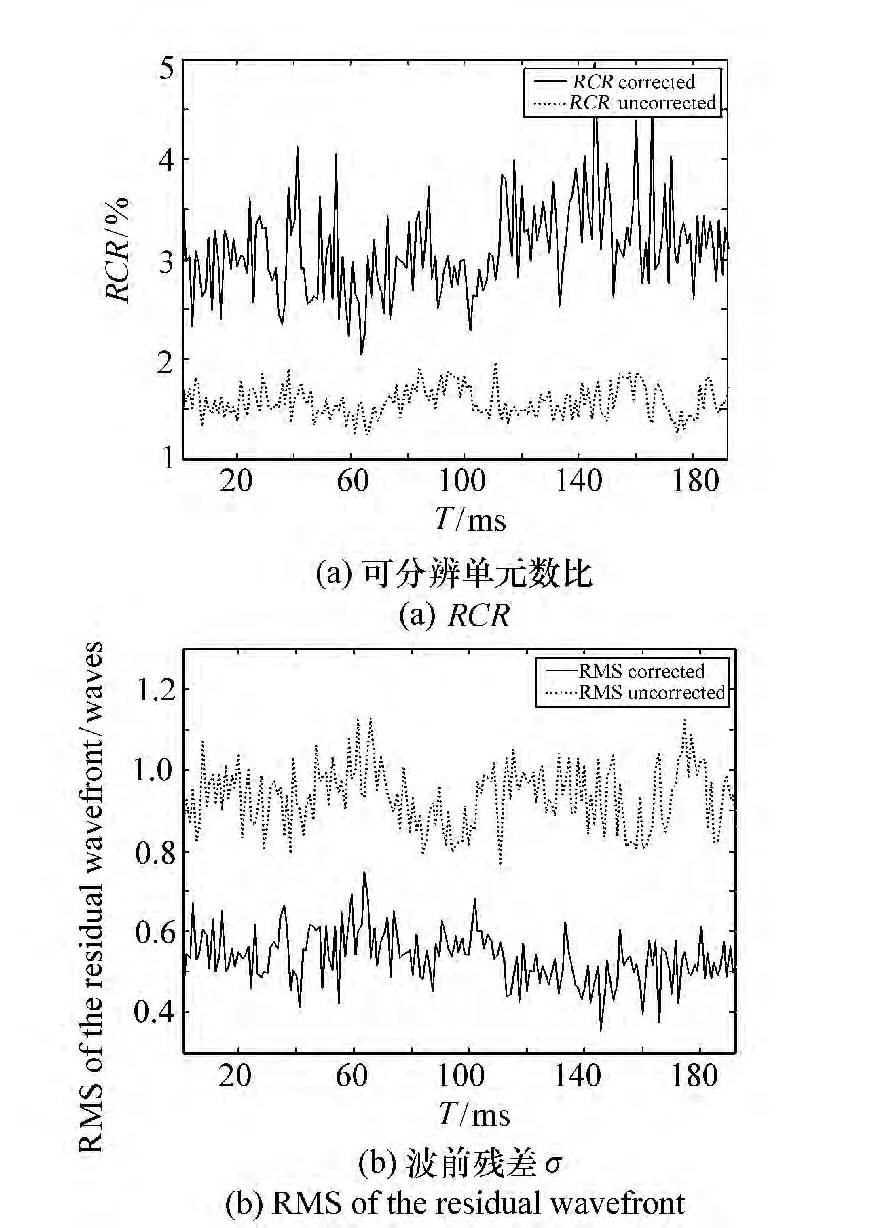
图1 恒星目标校正前后可分辨单元数比与波前残差Fig.1 RCR and the rms of residual wavefront for a fixed star when AO uncorrected and corrected

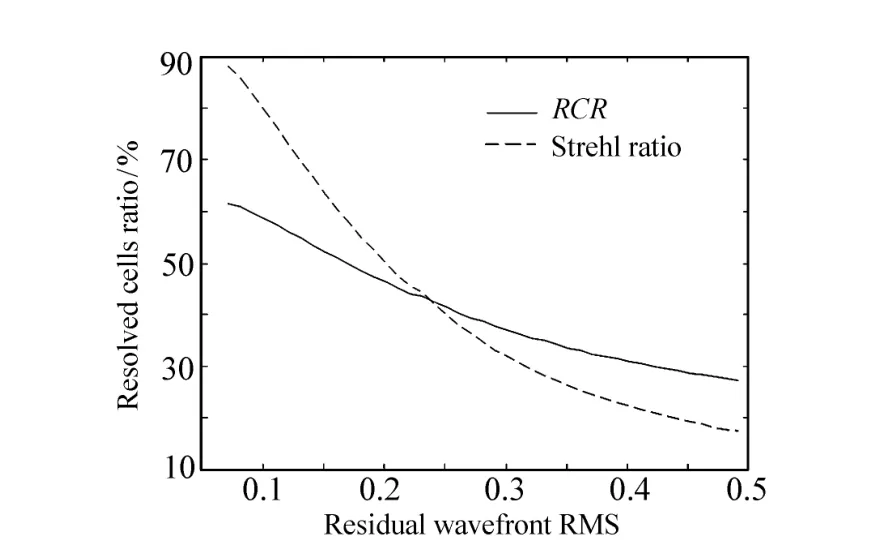
图2 可见光波段可分辨单元数比、斯特列尔比与波前残差σ之间的关系Fig.2 RCR and Strehl Ratio comparing to the rms of residual wavefront in wave band of visible light

以中国科学院长春光学精密机械与物理研究所自主研发的1.23 m自适应光学望远镜对恒星目标的跟踪为例。望远镜口径为1.23 m，焦距为50 m，F数为40.7;波前探测器采用Shack-Hartmann，探测波段为500～700 nm，等效探测波长为632.8 nm;波前校正器采用自主研发的97单元压电陶瓷变形镜;成像波段为700～900 nm，成像等效波长为800 nm，成像相机像元尺寸为13 μm。对一颗恒星目标进行了观测，校正前后的RCR与波前残差σ如图1所示。可看出，校正前后RCR的均值分别为1.55%、3.07%;波前残差σ的均值分别为599 nm、340 nm。相对波前残差RMS。RCR也能较好地表征畸变波前的改善，是评价自适应光学系统实际分辨率的有效指标。1.23 m望远镜在长春地区对恒星和卫星等目标观测时，自适应光学系统校正后，波前探测器测量到的波前残差σ多在0.5λ以下。对应的RCR与波前残差σ与斯特列尔比之间的关系如图2、图3所示。从图2、图3可以看出，随着波前残差σ的增大，望远镜系统的RCR也迅速下降。当波前残差σ达到瑞利判据1/14λ，对应的 Strehl Ratio达到81.77%，系统已可认为是完善时，RCR只有61.54%。注意到式(9)中，RCR的系数际是望远镜系统对香农采样定理满足程度。望远镜光学系统是按650 nm设计的，因此，对于等效成像波长在800 nm的成像效果来说等于1的话，此时归一化到成像等效波长800 nm处的RCR为93.91%。说明:合理选取系统参数，对于望远镜自适应光学系统对于空间目标的实际分辨率指标RCR影响较大。只有0.655 3，这严重降低了RCR在σ达到瑞利判据时的值。如果

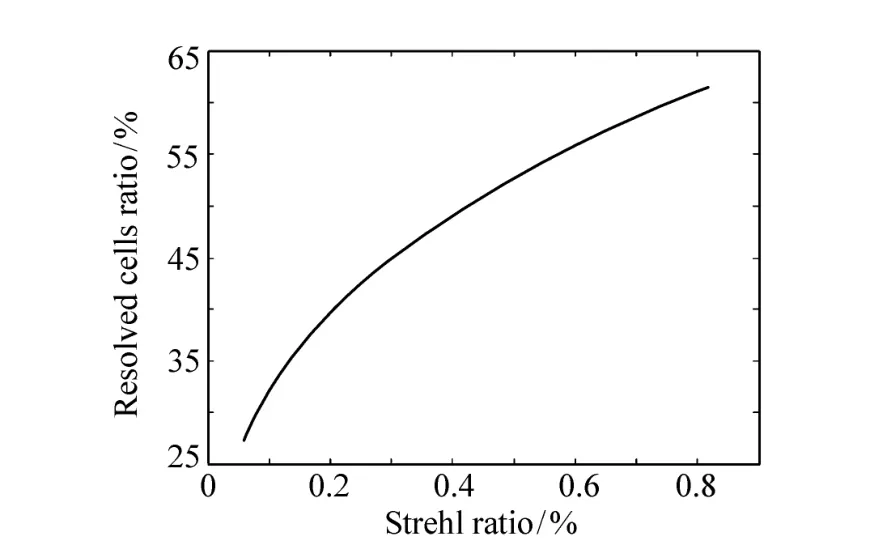
图3 可见光波段可分辨单元数比与斯特列尔比之间的关系Fig.3 RCR comparing to Strehl Ratio in wave band of visible light

欲提高RCR，可通过在满足香农采样定理的前提下，尽量增大，即减小f和增大p来实现。但对于设计参数固定的望远镜系统来讲，只能通过提高望远镜自适应光学系统的性能，进而增大Sdet来实现。由式(3)可知，减小f和增大p又会使得目标图像大小Ntheo减小。这说明目标图像大小Ntheo和实际分辨率RCR是一对互斥的物理量。如果以Ntheo和RCR的积作为指标考量的话，由式(9)和(3)可知，在自适应光学系统达到自身极限时，选择波长小的成像波段和减小F数是切实可行的路径。因此，在设计地基大口径望远镜时，需要根据预定的科学任务目标，对目标图像大小Ntheo和实际分辨率RCR两个指标平衡考虑。

综上可知，可分辨单元数比实质上是望远镜系统对香农采样定理的满足程度与自适应光学系统对空间目标的有效校正程度——斯特列尔比的函数。结合这两个指标的可分辨单元数比可全面反映望远镜对空间目标自适应校正后的实际分辨率，且物理意义更为直观。同时，可分辨单元数比是基于波前探测器测量到的波前特征——斯特列尔比推导得出的物理量，因此，可分辨单元数比适用于所有可以通过直接测量或间接计算如PD方法［14］得到成像端波前特征的情况。

3.2 可分辨单元数比的误差及大气弥散影响分析

对于设计参数固定的望远镜系统来说，RCR仅与波前探测器的波前测量误差σM相关。由误差传递理论可推得［15］，斯特列尔比Sdet对RCR的误差的误差传递系数为:

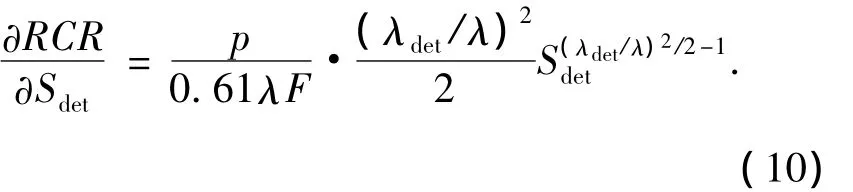
而Sdet的测量误差取决于波前探测器的测量精度。σM对Sdet的误差传递系数可由式(7)导出:

不同的自适应光学系统波前探测器可能不同。波前探测器采用Shack-Hartmann的σM的计算参见文献［7］，代入式(12)即可得到σM对RCR的误差传递系数;波前探测器采用剪切干涉仪时可同理导出。

目标在成像相机上的成像尺寸，由于受到大气弥散的作用，实际往往大于仅受几何光学限定的尺寸。

目标实际成像对系统张角的最大均方根s可用下式表征［16］:

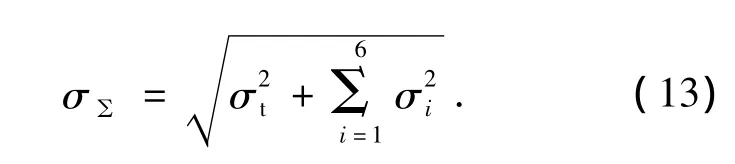
式中，σt为目标受几何光学限定的尺寸;σ1为光学系统成像引起弥散的均方根值;σ2为光学系统衍射分辨极限产生像点弥散的均方根值;σ3为像移造成角弥散的均方根值;σ4为探测器引起角弥散的均方根值;σ5为大气抖动造成像点弥散的均方根值;σ6为积分时间内跟踪系统造成角弥散的均方根值。但由可分辨单元数比的推导过程可知，目标的张角在获取RCR的过程中被抵消，因此大气弥散对于RCR实际并无影响。RCR与目标的物理尺寸、距离无关，是一个适用于所有空间目标，能够有效评价望远镜自适应光学系统对空间目标实际分辨率的指标。

4 结论

本文基于望远镜自适应光学校正后的角分辨率和系统参数，提出了一个能够实时描述空间目标自适应实际分辨率的指标——可分辨单元数比。可分辨单元数比可以全面反映望远镜自适应光学系统对于空间目标实际分辨率的描述，物理意义更直观;就可分辨单元数比的适用范围进行了讨论，其适用于所有可直接或间接获取成像端波前特征的情况;分析了可分辨单元数比的误差因素，其误差主要取决于波前探测器的测量误差;大气弥散对可分辨单元数比的表征无影响，且与目标的物理特征、距离无关。可分辨单元数比对地基大口径望远镜对空间目标的自适应光学实际分辨率的实时评价有重要参考作用。

［1］ 林旭东，薛陈，刘欣悦，等.自适应光学波前校正器技术发展现状［J］.中国光学，2013，5(4):337-351.LIN X D，XUE CH，LIU X Y，et al..Current status and research development of wavefront correctors for adaptive optics［J］.Chinese Optics，2012，5(4):337-351.(in Chinese)

［2］ 卫沛锋，刘欣悦，林旭东，等.自适应光学系统测试中大气湍流的时域模拟［J］.中国光学，2013，6(13):371-377.WEI P F，LIU X Y，LIN X D，et al..Temporal simulation of atmospheric turbulence during adaptive optics system testing［J］.Chinese Optics，2013，6(13):371-377.(in Chinese)

［3］ 饶长辉，姜文汉，凌宁.自适应光学系统对实际大气湍流波前的时域实际分辨率［J］.光学学报，2001，21(8):933-938.RAO CH H，JIANG W H，LING N.Temporal correction effectiveness of adaptive optical system for light wave atmospheric propagation［J］.Acta Optica Pticasinica，2001，21(8):933-938.(in Chinese)

［4］ 饶长辉，沈锋，姜文汉.自适应光学系统波前校正残余误差的功率谱分析方法［J］.光学学报，2001，20(1):68-73.RAO CH H，SHEN F，JIANG W H.Analysis of closed-loop wavefront residual error of adaptive optical system using the method of power spectrum［J］.Acta Optica Pticasinica，2001，20(1):68-73.(in Chinese)

［5］ LUKIN V P，FORTES B V.Partial correction for turbulent distortions in telescopes［J］.Applied Optics，1998，37(21):4561-4568.

［6］ 张以谟.应用光学［M］.北京:电子工业出版社，2008.ZHANG Y M.Applied Optics［M］.Beijing:Publishing House of Electronics Industry，2008.(in Chinese)

［7］ HARDY J W.Adaptive Optics for Astronomical Telescopes［M］.New York:Oxford University Press，1998.

［8］ 饶长辉.非Kolmogorov湍流情况下低阶校正自适应光学系统的性能研究［D］.北京:中国科学院，2000.RAO CH H.Performance analysis of low-order correction adaptive optical system for non-Kolmogorov turbulence［D］.Beijing:Chinese academy of science，2000.(in Chinese)

［9］ 林旭东，刘欣悦，王建立，等.137单元变形镜的性能测试及校正能力实验［J］.光学 精密工程，2013，21(2):267-273.LIN X D，LIU X Y，WANG J L，et al..Performance test and experiment of correction capability of 137-element deformable mirror［J］.Opt.Precision Eng.，2013，21(2):267-273.(in Chinese)

［10］ DIERICKX P.Optical performance of large ground-based telescope［J］.J.Modern Optics，1992，39(3):569-588.

［11］ CAGIGAL M P，CANALES V F.Generalized Fired parameters after adaptive optics partial wave-front compensation［J］.J.Opt.Soc.AM.A，2000，17(5):903-910.

［12］ 李勇.基于多尺度分解的多源图像融合算法研究［D］.长春:吉林大学，2010:11-15.LI Y.Multi-source image fusion based on multi-scale decomposition［D］.Changchun:Jilin University，2010:11-15.(in Chinese)

［13］ 傅瑶，孙雪晨，薛旭成，等.基于非下采样轮廓波变换的全色图像与多光谱图像融合方法研究［J］.液晶与显示，2013，28(3):429-434.FU Y，SUN X CH，XUE X CH，et al..Panchromatic and multispectral image fusion method based on nonsubsampled contourlet transform［J］.Chinese J.Liquid Crystals and Displays，2013，28(3):429-434.(in Chinese)

［14］ 王斌，汪宗洋，吴元昊，等.利用多通道相位差异波前探测法检测自适应光学系统非共光路像差［J］.光学 精密工程，2013，21(7):1683-1692.WANG B，WANG Z Y，WU Y H，et al..Calibration of no-common path aberration in AO system using multi-channel phase-diversity wave-front sensing［J］.Opt.Precision Eng.，2013，21(7):1683-1692.(in Chinese)

［15］ 费业泰.误差理论与数据处理［M］.北京:机械工业出版社，2000.FEI Y T.Error Theory and Data Processing［M］.Beijing:China machine press，2000.(in Chinese)

［16］ 牟达，王建立，陈涛.红外搜索跟踪系统作用距离的分析［J］.仪器仪表学报，2006，27(6):93-95.MOU D，WANG J L，CHEN T.Analysis for operating range of IR search ＆ track system［J］.Chinese J.Scientific Instrument，2006，27(6):93-95.(in Chinese)