关于包络与奇解的注记

邹志龙，涂 婷，王 成

(黄冈师范学院 数理学院，湖北 黄州 438000)



关于包络与奇解的注记

邹志龙，涂 婷，王 成

(黄冈师范学院 数理学院，湖北 黄州 438000)

给出了包络的不同定义并根据这些定义指出了包络与奇解之间的关系，然后根据这种关系用实例说明了用包络定义奇解的不相容性，最后指出用解的唯一性被破坏来定义奇解的合理性。

包络；奇解；定义；不相容性

一般谈到一阶微分方程的时候，都会涉及到包络与奇解，它们虽属不同范畴内的概念(包络属于几何学中的概念，奇解属于微分学中的概念)，但在几何意义方面它们却有着十分相似的地方。因此，一些微分方程的教材则利用包络与奇解之间的关系，通过研究包络的性质来定义奇解。有文献给出包络必不属于通解这一约束条件[1]；另有文献从包络线上的每一点均有曲线族中不同于它的曲线在该点与之相切来定义包络，从而定义奇解[2-5]；还有文献从两方面出发来定义包络，即曲线族中的每一条曲线均与包络线相切，而在包络线上的每一点均有曲线族中的一条曲线在该点与之相切[6-7]。由以上包络与奇解的研究现状可知这三种定义本身就存在不相容性，因此从几何方面来定义奇解必会给奇解的求解过程带来困扰。因而，本文从微分方程的角度出发，利用唯一性被破坏来定义奇解。

1 包络与奇解的定义

定义1[1]设给定单参数曲线族K(x,y,C)=0 其中C是参数，K(x,y,C)=0是x,y,C的连续函数。曲线族的包络是这样一条曲线，它本身不包含在曲线族内，但过曲线的每一点都有曲线族中的一条曲线和它在这一点相切。

定义2[2,3]设在平面上有一条连续可微的曲线L，如果对于任意的一点p∈L，在通解Ω(x,y,C)=0所对应的曲线族中均有一条曲线M(ΩM)通过p点并在该点与L相切，而且M(ΩM)在p点的某一领域内不同于L，则称曲线L为曲线族的包络。

定义3[6,7]曲线族的包络是这样的一条曲线，它与曲线族中的每一条曲线相切于一点或几点，而它由此类点组成。

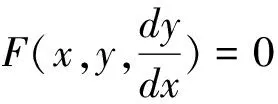
有一特解L∶y=φ(x),(x∈D)

如果对于每一点p∈L，在p点的任何邻域内方程有不同于L的解在p点与L相切，则称L是微分方程的奇解。

2 包络与奇解的关系

由包络与奇解的定义，即定义1、2、3、4的比较，可以得出以下结论：包络即为奇解。

3 用包络定义奇解时遇到的问题

由包络的三个定义可以得出三者之间具有以下不同：定义1说明通解的包络一定不包含在通解对应的曲线族内；定义2说明可能存在曲线族中的一条或几条曲线不与包络相切；而定义3则说明通解所对应曲线族中的每一条曲线都必须与包络相切。由于它们三者之间具有以上差别，故在求解奇解过程中相应的也会得出不同的结论，举例给予证明。

解：由微分法得方程的通解为y2+(x2-c)2=1，c≥-1或y=±1，如图1所示。

在平面直角坐标系中表示出方程解的图像，由图1可知当-1≤c<0时，通解对应的曲线与直线y=±1无交点，故由定义3知y=±1不是通解的包络，即不是方程的奇解。但当c≥0时，通解对应的曲线与y=±1相切，且在y=±1的每一点均有通解中的一条曲线在该点与之相切，由定义2知y=±1为通解的包络，即奇解。

注1 由例1知用定义2和定义3求奇解时会产生不同的结果，因此，定义2和定义3具有不相容性。

图1 为y2+(x2-c)2=1(c≥-1)的图像

例2 求微分方程y′3-4xyy′+8y2=0的奇解

解：用微分法可求得方程的通解y=c(x-c)2

令

Φ(x,y,c)=y-c(x-c)2=0

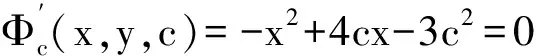
由C判别式[5]可得方程组

解得

由C判别曲线与奇解的关系可知，奇解一定属于C判别曲线；对于C判别曲线y=0而言，代入原方程可知其为方程的解；而由通解y=c(x-c)2可知当c=0时y=0，即y=0⊂y=c(x-c)2，因此由定义1知C判别曲线y=0不是方程通解的包络，即不是奇解。但分析通解y=c(x-c)2可知当c>0时，y≥0，又因为y′=2c(x-c)，所以当x>c时，y′>0，当x

注2 由例2知，定义1与定义2在奇解的判别过程中产生的结果亦不相一致，因此，定义1与定义2也具有不相容性。

4 奇解的另一种定义方法

从例1可以看出，方程除了有一通解y2+(x2-c)2=1，还有一解为y=±1。在所有的解中，除了y=0外，其余的解都满足唯一性，也就是说y=0所对应的积分曲线上的任何一点的唯一性均被破坏，满足这一性质的方程的解在微分方程中普遍存在，举例给予说明。

解：由初等积分法可求出微分方程的通解为y=(x+c)3

由例3的分析过程可知某些一阶隐式方程的个别解具有特殊意义，即该解对应的积分曲线上任一点的唯一性均被破坏，满足该特性的解称为奇解，因此可得出奇解的新定义：

定义5[3,5]如果微分方程存在某一解，在它所对应的积分曲线上的每一处解的唯一性都被破坏，则称此解为微分方程的奇解。

注3 若微分方程在整个f(x,y)有定义的区域D内满足解的存在与唯一性定理或在该区域的某个子区域D1内不满足解的存在与唯一性定理，且D1中的任意一点都不是方程的解，则方程一定无奇解。

用包络定义奇解是从几何角度定义的，由本文可知不同的定义会产生不同的结论，给奇解的求解带来了不便；而用唯一性被破坏来定义奇解是从微分方程本身的性质出发来定义的，避免了与其他学科的交叉。因此用唯一性被破坏来定义奇解较用包络定义奇解更加能够揭示奇解的奇异性特征。

[1] 王高雄,等.常微分方程(第2版)[M].北京：高等教育出版社，1983.

[2] 丁同仁,等.常微分方程教程[M].北京：高等教育出版社，1991.

[3] 任永泰,等. 常微分方程[M].沈阳：辽宁人民出版社，1984.

[4] 蔡燧林. 常微分方程[M].杭州：浙江大学出版社，1988.

[5] 东北师范大学常微分方程教研室. 常微分方程[M]. 北京：高等教育出版社，2005.

[6] 叶彦谦. 常微分方程讲义(第2版)[M].北京：人民教育出版社，1983.

[7] 高素志. 常微分方程[M].北京：北京师范大学出版社，1988.

(王菊平)

Notes about the envelope and singular solution

ZOU Zhi-long, TU Ting, WANG Cheng

(College of Mathematics and Physics, Huanggang Normal University, Huangzhou,438000, Hubei, China)

We discuss the relationship between the envelope and the singular solution according to the different definitions of the envelope. Examples are provided to indicate that the singular solution given in envelope has incompatibility. Finally, the definition of singular solution, based on which uniqueness is destroyed, has rationality.

envelope; singular solution; definition; incompatibility

O175.1

A

1003-8078(2014)03-0010-03

2014-04-30 doi 10.3969/j.issn.1003-8078.2014.03.03

邹志龙，男，湖北襄阳人，黄冈师范学院数学与应用数学专业学生。

王成，女，湖北黄石人，副教授，华中科技大学博士后，主要研究方向为随机系统稳定性。