基于状态反馈的单相电压型逆变器重复控制

贾要勤 朱明琳 凤 勇

（西安交通大学电力设备电气绝缘国家重点实验室 西安 710049）

1 引言

目前逆变电源的应用越来越广泛，对其性能的要求也越来越高。对于高性能逆变电源，高稳定性和对扰动的快速响应都是很重要的指标要求。而且目前高速DSP 的迅速发展使一些比较复杂的控制算法也能用在逆变电源的控制上。目前常用的数字控制算法包括如下几种：单环PID 控制、电压电流双环控制、多变量状态反馈控制、无差拍控制、重复控制等。

重复控制对于未知的干扰信号，通过对前几个周期的波形处理，利用已知的信息对当前的控制进行校正，从而获得良好的波形跟踪控制效果。因此重复控制可以对系统实现无静差跟踪，提高了系统的跟踪精度[1,2]。重复控制如果同其他控制算法相结合，可以改善其动态性能及控制特性。但是很明显由于重复控制是利用周期进行控制的算法，在控制系统的闭环回路内存在一个指令信号的周期延时，所以必须提高重复控制的瞬时响应速度[2,3]。

文献[4]提出的重复控制算法对死区影响及其他周期性扰动有明显抑制作用，而且能消除跟踪误差，使系统输出达到无静差，而且该方法克服了重复控制固有的滞后调节特性，减小了稳态误差。

文献[5]提出了一种改进重复控制算法。给出了低通滤波器转折频率的选择标准，推出了延迟时间与截止频率之间的关系，改进了传统重复控制器内模的延时时间。但该方法不能实现参数自调整，实际得到的参数与理想值并不一致。

本文主要研究重复控制算法在逆变电源中的应用，包含了基本重复控制的数字实现及其稳定性和瞬时响应速度的分析，并且针对重复控制动态响应存在的问题，提出了利用状态反馈控制对其进行改进的算法。通过对控制变量的选择，采用包含积分环节的状态反馈控制对逆变器的输出电压进行控制，有效抑制了控制系统的闭环回路内存在的指令信号的周期延时，更好的改善逆变器在突加负载时出现的电压大幅度跌落的问题[6]，最后通过实验比较了基本重复控制算法和改进的重复控制算法，验证了改进重复控制算法的优越性。

2 单相全桥逆变器的建模分析

本文所使用的单相逆变器的结构图如图 1 所示，其中Vdc是直流侧电压，VT1、VT2、VT3、VT4为全控型器件IGBT，r为滤波电感的等效电阻和系统阻尼因素的综合等效电阻[7]，电感L和电容C组成低通滤波器，U为逆变桥输出的脉冲电压，iL为流过滤波电感的电流，vC为滤波电容两侧的电压也就是逆变器的输出电压，I为负载电流。

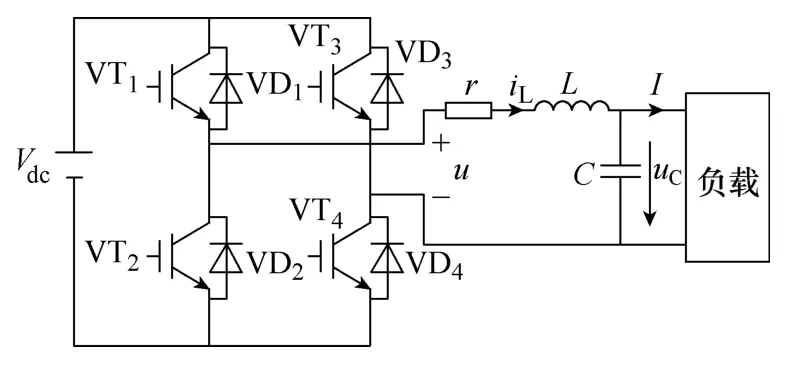
图1 单相逆变器的结构图Fig.1 The structure of the single-phase inverter

完全确定系统行为的数目最小的变量称为状态变量，本文中选择电容电压vC和电感电流iL为状态变量，取电容电压作为逆变器输出，系统状态方程为

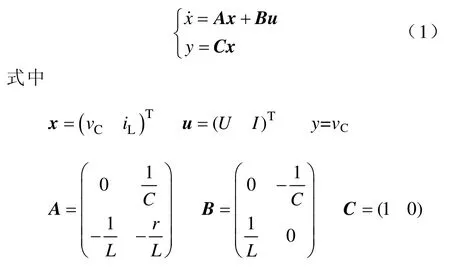
如果忽略开关器件及死区时间造成的非线性影响，逆变桥和SPWM 调制器可以看作是一阶惯性环节，数学式可写成

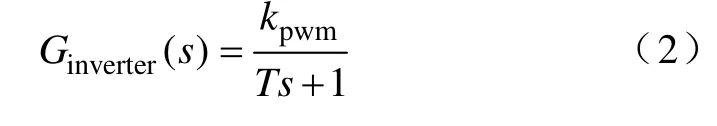
式中kpwm——逆变桥和SPWM 调制器的等效增益；

T——开关动作周期。

一般开关动作周期很小，此时Ts+1≈1，且分析中常把kpwm近似为1，比例系数可在控制器中调整[8]。单相逆变器的主电路结构图如图1 所示。由此可得到空载时逆变器传递函数

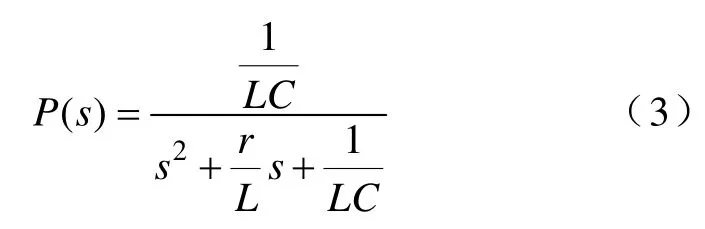
由式（3）可以看出，逆变器模型被简化成了一个简单的二阶模型，其中自然振荡频率阻尼比

数字控制中经常使用的采样过程是使用零阶保持器，把采样时刻的瞬时值作为在该采样周期内的采样值[9.10]，由系统的连续状态方程式（1）得到系统离散状态方程的矩阵表达式如下：

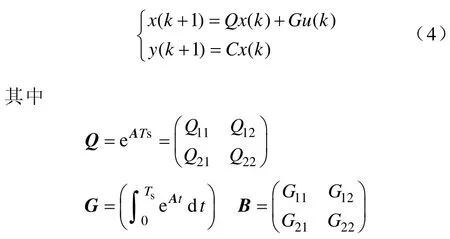
式中，Ts为采样周期。

3 基本重复控制算法

重复控制器是以内模原理为基础，把能产生固定周期的重复信号发生器放置在闭环系统内达到对周期信号无静差跟踪目的的一类控制器。由内模原理可得，若把这样的函数发生器放在闭环内就可以对周期为T的外激励信号进行无静差跟踪。这个周期函数发生器又被称作重复补偿器，重复控制系统就是指包含重复补偿器的系统，图2 为这种控制系统的结构图。

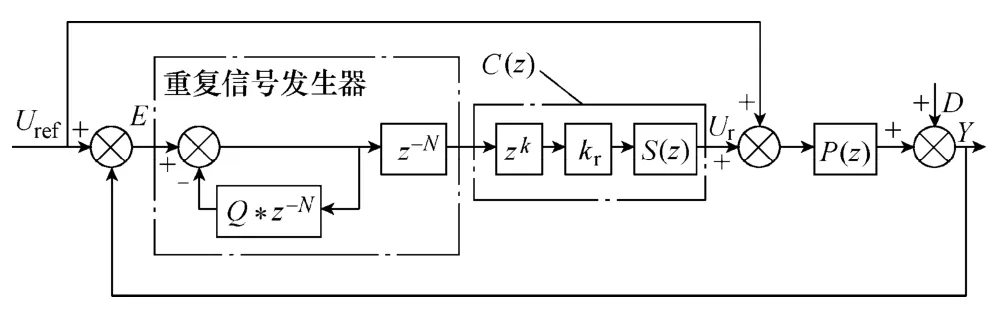
图2 “嵌入式”重复控制系统结构图Fig.2 The structure of the embedded repetitive control system

Q(z)是一个低通滤波器，一般取一个小于1 的常数，用以增加系统的稳定性。重复控制器的每个周期的输出增量是上一个周期输出量的Q倍。当输入量减小为输出量的（1-Q）倍时，累加过程将会结束。此时系统的稳态误差将会变为输入量的（1-Q）倍。只有在Q=1 时，系统才能达到无静差跟踪。|Q| ＜1 时，提高了系统的稳定性，但却降低了系统的稳态精度[9-11]。

周期延时环节使控制信号延时一个指令信号周期，虽然这一环节严重影响了系统的动态响应性能，但是为了使补偿器中相位超前环节能够在物理上实现，这一环节又是必需的不可缺少的[9-11]。

补偿器C(z)是重复控制系统的核心，其设计与控制对象P(z)有关。本文设计的基本思想是把补偿器分为两部分，即幅值补偿和相位补偿，主要补偿对象是系统的中低频段。由于系统在高频段模型的准确精度不够，补偿相对困难。因而补偿器中采用低通滤波器滤除控制对象高频分量和谐振峰，设置比例环节用来保证系统的稳定以及对中低频段的跟踪精度。采用zk对系统进行相位补偿，保证中低频段为零相移[9-11]。基于以上原理可得补偿器C(z)的数学表达式

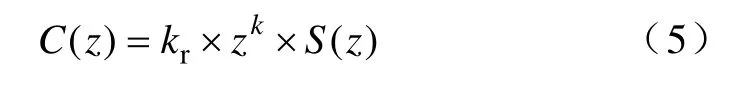
式中S(z)——低通滤波器；

kr——比例环节；

zk——相位补偿器。

针对图2 的基本重复控制系统的特例,即没有前向通道的情况，令G=CP，控制系统的误差到指令信号的传递函数为

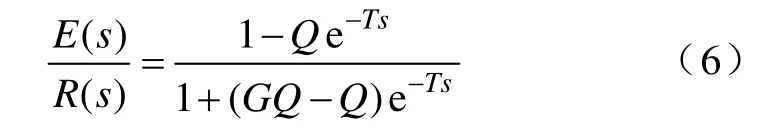
假设此时系统的干扰信号D=0，在|GQ-Q|＜1的情况下，系统的误差表达式可以表示如下：

所以可得下式

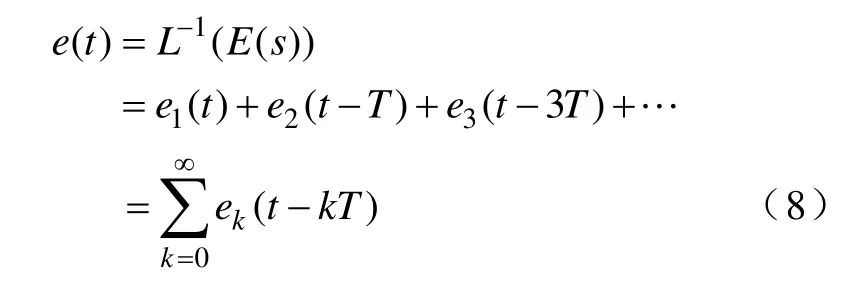
由上式可以看出若采用图2 结构，系统从第二周期的误差开始与系统的控制对象和控制器的参数有关，而第一周期的误差e1直接就是指令信号，与重复控制器的参数无关。系统的瞬态响应滞后指令信号一个周期，在实际应用中这将是不允许的。因而在基本重复控制系统中引入指令信号前馈控制。第二周期的误差e等于e1和e2的稳态响应的和，以后各周期的误差可以类推。由于在补偿中尽量保证了控制器的低频增益，控制对象的传递函数G近似为1，因而e3，e4，e5近似为零[12]。

为了估计系统的暂态响应性能，由线性系统输入输出关系[13]可得e2的无穷范数如下式所示

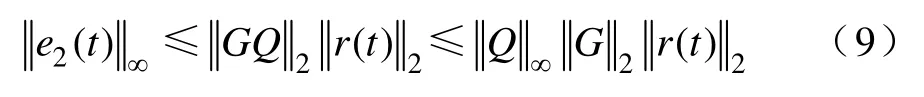
对于一个指定的系统，第二周期的响应的峰值是和||Q||∞有关的，而且此时系统的误差是系统加入重复控制器后的最大值，此后系统的误差在逐周期减小。

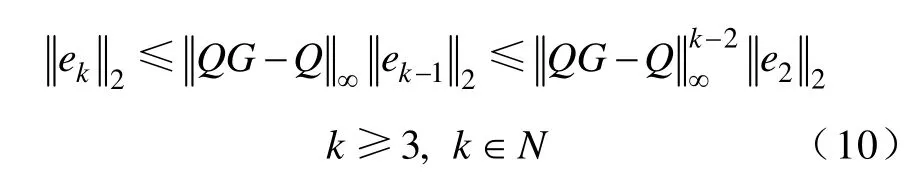
对于e3，…可以看出后面各周期的误差满足如下关系式的情况下，系统稳定，这和第4 部分引入滤波器Q的系统的稳定条件是一致的，系统每个周期的误差衰减率为在

4 改进的重复控制算法

由于重复控制系统中的周期滞后环节导致系统的动态响应不好。因而考虑重复控制系统和其他瞬时值控制算法构成复合控制提高系统的动静态性能。本文采用状态反馈算法与其结合，改进算法的结构图如图3 所示[13]。

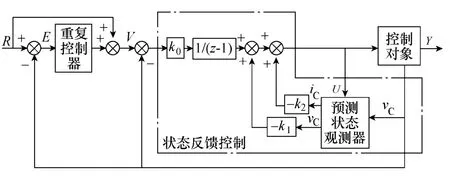
图3 改进重复控制系统结构图Fig.3 The structure of the modified repetitive control system

4.1 控制变量的选择

本文选择电容两侧电压和流过电容的电流为状态变量，这会更好的改善逆变器在突加负载时出现的电压大幅度跌落的问题[14]。这是因为如果选择电感电流为状态变量，当负载发生变化时，由于电感具有维持流过它的电流瞬时不变的特性，根据基尔霍夫电流定理这将会导致电容电流发生较大幅度的变化，从而会导致电容两侧电压变化幅度较大。而采用电容电流为状态量，负载电流就被包含在电流控制环内，电流环便可以及时地对负载扰动进行调节，控制系统对于负载扰动有很强的抑制。实验结果也很好的证明了这一点。

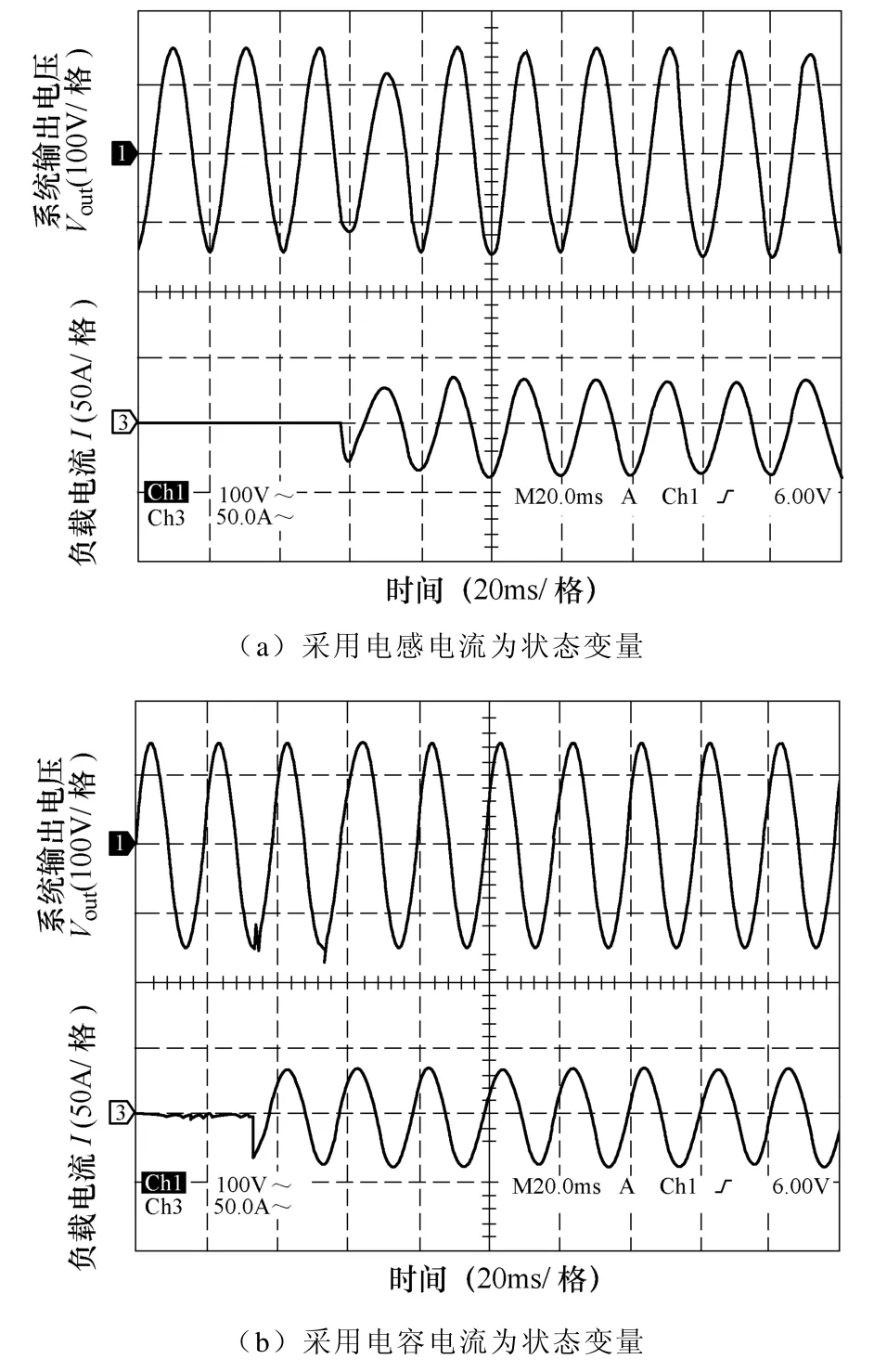
图4 选择不同状态变量的实验结果Fig.4 The experimental results in the different state variables

4.2 状态反馈控制器设计

逆变电源的自然动态特性不好的主要原因是由于逆变器z域表达式的主导极点太靠近单位圆，自身的阻尼比太小。所以考虑采用基于极点配置的状态反馈方法配置控制对象的主导极点，提高控制对象的阻尼比[15,16]。

考虑到当负载刚发生突变时，相当于对系统突加了一个阶跃性的干扰信号，因而在状态反馈中加入积分环节[17]，提高系统对干扰的抑制特性。对于二阶系统，一般认为ξ=0.707 时系统的动静态品质比较好，考虑逆变器带载后一般会向阻尼比增大的方向移动，在本文中选择阻尼比为0.539，系统配置后的自然振荡频率为5 000rad/s。此时闭环系统配置的极点在s域为-23 025,-2695±4 212i，在z域为0.1,0.697±0.312i。此时系统的反馈增益矩阵为(0.77 2 30)。补偿后的系统的开环和闭环的z域表达式为

4.3 状态观测器

采用预测状态观测器可以抵消执行控制算法导致的延时，尤其在当算法执行时间和系统采样时间相比不大的情况下，超前一拍预测就显得非常重要。

由控制理论可知本系统完全可观，可以任意配置系统极点，所以本系统可以使用状态观测器实现逆变系统的一拍滞后补偿。

由被控对象的离散状态方程可得到重构以后的系统状态方程为

对观测器引入输入反馈，闭环系统状态观测器表达式为

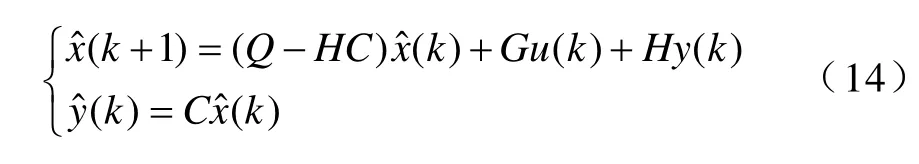
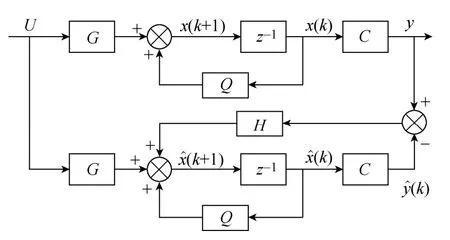
图5 含预测状态观测器的控制系统的结构图Fig.5 The structure of the control system including a predictive state observer

预测状态观测器的结构图如图5 所示。输出反馈仅与状态观测器的误差收敛速度有关，预测观测器的极点设计和状态反馈的参数设计可独立分开进行[18]。所以预测状态观测器的极点选择只考虑误差收敛速度即可，依据参数设计经验本文选择观测器的极点为原控制对象谐振点处频率的4 倍左右。

由于已使用了状态反馈对原系统的极点进行了配置，消除了系统的谐振峰，重复控制的设计被简化了很多。补偿器中仅需要一个比例环节，一个二阶低通滤波器和一个相位补偿环节即可。这里选择二阶低通滤波器的阻尼比ξ=1，自然振荡频率为5 000rad/s，稍大于逆变器被补偿后系统的自然振荡频率，比例系数选为 1，超前环节的阶数为7。

通过Matlab 中的仿真模块可以对两种方法的误差收敛进行仿真，如图6 所示。

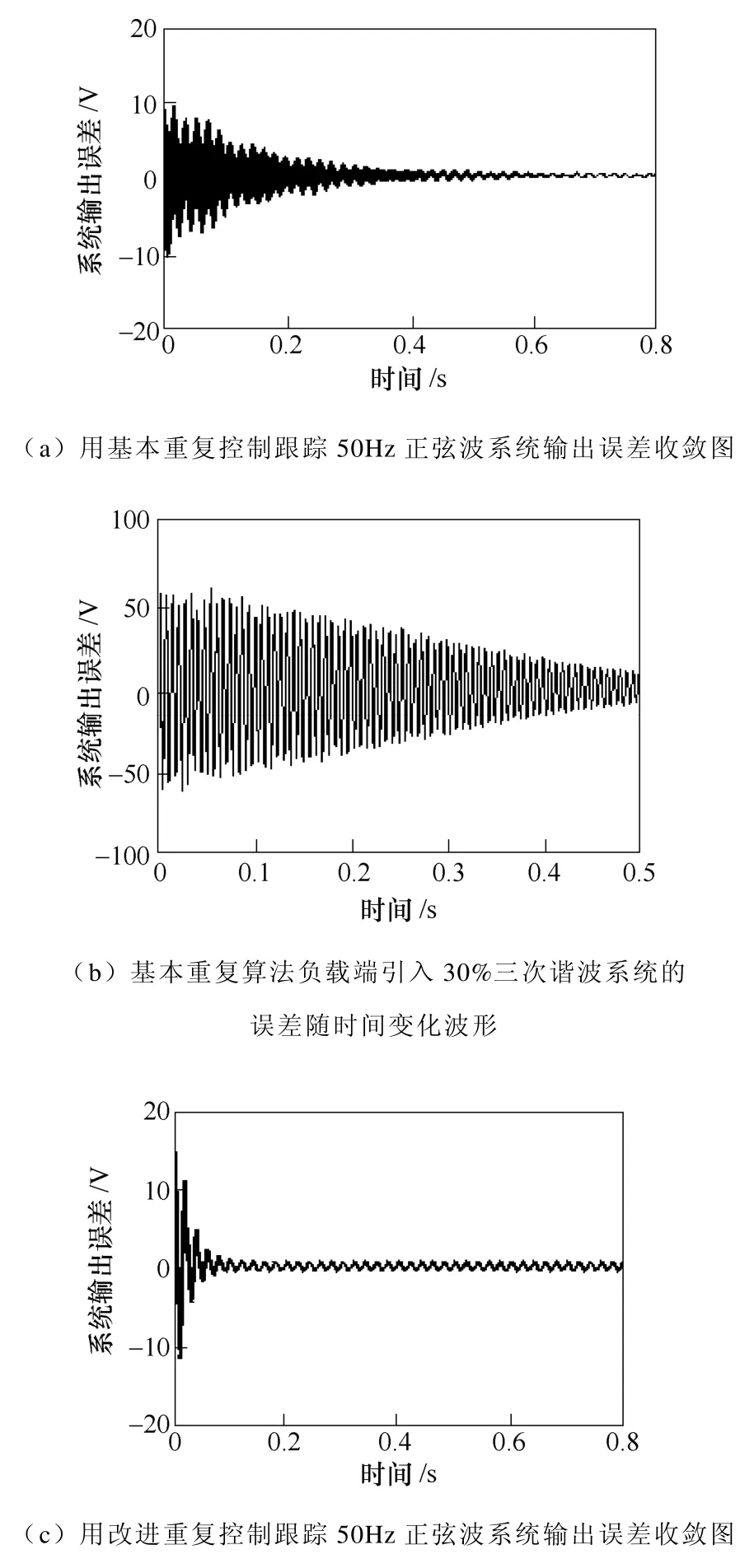
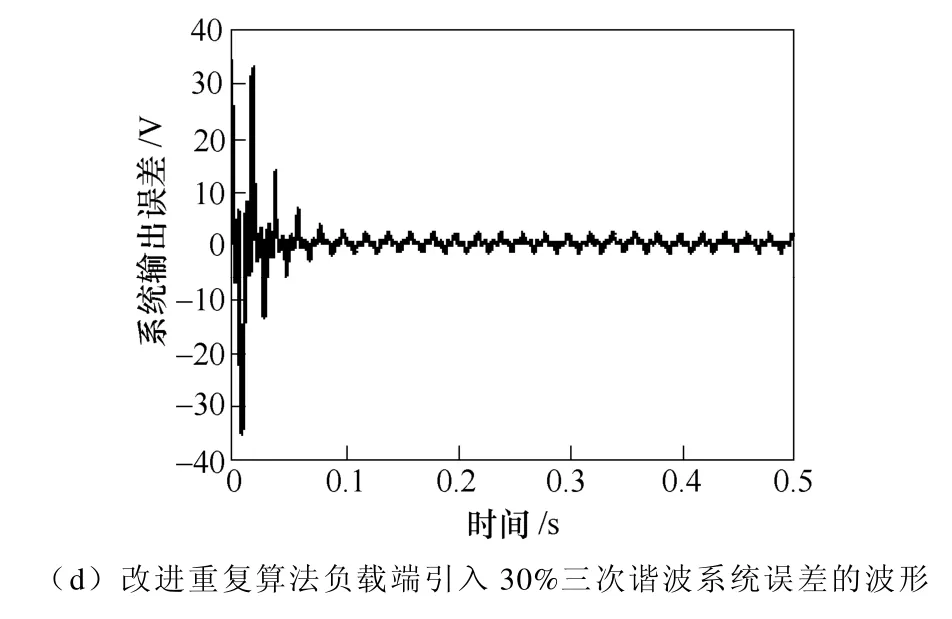
图6 误差收敛仿真结果Fig.6 The simulation results for convergence error

5 实验研究

本文中所使用系统参数如下表所示，实验平台如图7 所示。主要包含这几个方面：市电、三相调压器、二极管不可控整流电路、单相全桥逆变器、负载、电源、DSP 控制板和示波板。主电路采用交直交变换电路，把电网的三相交流电通过调压器和不可控整流电路得到直流电Vdc，然后经过单相全桥逆变器和LC 滤波器得到所需要的正弦电压，逆变器中的开关器件为IPM 模块，开关的通断由DSP模块输出的控制信号决定。DSP 控制板和PC 机之间采用光纤通信，用来实现程序的编译下载等。

表 单相全桥逆变器系统参数Tab.The parameters of single-phase full-bridge inverter

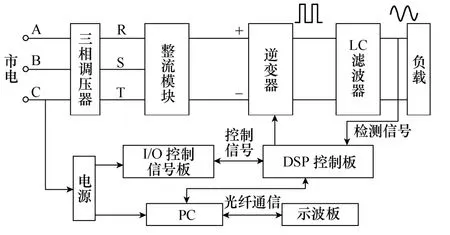
图7 单相逆变器实验平台Fig.7 Single-phase inverter experimental platform

图8 为实验结果，由图8 可见采用改进的重复控制算法系统对指令信号跟踪动态响应得到较大提高，指令信号的频率越高，对比就越明显。当系统的负载端发生突变时，采用改进的重复控制算法时系统的恢复时间比较短，动态特性较好。

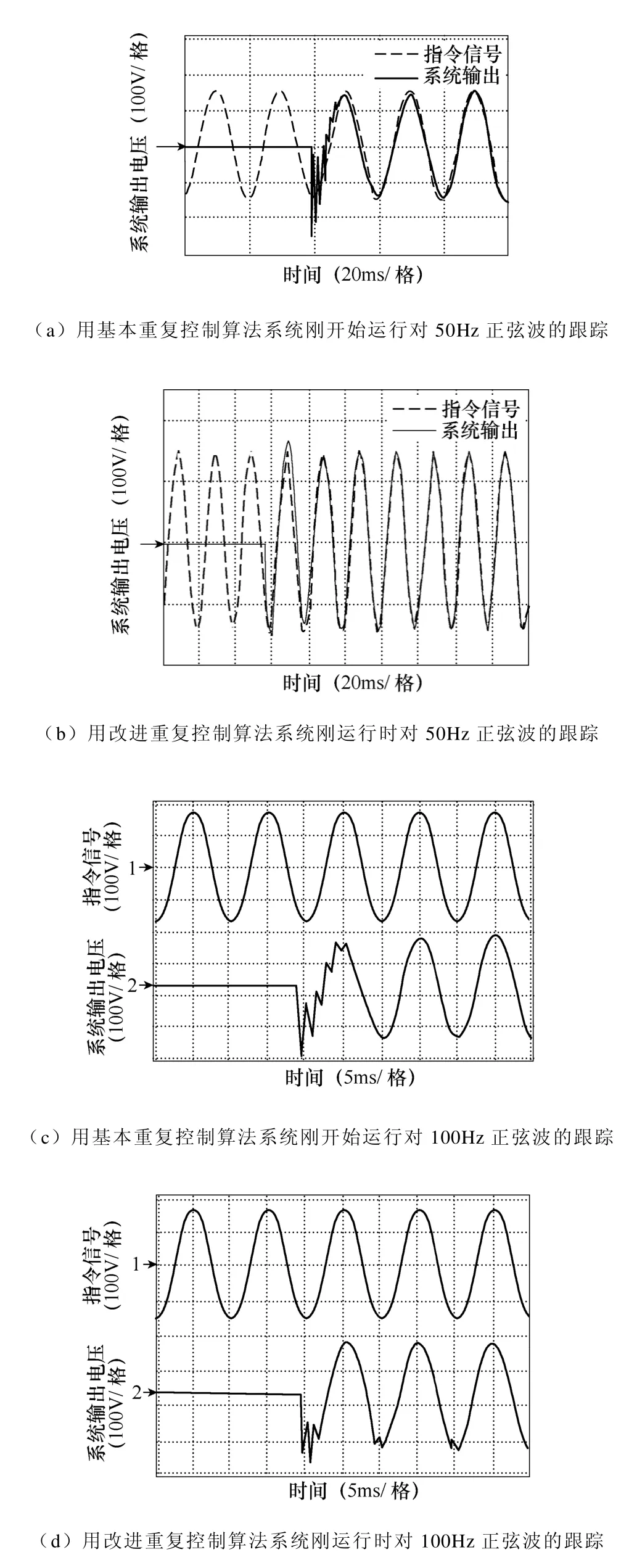
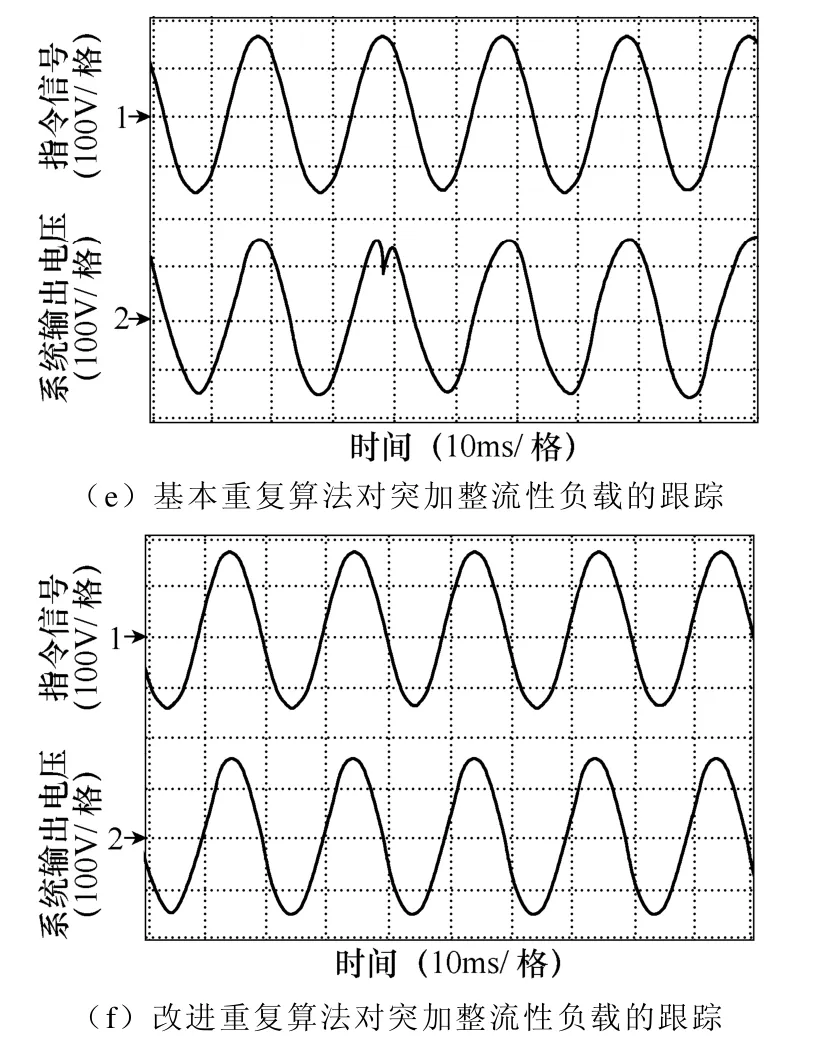
图8 对突加非线性负载的跟踪效果Fig.8 The tracking results with added non-linear load

图9 为使用改进重复算法负载端引入30%三次谐波时系统误差随时间变化的实验波形。实验结果与仿真结果吻合。

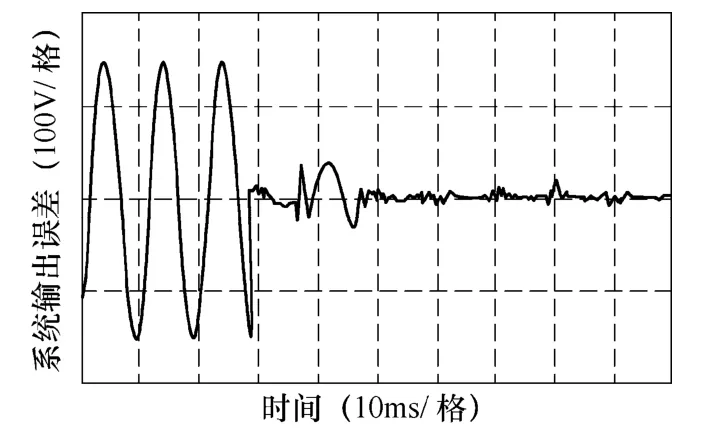
图9 改进重复算法引入30%三次谐波时系统误差的实验波形Fig.9 The experimental waveform of system error with third harmonic

图10 为给定信号频率突变时动态过程的实验波形。频率突变时，改进重复算法可以实现对于指令信号的跟踪。

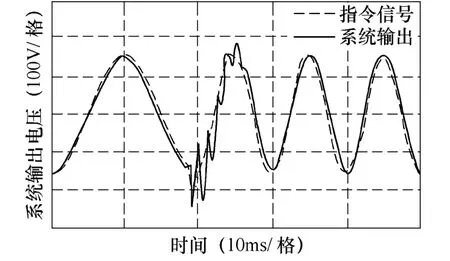
图10 给定信号频率突变时动态过程波形Fig.10 The dynamic response under mutation of signal frequency

6 结论

本文对基本重复控制以及带有状态反馈的重复控制进行了全面的比较研究，得出带状态反馈的重复控制兼顾基本重复控制固有优势的同时，其动态性能上也有了很大的改善。在电压型逆变器控制上有很好的借鉴作用。

[1]陈宏.基于重复控制理论的逆变电源控制技术研究[D].南京:南京航空航天大学,2003.

[2]朱明琳.单相电压型逆变器重复控制研究[D].西安:西安交通大学,2010.

[3]郑崇峰.CVCF 逆变器重复控制策略研究[D].杭州:浙江大学,2006.

[4]吴杰,茆美琴,苏建徽,等.基于重复控制算法的光伏并网逆变器的研究[J].电子设计应用,2005(2):103-106.Wu Jie,Mao Meiqin,Su Jianhui.Research on photovoltaic grid connected inverter based on repetitive control algorithm[J].Electric Design &Application World,2005(2):103-106.

[5]马迎召.基于改进重复控制的有源电力滤波器研究[D].长沙:长沙理工大学,2010

[6]张凯,彭力,熊健,等.基于状态反馈与重复控制的逆变器控制技术[J].中国电机工程学报,2006,26(10):56-62.Zhang Kai,Peng Li,Xiong Jian,et al.State-feedbackwith-integral control plus repetitive control for PWM inverters[J].Proceedings of the CSEE,2006,26(10):56-62.

[7]王兆安,黄俊.电力电子技术[M].北京:机械工业出版社,2002.

[8]张崇巍,张兴.PWM 整流器及其控制[M].北京:机械工业出版社,2003.

[9]谢力华.逆变电源数字控制技术及其并联控制策略的研究[D].西安:西安交通大学,2001.

[10]张凯.基于重复控制原理的CVCF-PWM 逆变器波形控制技术研究[D].武汉:华中科技大学,2000.

[11](日)中野道雄,山本裕.重复控制[M].吴敏,译.湖南：中南工业大学出版社.1994.

[12]游志青.基于重复控制技术的数字式逆变电源的研究[D].南京:南京航空航天大学,2003.

[13]Shinji H,Yutaka Y.Repetitive control system :a new type servo system for periodic exogenous signals[J].IEEE Transactions on Automatic Control,1988,33:659-668.

[14]Garimella S S,Srinivasan K.Transient response of repetitive control system[C].Proceedings of the 1994 American Control Conference,1994,3:2909-2913.

[15]Doyle J C,Francis B A,Tannenbaum A R.Feedback control theory[M].Macmillan Publishing Company,1992.

[16]G Josep M,Luis Garcia de Vicuna,Jaume M,et al.Integral control technique for single-phase UPS Inverter[C].Proceedings of the IEEE International Symposium Industrial Electronics,2002,4:1043-1048.

[17]李志江.逆变电源控制方案的研究与实现[D].杭州:浙江大学,2004.

[18]田斌.SPWM 逆变器带极点配置的重复控制研究[D].武汉:华中科技大学,2004.