辅助电流有源调整的新型ZVS 全桥变换器
陈 仲 刘沙沙 汪 洋 史良辰
(南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016)
1 引言
全桥PWM 变换器拓扑结构在中大功率变换场合一直是国际和国内学者们的研究热点[1-7]。为了提高效率,实现节能减排,近年来研究学者们又提出了多种新型的软开关拓扑方案。其中零电压开关(Zero-Voltage-Switching,ZVS)PWM 移相全桥变换器通过利用变压器漏感和功率开关管寄生电容的谐振达到实现开关管ZVS 的目的。但由于漏感往往较小,滞后臂在较轻负载条件下的ZVS 实现较为困难,这就使得传统的移相全桥变换器在轻载时效率较低,电磁干扰(Electromagnetic Interference,EMI)等问题也会随之而来。
为获得滞后臂宽范围的ZVS,在变压器一次侧可串入大的谐振电感,但这会引起严重的二次侧占空比损失及一次侧环流损耗。将线性谐振电感替代为饱和电感的方法,很好地降低了占空比损失及一次侧环流损耗,而饱和电感的不足之处在于体积大,发热严重[8]。加入并联型无源辅助电路的全桥变换器[9,10],将额外加入的谐振电感从主功率传递路径中移出,同样实现了滞后臂宽范围ZVS 的目的,且占空比损失及环流损耗小。但无源辅助网络能量大小很难掌控,其导通损耗较为严重,变换器效率提升受到制约。文献[11,12]中滞后臂并联了有源辅助网络,在滞后臂换流前控制辅助开关管导通一段时间,使辅助电感存储一定的能量,拓展了变换器软开关范围,但其辅助开关管的导通时间是设定不变的,重载时辅助网络能量过剩,导通损耗大。文献[13]中通过检测负载电流进而计算出辅助开关管的导通时间,全负载范围实现了滞后臂的ZVS,且在整个负载范围内将辅助网络导通损耗控制在较低水平,但其辅助开关管控制电路较为复杂,实现困难。文献[14,15]提出了一些基于无源辅助网络的全桥变换器,该系列拓扑的特点是其辅助网络产生的能量能够随负载变化。但是加入的辅助支路与主电路存在串联关系,电流应力相对较大,且变换器的可靠性一定程度上受到了影响。
基于以上研究背景,本文提出一种辅助电流自调整的新型移相全桥ZVS 变换器,在传统的全桥变换器中加入与滞后臂并联的有源辅助网络,辅助网络既不影响主功率的传输,且保证了滞后臂在全负载范围内实现ZVS,辅助网络能量可随负载的变化进行自调整,降低了导通损耗,同时辅助开关管控制简单。
本文首先深入分析该变换器的工作过程,并对该变换器拓扑作进一步简化,之后给出重要参数设计原则,最后通过一台1kW/54V 的样机验证该变换器的正确性和实用性,并给出相应的结论。
2 新型变换器的工作过程分析
新型零电压开关(ZVS)PWM 移相全桥变换器拓扑结构如图1 中所示,它由传统的全桥变换器和与滞后臂并联的有源辅助网络组合而成。其中传统的全桥拓扑结构中,Q1、Q3为超前管,Q2、Q4为滞后管。辅助网络由以下器件构成:辅助开关管Q5、Q6,辅助电感La,辅助变压器以及辅助电容Ca。辅助变压器Tra的一次绕组一端与主变压器Tr的一次绕组中心抽头处相连,另一端与辅助电容Ca相连接。辅助变压器磁心体积较小,这是因为它不参与能量传输,仅仅提供辅助开关管Q5、Q6的控制信号。
为了便于分析,有如下假设:①电路拓扑中涉及的所有器件均是理想的;②Lf足够大,输出电流可以看做是恒定不变的;③C1=C2=Clead,C3=C4=Clag,这里忽略辅助开关管寄生电容的作用;④辅助变压器匝比为Npa:Nsa=nA,nA应满足辅助开关管的驱动要求,忽略辅助变压器一次电流对电路工作的影响;⑤辅助电容Ca足够大,其电压vCa基本不变,保持在Vin/2。
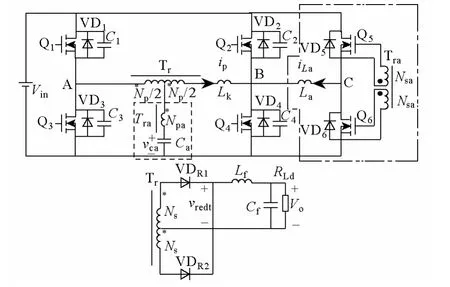
图1 提出的ZVS 全桥变换器拓扑Fig.1 Proposed ZVS PWM full-bridge converter topology
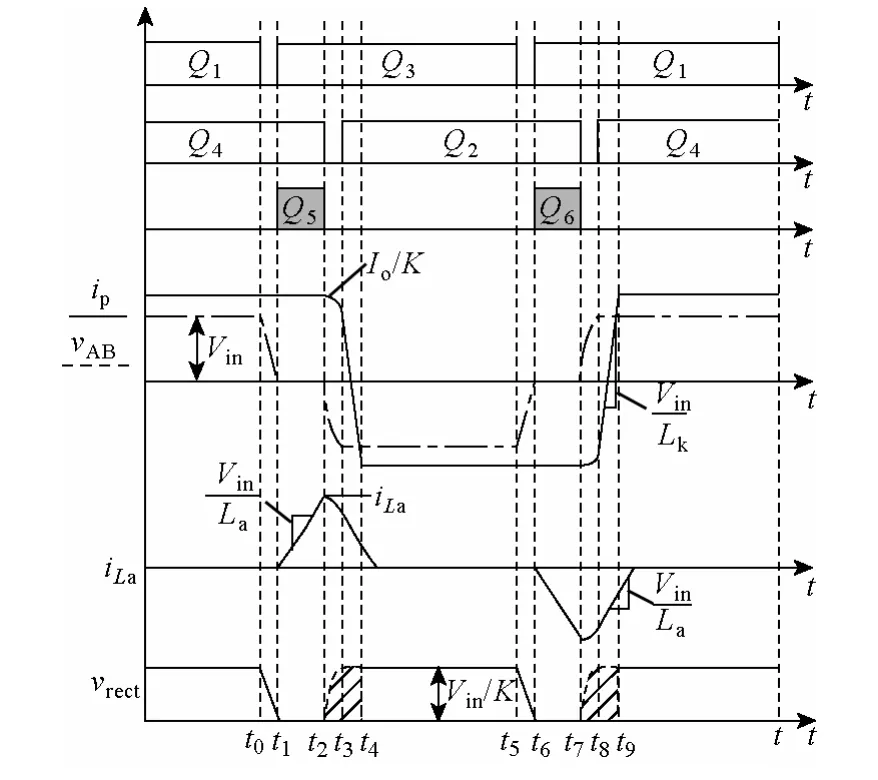
图2 新型ZVS 全桥变换器的主要波形Fig.2 Key waveforms of new ZVS PWM full-bridge converter
图2 和图3 分别给出了新型变换器的主要工作波形和该变换器在各开关时段下的对应等效电路。
(1)时段1[t0~t1],如图3a 所示。t0时刻之前,一次侧不断地向二次侧传递能量。Q1和Q4同时导通,Q2和Q3均关断,一次电流ip=Io/K(K=Np/Ns)维持不变,vAB=Vin,整流二极管VDR1承载所有的负载电流,VDR2截止。此时由于辅助变压器两端电压维持在零,两辅助开关管均关断。t0时刻Q1的驱动信号消失,如图3a 所示。电流ip从Q1中转移到C1和C3支路中,桥臂中点电压vAB由Vin逐渐减小。在这个时段里,储存在Lk和Lf中的能量给C1充电,同时给C3放电。因C1和C3的缓冲作用,Q1是零电压关断。由于一次电流维持不变,在t1时刻,C3两端的电压线性下降到零,Q3的反并联二极管 VD3自然导通,Q3可实现零电压导通。
(2)时段2[t1~t2],如图3b 所示。在VD3导通之后,开通Q3,Q1和Q3驱动信号之间的死区时间td(lead)>t01。A 点电位下降为零,由于B 点电位此时也为零,所以vAB=0,一次侧不再向负载传递能量。这个阶段辅助变压器二次电压为Vin/2nA,辅助开关管Q5栅源极承受正向电压Vin/2nA而导通,此前辅助电感电流为零,在辅助电感的缓冲下,此时辅助开关管Q5近似零电流导通,辅助开关管Q6栅源极因承受反向电压−Vin/2nA而截止,此时iLa从零开始增加,辅助电感电流可表示为
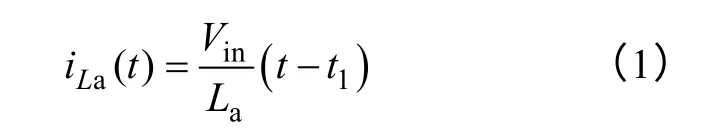
t2时刻,辅助电感La储存的能量可用下式来表示:

式中,D 为电路的工作占空比;Ts表示开关周期。
从式(2)可以看出,辅助电感La储存的能量取决于辅助电感、输入电压和电路工作占空比D 的大小,而在整个负载范围内实现滞后臂ZVS 所需的能量有所不同。一般而言,轻载时实现滞后臂ZVS所需的辅助能量要大于重载时的情况。而这里辅助电感储存的能量与负载电流密切相关,负载电流逐渐减小时,电路工作占空比D(D≥0.5)也随着减小,辅助电感储存的能量反而增加,即辅助电感储存的能量可以随着负载电流的变化而自适应的调整,有利于减少电路导通损耗。而占空比D<0.5 的情况,将会在本文第4 部分进行讨论。
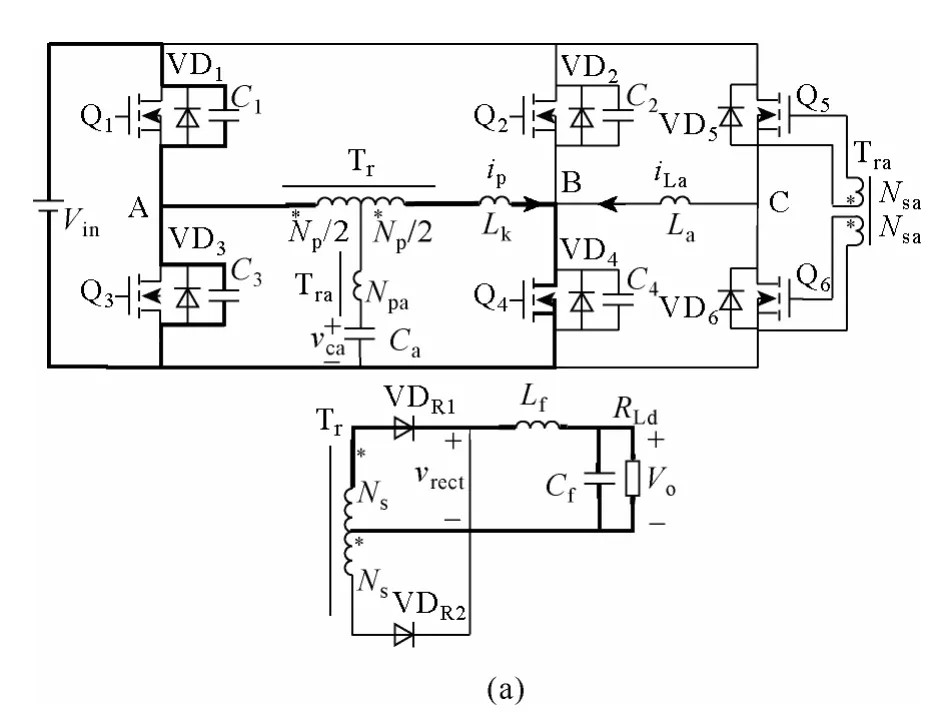
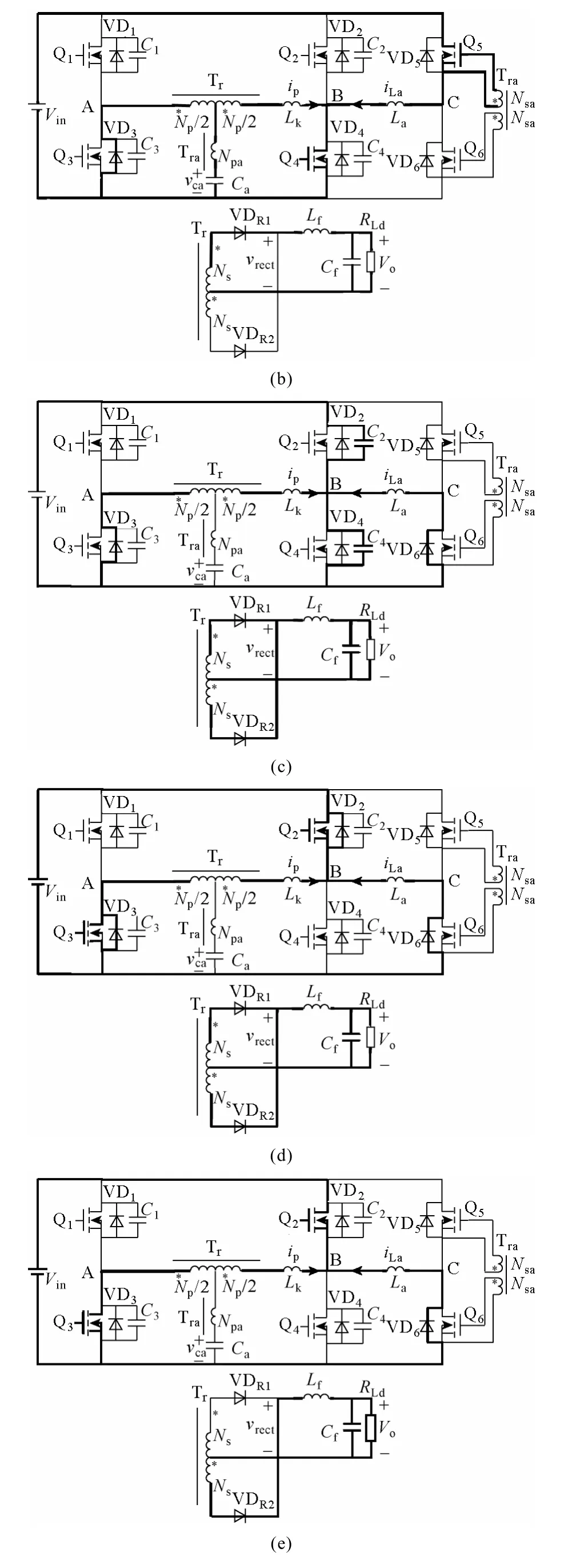
图3 各开关模态的等效电路Fig.3 Equivalent circuits of each operation stage
(3)时段3[t2~t3],如图3c 所示。在t2时刻,Q4驱动信号消失,流入滞后桥臂的一次电流和辅助电流同时给C4充电,同时给C2放电,Q4是零电压关断。一次电流下降,并且不足以提供输出负载电流,二次整流二极管VDR1、VDR2同时导通续流,变压器一二次电压都被钳位于零,vAB直接加在了变压器漏感Lk上。这个阶段里辅助电感电流iLa可近似看成恒流源,漏感Lk,电容C2、C4谐振工作。则一次电流ip和开关管Q4的端电压可以表示如下:
式中,ILa为 t2时刻辅助电流的初始值;。
t3时刻,C2的端电压下降为零,C4的两端电压上升至Vin,VD2自然导通。
(4)时段4[t3~t4],如图3d 所示。VD2导通后,Q2的零电压导通条件已满足。Q2、Q4驱动信号之间的死区时间td(lag)>t23。Q2导通后,vAB=−Vin。此时二次侧两个整流管仍同时导通,继续续流,变压器一次电压为零,输入电压Vin反向直接加在漏感Lk上,一次电流ip快速下降并反向增大。辅助电感此时承受反向电压−Vin,辅助电流iLa线性减小。
(5)时段5[t4~t5],如图3e 所示。在t4时刻,一次电流反向增加到折算后的负载电流,即ip=−Io/K,VDR1截止,VDR2承载所有的负载电流,一次侧向二次侧传递能量。此阶段,辅助电流仍线性减小,直至到零。t5时刻之后变换器进入后半个周期,其工作情况与上述半个周期相同,这里不再详细描述。
3 拓扑简化
实际应用中,为了避免桥臂直通,各桥臂上下管驱动信号之间设置了死区,但其相对于开关管的导通时间很短,甚至可以忽略,因此可对图2 中相关波形进行简化,如图4 所示。图4 中同时给出了电路工作于不同占空比D 时的简化波形。可以看出,负载较重时,D 较大,对应的辅助开关管导通时间较短,辅助网络存储的能量较少;负载较轻时,D较小,而辅助开关管导通时间增加,存储的能量增加,利于滞后臂实现ZVS。因此,辅助能量与D 密切相关,这与时段2 中分析的情况一致。

图4 简化工作波形Fig.4 Simplified waveforms of proposed converter
从简化波形可以看出,当变换器处于+1(vAB=+Vin) 状 态 与−1(vAB=−Vin) 状 态 之 间 的0(vAB=0)工作状态时,对应Q5导通,辅助电感储存实现滞后臂ZVS 的能量,变换器处于−1 状态与+1状态之间的0 工作状态对应Q6导通,辅助网络储能。基于以上分析的规律,Q5、Q6的门极信号可表示为
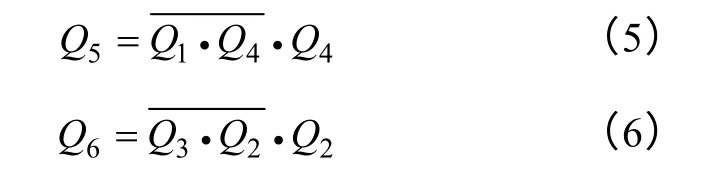
因此,基于对Q5、Q6的控制,这里不再需要额外引入辅助变压器及辅助电容,而仅对主功率管的控制信号进行简单的逻辑运算就可以得到,原主电路拓扑得到明显的简化,如图5 所示。
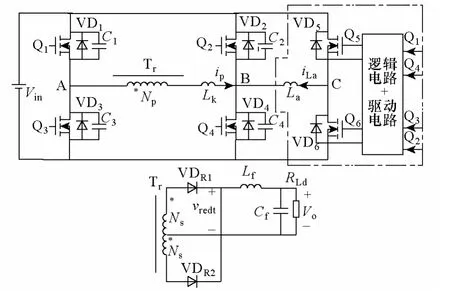
图5 简化后的主电路拓扑Fig.5 Simplified main circuit topology
4 参数设计
前面已经讨论了D≥0.5 时,辅助能量变化规律。需要注意的是,随着负载电流不断地减小,当D<0.5 时,根据伏秒平衡原理,辅助电感的实际储能时间将不变,保持为Ts/4,即辅助网络存储能量不再变化。在全负载范围内辅助电感电流幅值与占空比D 的关系可表示如下:
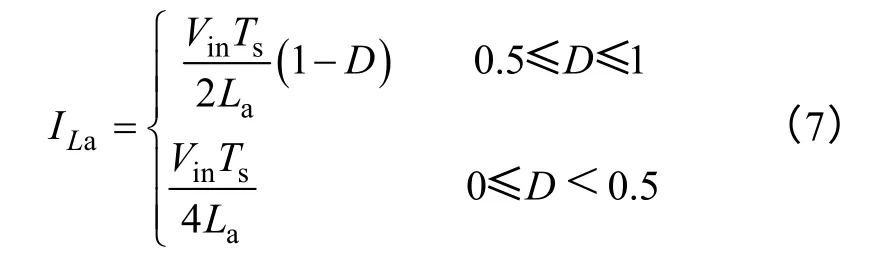
因此,这里对式(2)进行补充,见式(8)。

而电路占空比D 与负载电流Io的函数关系又可表示为
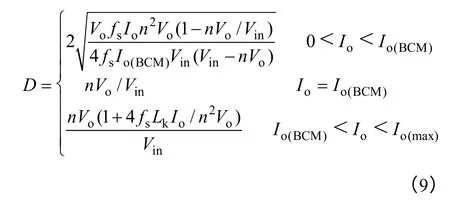
式中,Io(BCM)为输出临界连续电流。
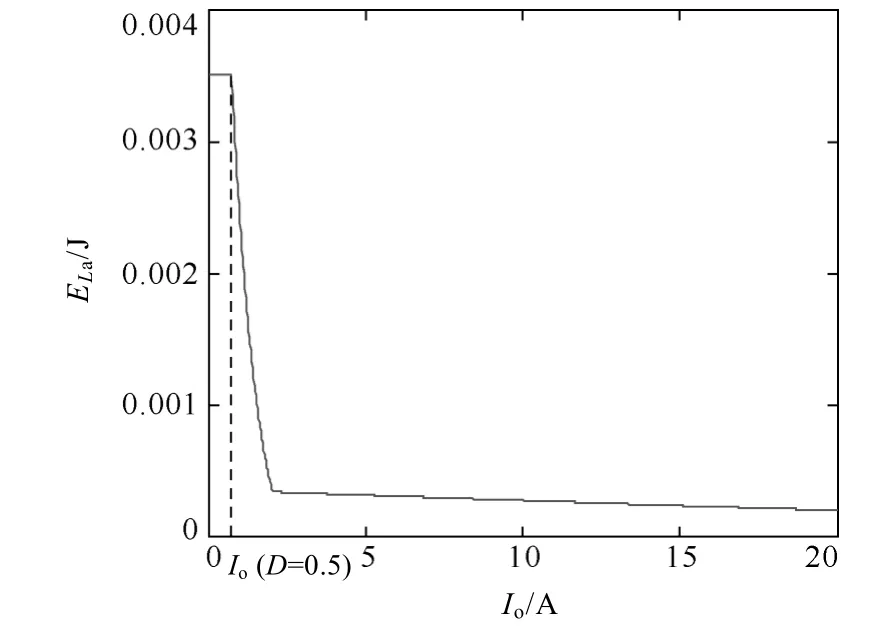
图6 辅助能量ELa与负载电流Io的关系曲线Fig.6 Auxiliary energy ELaversus load current
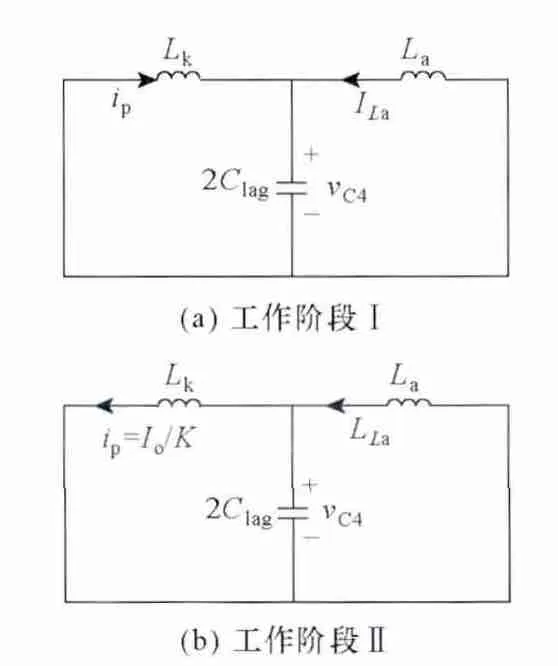
根据式(8)和式(9),图6 给出了辅助能量ELa与负载电流Io的关系曲线。其中,Io(D=0.5)为占空比D=0.5 时对应的负载电流值。可以看出辅助能量在整个负载范围不是恒定不变的。当 Io(D=0.5) 滞后臂暂态过程中,变压器漏感和辅助电感共同作用以实现滞后臂ZVS,暂态过程中辅助电感电流可近似看做恒流源。 倘若将死区时间设定为 td(lag)=Tr/4,其中;同时不考虑一次电流纹波,即一次电流ip=Io/K。 根据负载条件的不同,滞后臂暂态过程可以分为图7 所示的两种情况。在大多数负载条件下,滞后臂只是经历工作阶段Ⅰ,图7a 是其等效电路,一次电流ip谐振下降,滞后桥臂结电容C4电压谐振上升,如果vC4电压能够上升到Vin,即可零电压开通Q2。工作阶段І 中vC4电压变化特征与式(4)表示的一样。 图7 滞后臂暂态过程等效电路Fig.7 Equivalent circuits of lagging-leg transition 实际应用时漏感取值往往较小,导致滞后臂换流谐振周期也非常的短,在某些负载条件下就会出现一次电流迅速下降至折算后的负载电流-Io/K,而滞后桥臂结电容电压 vC4却未被充电至输入电压Vin,这时变换器就会紧接进入工作阶段Ⅱ,如图7b所示的等效电路。工作阶段Ⅱ中辅助电感电流不仅需要提供给滞后桥臂结电容充电的电流,而且同时需要补偿负载电流。 由以上分析的结果来看,滞后桥臂结电容电压vC4在工作阶段Ⅱ中可以表示为 基于以上分析可以画出滞后臂暂态过程中,在不同辅助电感取值下vC4随负载电流变化曲线,如图8a 所示。从图中可以看出,相同的漏感取值下,辅助电感值取得越小,vC4就越容易上升到输入电压Vin,滞后臂实现ZVS 越容易。同时还可看出,滞后臂并不是在空载或临界导通模式(Boundary Conduction Mode,BCM)下最难实现ZVS,而是在连续导通模式(Continuous Conduction Mode,CCM)下某个特定的负载条件。因此,前面分析到当0 图8b 给出了一组不同漏感Lk取值下vC4与负载电流变化的关系曲线。同样可从图中看出,滞后臂并不是在空载或临界连续电流时最难实现ZVS,同样是在某个特定的负载条件。并且在相同的辅助电感取值下,变压器漏感值取得越大,vC4越容易上升到输入电压Vin,滞后臂就越容易实现ZVS。 图8 滞后桥臂结电容电压与负载电流关系Fig.8 Voltage across the parasitic capacitor of lagging-leg versus load current 辅助电感的选取与负载电流及变压器漏感有着密切的联系。为了减小占空比损失及二次整流电压寄生振荡,希望漏感设计的越小越好。但基于以上分析,漏感Lk越小,需要的辅助能量越大,引入的导通损耗也越大,因此这里需要折衷考虑。 4.2.1 辅助开关管选择 辅助开关管的电压应力与主功率管相同,均为输入电压Vin。 辅助电感值确定后,可根据式(7)计算出辅助电感电流的最大幅值。 此时可计算出辅助电感最大电流有效值ILa(RMS) 根据辅助开关管的电压电流定额,即可选取合适的辅助开关管。 4.2.2 辅助开关管软开关分析 辅助开关管零电压开关的条件与电路工作占空比D,即与负载电流大小紧密相关。 当占空比D>0.5 时,如图4 所示。Q5、Q6导通之前,辅助电感电流为零。在辅助电感的缓冲下,此时辅助开关管Q5、Q6近似零电流导通。另外,由于辅助开关管Q5、Q6寄生电容的缓冲作用,辅助开关管可以实现近似零电压软关断。 当占空比D<0.5 时,辅助电流幅值不再增加,波形变为双极性的三角波。通过仿真发现,在 Q5导通前,由于辅助电感电流为负,其反并联的二极管VD5导通续流,Q5两端电压被钳位于零,Q5可实现零电压导通,且这一现象随着D 的减小而愈发明显。同样的,辅助开关管Q6在D<0.5 的条件下,也满足零电压导通条件。 为了验证该新型变换器的工作特性,在实验室搭建了一台1kW/54V 的原理样机,原理样机采用了TI 公司的UCC3895 控制芯片,并采用传统的移相控制策略。实验参数如下:输入直流电压Vin=300~400V;输出直流电压Vo=54V;Q1~Q4为IRFP460;辅助开关管Q5~Q6为IRFP17N50L;输出整流二极管VDR1和VDR2为MUR3040;变压器匝比K 为14:3:3(EE50,TDK-PC40,Ae=226mm2,Aw=252mm2);Lk=7µH;辅助电感La=80µH(EE33,TDK-PC40,Ae=111mm2,Aw=131mm2);滤 波 电 感 Lf=27µH(EE42,TDK-PC40,Ae=182mm2,Aw=260mm2);滤波电容Cf=560µF×4;开关频率为100kHz。 图9 不同负载条件下的vAB与iLa波形Fig.9 vABand iLaat different load 图9 为Vin=350V,输出不同负载时vAB与iLa的实验波形。可以看出,随着负载电流的减小,变换器占空比D 逐渐地减小,而用于辅助电感储能的时间增加。辅助电感电流峰值ILa逐渐增加,辅助电流是随负载变化自适应调整的,提高了变换器性能。 图10 为不同负载条件下滞后臂开关管Q4漏源电压vDS(Q4)和栅源电压vGS(Q4)的实验波形。从各波形中可以看出,辅助网络的加入实现了滞后臂在全负载范围的ZVS。 图10 不同负载条件下滞后管Q4的ZVS 波形Fig.10 ZVS waveforms of lagging-leg switch Q4at different load 图11 为满载条件下vAB、ip和vrect的实验波形。辅助网络的加入使得变压器漏感可以取的较小,因此二次整流电压寄生振荡得到抑制,且几乎不存在二次占空比的损失。 图11 满载条件下的vAB、ip和vrect波形Fig.11 vAB,ipand vrectat full load 图12 将本文提出的变换器与传统全桥变换器的整机效率进行了对比。其中Po为输出功率,η 为效率。轻载条件下,新型变换器效率要高于传统的全桥变换器,这是因为有源辅助网络的引入使得新型变换器更容易实现一次开关管的ZVS。而随着负载的增大,有源辅助网络的优势没有得到明显的体现,从而两种变换器在重载条件下的效率相当。 图12 整机变换效率Fig.12 Conversion efficiency 本文提出了一种辅助电流自调整的移相全桥ZVS 变换器。加入的有源辅助网络拓展了变换器的软开关范围,基于辅助开关管的简单控制,辅助电感电流可随负载电流自调整,减小了导通损耗;由于一次漏感取值较小,二次占空比损失及整流电压寄生振荡得到有效抑制。本文详细分析了该变换器的工作原理、拓扑简化和参数设计,并通过实验验证了该变换器具有的优点及其特性。该变换器特别适用于负载变化范围较宽的中大功率应用场合。 [1]Sabaté J A,Vlatkovic V,Ridley R B.Design considerations for high-voltage high-power fullbridge zero-voltage-switching PWM converter[C].Proceedings of IEEE Applied Power Electronics Conference,1990:275-284. [2]Mweene L H,Wright C A,Schlecht M F.A 1 kW 500 kHz frontend converter for a distributed power supply system[J].IEEE Transactions on Power Electronics,1991,6(3):398-407. [3]陈仲,陈淼,季锋,等.一种采用新型无源辅助网络的 ZVS 全桥变换器[J].电工技术学报,2012,27(11):146-152.Chen Zhong,Chen Miao,Ji Feng,et al.A novel ZVS full-bridge ZVS converter with auxiliary network[J].Transactions of China Electrotechnical Society,2012,27(11):146-152. [4]吴新科,赵荣祥,钱照明.倍流输出电流型输入ZVS 全桥变流器磁集成方案[J].电工技术学报,2008,23(9):80-85.Wu Xinke,Zhao Rongxiang,Qian Zhaoming.Magnetic integration scheme for current fed ZVS full bridge converter with current doubler rectifier [J].Transactions of China Electrotechnical Society,2008,23(9):80-85. [5]陈仲,张鑫,季飚,等.一种基于变压器串联和新型辅助网络的ZVS 移相全桥变换器[J].电工技术学报,2009,24(12):95-101.Chen Zhong,Zhang Xin,Ji Biao,et al.A ZVS phase-shifted full-bridge converter with seriesconnection of transformer and auxiliary network[J].Transactions of China Electrotechnical Society,2009,24(12):95-101. [6]赵川红,徐德鸿,范海峰,等.PWM 加相移控制的双向 DC/DC 变换器[J].中国电机工程学报,2003,23(10):72-77.Zhao Chuanhong,Xu Dehong,Fan Haifeng,et al.A PWM plus phase-shift control bidirectional DC/DC converter[J].Proceedings of the CSEE,2003,23(10):72-77. [7]杜贵平,黄石生.60kW 级软开关等离子喷涂高效电源研究[J].电工技术学报,2005,20(4):94-97.Du Guiping,Huang Shisheng.Study of 60kW plasma spray power supply with soft-switching technology[J].Transactions of China Electrotechnical Society,2005,20(4):94-97. [8]Hua G,Lee F C,Jovanović M M.An improved full-bridge zero-voltage-switched PWM converter using a saturable inductor[J].IEEE Transactions on Power Electronics,1993,8(4):530-534. [9]Jain P K,Kang W,Soin H,et al.Analysis and design considerations of a load and line independent zero voltage switching full bridge DC/DC converter topology[J].IEEE Transactions on Power Electronics,2002,17(5):649-657. [10]陈仲,季飚,石磊,等.基于π型无源辅助网络的新型ZVS 全桥变换器[J].中国电机工程学报,2010,30(21):21-25.Chen Zhong,Ji Biao,Shi Lei,et al.Novel full bridge converter with π type auxiliary network[J].Proceedings of the CSEE,2010,30(21):21-25. [11]Cho J G,Sabaté J A,Lee F C.Novel full bridge zero-voltage-transition PWM DC/DC converter for high application[C].Proceedings of IEEE Applied Power Electronics Conference,1994:143-149. [12]Zhu Lizhi,Qu Wenlong,Li Fahai.A novel softswitching full-bridge PWM DC-DC converter with auxiliary resonant commutating network[C].Proceedings of IEEE Telecommunications Energy Conference,1996:692-697. [13]张欣,陈武,阮新波.一种辅助电流可控的移相全桥零电压开关PWM 变换器[J].电工技术学报,2010,25(3):81-88.Zhang Xin,Chen Wu,Ruan Xinbo.A novel ZVS PWM phase-shifted full bridge converter with controlled auxiliary circuit[J].Transactions of China Electrotechnical Society,2010,25(3):81-88. [14]Jang Y,Jovanović M M.A new family of full-bridge ZVS converters[J].IEEE Transactions on Power Electronics,2004,19(3):701-708. [15]Jang Y,Jovanović M M.A new PWM ZVS full-bridge converter[J].IEEE Transactions on Power Electronics,2007,22(3):987-993.4.1 辅助电感La设计
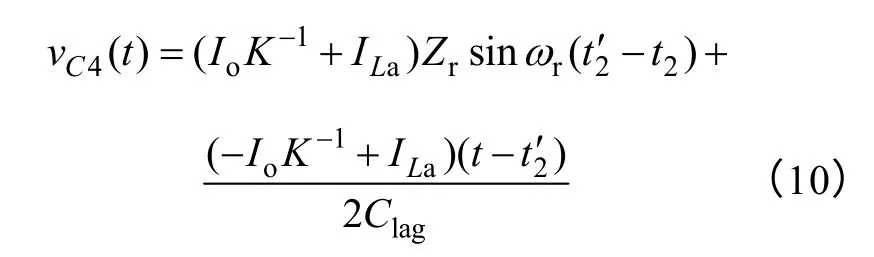


4.2 辅助开关管选择及其软开关分析
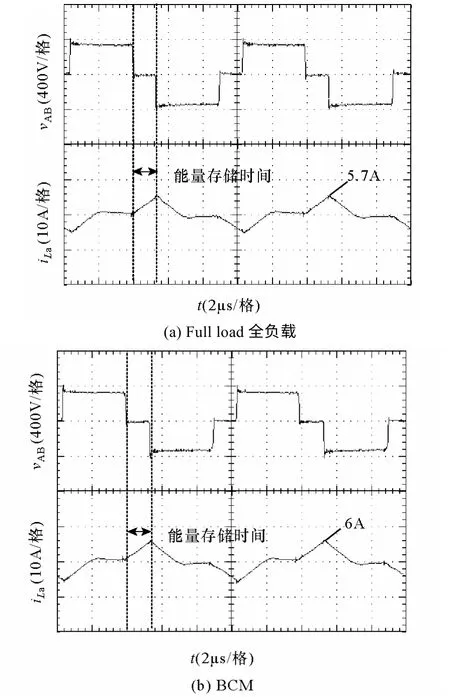
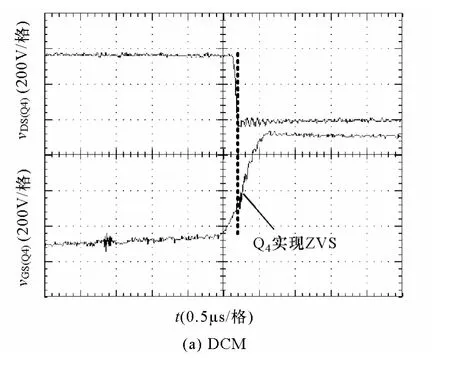
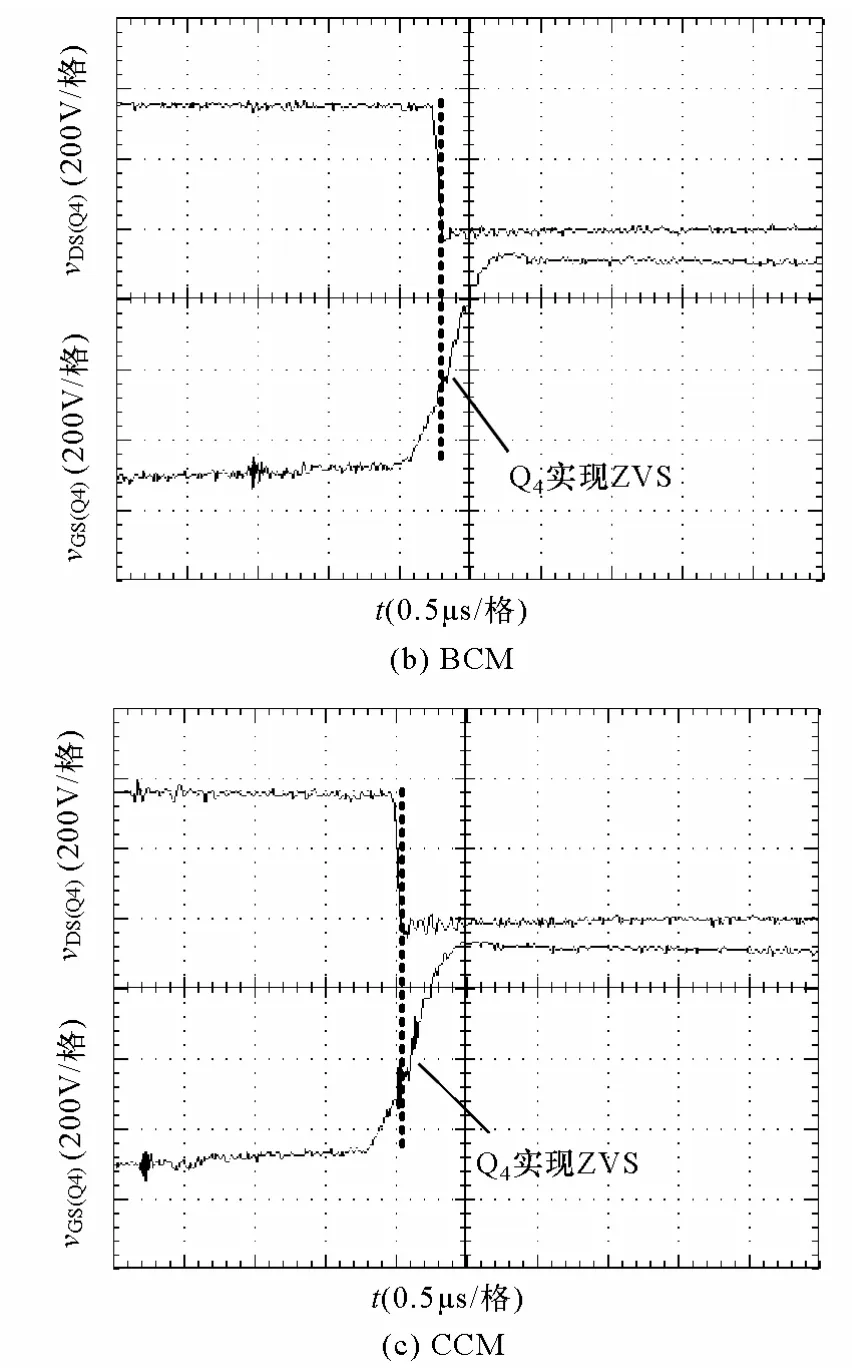
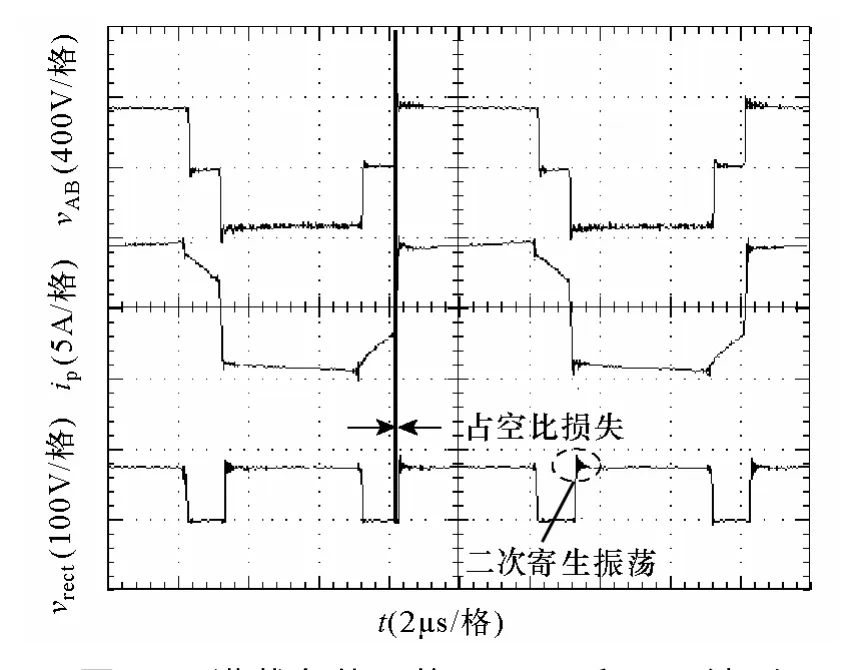
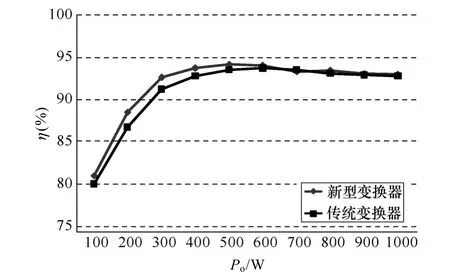
5 实验结果与讨论

6 结论

