艺术类专业教学的质量评价研究——基于AHP层次分析法的模糊综合评判
干羽
江苏省戏剧学校,南京210001
一、引言
教学质量是评估学校是否合格的特别条件,因为学校始终是以提高教学质量为最高目标的。近些年国家将文化产业纳入国民经济和社会发展的整体规划中之后,社会对艺术类人才的需求量不断增大,因此艺术类专业的招生人数逐年递加,例如美术专业从2001年至2010年10年间,招生人数就扩大了10倍[1]。在这样的背景下,如何保证和提高艺术专业的教学质量,就成了亟待解决的问题。
要提高艺术类专业的教学质量,就必须充分认识艺术类专业的特色和教学特点,并建立符合其特点、特色的教学质量评价体系。
艺术类(以美术为例)专业在教学规律方面,除了拥有其他专业的共通性之外,还有自身的特点。例如,它不同于一般文科类专业那样具有写实性,也不同于理工科类专业那样强调理论性、逻辑性,而是注重直观性、形象性和应用性。其教学过程始终围绕着审美个性的形成和空间造型能力的提升这几个目标。同时,由于教学内容的多样化和学生的不同个性,课堂具有灵活性、自由性等特点。教师在教学时并非单一地讲授,而是有演示也有传帮带,三者紧密结合。要在课堂中花费大量时间培养学生的综合素质,提高创作能力和专业表现能力,因此作业也是以技巧训练为主的[2]。
目前很多艺术院校对教师的教学评价依然采用传统的、以定性分析为主的方法。实践证明,这样的方法片面、主观,也不适用于所有专业的评估。有基如此,本文以艺术类专业为对象,经过反复调查、研究与比对,试图建立一套科学的且符合专业特征的课堂教学质量评价指标体系。
美国学者T.L.Saaty在20世纪70年代提出了一种较为复杂的分层次的权重解析法——层次分析法(AHPAnalytic Hierarchy Process——AHP)。这种评估方法的层次细致,适用于多目标、多准则问题的决策。AHP结合各种因素确定权重,不仅定性分析而且能够定量分析,所以比较客观、科学。尤其是能够方便处理那些结构复杂、原则过多也不太容易量化的系统问题,所以有较强的适应性[3][4]。
艺术类专业教学质量评估要面对各种复杂、特殊的因素,如果使用AHP方法就完全可以顺利解决教学质量各项评价指标的权重问题。
应该指出,教师教学质量等级的确定并没有特别清晰的界限,所以本文特意将模糊综合评判法与AHP相结合,建立了基于AHP的模糊综合评判模型。换言之,就是首先使用层次分析法区分出教学质量评估的各级层次,确定它们之间的关系以及权重,然后运用模糊评判公式计算出相应的结果。
制订评价指标、构建评价体系,必须充分吸取作为学习主体即学生的意见,同时还要认真听取任课教师以及同行专家的意见。为此,笔者做了如下工作:
第一,通过与学校教学质量监控部门以及教师、同行专家的沟通、研究与探讨,综合成了五项“一级评价指标”,即“教学态度、教学内容、教学方法、教学水平和教学效果”[2]。
第二,选取六个不同班级,在班主任的配合下,发放了190份调查问卷。每个被调查的学生以匿名方式在问卷上填写自己对上述“一级指标”中每个项目的看法并按轻重情况排序。
第三,笔者向21位任课教师和同行专家发放了与学生一模一样的问卷。
通过统计、分析和研究,得出了一份比较合理的、能确定各项指标高低程度的表格,为下一步的层次分析法所运用的“判断矩阵”奠定了基础。
二、建立科学的教学质量评价指标体系
建立科学、合理、切实可行的教学质量评价指标体系,就是为了准确评价课堂教学质量,并能真正了解教与学的效果[5]。
如前所述,通过调查和探讨,笔者提炼出了五项对课堂教学质量有着重要影响的“一级评价指标”(见表1)[6][7]。然后,赋予每项一级指标以详细的内涵,于是形成了“二级评价指标”。
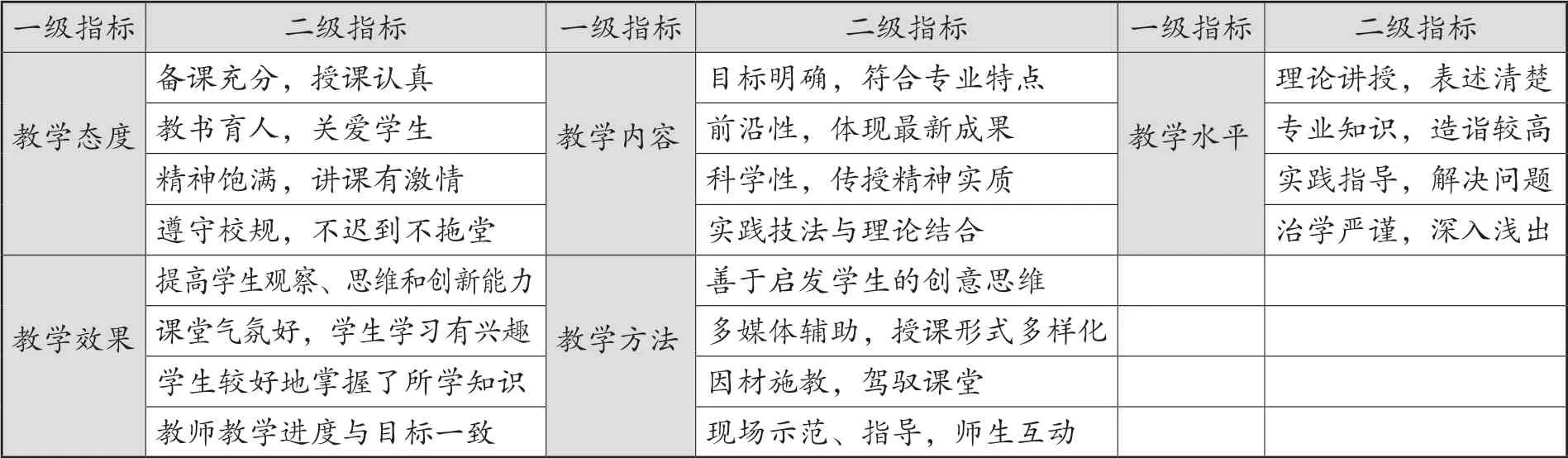
表1 课堂教学评价指标
三、构建模糊综合评判及AHP模型
两个评价标准的建立,为科学合理地评价课堂教学质量提供了基础与条件。首先是建立课层次结构模型,再将AHP与模糊综合评判法相结合,通过计算得出了综合的评价结果[8][9]。
1.构建评价指标层次结构模型
以上制定的五个一级指标和与之关联的20个二级指标,构建了如图1所示的层次结构模型。
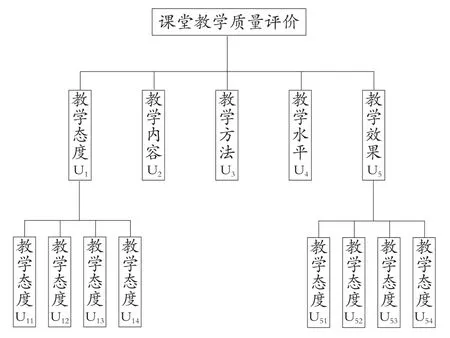
图1 课堂教学质量评价体系层次结构①
对图1的说明:
最上方的一栏属于A目标层,是对课堂教学质量的评价。
中间的一栏属于B主准则层,是由U1~U5五个一级评价指标构成的。
最下边的一栏属于C子准则层,被细分出20个二级评价指标,每1个主准则分别对应与其相关的四个子准则,即U11-U14、U21-U24、U31-U34、U41-U44、U51-U54。
2.应用AHP确定权重集[7]
确定权重集,就是因为它能客观反映各个指标在总体评判中所占的分量和地位。以下是应用AHP算法确定权重的运算过程:
第一,构建判断矩阵A。5个一级评价指标两两比较(见表2),就得到了如下结果(见表3):
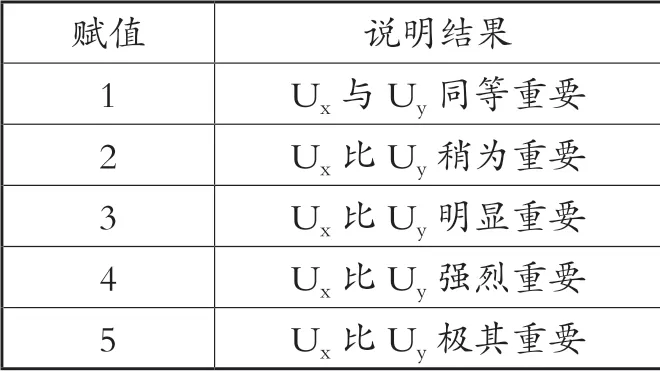
表2 1~9标度法说明(表格自制)
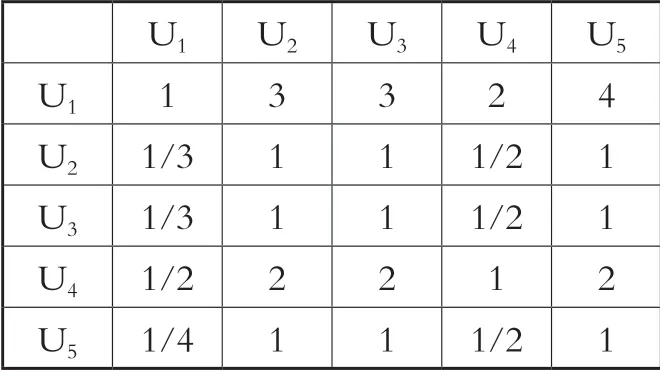
表3 指标集合两两比较的结果
用矩阵表示为:
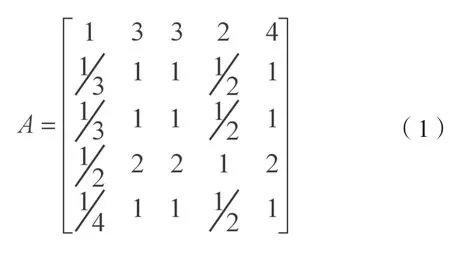
第二,求出权重集。
对A 按列归一化:


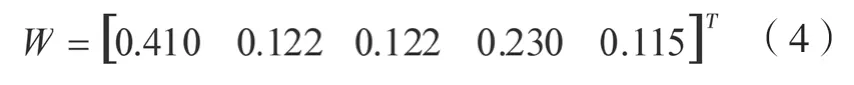
第三,判断矩阵的一致性检验:

而
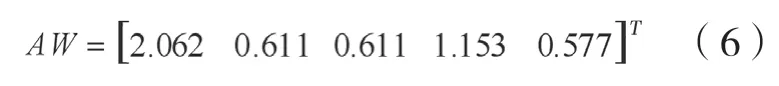
将(6)式代入(5)式 得
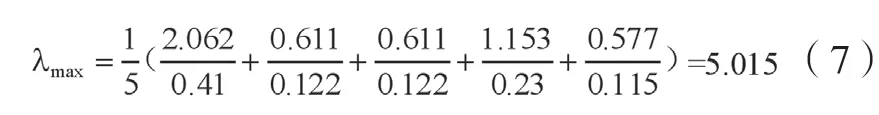
一致性指标
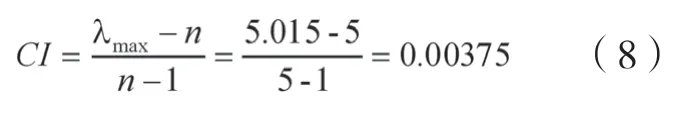
根据表2、表3可知n=5时,一致性指标为RⅠ=1.12,得出检验矩阵的一致性为:
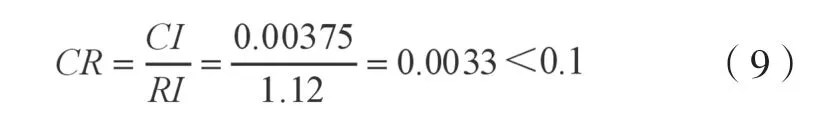
由此结论:以上计算出来的权重集可靠、合理。
用相同方法,可以求出二级指标的权重集(其过程省略),结果如表4所示:
3.教学质量的模糊综合评判
模糊评判的基本原理就是在确定了评价因素的等级和权重的基础上,运用模糊集合变换原理,以隶属度描述各因素的模糊界限,构造模糊评判矩阵,通过多层复合运算,最终确定评价对象的等级[9][6]。
(1)构建评判集:V
所谓“评判集”就是对各层指标的语言性描述,即评价者对各个评价指标给出的评语。可以简单举例:人们对教学质量通常会按四个等级给出评语,因此这个评判集为:
V={ V1,V2,V3, V4,}={优,良,中,差}
(2)建立模糊评判矩阵:R
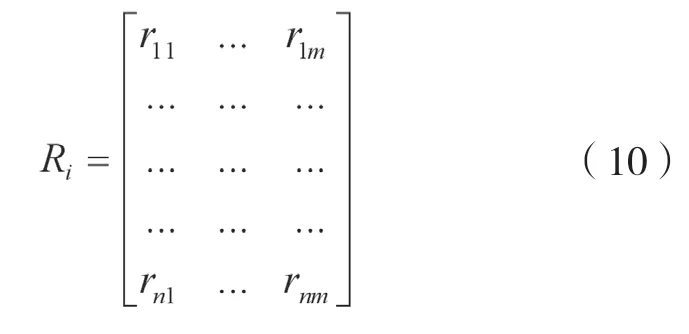
(i=1,2,… ,5; n=4; m=4)其中rij表示因素ui对评语等级vj的隶属度。
(3)模糊评判的综合算法
在从低层向高层逐层的计算中,采用的是模糊数学的M(·,+)模型。该模型不仅考虑了所有因素的影响,而且保留了单因素评判的全部信息。[9]
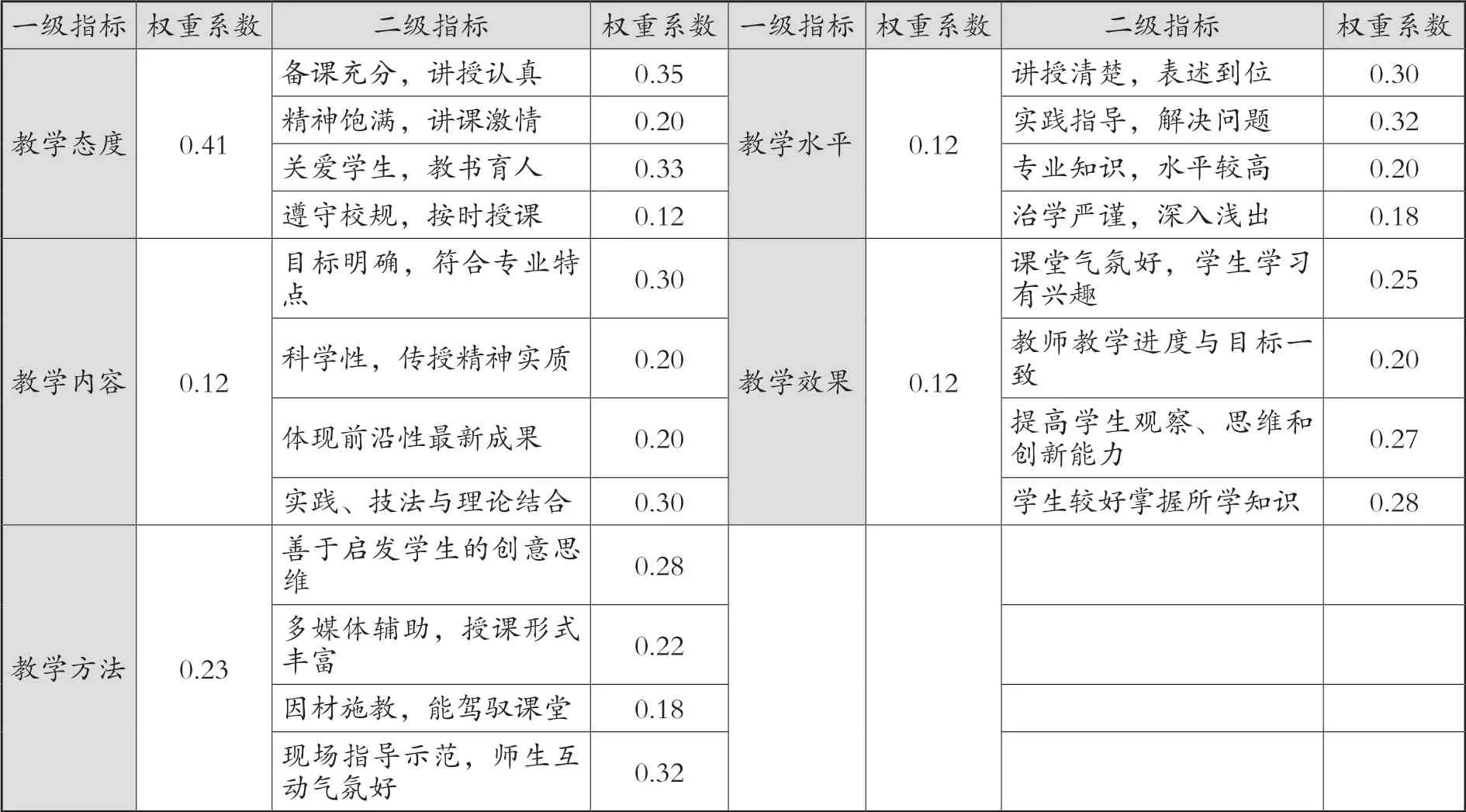
表4 课堂教学质量评价指标权重体系[7]
一级指标单因素评价矩阵为:
B1=A1·R1 B2=A2·R2 B3=A3·R3 B4=A4·R4 B5=A5·R5
式中A1~A5分别为各一级指标所属的二级指标的权重集。
最终结果的评价矩阵是:
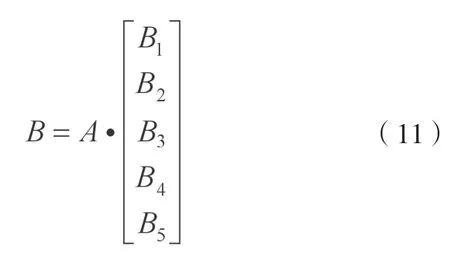
式中A为一级指标的权重集。
最后,根据最大隶属度原则,得出评价等级。
四、应用实例
对教师甲的授课,笔者收集了10位同行专家的评价表,结果如表5所示[7]。得出结论之前,先将课堂教学质量分为优、良、中、差4个等级。
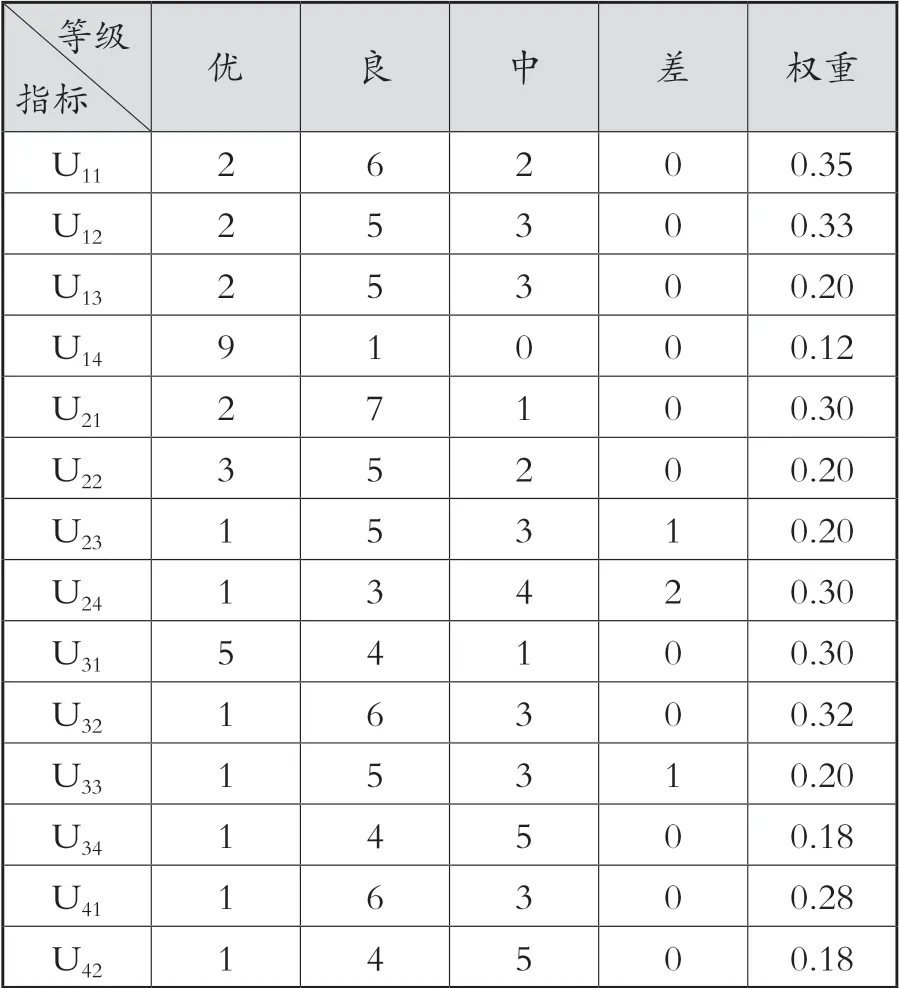
表5 课堂教学评价统计(表格自制)
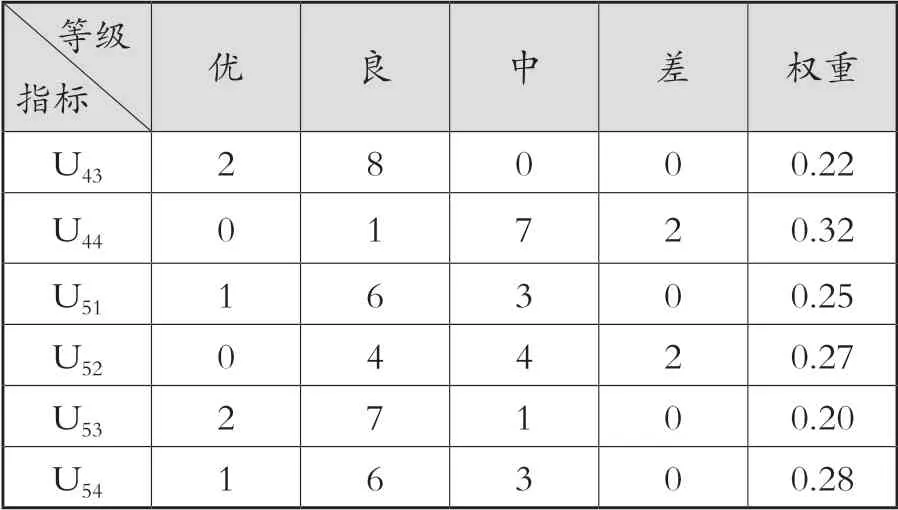
等级指标 优 良 中 差 权重U43 2 8 0 0 0.22 U44 0 1 7 2 0.32 U51 1 6 3 0 0.25 U52 0 4 4 2 0.27 U53 2 7 1 0 0.20 U54 1 6 3 0 0.28
1.建立评判集V
V={V1, V2, V3, V4,}={优,良,中,差}
2.建立模糊评价矩阵
根据以上统计结果,建立一级指标的模糊评价矩阵——R1~R5

3.综合评判
作各个一级指标的综合评判计算。
B1=A1·R1
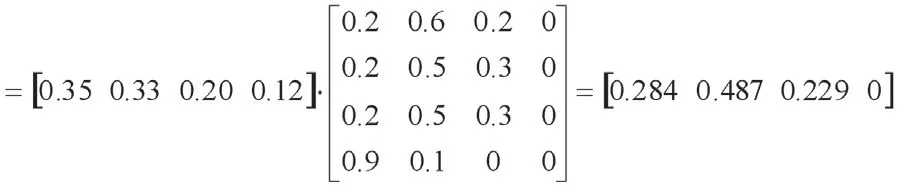
B2=A2·R2

B3=A3·R3

B4=A4·R5

B5=A5·R5

因为一级指标的权重集为:
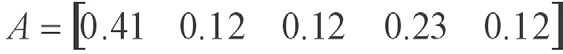
所以最终综合评价的结果是:

上述结果表明,该教师教学质量属于“优”、“良”、“中”、“差”的隶属度分别为0.194、0.496、0.283和0.027。根据最优原则,这位教师的课堂教学质量评价为“良”。如果按分数计算,可取“优=95,良=85,中=75,差=60”,则:

4.验证
为了验证本评判法的客观性,可以选取教师乙为对象。对其授课,同样收集了同行专家的评价表,结果如表6所示。
表6 教师乙课堂教学评价统计(表格自制)
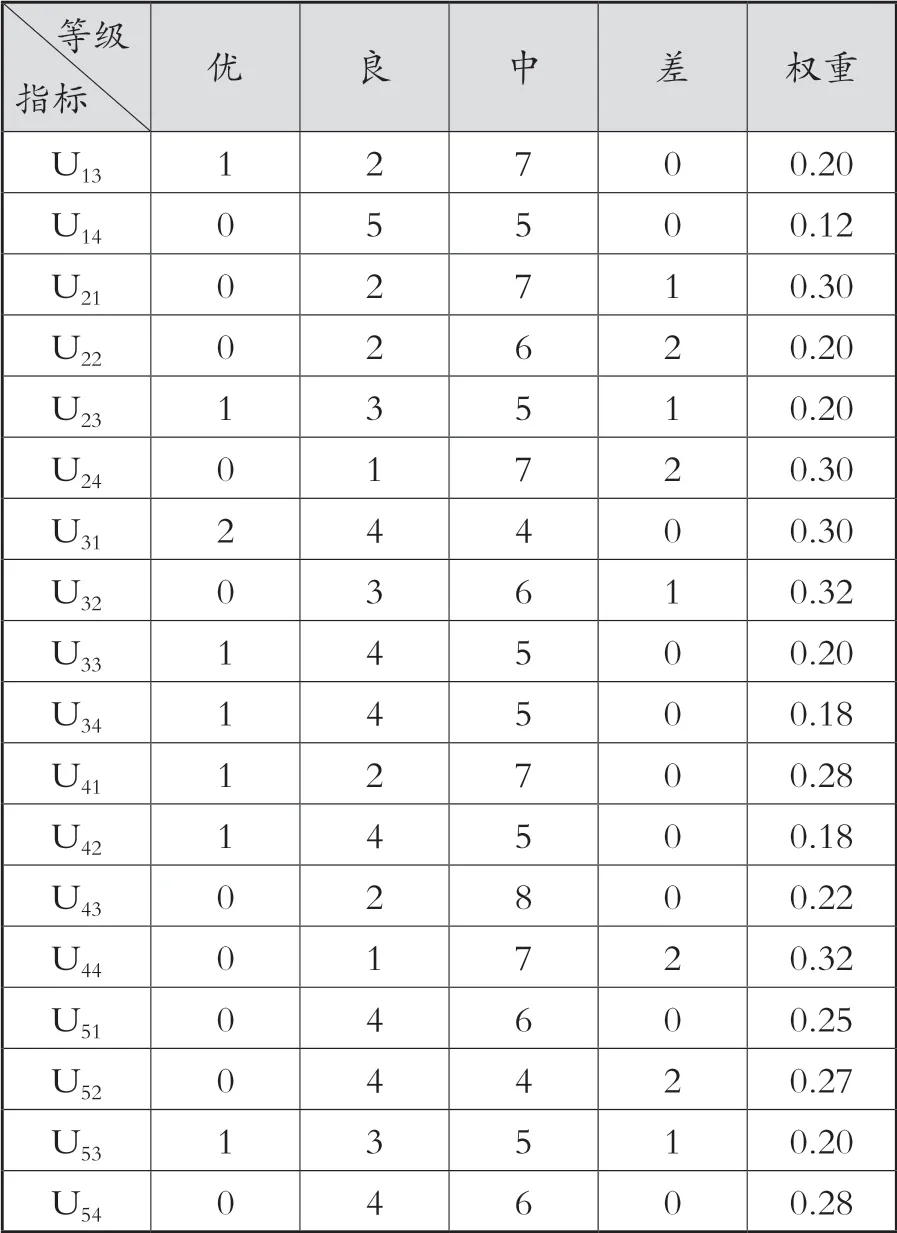
等级指标 优 良 中 差 权重U13 1 2 7 0 0.20 U14 0 5 5 0 0.12 U21 0 2 7 1 0.30 U22 0 2 6 2 0.20 U23 1 3 5 1 0.20 U24 0 1 7 2 0.30 U31 2 4 4 0 0.30 U32 0 3 6 1 0.32 U33 1 4 5 0 0.20 U34 1 4 5 0 0.18 U41 1 2 7 0 0.28 U42 1 4 5 0 0.18 U43 0 2 8 0 0.22 U44 0 1 7 2 0.32 U51 0 4 6 0 0.25 U52 0 4 4 2 0.27 U53 1 3 5 1 0.20 U54 0 4 6 0 0.28
中间计算过程类似,此不赘述。而最终的评价结果是:

上述结果表明,该教师教学质量属于“优”、“良”、“中”、“差”的隶属度分别为0.063、0.298、0.594和0.045。根据最优原则,这位教师的课堂教学质量评价为“中”。如果按分数计算,可得:

五、结语
本文针对艺术类专业课堂教学的特点,建立了科学、客观、合理的课堂教学综合评价指标体系。
对于制定的指标(五个一级指标和20个二级指标),笔者运用的方法是:先利用AHP层次分析法确定各评价指标间的权重,再与模糊数学综合评判模型相结合。用这种全面的方法来评判(评价)艺术类教师的教学质量,更严谨,更科学也更符合实际,本文列举教师甲和教师乙的例子就具极大的说服力。
由于本方法涉及较为繁琐的矩阵运算,可以充分利用网络,建立“基于网络的教学质量评价系统”,以解决复杂的计算问题。同样的,这种系统也是可以实现网上评教和分级查询的:学校的教学职能部门能够随时了解全校的教学情况,便于监控;教学单位也可以随时查询,了解本单位教师获得的评价。最重要的是,每位教师可以通过网络,及时了解学生对自己的评估和评价,扬其长而弃其短。
注释
① 图中U2、U3和U4所对应的U21-U24 、U31-U34 和U41-U44因篇幅受限,特意省略.
[1]郑泓灏.高校美术专业的教学质量评价探析[J].高教探索,2013(3):1-7.
[2]刘红.探讨模糊综合评判法在艺术院校教学质量评价中的应用[J].科技信息:学术研究,2008(9):295-296.
[3]许树柏.实用决策方法——层次分析法原理[M].天津.天津大学出版社,1988:14-23.
[4]林齐宁.决策分析[M].北京.北京邮电大学出版社,2002:102-113.
[5]范恺洋.课堂教学质量评价体系的构建与实践[D].上海:第二军医大学,2005:19-30.
[6]王国胜.河流健康评价指标体系与AHP——模糊综合评判模型研究[D].广州:广东工业大学,2007:39-40,42.
[7]干敏梁,干羽.基于AHP和模糊综合评判法的课堂教学质量评价研究[J].三江高教,2013(03):1-7.
[8]尹亮亮,苏兴.高校教师教学质量评估体系研究——基于AHP的模糊综合评价方法应用[J].合作经济与科技,2012(3):92-94.
[9]尹爱芹,李云.模糊综合评判在教学质量评价中的应用研究[J].泰山学院学报,2010(3):18-20.
[10]王淼.天津市道路客运枢纽总体布局规划研究[D].天津:河北工业大学,2006:41-45.

