培养学生观察能力的点滴体会

严云霞

通过8道数学例题来论证中学数学教学中，学生观察能力培养的重要性，在激发学生兴趣的同时，教师需要通过多种观察问题的方法，选择适当的观察角度，有助于能提高学生的观察能力。

中学数学学生观察能力兴趣培养著名数学教育家玻利亚认为：最好的学习方法是通过自己的发现学习知识。而发现的基础即是观察。要解决一个问题，首先要认识这个问题，所以，解决问题的第一步就是要善于观察。只有细致的观察，才可能发现事物细微而重要的特征差异，捕捉到对解决问题有用的信息，从而找到解决问题的突破口。所以在数学教学中应结合教学内容，着力培养学生的观察能力。下面谈谈自己的一些看法和体会。

一、培养学生观察问题的兴趣

并不是每一个学生都对观察问题有兴趣，要观察一个问题，必须对这个问题有好奇心，有“想看一看”的念头，不然，即使面对一个现成的数学规律也会觉得平淡无奇而对它熟视无睹。在初中数学教学中笔者曾采用下述例1、例2的方法，来培养学生的兴趣。

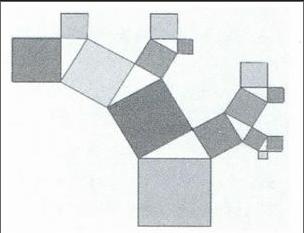
例1：在初一新教材第一章《生活中的平面图形中》中，某教师给出一棵“毕达哥拉斯树”（图1），提问学生：这是一棵不断生长的“毕达哥拉斯树”，请同学们观察，它是由一些什么图形构成的？学生回答：是由正方形和直角三角形构成的。教师再问：“那么它们是怎样构成图形的？有什么规律吗？”

接下来鼓励学生作进一步的观察并且互相交流。学生回答：以正方形的边长作为直角三角形的最长边，在正方形外作直角三角形，再分别以直角三角形的其他两边为边长在直角三角形外作正方形，如此循环往复得到的。

二、培养学生观察问题的方法

只有兴趣，是不能很好观察问题的。如果没有恰当的观察问题的方法，往往事倍而功半。观察一般同比较方法相结合，应注意以下两点：

1.观察问题的相同之处

一个问题总是由几个部分组成的，各部分之间会有相同之处，甚至几个问题之间也有相同之处，他们或者具有相同的形式，或者属于同类知识，或者解题时要用到相同的方法。这些相同之处就是问题的特点。根据这些特点，就可以发现问题的内在联系和本质规律，找到解决问题的突破口。

例2：在初二几何中，结论“三角形的中线将三角形分成等积的两部分”。

由这个结论出发，让学生观察可以发现对于△ABM和△ACM分别以BM、CM为底边时，它们等高，则面积的大小关系取决于BM、CM的大小关系。这时，教师又向学生提出这样的问题，如何由顶点A出发引出一线段AK将原来的△ABC的面积分成具有指定的比例值（如3：2）两个三角形？那么任何比例呢？

如果学生理解了上述的结论，这时自然也就容易找出以下的做法。由此，一道学生们认为比较复杂的问题就被解决了，使学生享受到成功的喜悦。

例3：已知，PA是圆O的一条割线，与圆O相交于点B，圆的半径是r，PO=d，用r、d的代数式来表示PA·PB·

拿到这道题，很多同学都陷入沉思。这时我在黑板上进行演示，我把AB绕P点旋转，且分别在CD处、EF处停留一会儿，让学生慢慢地领悟到AB转到CD或EF，PA·PB或PC·PD或PE·PF的值不变。

此时，学生充分联想到PA·PB是一个定值，那么如何把PA·PB转化为r与d的关系式？由AB的位置变化而PA·PB的值不变这一特征联想到：将AB旋转到过圆心O，就可得到r与d的关系。

学生：将AB旋转到特殊位置上：经过圆心OPA·PB=PC·PD=（d+r）（d-r）= d2-r2

变式：如果AB是圆O的一条弦，上述结论有何变化？

当点P在圆内时，PA·PB=PC·PD=（d+r）（d-r）= d2-r2

这一深入研究，学生通过观察，把一般情形转化为特殊问题、化动为静的思想方法，用运动的观点去探索图形变化过程中的内在规律。

2.观察问题的不同之处

正如“世界上没有完全相同的两片树叶”，任何一个问题都有不同之处，如果是本质上的不同即使很微小，都可能由此产生不同的效果。

例4：为了及时巩固学生对等腰三角形性质的理解，我设计了这样一组练习题：

A.如果等腰三角形一个底角是75°，那么它的顶角是多少度？

B.如果等腰三角形一个顶角是75°，那么它的底角是多少度？

C.如果等腰三角形一个内角是75°，那么其余两个角是多少度？

D.如果等腰三角形一个内角是110°，那么其余的角是多少度？

要求学生仔细观察，找出问题中的“底角”“顶角”“内角”的不同，从而找出正确的答案。由浅入深，加强学生的理解和运用。

对类似的问题如果不能看到它们的不同之处，就会盲目套用相同的方法求解而出现失误。

例5：当m为何值时，下列方程有两个实根。

（1）x2+（2m+1）x+2=0 （2）（m-1）x2+（2m+1）x-（m-1）=0

解：（1）b2-4ac=（2m+1）2-4（m-2）=4m-7≧0

解得：m≥4/7

（2）b-4ab=（2m+1）2-4（m-1）（m+1）=4m+5≧0

解得：m≥-5/4

同一类问题，同学用判别式求解（1）的解法正确。（2）的解答错误，两个问题的不同之处在于二次项系数，在（2）中还应考虑二次项的系数不为0。

同样在教学中，对于一道习题不就题论题，而进行适当的引申和变化，逐步延续伸展，让学生随问题变化而变化，观察随着条件或结论的变化而引起整体问题的变化。在培养学生思维的变通性的同时，让学生的思维变得深刻流畅。

三、选择恰当的观察角度

对某个问题，当我们从某个角度看不能发现它的特点时，换一个角度，从它的侧面或反面去观察就容易发现它的本质特点，所以观察问题必须选择恰当的角度。

例6：比较1111111与111111111的大小分析：作减法直接通分比较是相当困难的，“正难则反”，换一个角度去观察，取倒数，则比较容易。

解：∵ 1111111 =10 1111 111111111=10 11111

显然101111>10 11111，即1111111﹥111111111

∴1111111﹤111111111

另外，对于某些问题，我们通过数或形的特征分析，知道这个问题属于什么类型，我们就可以用以前储备的经验去解决它。

例7：已知a-b= -2， a-c= -1

求（c-b）[（a-b）2+（a-b）（a-c）+（a-c）2]的值

仔细观察题目，我们可以发现中括号内的代数式形如x2+xy+y2的形式，这很容易联想到公式（x-y）（x2+xy+y2）=x3-y3。于是凭直觉也能感到，这是一个用立方差公式化简求值的问题，剩下的问题就是由已知条件去得到x-y=c-b，显然（a-b）-（a-c）=c-b。

通过以上例题的分析，说明在中学数学教学过程中，尤其是课堂教学过程中，需要注重培养学生观察能力。当然，良好的观察能力不是一朝一夕所能成功的，必须通过教师坚持不懈的努力，让学生在学习中发挥主观能动性，并持之以恒必然能取得好的教学效果。endprint