基于直流概率潮流的风电穿透功率极限计算

张文婷，范立新

(1.东南大学电气工程学院，江苏南京 210096；2.江苏方天电力技术有限公司，江苏南京 211102)

近年来，随着国家对风能等清洁能源的高度重视，风力发电市场不断扩大，风电装机容量大幅增加。风电的波动特性是影响电力系统对其接纳能力的最大因素[1]。为了能在保证系统安全运行的情况下尽可能地利用风能，则必须求解出风电场能够接入某一电力系统的最大容量。

风电穿透功率极限是指系统能够接受的最大风电场装机容量占系统最大负荷的百分比[2]。由于风电场的接入对电力系统会产生多种影响，所以风电穿透功率极限的求解没有统一的办法。在求解风电穿透功率极限的过程中，需要获取系统中的线路潮流分布情况。由于在系统规划设计阶段，原始数据并不很精确且规划方案众多，对于计算速度的要求比精确度更高，因此产生的直流潮流可以在合理的误差内大大提高计算速度。概率潮流计算方法可计及电力系统运行的各种扰动和随机因素，快速得到支路潮流的概率描述。在其几种主要的求解方法中，蒙特卡罗随机模拟法算法简单，但是运算量大，耗时较长，文献[3]指出传统的蒙特卡洛模拟忽略了系统的稳态运行。卷积法在处理大规模的电力系统时，计算繁琐。半不变量法是卷积法的一种简化算法。文献[4]利用了半不变量法计算得到了接入大规模风电设备的电力系统中线路的概率潮流分布，结果表明与蒙特卡洛模拟法相比，这种方法在保证正确率的同时，大幅减少了计算的时间。

1 直流概率潮流计算方法

1.1 理论基础

设随机变量x的概率密度函数是f（x），期待值为μ，可以求出其v 阶原点矩和中心矩：

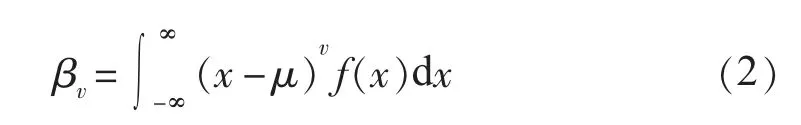
半不变量Kv是随机变量的一种数学特征，它可以由不高于相应阶次的各阶矩求得[5]。为了简化级数形式，定义gv：

式（3）中：gv为v 阶规格化半不变量；σ为标准方差。

利用规格化后的各阶半不变量gv，可以把随机变量x的分布函数表示为以下形式的Gram-Charlier 级数展开式：

式（4）中：f（x）为随机变量x 取值大于或者等于的概率；N（x）为标准正态密度函数；Nγ（x）为Hermite 多项式，这里用到的是规格化随机变量。

1.2 直流概率潮流模型

直流潮流算法关心的是电网有功潮流分布，仅通过一次解维线性方程组便可得到有功潮流分布。对于大规模长距离电网，基于文献[6]的一系列假设可得节点注入有功功率的计算方程的矩阵形式：

式（5）中：P 和θ 分别为n-1 阶节点有功功率注入和电压相角向量。

在直流概率潮流计算中，可将公式写成一般矩阵的形式：

式（6，7）中：W为节点注入有功功率向量；X为节点相角构成的状态变量；f为功率方程；Z为支路潮流向量；g为支路潮流方程。

当系统的注入功率和支路潮流发生扰动时：

将式（8，9）按泰勒级数展开并忽略高次项，得：

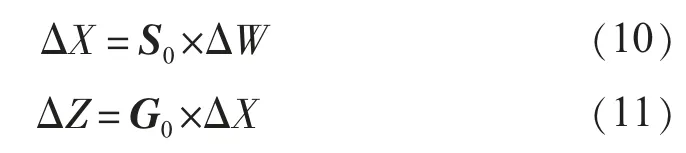
其中：

将式（12）代入式（13）可得：

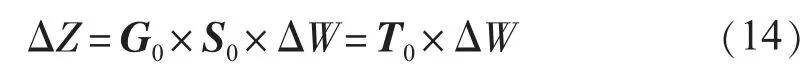
运用半不变量2个重要的性质：（1）随机变量之和的各阶半不变量等于各随机变量的各阶半不变量之和；（2）随机变量a 倍的k 阶半不变量等于其 阶半不变量的ak倍。可以得到状态变量ΔX 和ΔZ 支路潮流的各阶半不变量，即：

这样根据式（4）就可以在已知各节点发电机出力分布、负荷分布的情况下分别得到发电机与负荷的半不变量，然后求解出支路潮流的概率分布。同样地本文将风机视为节点负荷接入系统后，得到含有风电场的电力系统中支路潮流的概率分布。

2 风电穿透功率极限求解模型及算法

2.1 风电场随机出力模型

研究结果验证，大部分地区的年平均风速的概率分布几乎都符合Weibull 分布[7]。Weibull 分布的概率密度函数：

式（17）中：v为风速；k（＞0）为形状参数；c（＞0）为尺度参数。

风力发电机输出功率曲线如图1 所示。它描述的是风力发电机出力与风速之间的关系。

根据图1，风电机输出的有功功率Pw与风速v 之间的函数关系：

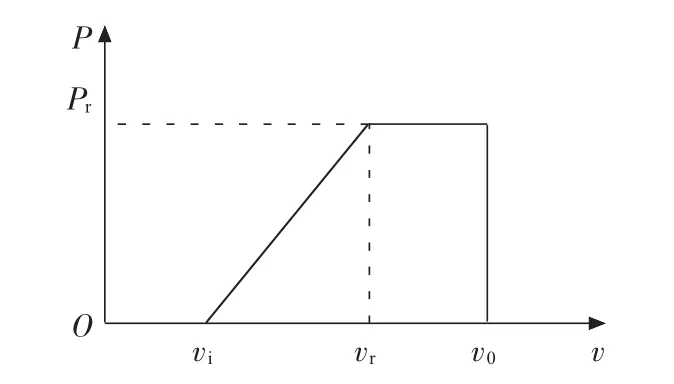
图1 风电机功率输出曲线

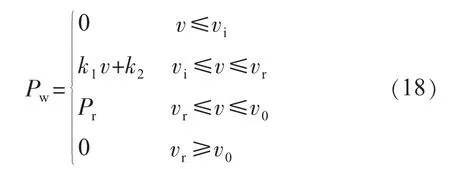
式（18）中：k1=Pr/（vr-vi），k2=-k1vi。其中Pr为风机发电机的额定功率；vr为额定风速；vi为切入风速；v0为切出风速。

经统计，在绝大部分时间内风速维持在vci和vr之间，Pw与v 近似为一次函数关系。在不考虑风电场尾流效应等因素时，风电场的有功出力Pf可以用运行的风机数乘以单台风机的出力求得：

式（19）中：n为运行的风机数；Pw为单台风机的出力。

结合风速的概率密度函数可得风电场输出有功功率的概率密度：

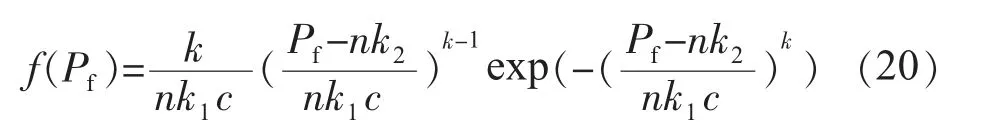
其概率密度分布为三参数的Weibull 分布函数。

2.2 随机规划模型

采用随机规划理论求解基于直流概率潮流的风电穿透功率极限，可将风电场可接入容量的最大化作为目标函数，系统可调参量（如发电机出力）作为控制变量，由控制变量决定的参量（如节点电压相角）为状态变量，直流潮流方程为等式约束，系统安全运行及稳定性水平为不等式约束。考虑到支路传输的有功功率存在一定几率越限，由直流概率潮流求解线路潮流概率分布后，可以得到有功功率越线的概率，其应该小于一个水平。所以给出输电线路输送有功功率上下限和系统频率偏移约束2个不等式约束条件。

2.2.1 目标函数

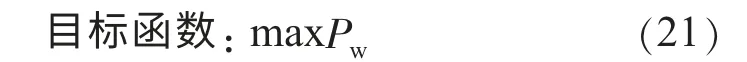
2.2.2 约束条件

（1）输电线路输送有功功率极限约束：

式（22）中：Pij为输电线路传输的有功功率；Pmax为输电线路传输有功功率上限。

（2）系统频率偏移约束：

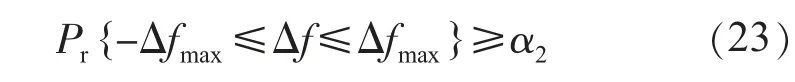
式（23）中：Δf为系统频率偏移；Δfmax为系统频率偏移上限。

频率偏移可通过系统的静态频率特性计算：

式（24）中：ΔP为系统有功功率不平衡量；Ks为系统单位调节功率。Ks包括发电机单位调节功率KG和负荷单位调节功率KL，即：

其中：

2.3 算法流程

随机规划模型的求解采用改进遗传算法[8]。其相较于传统的遗传算法增加了保留操作，即将上一代种群中的若干最优染色体直接复制到本代，为保持种群规模不变，将本代最差的染色体删去。数学上可以证明改进的遗传算法能以概率“1”收敛于全局最优解。

总的来说，采用随机规划和遗传算法求解基于直流概率潮流的风电穿透功率极限计算，就是通过遗传算法产生初代染色体种群，也就是随机产生风电场装机容量的初始种群后，综合考虑风电场出力，发电机出力，负荷功率等的随机性，将各节点注入功率视为相互独立的随机变量，通过直流概率潮流计算得到这些随机变量的概率分布后，检验是否满足设定的约束条件，然后进行交叉、变异、复制、保留操作，产生新的种群，如此反复直到设定的代数。基于直流概率潮流的风电穿透功率计算方法求解流程如图2 所示。

图2 基于直流概率潮流的风电穿透功率极限计算流程图

3 算例

本文采用IEEE 30 节点网络作为测试系统，计算其接入风机后的有功潮流概率分布，以分析风电场对电力系统的影响，求解风电穿透功率极限。IEEE 30 系统有30个节点，41 条支路。其接线如图3 所示。

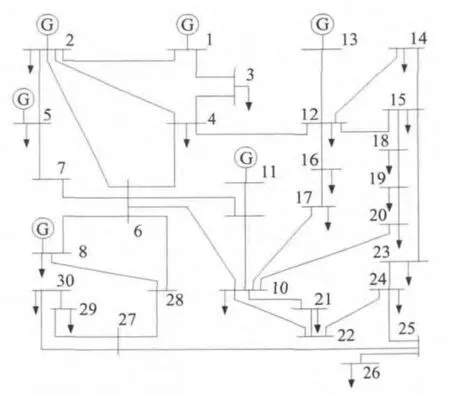
图3 IEEE 30 节点测试系统

表1 不同风机接入容量时典型支路的不过载概率

从表1 可看出，随着风机接入容量的增大，线路有功潮流的稳定性在变差，支路电流的过载概率增大，这会严重影响电网中的电能质量、频率稳定及安全性。此外，由表1 中数据还可看出，支路21-22 和22-24的过载概率最大，而距离节点22 较远的支路2-4的过载概率很小，说明风电场的接入，使得距离风电场接入点越近的支路受到的影响越大。下面给定约束条件，假设风电场有功功率的最大变化率不超过其装机容量的20%。各约束的置信水平取值如表2 所示。

首先选择风电装机容量作为染色体[Pw22]，在[0，0.6]（总负荷大致接近于3）范围内随机产生风电机装机容量，经过300 代的计算后，染色体逐渐收敛于最优解。最终生成的染色体为[0.232 3]，代入校验函数得到表3。

表2 各约束条件的置信水平

表3 越限概率校验

其置信水平符合要求，即为最优解。因此，在上述约束情况下的风机最大接入容量为0.232 3 p.u.，此时整个系统的峰荷为2.954 p.u.，故接在22 号节点处风机的风电穿透功率极限为0.232 3/2.954=7.864%。

若将风电并网接入点改为30 号节点，在以上相同的假设和约束条件下，染色体[Pw30]最终得到[0.215 0]，校验其越限概率得到表4。

表4 越限概率校验

则此时的风电穿透功率极限为0.215 0/2.954=7.278%。由此看出，风电穿透功率极限的大小与风电场并网的接入点有关，合理的选择风电并网的接入点，可以有效地提高风电穿透功率极限的大小。

4 结束语

本文提出了直流概率潮流模型，通过半不变量和Gram-Charlier 级数展开方法，计算含有风电场的电力系统中支路有功潮流的概率分布。在获取支路有功功率的概率分布基础上，采用随机约束规划模型对电力系统的潮流分布、频率波动等进行约束，通过改进的遗传算法求解系统的风电穿透功率极限。最后在IEEE 30 系统中验证了模型的可行性。通过算例得到了符合置信水平的系统风电穿透功率极限数值。同时得出结论，风电并网后，距离风电场接入点越近的支路受到的影响越大，越容易过载，并指出接入点的选择对风电场规划有着重要作用。

[1]霍雨翀，范子恺.基于改进天气发生器的风速与日照模型组合预测方法研究[J].江苏电机工程，2013，32(3)：6-9，12.

[2]廖 萍，李兴源.风电场穿透功率极限计算方法综述[J].电网技术，2008，32(10)：50-53.

[3]HAN X,MU M,QIN W.Reliability Assessment of Power System Containing Wind Farm Based on Steady-state Power Flow[C]//ProbabilisticMethodsApplied to Power Systems(PMAPS),2010 IEEE 11th International Conference on.IEEE,2010:756-760.

[4]DA SILVA A M L,ARIENTI V L.Probabilistic Load Flow by a Multilinear Simulation Algorithm[C]//IEE Proceedings C(Generation,Transmission and Distribution).IET Digital Library,1990,137(4):276-282.

[5]王锡凡.电力系统优化规划[M].北京：水利电力出版社，1990：138-148.

[6]张伯明，陈寿孙.高等电力网络分析[M].北京：清华大学出版社，1996：187-188.

[7]李 军，胡 非，王丙兰，等.风速的Weibull 分布参数[J].太阳能学报，2012，33(10)：667-1671

[8]张粒子，舒 隽，林宪枢，等.基于遗传算法的无功规划优化[J].中国电机工程学报，2000，20(6)：5-8.