基于时域多周期同步和频域代数运算的谐波检测法

李安娜，黄家晖，熊杰锋

(1.东南大学电气工程学院，江苏南京 211189；2.江苏省电力公司电力科学研究院，江苏南京 211103)

谐波和间谐波测量是谐波问题中的一个重要分支，也是分析治理谐波问题的出发点[1]和主要依据。谐波测量的主要作用[2]有：（1）鉴定实际电力系统和谐波源用户的谐波水平是否符合标准的规定；（2）用于谐波源设备和其他电气设备调试、投运时的测量，以确保设备投运后电力系统和设备的安全经济运行；（3）谐波故障的诊断；（4）实时补偿设备（有源电力滤波器（APF）等）补偿的依据等。

目前IEC 推荐的谐波检测算法，其本质为离散傅立叶变换（DFT）算法。考虑电网信号的波动性，该方法截取“一定时间宽度”的数据进行分析，国际电工委员会（IEC）推荐采样窗宽为200 ms，5 Hz的频率分辨率[3，4]。由于IEC 算法精确计算的前提是尽量实现同步采样，因而规定10 周波的最大同步偏差不得超过±0.03%，同时规定同步偏差超过该值时必须对时域采样信号加Hanning 窗以消弱同步偏差对精度的影响。调整采样策略减小同步偏差以实现采样的尽可能同步，主要包括软件同步和硬件同步法。其中软件同步法有双速率采样[5]、优化选择采样点数[6]2 种方法；硬件同步则通过增加锁相环硬件电路对信号进行实时频率跟踪，实时调整采样频率，实现同步采样。因电网频率总在波动，无论软件还是硬件同步，在采用快速傅立叶算法进行谐波计算时将引入非均匀采样导致的误差。鉴于此，提出一种电网谐波数字测量新方法：时域多周期同步采样的频域代数运算法。该方法首先将多周期同步采样理论应用于现场可编程门阵列（FPGA）中，以实现每10个周波电网信号的实时跟踪。在时钟频率为100 MHz时不仅保证同步偏差满足IEC 标准，同时保证10 周波的采样为均匀采样，消除了非均匀采样带来的误差。进而对计算得到的频谱信号进行简单的代数运算，可达到加Hanning窗的精度。MATLAB 仿真验证了该算法的有效性。

1 时域多周期同步采样的频域代数运算法

1.1 DFT 算法误差来源

采用DFT 算法求取谐波参数往往存在偏差，主要取决于3个方面：

（1）信号混迭，DFT 计算的信号是有限带宽信号，对于采样信号需要外加前置低通滤波器，用于滤除不需要分析的频段信号，由于不能实现理想低通滤波器，导致不需要检测的高次谐波分量与需要检测的低次谐波分量在频谱上产生混迭带来的误差；

（2）模拟数字采样芯片（ADC）、电压互感器（TV）、电流互感器（TA）所带来的误差；

（3）同步偏差，信号频谱离散示意图如图1 所示。周期信号同步采样与非同步采样示意图如图2 所示。同步采样时，图1 中Xd2（ω）或Xd1（ω）与X（ω）重合，且泄漏频谱在整次谐波点上的幅值为0，此时根据采样值可以精确地计算出各次谐波的参数，非同步时，Xd2（ω）或Xd1（ω）与X（ω）不重合，且泄漏频谱在整次谐波点上的幅值不为0，必然导致测量误差。

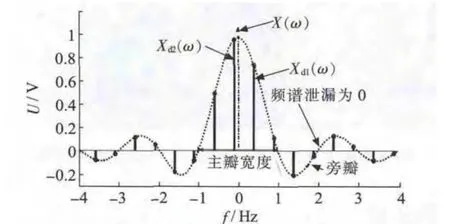
图1 频谱泄漏和栅栏效应图

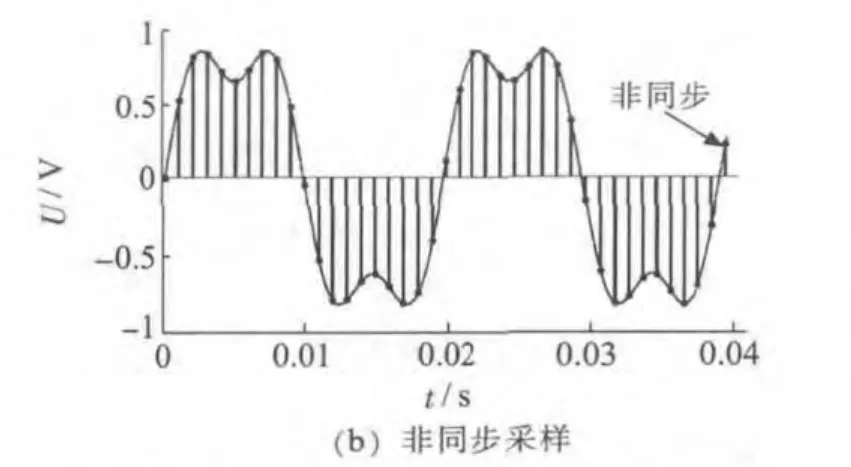
图2 周期信号同步采样与非同步采样

3个方面误差来源同步偏差一般占主要部分。实际工程中，采样是不可能严格同步的，不同步的原因主要来自电网频率的飘移和DSP（数字信号处理器）的定时误差2个方面。

1.2 多周期同步采样

多周期同步采样是一种硬件同步采样技术，可实现“整数倍”周波信号内的“均匀采样”。其硬件原理如图3 虚线框所示。将被测非正弦信号通过带通滤波和过零比较器整形后送入FPGA，由FPGA 生成同步采样控制信号实现AD 同步采样[7]。其中带通滤波器可防止对一个周波内有多个过零点的波形出现误检，如图4 所示。多周期同步采样原理如图5 所示。

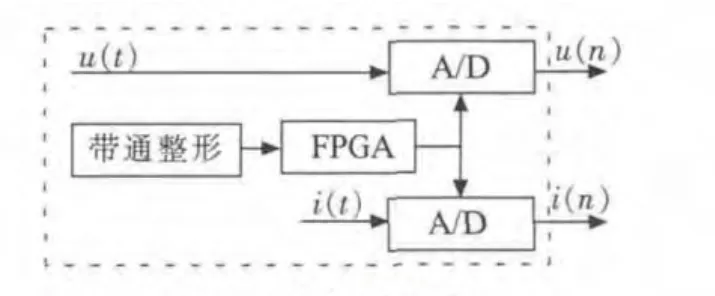
图3 硬件原理图

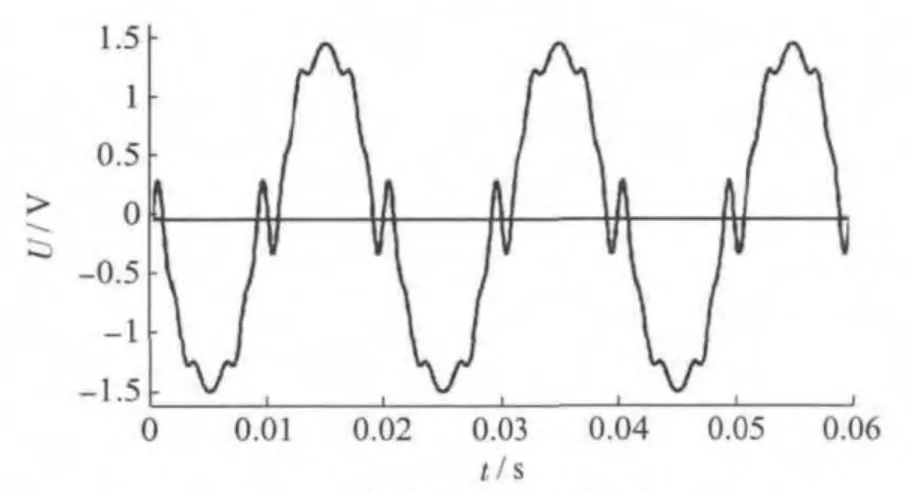
图4 电压时域波形

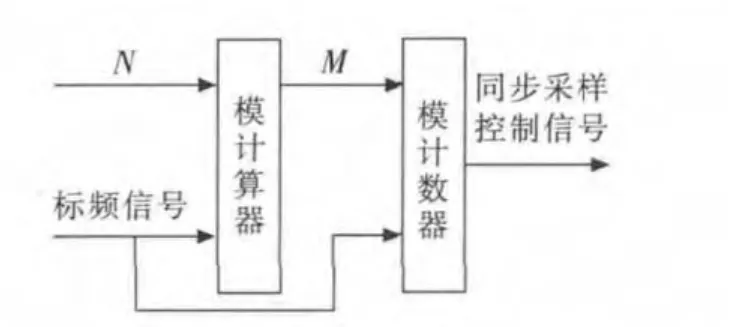
图5 多周期同步采样

以p个工频周期信号作为参考闸门信号，经电网信号上升沿同步后生成实际闸门信号，将频率较高的标频信号（100 MHz）作为填充脉冲对实际闸门进行计数得到N，由式（1）得到采样模值M，进而输出下一个测量区间的同步采样控制信号。

式（1）中：S为每周波采样点数。

设标频信号的频率和周期分别为f0，T0，被测工频信号周期的实际值和测量值分别为Tx，Tx'，采样窗口长度为p个工频周期，则：

被测信号周期的绝对误差为：

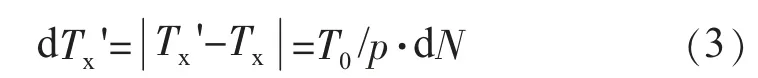
式（3）中，dN=±1，其相对误差为：

由式（4）可知，被测工频信号的周期误差与脉冲计数值N 有关，标频信号频率f0越高，p 值越大，误差越小。设相邻2个10 周波的采样区间基波频率不变，图6 给出基波频率为49.5～50.5 Hz，步进0.000 1 Hz，p=8，f0=100 MHz时，采用多周期同步采样时10个周波的同步偏差（0.01%）。由图6 可见，10个周波的同步误差小于0.002%。

图6 多周期同步采样同步误差

1.3 频域代数运算

每10 周波采样同步偏差小于±0.03%时，IEC 采样矩形窗对信号加窗频谱计算，当采样的同步偏差超过该设定值时，IEC 推荐采用加Hanning 窗后进行频谱计算。矩形窗和Hanning 窗的归一化幅频特性如图7 所示。

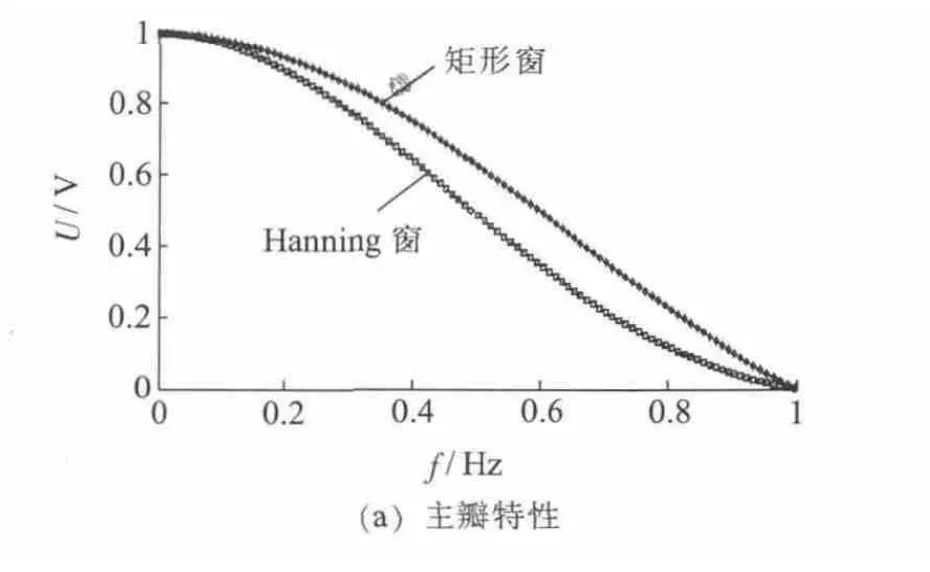
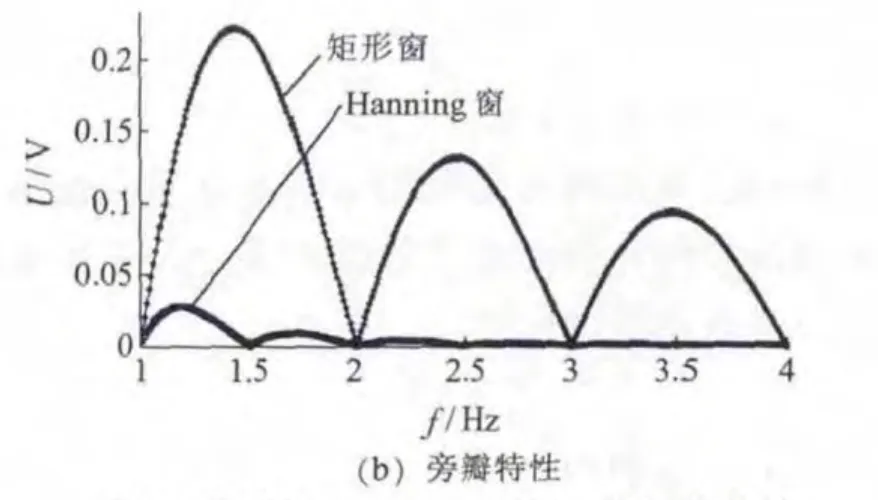
图7 矩形和Hanning 窗归一化幅频特性

由图7 可见当矩形窗和Hanning 窗在保证主瓣分辨率相同的情况下，Hanning 窗的各次旁瓣远小于矩形窗旁瓣，可以有效地削弱同步偏差对精度的影响。时域中对采样信号直接加Hanning 窗将带来运算量的增加，以每10 周波2048 点为例，每次频谱计算需要额外增加2048 次乘法运算。本文提出一种频域代数运算法，先对时域采样信号直接求取矩形窗频谱，进而采用下式：

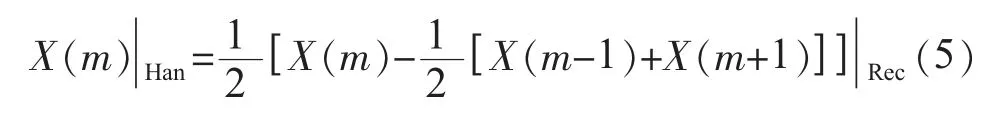
在频域中可直接得到加Hanning 窗的频谱值，频域代数运算法矩形窗频谱运算量与传统方法一样，移位和加减运算量远小于2048 点乘法运算。

1.4 硬件配置和算法步骤

时域多周期同步采样的频域代数运算法具体实现时一种硬件配置方案和算法步骤如图8 所示。

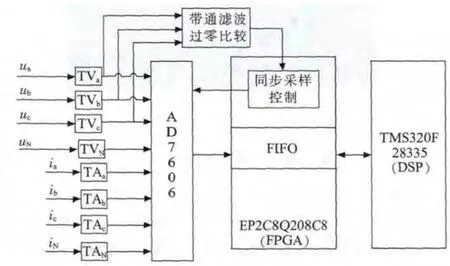
图8 新方法硬件配置

（1）TV 和TA：用于实现电气隔离和信号变换，具体选择时需要考虑互感器的带宽、线性度和精度；

（2）8 路同步采样芯片AD7606:16 位AD，在同步采样控制下，实现电压和电流同步采样；

（3）带通滤波和过零比较器：非正弦信号通过由通用运放LM258 实现的二阶带通滤波电路提取出基波分量，将该分量经LM293 实现的过零比较电路生成“被测信号”送入FPGA；

（4）FPGA：由EP2C8Q208C8 实现同步采样控制和16 位FIFO（先进先出）；

（5）DSP:在浮点TMS320F28335 中[8]，将FIFO存放的电压采样信号和电流采样信号进行FFT 运算得到各次谐波值。

2 仿真实验

为验证本文所提算法的有效性和高精度，采用MTALAB 对该方法进行验证。仿真信号按照电能质量监控终端测试的要求，为简便起见，取基波电压有效值为标幺值1，2 次至50 次谐波电压有效值分别为基波有效值的0.5%UN和3%UN，各次谐波有效值允许误差分别为0.05%UN和5%UH，其中UN为基波电压有效值，UH为谐波电压有效值。其电压信号时域波形分别如图9 和图10 所示。

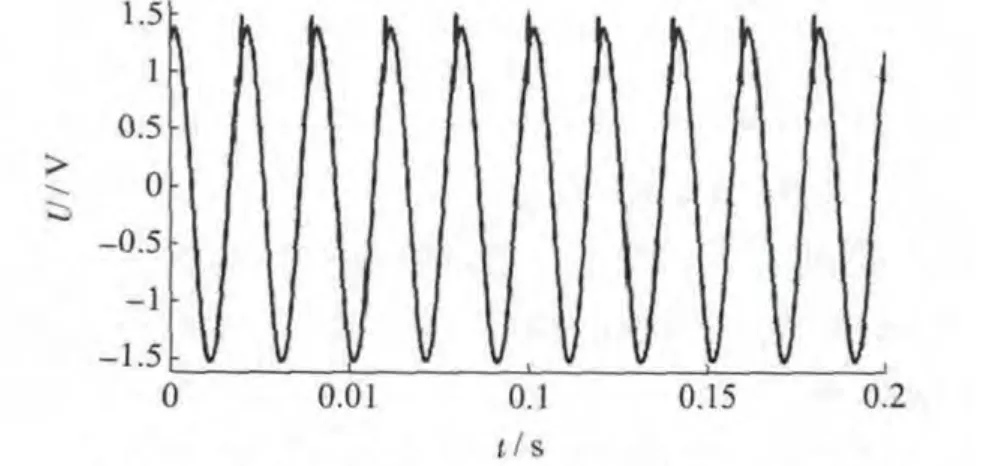
图9 谐波电压有效值为基波有效值0.5%波形

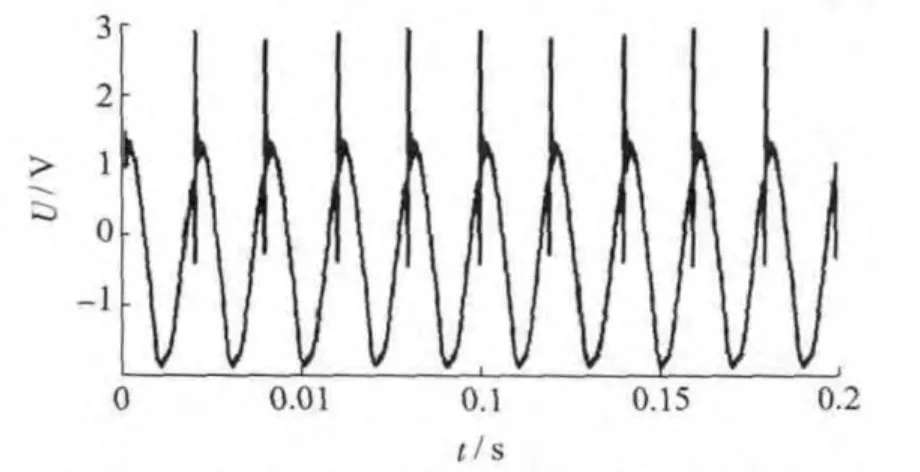
图10 谐波电压有效值为基波有效值3%波形

前文表明多周期同步采样法每10 周波同步偏差小于0.002%，为更好说明本文方法的有效性，实际仿真中选取同步偏差仅为0.02%。图11 和图12 给出此时2个算例的谐波计算精度，由图11 和图12 可见，即便按此同步偏差，谐波计算精度仍均满足电能质量监控终端谐波测量精度要求，精度满足国标A 级标准。

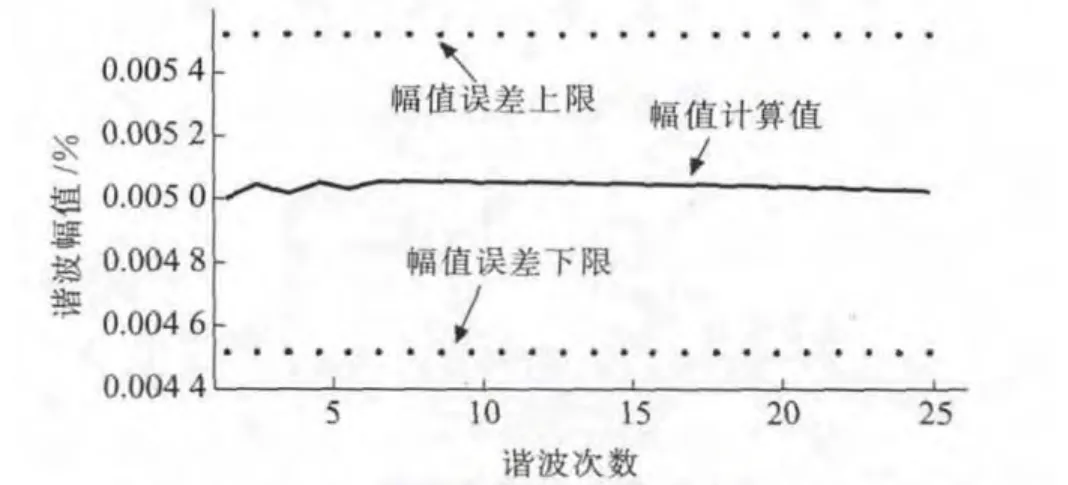
图11 谐波电压有效值为基波有效值0.5%测量结果

3 结束语

本文提出了一种电网谐波数字测量新方法，即时域多周期同步采样频域代数运算法。该方法主要优点：

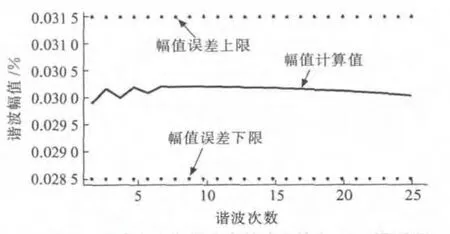
图12 谐波电压有效值为基波有效值3%测量结果

（1）采用基于FPGA的多周期同步采样技术，可实现每10 周波同步采样误差小于0.002%，远小于IEC 规定的同步偏差限值，而且随着FPGA 主频的不断提升，采样同步偏差越来越小；

（2）提出根据矩形窗频谱进行简单的移位和加法运算，以达到加Hanning 窗函数的谐波计算精度，相对传统时域加窗法运算速度更快。

由于该方法充分考虑了采样同步策略和算法实现的实时性，其同步偏差小于IEC 限值一个数量级，其谐波计算精度满足国标A 级标准。本文同时给出该方法具体实现的一种硬件配置方案，该方案将用于某种高精度电能质量分析仪的设计中。

[1]王兆安，杨 君，刘进军，等.谐波抑制和无功补偿[M].北京：机械工业出版社，1998：35-37.

[2]吕润馀.电力系统高次谐波[M].北京：中国电力出版社，1998：185-187.

[3]Gneral Guide on Harmonics and Interharmonics Measurements，for Power Supply Systems and Equipment Connected Thereto，IEC Std[S].61000-4-7，2002:27.

[4]Power Quality Measurements Methods，Testing and Measurement Techniques,IEC Std[S].61000-4-30，2002:37.

[5]方伟林，王立功.双速率同步采样法在交流测量中的应用[J].电测与仪表，1997，34(4)：21-23.

[6]潘 华，黄 纯，王联群.电力参数微机测量中采样周期的优化校正方法[J].电力系统自动化，2002，26（5）：71-75.

[7]张志文，王承林，王 伟，等.新型多周期同步和倍频锁相的频率跟踪技术[J].电力系统及其自动化学报，2009，21（5）：119-123.

[8]李宁峰.基于TMS28335的智能电网快速采样系统设计[J].江苏电机工程，2012，31（6）：35-39.