引入虚拟电抗的独立运行微电网改进下垂控制

黄春燕

(南通供电公司，江苏 南通 226000)

微电网是解决分布式电源（DG）并网的有效途径[1]。根据不同种类微电源的输出特性，微电源的控制方法有下垂控制、PQ 控制和Vf 控制[2]。下垂控制模拟传统发电机的下垂特性来实现并联控制，利用P-f和Q-V下垂特性实现对有功和无功的解耦控制[3]。但P-f和Q-V下垂控制适用的一个前提条件是线路的电抗X 远大于其电阻R，而在低压微电网中线路电阻值通常大于线路电抗值，功率传输P-f和Q-V的对应关系不再存在，逆变型微电源并联运行采用下垂控制将无法实现功率的正确分配。

为避免功率控制耦合现象，有些学者提出虚拟同步旋转轴的解耦控制策略[4]。文献[5]提出虚拟有功无功传输控制的方法，利用正交矩阵变换将实际的PQ 值转换为虚拟PQ 值。文献[6]提出可以在逆变电源输出端和负载之间串联一个大的电感或者安装隔离变压器，以保证逆变电源到负荷之间的阻抗为感性，这样P-f和Q-V下垂控制的前提条件就能够满足了，但是电感的投入增加了系统的体积和成本，当输出电流中含有高次谐波成分时，电感上将产生很大的谐波压降，从而使输出电压失真严重。文献[7]通过设计控制器参数使输出阻抗呈感性，但是阻抗大小不能确定。

1 DG 并网逆变器结构及控制原理

1.1 DG 并网逆变器结构

微电网由DG、储能装置、负荷、传输线路和控制系统等元件和模块组成。绝大多数DG 通过逆变或者整流/逆变的电力电子变换器接入微电网母线。假设DG 直流侧装设有储能装置，因此可将DG 并网逆变器侧电压视为一个恒定值，则DG 并网逆变器结构如图1 所示。

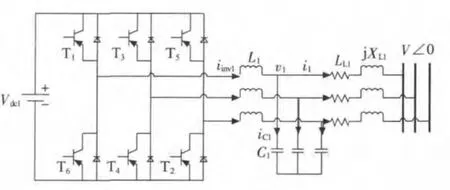
图1 DG 并网逆变器结构

图1 中，Vdc1为DG 直流侧电压；iinv1为并网逆变器交流侧输出电流；L1为滤波电感；v1为滤波电容电压，也是DG 输出电压（忽略滤波电阻）；iC1为滤波电容电流；C1为滤波电容；i1为DG 输出电流；RL1为DG 并网传输线电阻；XL1为DG 并网传输线电抗；为微电网交流母线电压。

1.2 并网逆变器控制原理

逆变器控制方法由最初的无环控制[8]，改进成单环控制[9]，现在常采用电压电流双环控制[10，11]。选择滤波电容电流作为控制变量构建电流内环，选取滤波电容电压作为控制变量构建电压外环。电压外环能够保证DG输出电压的稳定，同时给电流内环提供电流参考值；电流内环按照电压外环输出的电流参考值进行电流控制，对非线性负载扰动的适应能力增强，输出电压的谐波含量小。电流内环采用比例（P）控制，电压外环采用比例—积分（PI）控制，简化的双环控制系统结构如图2 所示。

图2 简化的双环控制系统结构

图2 中，KP，KI是外环比例积分系数，K 是内环比例系数，KPWM是逆变器放大系数。以V1ref为输入，V1为输出，可以得到电压环传递函数：

该传递函数的前半部分体现了控制系统的稳定性，后半部分体现了负载电流所产生的扰动的影响，可简化为：

式（2）中：G（s）为电压比例增益传递函数，理想情况下G（s）=1；Zinv（s）为逆变器等效输出阻抗。

由式（1）可知，Zinv（s）不仅与滤波器参数有关，还与控制器参数有关，当滤波器参数确定时，可以通过设计合适的控制器参数，使Zinv（s）呈感性或阻性。由图2可得电压环的开环传递函数：

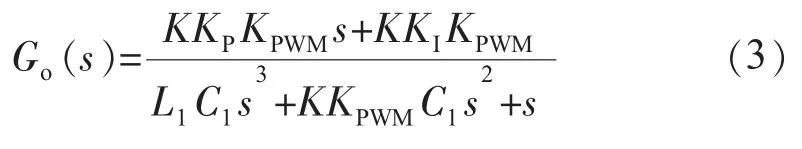
2 基于控制器参数设计的下垂控制

2.1 下垂控制原理

以2个电源并联运行为例分析下垂控制原理，如图3 所示。

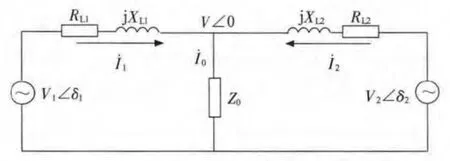
图3 功率传输示意图

图3 中，设Vk∠δk为第k个电源的输出电压，k=1，2，…；RLk和XLk分别为第k个电源的并网传输线电阻和电抗；V∠0为负荷端交流母线电压，也是负载Z0上的电压；I˙k为第k个电源的输出电流，I˙0为负载电流。第k个电源输出的有功功率和无功功率分别为：

在高压输电系统中，传输线路电抗远大于电阻，即XLk>>RLk，可以将RLk忽略，并且功率角δk很小，可近似得到sin δk≈δk，cos δk≈1，则式（4）和式（5）化简为：

在低压配电系统中，传输线路电阻通常大于电抗，即RLk>XLk；考虑到功率角δk通常很小，则式（4）和式（5）化简为：

由此可见，低压、高压系统的功率传输表达式有所不同，从而下垂控制的表达式也有所不同。当线路传输线阻抗中电抗远大于电阻时，采用有功-频率（P-f）和无功-电压（Q-V）的解耦控制方式；反之采用有功-电压（P-V）和无功-频率（Q-f）的解耦控制方式。根据线路的阻抗特性，选择正确的下垂控制方式才能实现有功无功的解耦控制。

2.2 下垂控制的不足

微电网属于低压配电网范畴，传输线路呈阻性，根据上文的分析，宜采用P-f和Q-V的反调差下垂控制方式，但是现有的逆变电源下垂控制方法大多采用P-f和Q-V的传统下垂控制方式。设置控制器的参数，使其既能保证控制系统的稳定性，又能保证控制系统具有一定的稳态和动态性能指标，同时还能保证在工频附近逆变器等效输出阻抗Zinv（s）呈感性，并且该值与线路实际阻抗之和也呈感性。取滤波器参数L=0.8 mH，C=1600 μF，为了得到合适的控制器参数，采用经验法[12]和频域响应曲线相结合，得到控制器参数K=0.6，KP=10，KI=100时，Zinv（s）呈感性，此时Zinv（s）的频域响应曲线如图4 所示。可以看出，逆变器等效输出阻抗Zinv（s）在50 Hz 附近呈感性，在高频段呈阻性。

图4 Zinv(s)的频域响应曲线

此时，电压环的开环传递函数Go（s）的波特图如图5 所示。从图5 可知系统稳定，具有一定的幅值裕度和相位裕度。

图5 Go(s)的波特图

以上分析表明，整定的K，KP，KI既能够满足系统控制性能的要求，也能保证逆变器等效输出阻抗Zinv（s）呈感性。接下来分析Zinv（s）的数值大小，将L，C，K，KP，KI值代入Zinv（s）计算公式，令s=j314，求得频率为50 Hz时逆变器等效输出阻抗：

由式（10）可见，此时逆变器的等效输出电抗值非常小，不足以使线路具有高压输电线路的特性。保持L和C 值不变，在K∈[0.001，10]，KP∈[0.001，1000]，KI∈[0.001，3000]的范围内寻找Xinv的最大值为：当K=0.001，KP=0.001，KI=159时，=0.287 3。但是，此时K 值很小，控制系统的快速性很差，如果外界发生一个小扰动，则系统达到稳定状态所耗费的时间很长。其次，如果逆变电源与负载之间的实际低压线路长度较长，则该值就不足以使可控电源与负载之间的等效线路阻抗具有高压线路的感性性质。

以上分析表明，控制器参数设计法不能同时满足系统性能和逆变器等效输出阻抗值的要求，所以本文引入虚拟电抗的思想对下垂控制加以改进。

3 引入虚拟电抗的改进下垂控制

为了使逆变电源与负载之间的输出阻抗呈感性，又不在逆变器的输出端真正接入一个电感，可以采用“虚拟电抗”的概念，在逆变器的输出端模拟出一个远大于逆变器到负载之间电阻的虚拟电抗[13]。通过在逆变电源电压电流双环控制的电压指令值中减去虚拟电抗上的压降来实现模拟出一恒定的电抗，记虚拟电抗为Xvir，得到新的电压参考值：

图6 引入虚拟电抗后的闭环系统控制框图

此时逆变器电压环传递函数：

由式（12）可以看出，等效输出阻抗Z'kinv（s）=sLkvir+Zkinv（s），当Lkvir取远大于逆变器到负载电阻值时，就可确保线路阻抗呈感性，而且电流电压环参数的设计确保了Zkinv（s）对于基频呈感性，进一步增大了等效电抗。采用虚拟电抗法将逆变电源与负载之间的电抗值加以改变，可以保证线路阻抗主要呈感性，满足了下垂控制的前提条件，但是也牺牲了系统输出电压的稳态精度，输出电压值较未采用虚拟电抗法时有所下降。因此，可对下垂特性曲线进行改进，将虚拟电抗上的压降纳入考虑范围，以提高输出电压稳态精度[13]。因虚拟电抗上不消耗有功功率，只消耗无功功率，所以只需修正Q-V下垂特性曲线。定义逆变电源输出电压和负载电压之差ΔVk与逆变电源发出的无功功率Qk之比为Kk。引入虚拟电抗后，线路呈感性，按式（7）可得：

由于需控制Vk在一定范围内变化，一般为额定值的±5%，且Xkvir为设定的电抗值，所以Kk可近似视为一恒定值。2个逆变电源修正前Q-V下垂系数分别为n1和n2，最大无功功率输出为Q1max和Q2max，允许电压最小值为Vmin。如图7 所示。

当2个逆变电源均发出最大无功功率时，Xkvir上的压降为KkQkmax，从而将Q-V下垂特性曲线的电压最小值修正为：

图7 修正前后的Q-V 下垂特性曲线

由此可得修正下垂特性曲线的Q-V下垂系数为：

此时下垂特性曲线的表达式：

将修正后的下垂特性曲线用在图6 中，有利于提高电压稳态精度。

综上所述，引入虚拟电抗后，可以保证逆变电源到负载之间的线路阻抗呈感性，从而P-f 和Q-V下垂特性曲线能够正确实现功率分配；采用修正后的下垂控制曲线提高了电压的稳态精度。

4 仿真分析

为了验证基于虚拟电抗的改进下垂控制的有效性，将传统的下垂控制与基于虚拟电抗的改进下垂控制进行仿真对比。采用的微电网仿真系统结构如图8所示。

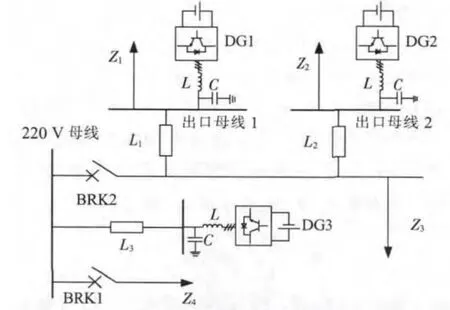
图8 微网仿真系统结构

图8 中，3个DG 并联运行，额定电压Vdc为800 V，容量均为10 kW，母线电压等级为220 V；线路1，线路2，线路3的长度分别为200 m，300 m，200 m，线路单位阻抗参数为r=0.641 Ω/km，x=0.101 Ω/km（电抗参数为工频值）；负荷采用恒阻抗模型，参数设置为Z1=Z2=（50+j3.14）Ω，Z3=Z4=（30+j12.56）Ω。

设3个DG的P-f 下垂系数m1:m2:m3=4×10-5:6×10-5:12×10-5=2:3:6，Q-V 下垂系数n1:n2:n3=3×10-5:3×10-5:3×10-5=1:1:1，3个DG的控制器参数：L=0.6 mH，C=1500 μF，RL=0.01 Ω，K=0.6，KP=10，KI=100。

4.1 传统下垂控制仿真

DG1，DG2，DG3 均采用传统下垂控制，t=2 s时，开关BRK1 闭合，负荷Z4投入，仿真结果如图9 所示。

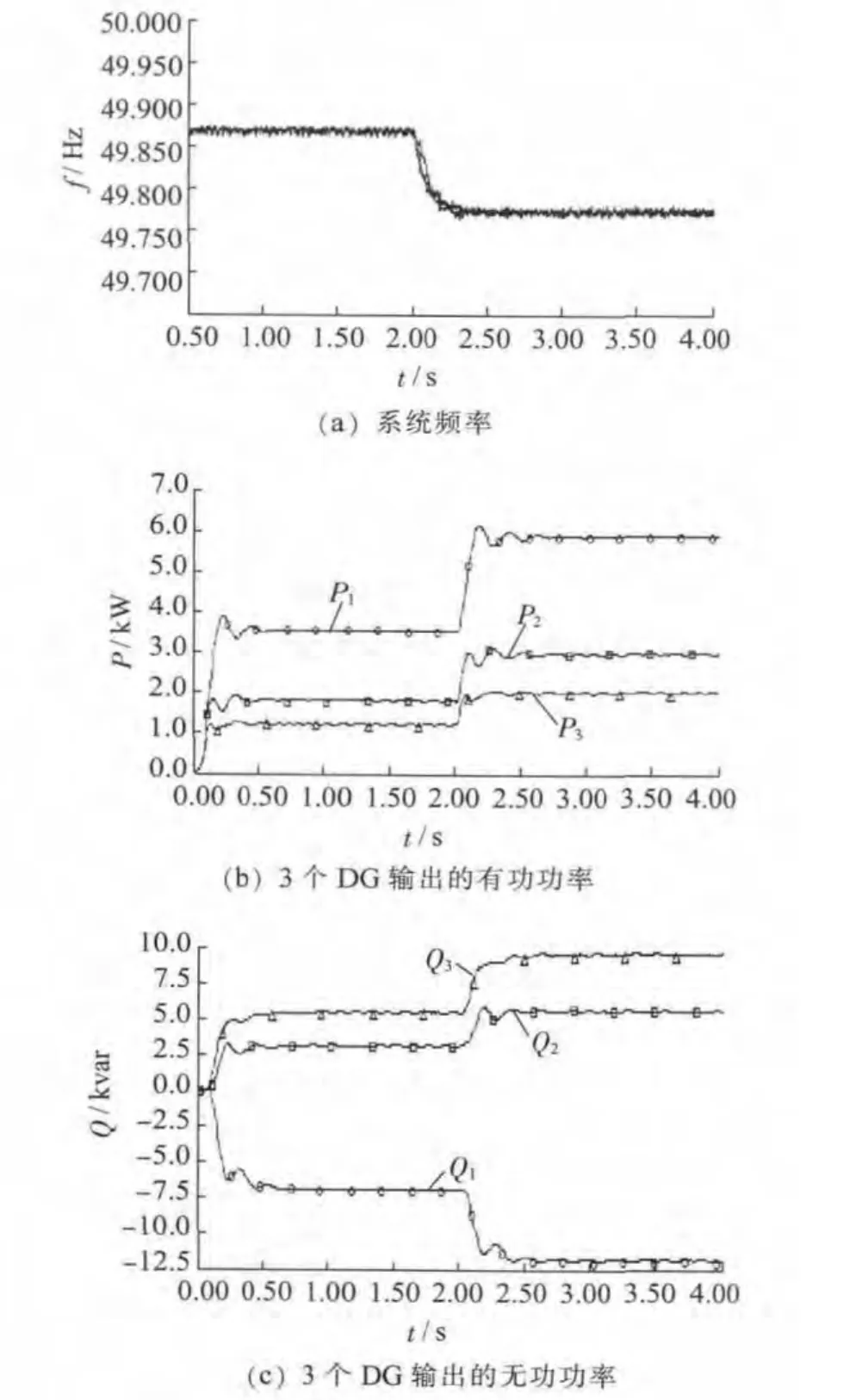
图9 传统下垂控制仿真结果

仿真启动后微网很快达到稳定。由图9（a）可知，f1=f2=f3，即3个DG的频率输出一致，则微网的频率唯一，否则微网一直处于频率不稳定状态。t=2 s时，负荷Z4投入，3个DG 增加有功出力，系统频率下降，符合一次调频特性。由图9（b）可知，有功出力始终按照有功下垂系数的反比承担负载有功功率，P1:P2:P3=6:3:2。t=2 s时Z4投入，经过一段时间后，微网再次达到稳定，3个DG 按比例共同承担新增的负载有功功率，此时仍然有P1:P2:P3=6:3:2。由图9（c）可知，在整个仿真过程中，无功出现了严重的不平衡：DG1 吸收无功，DG2 和DG3 发出无功，3 者之和为负荷所需无功，当Z4投入后，3个DG的无功差别更大。出现上述现象的原因是低压配电网线路呈阻性时，如式（9）所示，逆变电源输出的无功功率不仅与电压幅值有关，而且与相角有关，因而传统下垂控制失效，无功功率得不到正确分配。

4.2 基于虚拟电抗的改进下垂控制仿真

DG1，DG2，DG3 采用基于虚拟电抗的改进下垂控制，取L1vir=L2vir=L3vir=4 mH，t=2 s时负荷Z4投入，仿真结果如图10 所示。

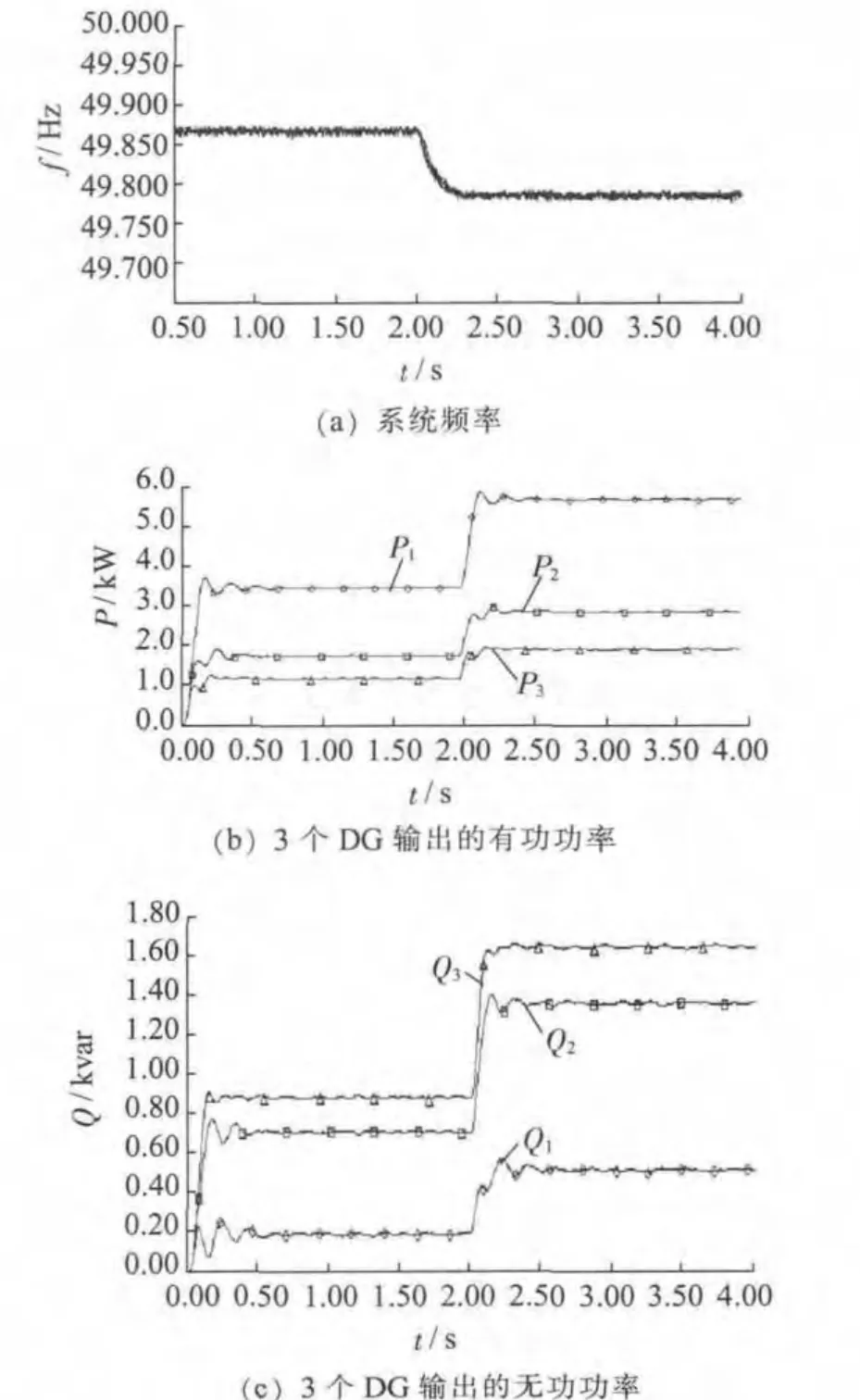
图10 基于虚拟电抗的改进下垂控制仿真结果

由图10 可知，3个DG 均采用基于虚拟电抗的改进下垂控制之后，微网同样能够稳定运行。图10（a）表明，3个DG的频率输出一致；图10（b）表明，3个DG始终按有功下垂系数的反比共同承担负载有功功率。图10（c）表明，采用基于虚拟电抗的改进下垂控制后，DG1，DG2，DG3 能较好地实现无功负荷的均分，所发出的无功均为正值，避免了部分发出无功，部分吸收无功的情况。值得注意的是，虽然引入了虚拟电抗且n1:n2:n3=1:1:1，但Q1:Q2:Q3≠1:1:1，其原因有2 点：（1）虽然修正了下垂特性曲线，将虚拟电抗上消耗的无功纳入了考虑范围，但是只是采取了近似计算方法，由下垂特性曲线计算出来的电压参考值精度降低了；（2）实际线路的长度不一致，当各个逆变电源的输出外特性和线路阻抗不一致时，仅利用Q-V 下垂控制是无法实现DG 输出无功严格按无功下垂系数的反比分配的，即使在线路为纯感性的情况下也是如此，这一点有别于P-f下垂控制。3个DG 输出的电流与采用传统下垂控制时相比，均有所下降，如表1 所示。

表1 2 种控制方法电流比较 A

由表1 可知，改进下垂控制使得无功能在DG 中合理分配，避免了某些DG的无功过载，因此大大降低了线路电流。

5 结束语

P-f和Q-V 下垂控制能实现功率分配的前提条件是线路呈感性。分析表明，通过设计控制器参数使得微电网中线路呈感性的方法不能同时满足系统性能和逆变器等效输出阻抗值的要求。因此，基于虚拟阻抗的思想，在逆变电源的输出端模拟出一个远大于逆变器到负载之间电阻的虚拟电抗，确保线路呈感性，从而满足了P-f和Q-V 下垂控制的应用条件。仿真表明，该方法可以确保P-f和Q-V 下垂控制在阻性线路环境中有较好的功率分配效果，验证了该方法的有效性。

[1]鲁宗相，王彩霞，闵 勇，等.微电网研究综述[J].电力系统自动化，2007，31(19)：25-34.

[2]王成山，肖朝霞，王守相.微网综合控制与分析[J].电力系统自动化，2008，32(7)：98-103.

[3]肖朝霞，王成山，王守相，等.含多微型电源的微网小信号稳定性分析[J].电力系统及其自动化，2009，33(6)：81-85.

[4]朱永利，姚建国，刘 骥.微电网关键技术及研究现状.江苏电机工程[J].2012，31(3)：81-84.

[5]BRABANDERE K D,BOLSENS B,DEN KEYBUS J V,et al.A Voltage and Frequency Droop Control Method for Parallel Inverters[J].IEEETransonPowerElectronics,2007,22(4):1107-1115.

[6]GUERRERO J M,MATAS J,VICU?A L G,et al.Decentralized Control for Parallel Operation of Distributed Generation Inverters Using Resistive Output Impedance [J].IEEE Trans on Industry Electronics,2007,54(2):994-1004.

[7]王成山，肖朝霞，王守相.微网中分布式电源逆变器的多环反馈控制策略[J].电工技术学报，2009，24(2)：100-107.

[8]ENGLER A.Applicability of Droops in Low Voltage Grids [J].International Journal of Distributed Energy Resources,2005,01(1):1-6.

[9]LASSETER R H.Microgrids and Distributed Generation[J].Journal of Energy Engineering American Society of Civil Engineers,2007,133(3):144-149.

[10]HERNANDEZ-ARAMBURO C A,GREEN T C.Fuel Consumption Minimization of a Microgrid [J].IEEE Trans on Industry Applications,2005,41(3):673-681.

[11]陈 波，朱凌志，朱晓东.并网光伏电站低电压穿越仿真与分析[J].江苏电机工程，2012，31(5)：13-17.

[12]薛亚丽，李东海，徐 峰，等.最优PI 控制器参数整定及评价[J].清华大学学报（自然科学版），2004，44(8)：1067-1070.

[13]LI Y W,KAO C N .An Accurate Power Control Strategy for Power-electronics-interfaced Distributed Generation Units Operating in a Low-voltage Multibus Microgrid [J].IEEE Trans on Power Electronics,2009,24(12):2977-2988.