一个微分差分方程的N-孤子解及动力分析

李 琪， 张 文

(东华理工大学理学院，江西 抚州 344000)

寻找孤子方程的精确解是数学物理和孤立子理论中一个重要的研究课题。一些研究方法，如反散射变换法，达布变换，贝克隆变换，Hirota 方法，朗斯基技巧，变量分离法和Painlevé 分析等可以用来求解。其中获得孤子解的直接而有效的方法是Hirota 方法(Hirota，1971)。该方法引入双线性导数，寻找合适的变量变换，化孤子方程为双线性导数方程，然后将扰动展开式代入到双线性导数方程中，在一定条件下该展开式截断至有限项，得到线性指数函数形式的单孤子解，双孤子解的精确表达式和N-孤子解的一般表达式。Hirota 方法已广泛应用在连续孤子可积系统，并已推广至高维和离散可积系统。孤子方程的精确解、可积性分析及数值模拟方法的应用也是研究的热点(高云，2010;李琪，2009;张文，2012)。

非线性薛定谔方程具有深刻的应用背景，特别是近年来在金融数学领域出现了连续、离散、耦合和向量非线性薛定谔方程，甚至已有研究高阶和耦合情形(Ankiewicz，2010;Akhmediev，2011)。比如，Ivancevic 期权定价模型正是一个非线性薛定谔方程，此方程的怪波解精确的阐释了金融风暴。此方程的有理分式形式的爆破解描述了海洋怪波产生的机理。多维非线性薛定谔方程描述了两个原子的偶极子相互作用的Bose-Einstein 凝聚问题(郭柏灵，2011;Guo，2011)。非线性薛定谔方程是著名的AKNS 谱问题的一个相容性条件。作为AKNS 谱问题的离散情形，与Ablowitz-Ladik 谱问题(Ablowitz，1991，2004)联系的相关问题如可积分解(耿献国，2007)，Ablowitz-Ladik 族的对称(Zhang，2010a，b)得到探讨。本文第1 节由谱问题

导出一个微分差分方程(空间离散)

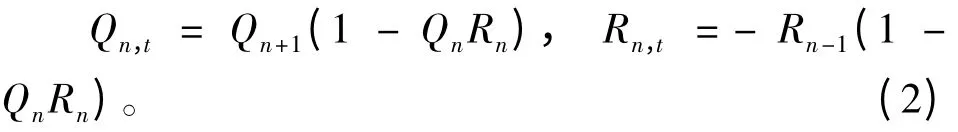
及其相应的Lax 对。第2 节给出方程的双线性导数形式和N-孤子解，并分析单孤子的形状和双孤子的相互作用及退化情形。

1 微分差分方程的推导

考虑离散谱问题(1)和时间发展式

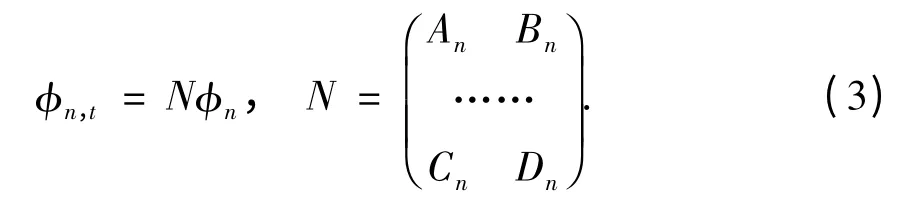
其中，φn= φ(t，n)，Qn= Q(t，n)，Rn= R(t，n)(n ∈Z)是依赖于变量t 和n 的光滑函数，当| n| 趋于无穷时，φn，Qn和Rn充分快趋于零。An，Bn，Cn和Dn是依赖于t，n 和谱参数z 的未知函数。E表示平移算子，即E(fn)= fn+1- fn。首先，由相容性条件

得到零曲率方程

若把方程(1)和(3)中的矩阵和代入零曲率方程(4)，则有

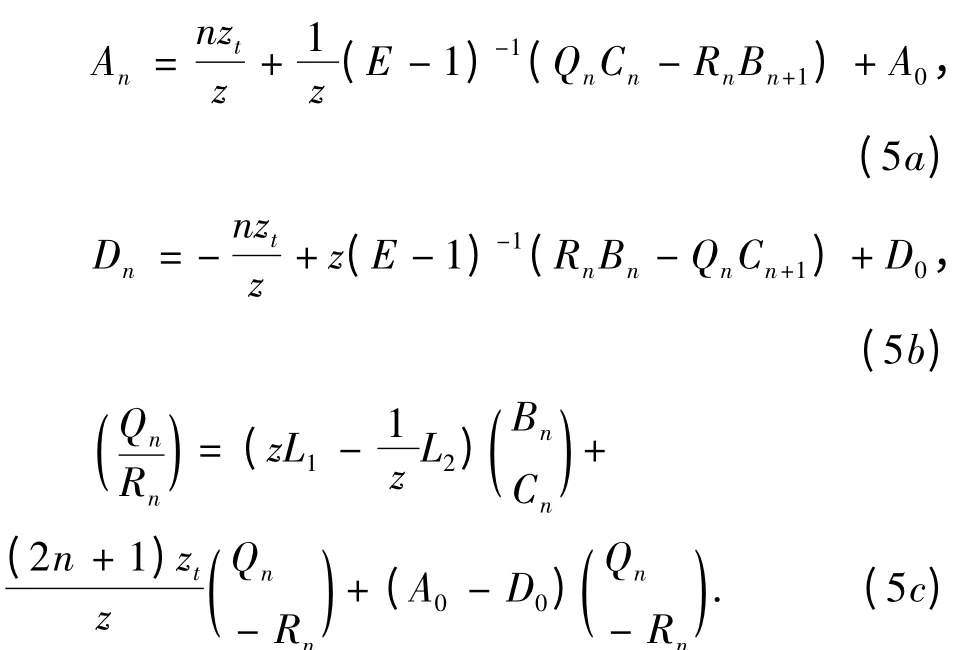
这里算子L1和L2分别定义为

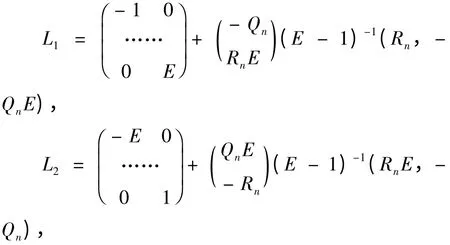
A0和D0是与n 无关的常数。为推导出方程(2)，假设z 与t 无关，且

从而得到方程(2)，且该方程相应的Lax 对(1)和(3)中

2 微分差分方程的N-孤子解

本节中，定义微分算子Dn和eDn为

为得到方程(2)的N-孤子解，作变量变换

则方程(2)可化为双线性导数形式

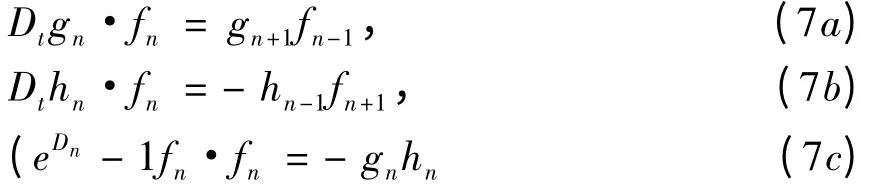
假设f(t，n)，g(t，n)和h(t，n)按ε 展成无穷级数

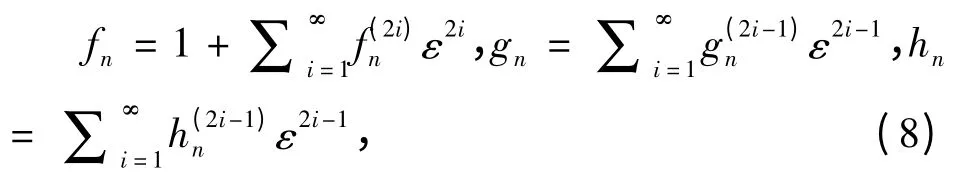
若代入方程(7)，并比较ε 的同次幂系数得

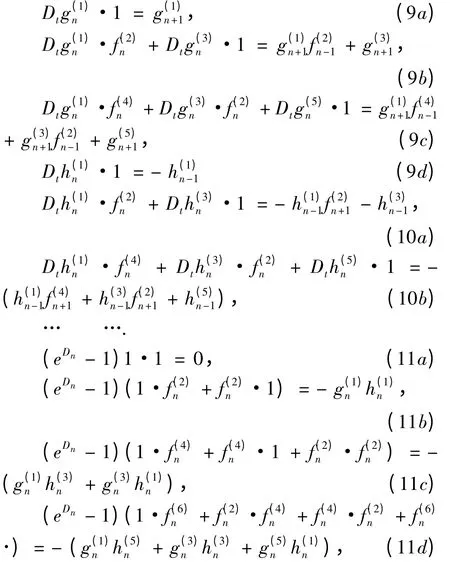
为得到方程(2)的单孤子解，由方程(9a)和(10a)，若取

代入(11)，得到

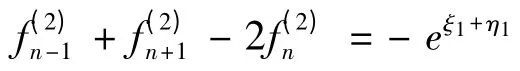
从而解得

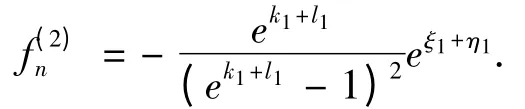
为得到方程(2)的双孤子解，由方程(8a)和(9a)，若取

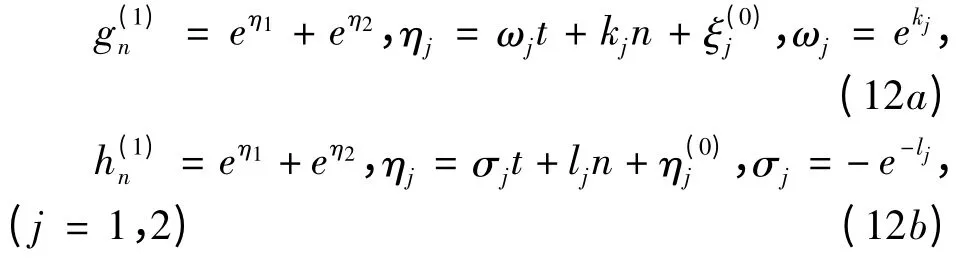
代入(11b)，得

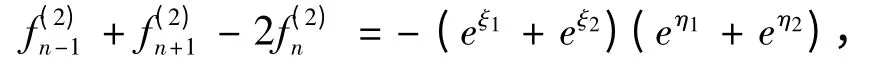
从而解得

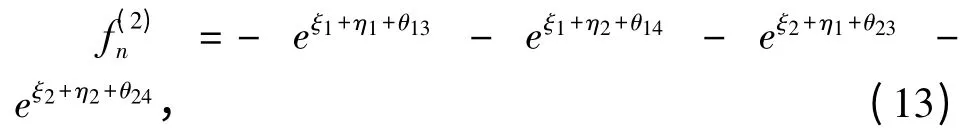
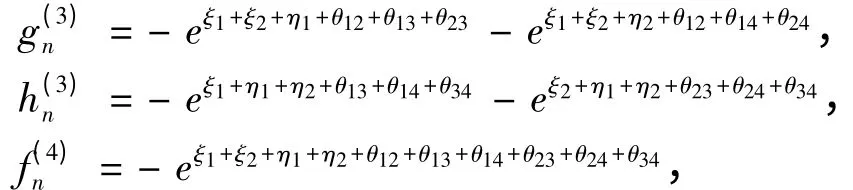
从而得到方程(2)的双孤子解为

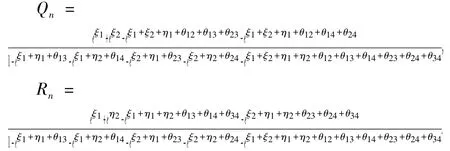
一般的，方程(2)的N-孤子解可表示为

其中

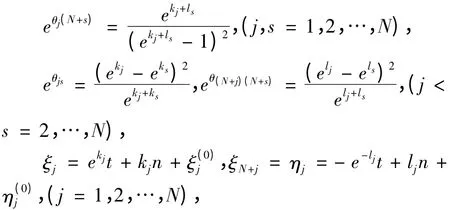
A1(μ)，A2(μ)和A3(μ)表示取遍μj=0，1 所有可能的组合，还须分别满足条件

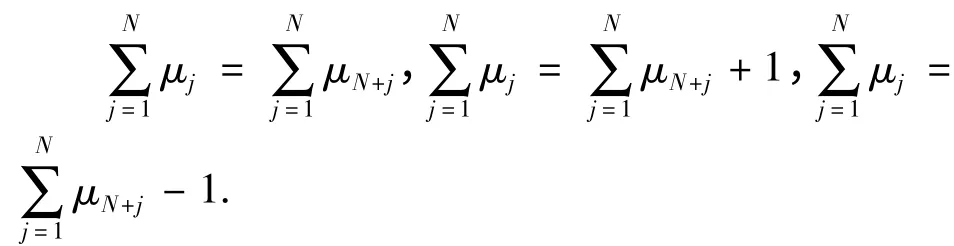
3 结论

本文给出与离散Ablowitz-Ladik 谱问题相关的方程(1.2)及其Lax 对，通过Hirota 双线性导数法，得到方程(1.2)的单孤子，双孤子和N-孤子解，并对单孤子的形状和双孤子的相互作用进行分析。此研究结果有助于推广Hirota 双线性导数法到离散Ablowitz-Ladik 方程族，得到整个方程族的-孤子解，从而进一步分析解的性质和应用。

高云，乐励华. 2010. Zakharov-Kuznetsov 方程新的周期解和孤立波解［J］. 东华理工大学学报:自然科学版，33(4):393-397.

郭柏灵. 2011. 非线性Schrödinger 方程(I):Bose-Einstein 凝聚和怪将波现象［J］. 数学进展，40(4):393-399.

李琪. 2009. 含自相容源的可积系统［J］. 东华理工大学学报:自然科学版，32(1):93-96.

张文，阮周生，邱淑芳，等，2012. 二维单裂隙-孔隙双重介质的核素迁移数学模型及参数反演［J］. 东华理工大学学报:自然科学版，35(4):422-427.

Ablowitz M J，Clarkson P A. 1991. Solitons，Nonlinear Evolution Equation and Inverse Scattering［M］. Cambridge:Cambridge University Press.

Ablowitz M J，Prinari B，Trubatch A D. 2004. Discrete and Continuous Nonlinear Schrödinger Systems［M］. Cambridge:Cambridge University Press.

Akhmediev N，Ankiewicz A. 2011. Modulation instability，Fermi-Pasta-Ulam recurrence，rogue waves，nonlinear phase shift，and exact solutions of the Ablowitz-Ladik equation［J］. Physical Review E，83(4):046603-10.

Ankiewicz A，Akhmediev N，Soto-Crespo J M. 2010. Discrete rogue waves of the Ablowitz-Ladik and Hirota equations［J］. Physical Review E，82(8):026602-7.

Geng X G，Dai H H，Zhang J Y. 2007. Decomposition of the discrete Ablowitz-Ladik hierarchy［J］. Studies in Applied Mathematics，118(3):281-312.

Guo B L，Ling L M. 2011. Rogue Wave，Breathers and Bright-Dark-Rogue Solutions for the Coupled Schrödinger Equations［J］. Chinese Physics Letters，28(11):110202-4.

Hirota R. 1971. Exact solution of the KdV equation for multiple collisions of solitons［J］. Physical Review Letters，27(18):1192-4.

Zhang D J，Chen S T. 2010. Symmetries for the Ablowitz–Ladik Hierarchy:Part I. Four-Potential Case［J］. Studies in Applied Mathematics，125(4):393-418.

Zhang D J，Chen S T. 2010. Symmetries for the Ablowitz–Ladik Hierarchy:Part II. Integrable Discrete Nonlinear Schrödinger Equations and Discrete AKNS Hierarchy［J］. Studies in Applied Mathematics，125(4):419-443.