基于MPSK信号的实用高精度的载频盲估计研究

梁亚均，姚远程，秦明伟

(1.西南科技大学信息工程学院，四川绵阳621010;2.特殊环境机器人技术四川省重点实验室，四川绵阳621010)

在现代无线电通信中，无论是民用中对信号的监测，还是军用中的电子对抗等，对信号的各种特性参数的盲估计都显得尤为重要。信号的载频估计是对信号下变频、同步、正确解调等一系列处理的基础。

当前及以前的许多信息工作者对不同类型调制信号的载频估计理论及实现方法进行过较为深入的研究。当前载频估计的方法有很多类，分为数据辅助类和非数据辅助类。数据辅助类主要用于协作式通信，非数据辅助类主要用于非协作式通信。谭舒［1］等人利用互相关累积算法对DS/BPSK信号的载频估计进行了研究，这种算法在实际使用中不是很灵活，因为它要先设定平方滤波器的参数，滤波后再对信号进行处理，这样可能会把有用信号滤除。郑鹏［2］等人采用谱相关理论对DS－SS信号进行载频盲估计，在低信噪比的情况下有很好的估计准确度，但是在进行高载波频率估计时，算法计算量太大，不利于实际应用。王戈［3］等人利用频率居中法与Welch功率谱估计方法相结合估计信号的载频，虽然相对于单独使用频率居中法性能有很大提高，但是对于搜索拐点是一个难题，搜索是一遍一遍地重复进行直到找到为止，计算量太大，不利于实现。邓振淼［4］等人把载频盲估计分为粗估计和精估计两次估计来实现，利用PSK频偏信号是分段线性相位函数，且每一段的斜率正比于频偏的性质，估计出频偏，这种算法的估计精度很好，但是它要求与码速率结合，这样就要求有一定的先验知识。Lars Haring［5］通过最大似然估计(ML)，H.Sols－Estrella［6］根据最小二乘法(LS)原理实现载频估计，但是该算法的运算量太大，给实际应用带来了困难。从W.Gardner［7］把循环谱密度函数运用到信号参数估计上以来，其算法不断得到改进，其性能也得到了提升。本文将基于循环自相关和功率谱的理论提出一种能在高速、低信噪比的情况下实现高分辨率的载频盲估计方法。先通过谱循环对载频进行第一级的粗估计，然后对采样信号进行数字下变频，最后对下变频后的信号用功率谱分析，对载频进行精确的估计。将通过理论分析和MATLAB实验仿真分析来说明新方法的正确性和性能指标以及在实际应用中怎样才能够实现此方法。

1 信号模型

MPSK信号可表示为

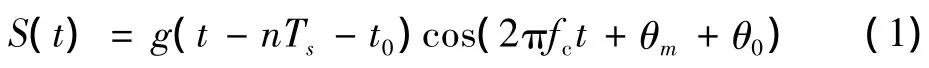
式中:Ts为码元周期;g(t)是以Ts为宽度的门函数;fc是载波频率;θm是MPSK相对应的相位变化值，同一码元内θm取值相同;t0是信号的起始时刻;θ0为信号初始相位。在实际的应用中，由于信号的发送与接收经常受成形滤波的影响，使PSK信号的包络呈现为升余弦形式。采用的升余弦滤波器为

式中:β为滚降因子，β∈［0，1］。为了简化分析，假设t0=0，θ0=0，此假设并不影响分析结果。经过成形滤波后的MPSK信号可表示为

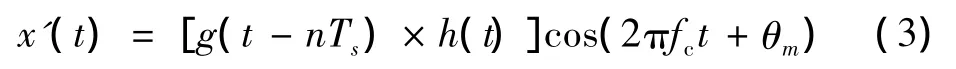
设接收到的信号为

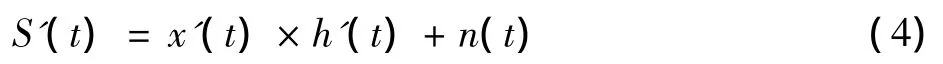
式中:x(t)为接收信号部分;h'(t)为信道的脉冲响应;n(t)为加性噪声。为了分析方便，令接收信号为

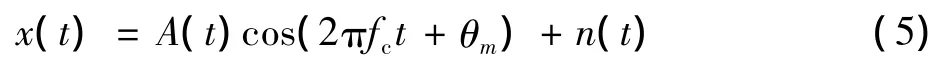
式中:A(t)为接收信号的包络。

2 载频盲估计算法分析

2.1 谱循环的基本理论

设x(t)为一循环平稳随机过程［8］，定义其自相关函数为

式中:T为码元周期;τ为延迟时间;E［·］表示求均值，则信号的循环自相关函数为

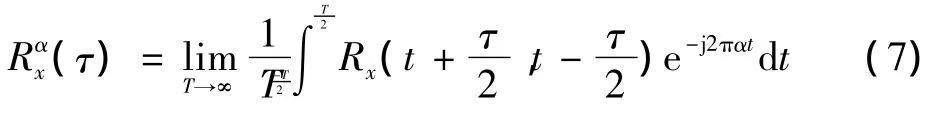
对于式(7)可进一步表达为

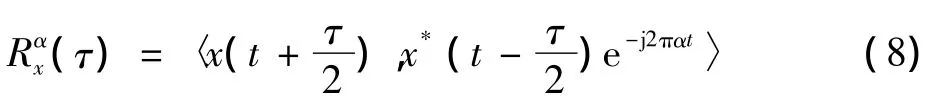
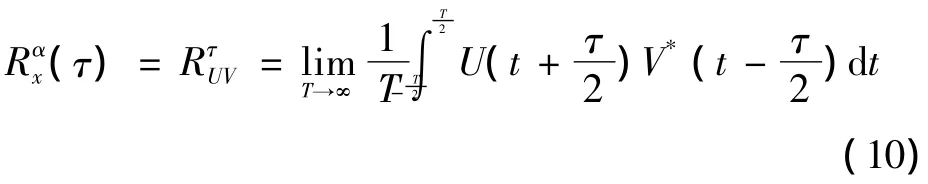
式中:U(t)=x(t)e－jπαt;V(t)=x(t)ejπαt。

式中:XT(t，f)是x(t)的短时Fourier变换;(f)称为谱相关密度函数;Δt是所取平滑窗长度。

传统MPSK信号的载频估计基于式(5)和式(11)的运算得到载频估计表达式

当M=2时，有

当M≥4时，有

式中:Q(f)=。

根据式(12)和式(13)在高信噪比时可以很好地估计出载频。当分析按时间抽选的基－2 FFT算法时会发现，在实际中为了节省计算量，FFT算法是分为前后两部分进行的。当对信号进行FFT变换时，会发现FFT变换后的图形基本上是关于中心频率对称的，但是当分析其变换后的数据时，其数据并不是对称的。因为对一个N=2l点的FFT变换时，它的后半部分是从前半部分变换得来的。

信号x(t)的N点FFT前半部分变换为

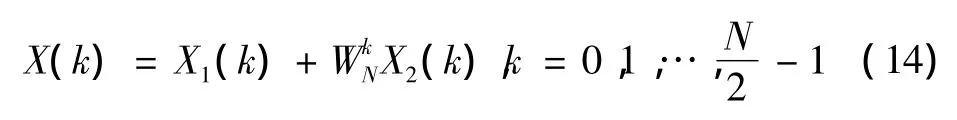
信号x(t)的N点FFT后半部分变换为

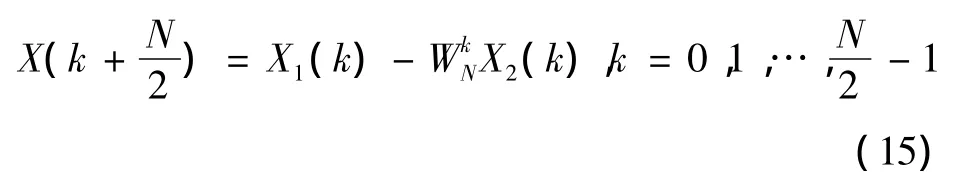
通过分析FFT变换，发现FFT变换后的前后两部分相似，它们相关度很高，可以运用互相关理论对其分析。为了充分利用前后两部分的相似性对式(11)做修改，得到

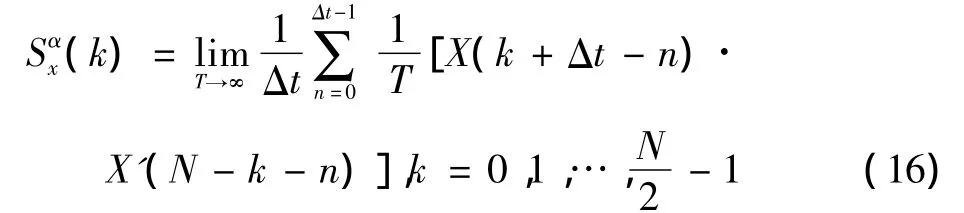
式中:X(k+Δt－n)，X'(N－k－n)分别表示x(t)经FFT后的前半部分和后半部分;α=0。

式(16)是载频粗估计的计算式，虽然是粗估计，但是准确率很高。在本文提出的算法中，因为要在高速通信中达到高分辨率和减少计算量的情况下，用式(16)作为第一级的盲估计，其载波频率为f1。

2.2 功率谱算法分析

功率谱估计载波频率是常见方法之一，但是为了满足实时高精度的要求，对采样信号进行下变频后，提出一种新的功率谱估计方法。

功率谱密度与自相关函数构成傅里叶变换对，信号的傅里叶变换用FFT来实现，利用式(6)得到功率谱密度函数为

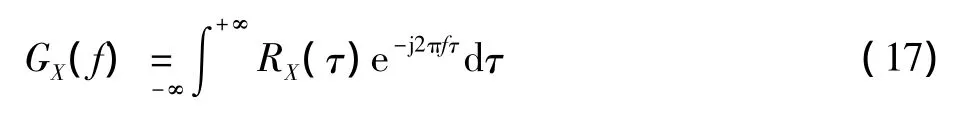
式中:RX(τ)是接收信号的自相关函数。由式(5)可以得到

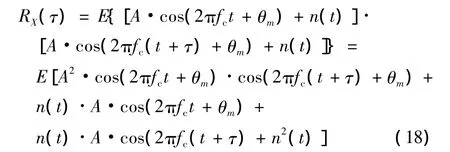
对于式(18)，令

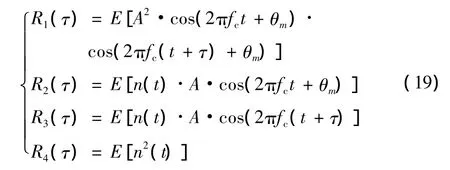
由于噪声n(t)与信号x(t)的相关性很小(理论上为零)，并且噪声的自相关理论为零则可知R2(τ)，R3(τ)，R4(τ)趋近于零。将式(18)和式(19)代入到式(17)计算可得到

通过式(20)令其等式右边的第1项到第4项分别为G1(f)，G2(f)，G3(f)和G4(f)通过计算得到

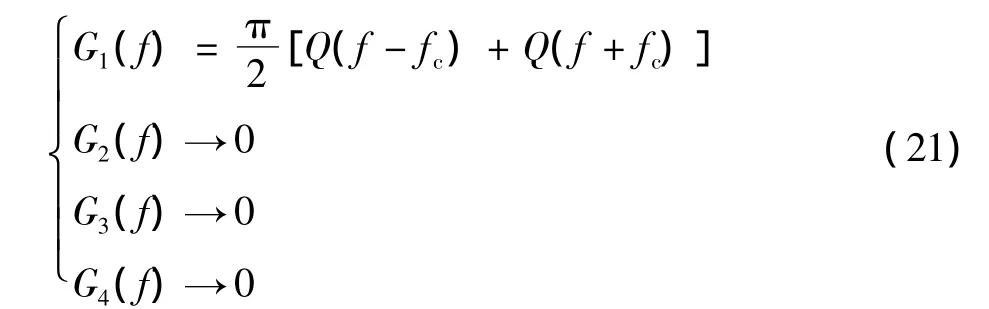
为了更好地消除噪声的影响，通过2.1节中对FFT变换的分析，这里仍然要对式(20)变换后的结果分为前后两部分作负相关，以此将G2(f)，G3(f)和G4(f)的值降到更小，来提高估计性能，得到估计频率f2。

2.3 算法流程框图

通过以上算法的分析可知整个算法的结构框图如图1所示。

图1 算法流程框图

图1中，Δf是一次载频估计后的频偏 Δf=，cos(2πf1t)是本地产生的单频信号。

算法步骤如下:

1)利用2.1节循环谱原理对接收信号进行一次载频估计，得到估计频率f1;

2)利用数字下变频原理，对接收信号下变频得到频频为Δf的信号;

3)利用2.2节功率谱估计原理，对频偏为Δf的信号进行频偏估计，得到频偏f2;

4)最后得到信号的载频为fc=f1+f2。

3 算法性能及运算量分析

3.1 算法性能分析

从式(16)可以知道平滑窗长度会影响最后的估计结果。当设定了平滑窗长度之后，FFT变换后系数的互相关长度也就确定了，它们之间成正比关系。利用信号的互相关来滤除噪声，当选取平滑窗长度很小时，小到一定长度之内，噪声也具有一定的相关度时就不能利用相关理论来滤除噪声，在低性噪比的情况下就不能实现信号的载频估计。为了对其有直观的理解，通过MATLAB仿真来验证其性能。表1是通过对BPSK调制信号的MATLAB仿真验证结果。

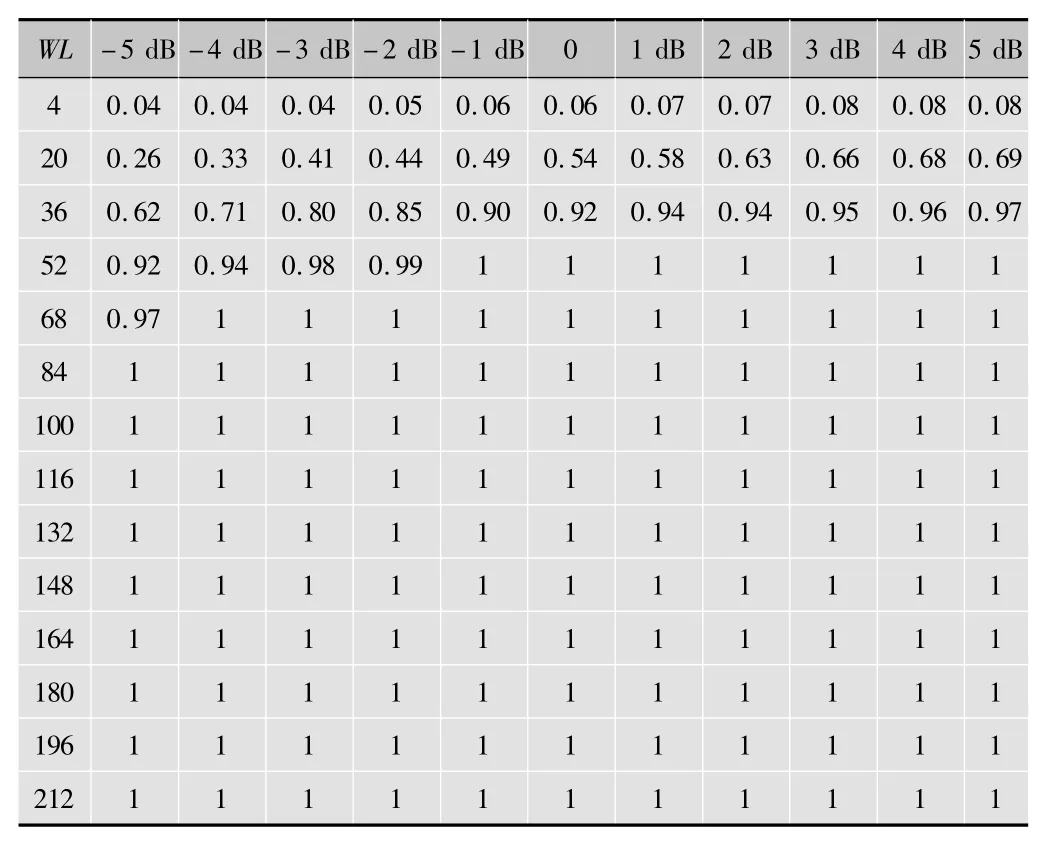
表1 BPSK调制信号载频估计的平滑窗正确率(P)分析表

表1中WL表示平滑窗长度。表1中的统计结果是在加性噪声SNR从－5 dB到5 dB，采样率为512 MHz，每一个P值是通过载频在59.375 MHz到90.507 MHz以64 kHz为步进的固定平滑窗长度和信噪比的情况下的统计结果。通过表1可知在平滑窗长度太小时估计失效，大于68点的时候估计结果完全正确。通过分析可知，平滑窗长度的选取要根据具体的环境而定，选取长度并不是越长越好。在本系统的设计中平滑窗长度选为64点。

当利用式(12)来估计载频时通过MATLAB仿真得到图2所示结果，而利用式(16)估计载频时通过MATLAB仿真得到图3所示结果。将图2和图3对比可知，将FFT后的数据分为前后两部分的估计效果要比直接对其做自相关的效果好。

图2 BPSK调制信号载频估计

图3 BPSK调制信号估计结果

图2和图3是在信噪比为－8 dB，采样频率为512 MHz，BPSK 信号载频为 3.2 MHz，采样点数为 8 192的条件下的MATLAB仿真结果。从图3可知载波频点为50，根据频率换算换算关系

式中:fs表示采样率;m表示FFT点数;f'表示所估计的频率值。

从式(22)和图3的估计值可以得到BPSK的载频为3.2 MHz，而根据图2无法得出正确的载频频率。这说明根据式(16)所得估计值更为准确。这也是采用新方法的原因之一。

一次估计的性能已经很好，但是有时候需要更高的分辨率，而又不想拥有大量的计算量，就采用两次估计及一次粗估计和一次精估计。当然分两次估计的准确率会比一次估计性能差一点，但是与采用一次估计的计算量大到无法用现有的硬件来实现比较，还是愿意采用两次估计。其计算量和性能分析将在下文说明。

3.2 计算量分析

本文提出的算法是基于循环自相关进行的。在一次估计中，首先对采样的m点数据进行FFT变换，然后将FFT变换后的数据分成前后两部分，在α=0的情况下运用自相关原理，使用频域平滑对信号进行载频估计。在二次估计中，首先对采样的下变频信号进行自相关运算，然后对采样的n点数据进行FFT变换，然后把FFT变换后的数据分成前后两部分进行互相关运算。

在一次运算中，FFT运算的乘法和加法次数分别为:mF=(m/2)·lbm和aF=mlbm，自相关运算和平滑窗运算的乘法次数和加法次数分别为:mR=m/2和aR=(m/2－L/2)·L，其中L表示平滑窗长度。在二次估计中，两次自相关的乘法次数为:m'R=2·n/2，FFT运算的乘法和加法次数分别为:mF'=(n/2)lbn和aF'=nlbn。

用一组数据来具体反应运算量的大小，比如利用本文采用的数据来分析。一次采样率为512 MHz，FFT变化点数为8 192点，平滑窗长度为64点。二次采样频率为512 kHz，FFT变换点数为8 192点。则总的乘法和加法次数分别为:118 784次和473 088次。这样的计算量如果采用Xilinx公司的V4系列的FPGA完全可以满足。

在上面的分析中提到，本算法采用了两次估计的方法来做载频估计，这是为了提高载频估计的分辨率，而运算量和运算方法又必须要满足当前硬件条件。比如本文采用的一次估计的分辨率为64 kHz，二次估计的分辨率达到64 Hz，最终分辨率为64 Hz。如果采用一次估计就要达到64 Hz，那么一次FFT变换点数就必须为8M个点，这在现有的硬件是无法实现的。

4 仿真结果及分析

为了说明仿真的正确性，在MATLAB中给出了高斯信道、多径瑞利衰落信道、多径莱斯衰落信道的仿真结果图，如图4～图6所示。

图4～图6的采样频率为512MHz，BPSK信号载频为3.2 MHz，采样FFT变换点数为8 192。高斯信道噪声为－5 dB;多径瑞利衰落信道的多普勒频偏最大值为2 kHz，多普勒频谱特性为Jakes;多径莱斯衰落信道K因子为0.5，多普勒最大频偏为2 kHz，多普勒频谱特性为Jakes。

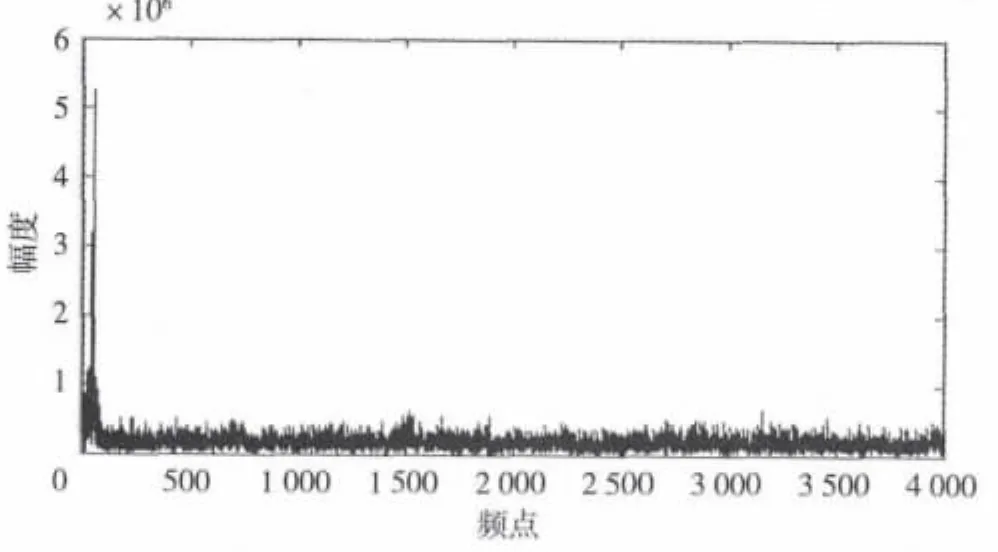
图4 高斯信道仿真

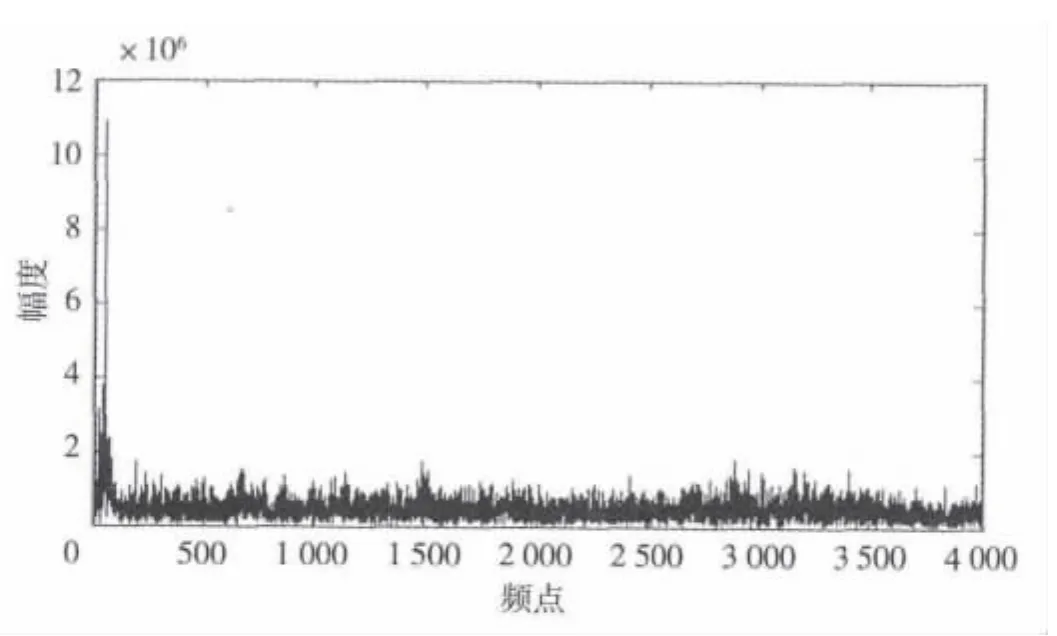
图5 多径瑞利衰落信道仿真

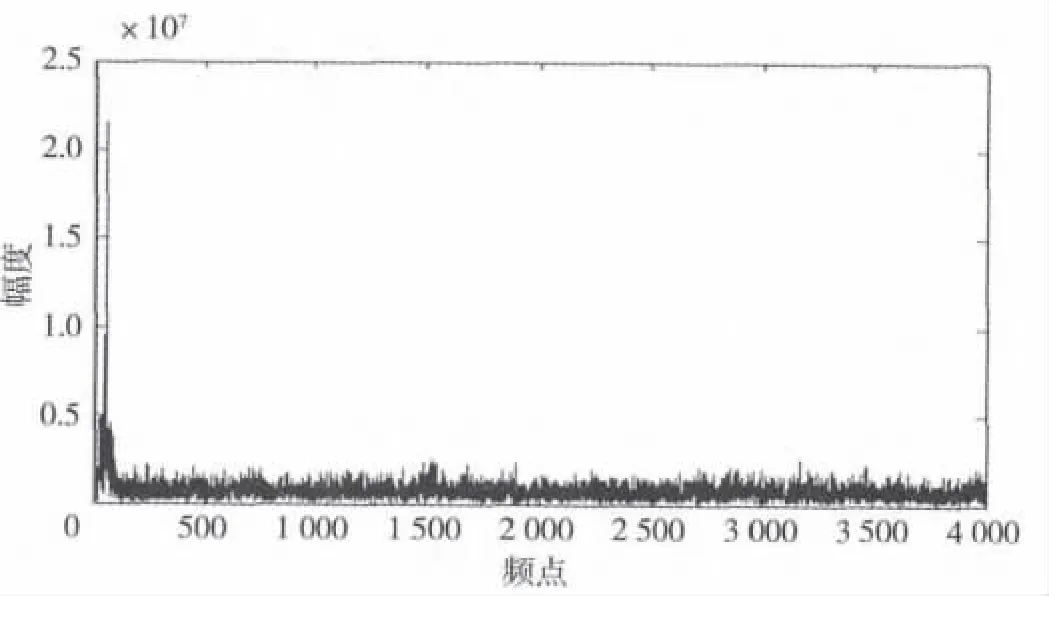
图6 多径莱斯衰落信道仿真

从式(22)和图4～图6的估计值可以计算得到BPSK的载频为3.2 MHz，仿真结果与理论相符，说明了算法的正确性。

图7和图8在以下条件下进行:符号率选取以64 kbit/s为步进从64.6 kbit/s到25 Mbit/s的变化值，载波频率选取以320 kHz为步进从323 kHz到125 MHz的变化值，一次估计的采样频率为512 MHz，一次估计的FFT变换点数为8 192点，一次估计的平滑窗长度选64点，二次估计采样率为512 kHz，二次估计的FFT变换点数为8 192点，仿真中SNR是从－5 dB到5 dB。完成了BPSK，QPSK，8PSK的载频盲估计的仿真。

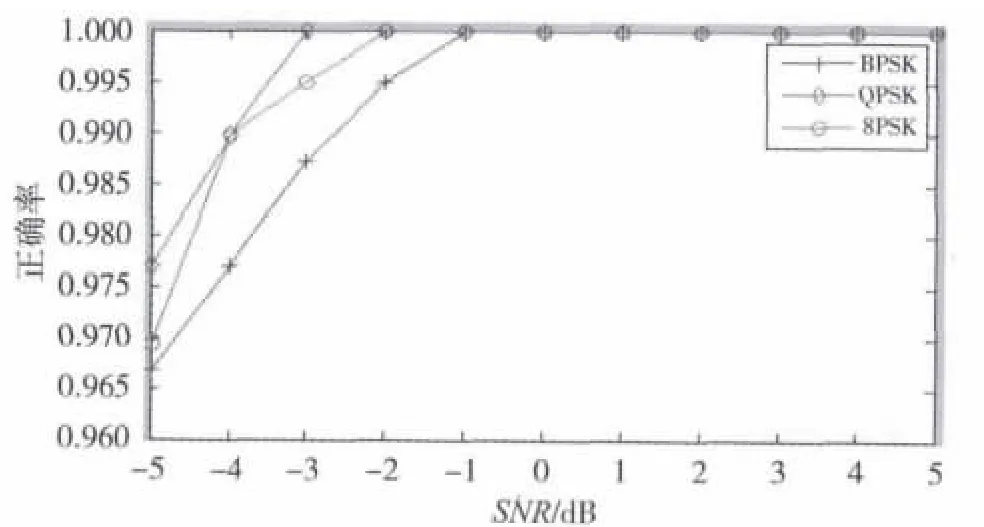
图7 一次载频估计统计结果

不难理解一次估计的准确率要比二次估计高。从统计结果可以知道当SNR=－5 dB时，一次估计方法就具有了一定的实用性。从表1可知，如果想要准确率再提高，可以加长一次估计的平滑窗长度，通过本文前面对本算法的计算量分析可知，只要平滑窗长度控制在合理的范围内，计算量还是不大，当前硬件是完全可以实现的。

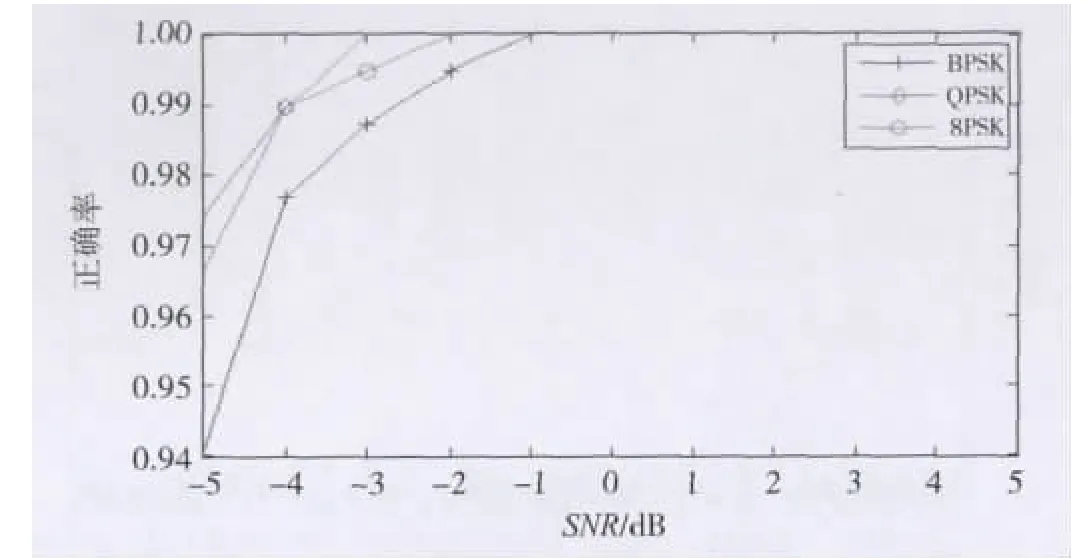
图8 二次载频估计统计结果

5 总结及展望

本文提出了一种新的MPSK盲载频估计方法，是信息提取的基础之一。通过研究FFT算法，给出其特点，并利用其特点来估计载频，将计算量降到完全可以实现的条件下。再运用自相关可以滤除噪声的特点，从而不必为滤除噪声而专门设计滤波器，从而达到易于实现的目的。通过二次估计提高了载频的估计分别率，当然在提高分辨率的同时，估计的准确率有所下降。在MPSK的载频估计中，此算法可以快速、精确地实现。当然载频估计的方法有很多，对于不同信号在不同条件下的具体应用可能还需要对算法进行优化，甚至选用其他算法，在以后的工作中还会继续对载频估计进行较为深入的研究，更好地适应现代高速和可靠的通信系统。

［1］谭舒，吕明，成昊，等.DS/BPSK信号载频估计方法的研究［J］.信息技术，2006(7):117－119.

［2］郑鹏，张鑫，刘锋.基于时域平滑循环周期图的直扩信号载频估计［J］.中国电子科学研究院学报，2011，6(5):530－532.

［3］王戈，严俊.一种基于功率谱估计的盲载频估计新算法［J］.计算机工程与应用，2012，48(13)，114－118.

［4］邓振淼，刘渝.MPSK信号载频盲估计［J］.通信学报，2007，28(2):94－100.

［5］ HARING L，BIEDER S，CZYLWIK A，et al.Estimation algorithms of multiple channels and carrier frequency offsets in application tomultiuser OFDM systems［J］.IEEE Trans.Wireless Communications，2010，9(3):865－870.

［6］ SOLIS－ESTRELLA H，OROZCO－LUGO A G.Carrier frequency offset estimation in OFDMA using digital filtering［J］.IEEEWireless Communications Letters，2013(2):199－202.

［7］ GARDNERW A，SPOONER CM.Signal interception:performance advantages of cyclic－feature detectors［J］.IEEE Trans.Communications，1992，40(1):149－159.

［8］郑鹏，张鑫，刘锋，等.窄带干扰下基于循环谱的 BPSK直扩信号盲检测［J］.电视技术，2012，36(7):78－81.

［9］ GARDNER W A，BROWN W A，CHEN C K.Spectral correlation of modulated signals:part II－digitalmodulation［J］.IEEE Trans.Communications，1987，35(6):595－601.

［10］ LIYingxiang，YIMin，YANG Qin，et al.Low SNR BPSK signal chip rate estimation using a wavelet based spectral correlation algorithm［C］//Proc.45th Midwest Symposium on Circuits and Systems.［S.l.］:IEEE Press，2002:247－249.