GPS与DTMB组合导航精度因子研究
田安红,付承彪
(曲靖师范学院计算机科学与工程学院,云南曲靖655000)
众所周知,可利用全球定位系统(GPS)来获取目标的准确位置,而位置精度大小依赖于当前时刻所观测到的GPS卫星数目多少[1],即几何精度因子(GDOP)取值大小,但单GPS定位系统也存在定位盲区现象,如在地下停车场、室内、隧道等区域,因目标接收机所获得的卫星数目少于4颗而无法完成定位,目前无线电导航定位技术发展的趋势是从单定位系统向多种组合导航定位系统转变[2],通过融合多个信号源来增强卫星数目,提高最终定位精度。
最近几年内,出现新的数字电视定位系统的定位技术,我国采用地面数字电视广播信号(DTMB)标准,当目标运动到数字电视定位系统所覆盖的范围时,可以利用广播数据帧信号的收发时间确定目标与电视塔的距离值[3],进而实现对运动目标的定位,电视塔位置固定可类似伪基站,提供所需的位置信息[4]。当DTMB与GPS联合定位时,存在两种信号源,增加了同一时刻的可见卫星数目,使得定位卫星的空间几何布局得到改善,而几何布局好的卫星计算所得几何精度因子值小,定位误差小。然而多源信号的融合涉及到不同的定位系统,国内外针对单数字电视系统定位功能有所研究,但数字电视系统与其他导航技术的融合研究较少,针对这些不足,本文重点研究组合导航系统的定位模型,以及DTMB信号的增加如何改善精度因子的大小来提高导航定位精度的问题。
1 组合定位系统
因数字电视定位系统能够依据数据帧的信息获取发射塔与接收机间的距离大小,即因DTMB定位技术可采用伪距测量来实现[5],其伪距方程表示为

式中:ρ是伪距;c是光速;tT表示电视定位系统中某个数据帧的发射时间;tR表示接收机收到该数据帧的时间;r表示电视塔与接收机间真正距离大小;δr表示测量误差大小。
在GPS定位系统中也是采用伪距测量方法,其伪距方程为

式中:r表示伪距值;(xi,yi,zi)表示GPS卫星坐标信息;c为光速;tu表示时钟偏差;(xu,yu,zu)表示接收机坐标信息。
因DTMB和GPS定位系统都可以采用伪距测量技术[6],在GPS定位盲区,可以采用DTMB定位系统来增强GPS定位技术,弥补定位盲区的缺陷,基于全球定位系统GPS与数字电视定位系统DTMB的组合导航定位系统如图1所示。
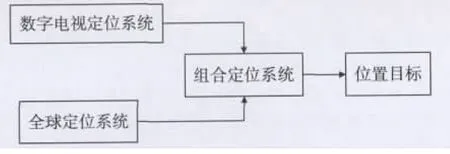
图1 组合定位系统
从图1可知,组合定位系统中存在2个不同的定位系统模型,每一个定位系统模型具有自己的时钟计算方式,因此定位未知数至少5个,即三维位置坐标和两个系统时钟偏差。其组合定位方程表示为

式中:(xi,yi,zi)为第i颗GPS卫星或DTMB电视塔的坐标信息;(xu,yu,zu)为未知的三维目标坐标信息;ρi为伪距值;b1为GPS卫星信号的钟偏移量;b2为DTMB信号的钟偏移量。如果某伪距值是GPS卫星信号,则说明只采用单独的GPS卫星信号来定位,此时k1=1,k2=0;如果某伪距值是DTMB信号,则说明只采用单独的DTMB信号来定位,此时k1=0,k2=1。
2 精度因子
在导航系统的定位精度研究中,有很多衡量定位精度的方法,如卫星仰角大小、组合卫星体积大小等,但常见的是使用几何精度因子[7]来衡量卫星的空间几何布局情况,几何精度因子推导过程如下:
从组合观测方程(3)可知,当采用最小二乘算法时所得解为

假设观测方程为

则定位误差为
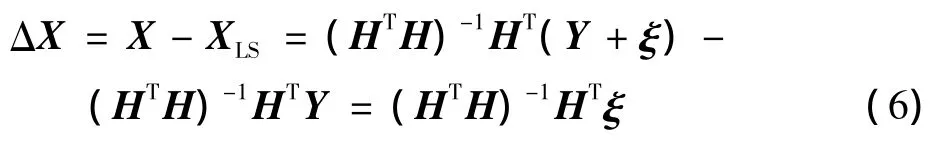
设定噪声方差为σ2,则定位误差的协方差为

从式(8)可知,总误差大小主要与几何精度因子GDOP有关。GDOP表示由卫星空间位置决定的对用户测距误差的放大程度[8],其值的大小由定位所采用的组合卫星的空间位置布局好坏决定。当采用接收机定位时,依据总定位误差表达,主要考虑选择组合卫星星座最小的GDOP值,即求解出的定位误差小[9],符合实际中定位精度小的需求。
当精度因子的参数取值不同时,按照精度因子的推导公式能够进一步求出位置精度因子、水平精度因子、垂直精度因子、接收机钟差精度因子分别表示为

3 仿真分析
组合导航定位的思想是利用两个定位系统相融合,解算出目标的位置信息,在GPS定位盲区,卫星数目少于4颗而无法单独完成定位,可采用数字电视定位系统来增强GPS,数字电视定位系统DTMB可以作为一个信号源信号,与GPS卫星一同参与定位,改善卫星的几何分布结构,减小GDOP取值,获取高精度定位结果。
为了验证数字电视系统的增加可改善单GPS定位系统的性能,本文以6颗GPS卫星信号为例,因此一共有=15种组合。GPS和DTMB电视塔的坐标信息通过测量获取,GPS和DTMB的坐标如表1所示,在表1中,卫星1~卫星6均表示GPS卫星,卫星7~卫星9表示DTMB电视塔。
为了便于分析DTMB电视塔数目的变化,对组合导航定位精度的影响,采用4种定位场景来对比分析,如图2~图6所示。
场景 1:单 GPS 卫星,用 GPSG,GPSP,GPSH,GPSV,GPST表示;

表1 坐标信息

图2 GDOP值对比效果图
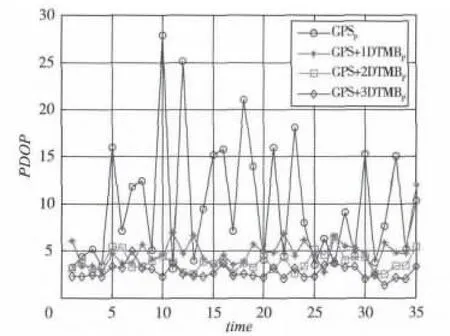
图3 PDOP值对比效果图
场景2:GPS与1个DTMB信号组合,如精度因子用GPS+1DTMBG表示;
场景3:GPS与2个DTMB信号组合,如精度因子用GPS+2DTMBG表示;

图5 VDOP值对比效果图
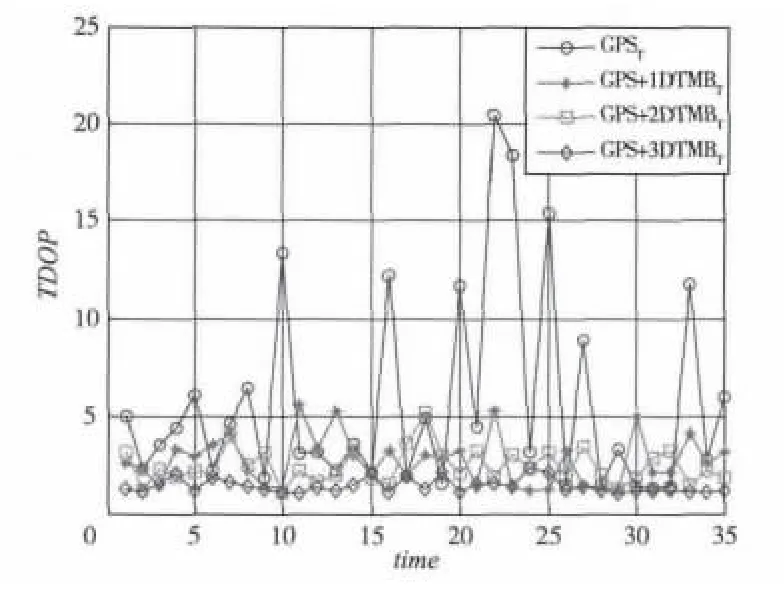
图6 TDOP值对比效果图
场景4:GPS与3个DTMB信号组合,如精度因子用GPS+3DTMBG表示。
从图2中知,在15次的组合卫星中,对每种组合下的精度因子仿真对比分析,发现基本上趋向于这样的规律,即GPSG<GPS+1DTMBG<GPS+2DTMBG<GPS+3DTMBG,说明当DTMB信号源增多时,几何精度因子逐渐变小,且从图2中可以得出,在接收机只接收到GPS卫星时,几何精度因子基本上都在8 m左右变化,且某组合时刻下,如16时刻几何精度因子达到25m,在27时刻达到16 m,即表明在某些组合下,卫星在空中的布局不好,导致几何精度因子变化很大,从而限制了单独GPS定位系统在高精度范围的应用。而新增一个信号源DTMB后,几何精度因子在5 m左右变化,曲线波动范围变小,当增加2个DTMB信号源和3个DTMB信号源后,曲线变化更加平滑。
而在相同组合下的位置精度因子、水平精度因子、垂直精度因子和接收机钟差因子的仿真结果如图3~图6所示。
从图3~图6可以看出,不同精度因子的曲线变化规律也大致相同,即GPSP<GPS+1DTMBP<GPS+2DTMBP<GPS+3DTMBP,GPSH<GPS+1DTMBH<GPS+2DTMBH<GPS+3DTMBH,GPSV<GPS+1DTMBV<GPS+2DTMBV<GPS+3DTMBV,GPST<GPS+1DTMBT<GPS+2DTMBT<GPS+3DTMBT,在接收机端只有GPS卫星时,不同精度因子的取值较大,某些时刻波动很大,说明卫星在这些时刻下的空间几何结构布局不好,而当增加一个DTMB信号源后,不同精度因子的取值变小,波动变小,尤其是当增加2个DTMB信号源和3个DTMB信号源后,不同精度因子的变化曲线更加平滑,从而也证明了组合定位数目增多时,精度因子变小,且精度因子取值满足实际定位的需求。
4 总结
在单定位系统逐渐向多定位系统融合趋势的发展之下,利用数字电视定位系统已有的优势,给出GPS与DTMB组合定位思想,并针对多系统下导航精度的计算问题,研究精度因子大小,通过4种不同的仿真环境来验证不同信号源组合下的精度因子大小与定位精度的关系,仿真结果表明随着DTMB信号源的增加,精度因子变化曲线更加平滑,当DTMB信号源增加到2个时,精度因子取值在3 m左右,可以满足实际需求。
[1]陈灿辉,张晓林.卫星定位和精度因子的改进方法[J].北京航空航天大学学报,2011,37(4):472-477.
[2]蔡成林,李孝辉,吴海涛.混合星座的精度因子与定位性能分析[J].测绘科学,2009,34(2):67-69.
[3] MOON G B,JEE G I,LEE JG.Position determination using the DTV segment sync signal[J].International Journal of Control,Automation and Systems,2011,9(3):574-580.
[4]丁涛.NLOS环境下基于DTV信号的定位算法研究[D].南京:东南大学,2010.
[5]田安红,周非,付承彪.TV-GPS技术融合实现无缝定位分析[J].电视技术,2009,33(8):54-56.
[6]李雯琦,吴虹,张南,等.地面数字电视信号与GPS相结合的定位系统[J].电视技术,2010,34(6):11-15.
[7]王梦丽,孙广富,王飞雪,等.混合星座导航系统的加权几何精度因子分析[J].中国空间科学技术,2007(5):50-55.
[8]陈小平,滕云龙,康荣雷,等.几何精度因子改进算法研究[J].电子科技大学学报,2008(S1):27-30.
[9]金玲,黄智刚.多卫星组合系统的快速选星算法研究[J].电子学报,2009,37(9):1931-1936.

