基于转静子耦合的组合压气机动力特性分析

漆文凯，王向辉

（南京航空航天大学能源与动力学院，南京210016）

0 引言

随着航空技术的不断发展，现代航空发动机的设计转速越来越高，相应地机匣壁则设计得越来越薄，从而使发动机转子、支承以及机匣之间的相互耦合日益加强，形成了复杂的结构动力特性。目前研究旋转机械动力特性的方法主要有2大类，即传递矩阵法和有限元法。传递矩阵法因为编程简单、计算速度快且有效而被广泛应用[1-5]。随着计算机技术的跨越式发展，大型商用有限元软件的开发和不断完善，有限元法以其计算精度高、数值稳定的特点，被越来越多的研究者所采用[6-9]。国内外已有很多学者对航空发动机转子系统的动力特性进行了深入研究[1-9]，但考虑机匣与转子耦合的研究还相对较少。文献[10]基于NASTRAN中实体单元编制的转子动力特性计算程序，对发动机整机进行了动力特性计算，并研究了考虑机匣振动耦合时转子系统临界转速的确定方法；文献[11]分别运用静刚度、动刚度和整机有限元模型对某型发动机进行了转子动力特性计算，并指出运用整机模型能够充分考虑支承动刚度和各种机匣的局部振动对整机振动的影响；文献[12]建立了1种新型的转子-滚动轴承-机匣耦合动力学模型，利用数值积分方法获取了系统响应，并研究了航空发动机的整机振动规律；文献[13]针对实际的双转子航空发动机，建立了发动机双转子-支承-机匣耦合动力学模型，运用数值积分方法获取系统非线性振动响应，研究耦合系统的动力特性。

本文以组合压气机为研究对象，考虑了转子-支承-机匣系统的耦合效应，采用3维实体单元建模，利用有限元分析软件ANSYS，对组合压气机进行动力特性分析。

1 组合压气机建模

由转子动力学[14]可知，1个旋转机械系统的运动微分方程式为

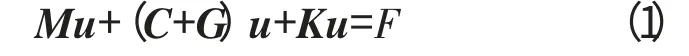
式中：M 为系统质量矩阵；C 为系统阻尼矩阵；G 为系统陀螺矩阵；K 为系统的刚度矩阵；u 为系统的位移响应矢量；F 为系统所受载荷；C，G 和u 分别为转速的函数。

该方程的特征解和特征向量对应系统的固有频率和振型，当转速与系统的固有频率相等时，该转速即为系统的临界转速。

利用3维实体建模软件UG建立机匣厚度为5、3和2mm的组合压气机模实体型，机匣厚度为3mm的组合压气机转子模型和部件模型分别如图1、2所示。

图1 组合压气机转子模型

图2 组合压气机模型

该压气机由2级轴流式叶轮和1级离心式叶轮组成。在实体模型的基础上，可以建立组合压气机转子-支承系统(RBS)和转子-支承-机匣系统(RBCS)的有限元模型，分别如图3、4所示。其中，实体单元采用SOLID185单元，而支承部分则采用CONBINE14单元模拟，模型详细参数见表1。

图3 转子-支承系统的有限元模型

图4 转子-支承-机匣系统有限元模型

2 转子-支承系统动力特性分析

旋转机械有1种特有的现象，即在转速增大到某些特定转速时，转子的挠度会迅速增大，而当转速超过该转速时，挠度又迅速减小，这些特定的转速称为其临界转速。利用有限元分析软件ANSYS对建立的组合压气机转子-支承系统进行动力特性分析，绘制了该系统的Campbell图，如图5所示，并得到其前3阶临界转速，见表2。由于同阶正、反进动的振型一致，这里仅列出前3阶正进动时的振型，分别如图6~8所示。

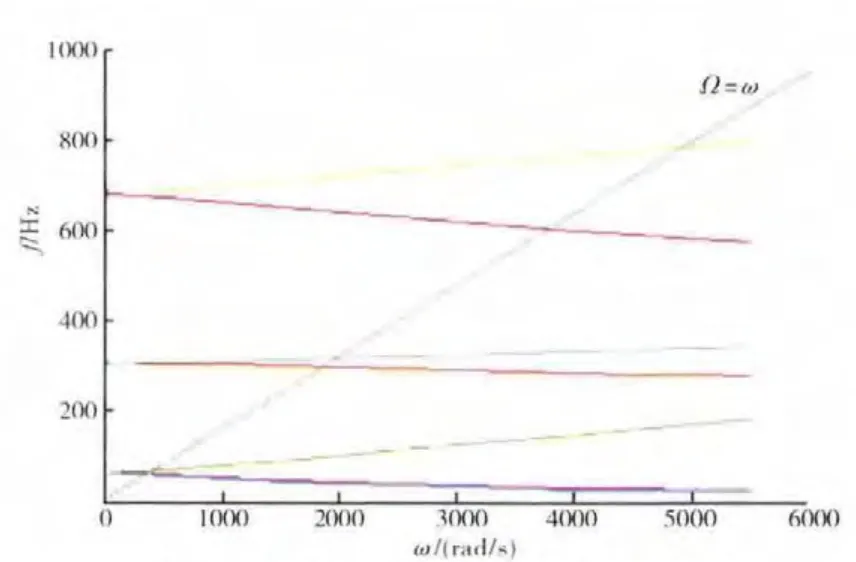
图5 转子-支承系统的Campbell

表2 转子-支承系统的临界转速 rad/s

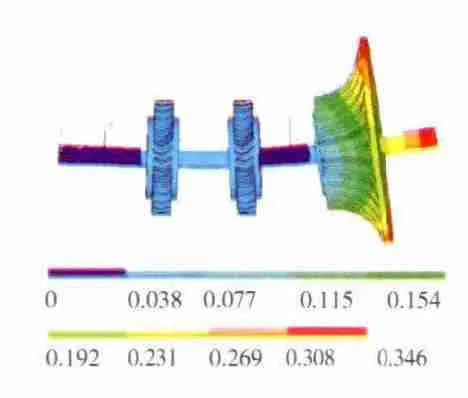
图6 转子-支承系统第1阶正进动振型

图7 转子-支承系统第2阶正进动振型

3 机匣部件模态分析

航空发动机机匣作为发动机的承力机构，发挥着传递转子载荷、包容转子的重要作用，随着机匣部件的日趋薄壁化，其振动特性也越来越复杂。现对厚度分别为5、3和2mm的组合压气机机匣部件进行模态分析，通过ANSYS软件计算机匣部件前5阶固有模态，得到其固有频率及固有振型，其频率见表3，由于3个模型的振型相同，限于篇幅，仅列出厚3mm的机匣部件的前5阶固有振型，分别如图9~13所示。

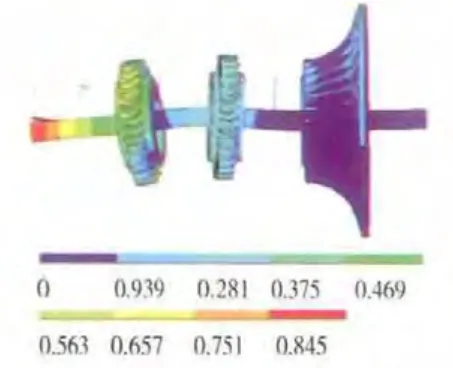
图8 转子-支承系统第3阶正进动振型

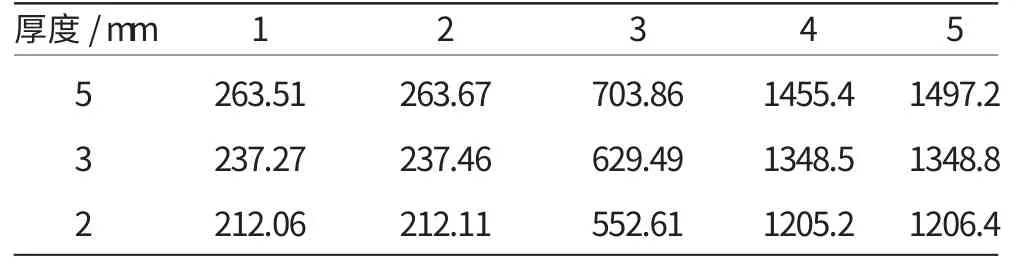
表3 组合压气机机匣前5阶固有频率 Hz

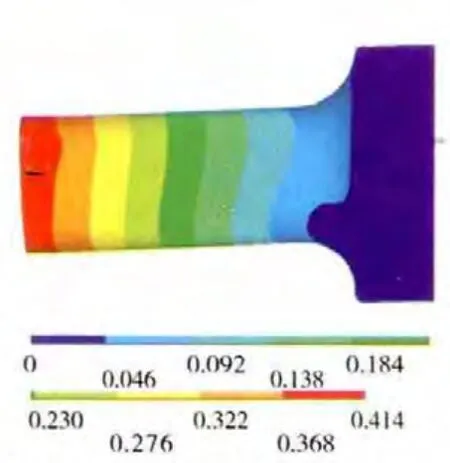
图9 组合压气机机匣第1阶振型

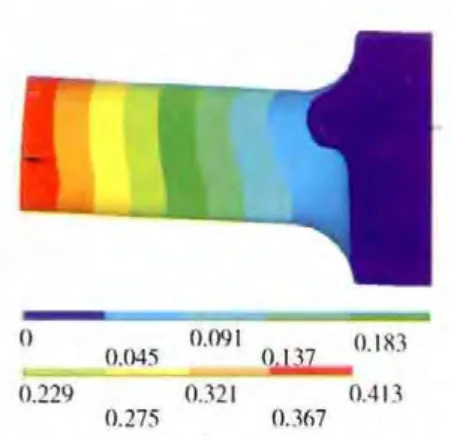
图10 组合压气机机匣第2阶振型

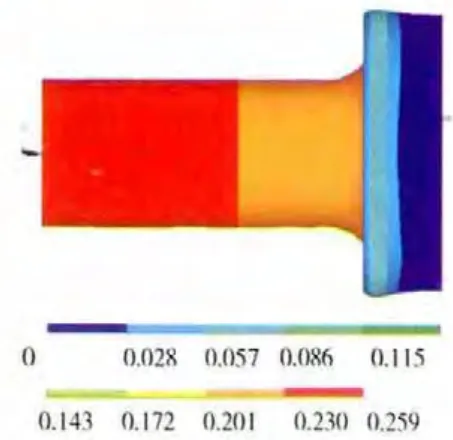
图11 组合压气机机匣第3阶振型

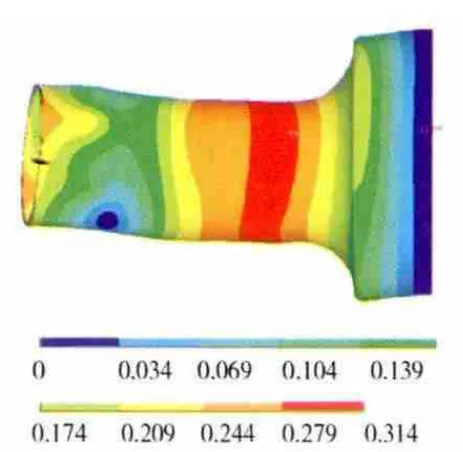
图12 组合压气机机匣第4阶振型

结合表3以及对应频率的振型图可见，第1、2阶模态是机匣部件Z、Y 方向振动的第1阶弯曲振动，第4、5阶模态是机匣部件的第2阶弯曲振动，而第3阶模态则是机匣轴向伸缩振动。同时，从表3中可见，机匣部件的各阶固有频率随着机匣厚度的减小而降低。

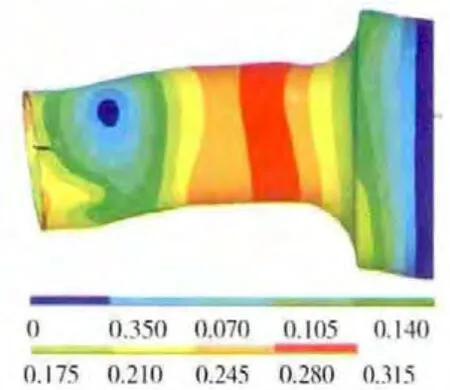
图13 组合压气机机匣第5阶振型

4 转子-支承-机匣系统动力特性分析

机匣厚度的减小，其抗弯刚度也随之降低，这对转子系统的动力特性将产生很大影响。本文利用ANSYS软件分别计算了机匣厚度为5、3、和2mm的组合压气机系统的前4阶临界转速，并将其与转子-支承系统的临界转速（同一转子振型）对比，见表4，同时得到了对应转速下的振型。限于篇幅，在此仅列出机匣厚度为3mm的组合压气机系统的正进动振型，分别如图14~17所示。转子-机匣系统也应给出Campbell，转子-支承-机匣（3mm）系统Campbell如图18所示。

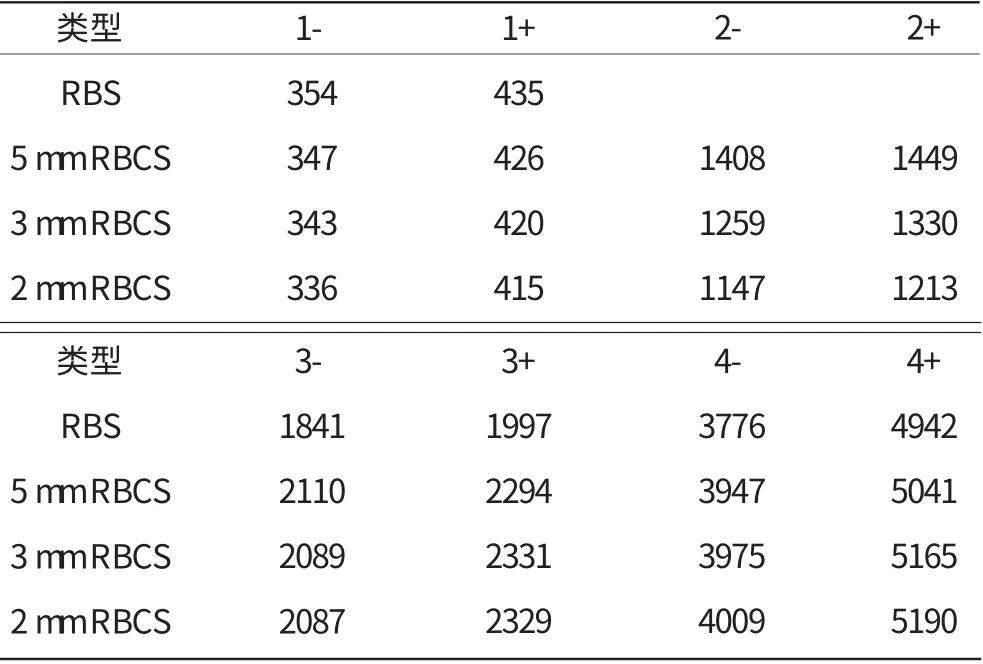
表4 转子-支承系统(RBS)与转子-支承-机匣系统(RBCS)前4阶临界转速 rad/s

图14 转子-支承-机匣系统第1阶振型

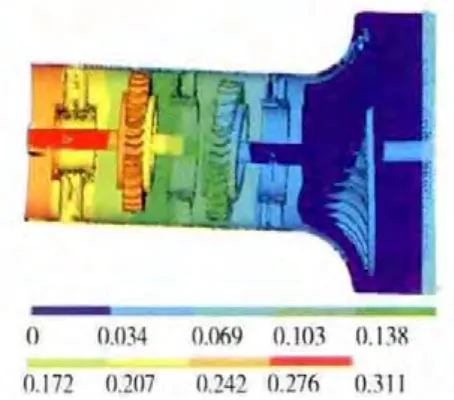
图15 转子-支承-机匣系统第2阶振型

图16 转子-支承-机匣系统第3阶振型

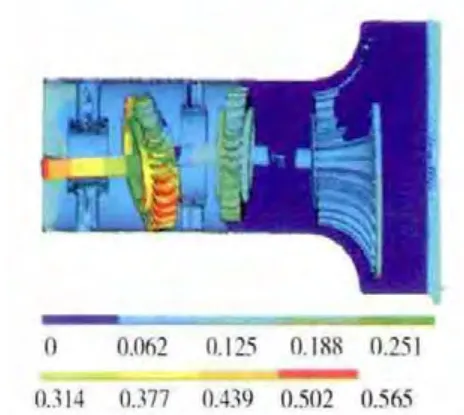
图17 转子-支承-机匣系统第4阶振型

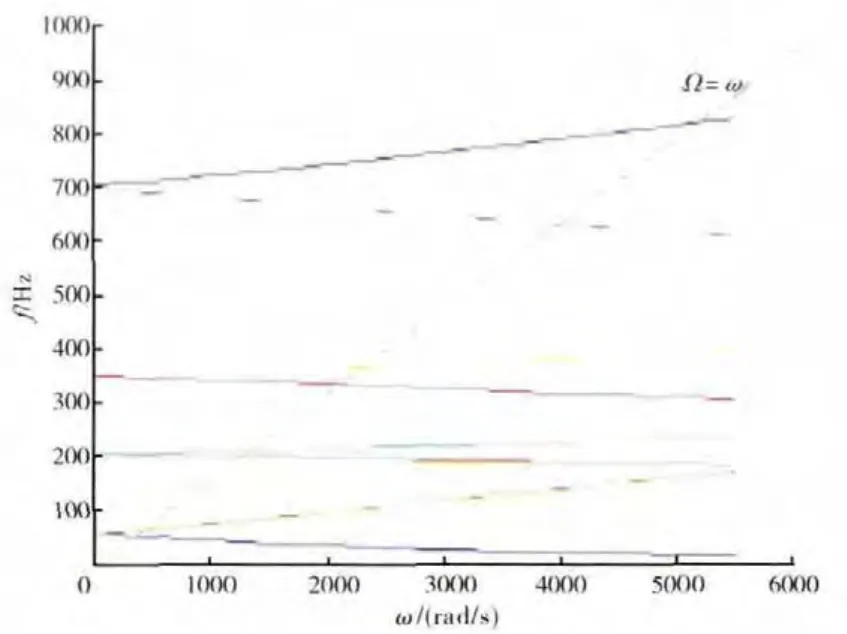
图18 3mmRBCScampbell

从表4中可见，各组合压气机系统的第2阶临界转速和机匣第1阶固有频率均随机匣厚度的减小而降低，且其临界转速也比对应的机匣第1阶固有频率有所下降。

5 不平衡响应分析

不平衡响应分析是旋转机械系统动力特性分析的重要部分，可以预测转子系统在某些工况下的振动情况，还可确定转子在计及阻尼影响时的临界转速[15]。本文利用ANSYS软件对机匣厚度为3mm的组合压气机模型进行不平衡响应分析，从而验证计算所得临界转速正确与否。在第1级轴流式轮盘施加5g·mm的不平衡量，阻尼比为0.01，在转子转速为600~60000r/min范围内，计算位于静子部件上的前、后支承点处的振动响应，在对数变换下，其响应值随转速变化的曲线如图19所示。

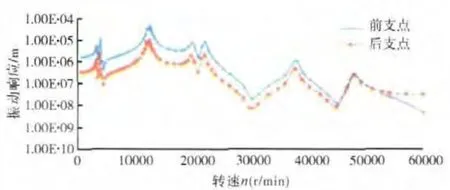
图19 机匣前、后支点振动响应随转速变化曲线

从图19中可见，其响应值在8个转速值处达到峰值，将该峰值转速与上文计算所得临界转速进行对比，其结果见表5。

从表5中可见，机匣前、后支点的振动响应峰值转速与计算所得系统临界转速误差很小，验证了计算所得临界转速值的正确性。

6 结论

（1）组合压气机转子-支承-机匣系统的各阶临界转速低于对应的转子-支承系统的临界转速，且出现了以机匣弯曲振动为主振型的临界转速。

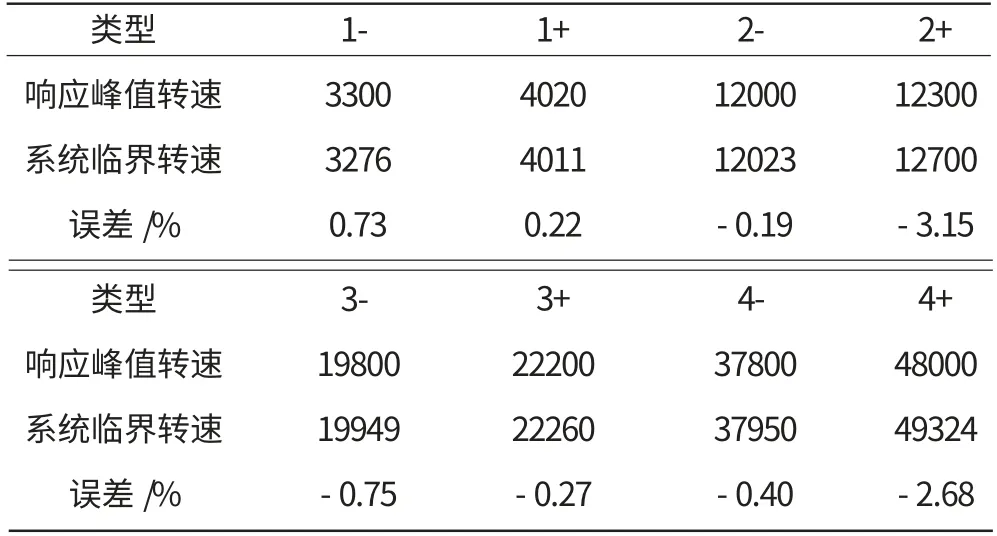
表5 支点振动响应峰值转速与系统临界转速对比 r/min

（2）随着机匣厚度的减小，组合压气机机匣部件的固有频率随之下降，而其转子-支承-机匣系统的第1、2阶临界转速也随之下降，第4阶临界转速则随之升高。

（3）组合压气机机匣前后支点的振动响应峰值转速与系统临界转速值相吻合，验证了临界转速的正确性。

[1]Prohl M A.A general method of calculating critical speeds of flexible rotors[J].ASME,1945（67）：142-146.

[2]Gunter E J.Unbalance response of a two spool gas turbine engine with squeeze film bearings[R].ASME 81-GT-219.

[3]Gunter E J.Design of nonlinear squeeze-film dampers for aircraft engines[J].Journal of Lubrication Technology，1999（1）：57-64.

[4]Kazao Y，Gunter E J.Dynamics of multi-spool gas turbines using the matrix transfer method applications[J].International Journal of Turbo and Jet Engines,1990（6）：143-152.

[5]赵明，魏德明，任平珍，等.模态综合法计算双转子临界转速研究[J].燃气涡轮试验与研究，2003，16（3）：38-41.ZHAO Ming，WEI Deming，REN Pingzhen，et al.Study of twin-rotor critical speed by mode synthesis[J].Gas Turbine Experiment and Research，2003，16（3）：38-41.(in Chinese)

[6]张谦，曹磊.基于ANSYS的临界转速计算[J].振动工程学报，2004，17（Sl）：234-237.ZHANG Qian，CAO Lei.Critical speed analysis based on ANSYS[J].Journal of Vibration Engineering，2004，17（S1）：234-237.(in Chinese)

[7]Chiang H W,Hsu C N,Tu S H.Rotor-bearing analysis for turbomachinery single and dual rotor systems[J].Journal of Propulsion and Power，2004，20（6）：1096-1104.

[8]Wei H,Chiang D，Hsu CN.Turbomachinery dual rotor bearing system analysis[R].ASME 2002-GT-30315.

[9]陈萌，洪杰，朱彬，等.基于实体单元的转子动力特性计算方法[J].北京航空航天大学学报，2007，33（1）：10-13.CHEN Meng，HONG Jie，ZHU Bin，et al.Rotor dynamic anal ysis based on solid element[J].Journal of Beihang University，2007，33（1）：10-13.(in Chinese)

[10]陈萌，马艳红，刘书国，等.航空发动机整机有限元模型转子动力学分析[J].北京航空航天大学学报，2007，33（9）：1013-1016.CHEN Meng，MA Yanhong，LIU Shuguo，et al.Rotor dynamic analysis of whole aero engine models based on finite flement method[J].Journal of Beihang University，2007，33（9）：1013-1016.(in Chinese)

[11]洪杰，王华，肖大为，等.转子支承动刚度对转子动力特性的影响分析[J].航空发动机，2008，34（1）：23-27.HONG Jie，WANG Hua，XIAO Dawei，et al.Effects of dynamic stiffness of rotor bearing on rotor dynamic characteristics[J].Aeroengine，2008，34（1）：23-27.(in Chinese)

[12]Chen G.A new rotor ball bearing stator coupling dynamic model for whole aeroengine vibration[J].Journal of Vibration and Acoustics，2009，131（6）：061009-1-061009-9.

[13]陈果.双转子航空发动机整机振动建模与分析[J].振动工程学报，2011，24（6）：619-632.CHEN Guo.Vibration modeling and analysis for dual rotor aeroengine[J].Journal of Vibration Engineering，2011，24（6）：619-632.(in Chinese)

[14]钟一鄂，何衍宗，王正.转子动力学[M].北京：清华大学出版社，1987：143-194.ZONG Yi’e,HE Yanzong,WANG Zheng.Rotor dynamics[M].Beijing:Tsinghua University Press,1987,143-194.(in Chinese)

[15]顾家柳，丁奎元，刘启洲，等.转子动力学[M].北京：国防工业出版社，1985：59-94.GU Jialiu,DING Kuiyuan,LIU Qizhou,et al.Rotor dynamics[M].Beijing:National Defence Industry Press,1985:59-94.(in Chinese)