基于外观统计特征融合的人体目标再识别

曾明勇吴泽民田 畅付 毅揭斐然

①(解放军理工大学通信工程学院 南京 210007)②(中国航空工业集团光电控制技术重点实验室 洛阳 417009)

1 引言

近年来，人体目标再识别技术得到了广泛的研究和应用，在视频网络监控、多目标跟踪等方面发挥了重要作用[1]。2013年Google公司推出的可穿戴计算设备Google Glass[2]已具备人体再识别功能，它通过眼镜的高清摄像头，可从超市等场所迅速识别出想要寻找的目标。人体目标再识别是指利用已经存在的人体目标图库，在场景或时间变化时，通过搜索图库，再次识别和确认当前所查询人体图片的目标身份[3]。由于存在光照、视角、姿态、背景和遮挡等极具挑战性的影响因素，人体再识别并不是一个简单的问题。

目前，人体再识别技术主要从3个方面来提高再识别率。第1类只采用基于图像外观特征的方法；第2类结合图像序列的空时关系进行推理；第3类结合生物特征，如人脸识别或步态识别。基于外观的人体再识别对先验知识要求最少，是本文的研究重点。外观方法目前主要存在两种不同的解决思路：(1)特征类方法，从外观特征出发，选取或设计类内具有一定不变性且类间具有较强区分性的描述特征；(2)测度类方法，从特征相似度或距离出发，在人为选择特征的基础上，有监督地学习和训练距离测度或分类器，使同类样本距离小而非同类样本距离大。此外，根据每个人在目标图库的图片数量为单帧或多帧，人体再识别还可分为单帧模式和多帧模式，多帧模式通过融合同一个人的多幅图像能够获得更好的性能。

在特征方面，人体再识别主要使用的特征有颜色、结构、形状、梯度、纹理、关键点以及区域描述子等。特征提取前可能进行前景分割、人体部件检测等预处理过程，提取到的不同特征通常可以进行级联或组合，形成区分性更强的特征。SDALF方法[3]提取前景后将人体目标分割为头部、躯干和腿部，并使用加权HSV直方图、最大稳定颜色区域和重复纹理块3种特征进行组合识别。CPS方法[4]利用人体结构检测出人体的详细部位后再进行识别。AHPE方法[5]将人体分为上下身并计算多帧模式下的产生式缩影特征。eLDFV方法[6]使用Fisher向量编码图像的亮度和梯度信息，并和 SDALF方法进行组合。文献[7]融合了方向梯度直方图和空间颜色直方图等多种特征。SCEFA方法[8]采用分层加权的HSV直方图和双向匹配的颜色区域特征，并用Gabor纹理模式描述检测到的关键点。文献[9,10]采用区域协方差的方式融合多种特征，SCR方法[9]在人体各部位上计算协方差， MRCG 方法[10]在多帧模式下计算均值协方差。此外，部分文献通过寻找人体特性或显著性进行再识别，eSDC方法[11]通过非监督的学习方式寻找个体显著特征，并和 SDALF方法进行组合增强。

在距离测度方面，测度学习的本质是在计算特征向量距离时估计各分量距离的尺度或权重，选取或突出那些区分性强的特征分量。ELF方法[12]通过AdaBoost分类器选取颜色和纹理特征。COSMATI方法[13]在协方差测度空间利用相关性选择显著区域和外观特征。ERSVM 方法[14]采用基于相对距离排序的SVM分类器集成多个特征向量权重。文献[15]采用多核 SVM 学习的方法融合颜色和视觉单词直方图。其它方法主要学习基于对称半正定矩阵的马氏测度，如采用大边近邻分类器的LMNN-R方法[16]和采用相对距离比较的PRDC方法[17]。LF方法[18]则先对高维特征进行PCA降维，再基于局部Fisher判别分析进行降维映射，获得了非常高的识别性能。

与特征类方法相比，测度学习方法对特征的选择要求较低，通常能取得更好的再识别效果。但其训练的时间和空间复杂度较高，在训练样本不足时存在过度拟合等现象，且场景和图库变化时需要重新训练。特征类方法则需要人为地寻找和设计较好的特征，方法的性能依赖于特征的优劣程度。本文在特征类方法的思路下设计和构造优秀的特征及描述，同时也讨论特征的非学习距离测度，突出方法的实用性。本文主要基于颜色和结构信息，融合两种外观统计特征描述方法进行人体再识别。此外，本文从应用的角度设计了更合理的再识别性能评估指标。最后本文在两个公共图库上进行了广泛的实验，验证本文方法的优异性能。

2 融合外观特征

本文主要基于颜色和结构信息提出了两种外观统计特征提取方法。第1种是基于多种颜色通道的空间直方图特征(Multi-Channel based Spatio-Histogram, MCSH)，第2种是融合多种颜色和梯度信息的金字塔型协方差特征(Multi-Statistics on Pyramid of Covariance, MSPC)。两种方法均不需要进行前景分割和部件检测，均在图像多个层次或区域上计算统计特征并级联成特征向量，距离测度采用简单的非监督1l测度。本文融合这两种不同的统计方式进行人体再识别，融合方法记为 HSCD(Hybrid Spatiogram and Covariance Descriptor)。

通常，人体再识别假设人在短时间内着装相同，因此颜色是人体识别最常用且最有效的特征。另外人体作为一种特殊的目标，人体结构对于人体识别也非常重要，将人体图片进行合理的多层次多区域划分能更好地反映出人体的结构信息。由于空间直方图和区域协方差都能有效地统计和融合区域内的多种信息，本文基于上述出发点探讨和设计相应的统计特征及距离测度，并将这两种基于类似特征但统计方式截然不同的方法进行融合，下面分别详细介绍。

2.1 多通道空间直方图(MCSH)

颜色直方图能够表现目标区域的整体特征，对视角和形状变化具有一定的不变性，但由于它完全忽略了颜色的空间结构，降低了模型的分辨能力。空间直方图可将颜色直方图和高阶的空间矩进行结合，因此具有更强的描述能力[19]。

2.1.1空间直方图 图像区域I的二阶空间直方图可表示为

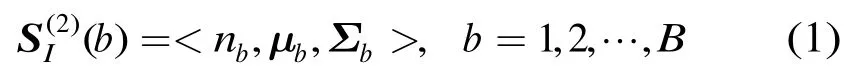
其中，B为量化级数，bn为颜色直方图，和分别为均值矢量和协方差矩阵，分别定义为

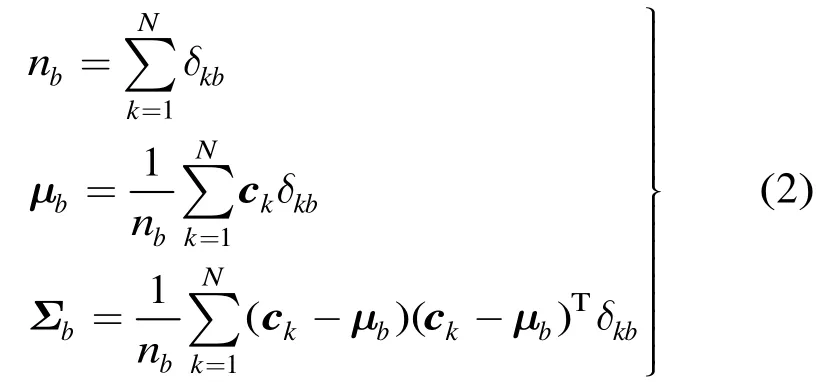
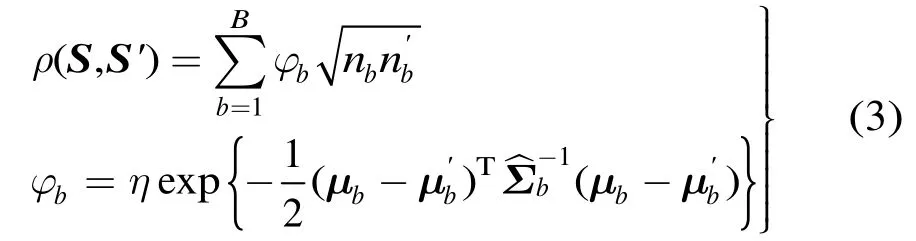
2.1.2 多通道多区域级联的空间直方图 传统的空间直方图通常在图片全局区域采用单类颜色空间进行计算，本文针对人体再识别的特定应用对其做出适当改造和增强。在区域方面采用多层次多尺度的统计区域，在像素特征方面引入描述各个区域的多种颜色通道，力求更准确地反映人体的颜色和结构信息。

通常人体检测技术获取的人体图像并不完全准确，即使对于准确的检测结果，由于检测时使用矩形框来截取人体目标，仍然会存在一定的背景干扰。另外运动人体的手脚等边缘图像信息也不一定能为识别带来好处，因此本文只采用图片的中间部分作为第1层的人体区域。其它层次的区域采用重叠或非重叠的方式进行密集型划分，并采用不同的空间直方图量化级数。以VIPeR图库[1]的图片为例，详细的分层区域划分如图1所示，图中从左至右依次为原图、网格划分图以及自顶向下的4层区域划分。其中第3层采用重叠型密集划分，4层划分中每个区域进行直方图统计的量化级数分别设为32, 32, 16和8。

在像素统计特征方面，本文除了使用常用的HSV颜色空间，还使用包含色差通道的YCbCr颜色空间以及可消除光照影响的归一化 RGB颜色空间。其中，HSV和YCbCr空间直接由第1层区域的原始RGB空间转换得到。为了进一步消除光照影响，提取归一化RGB空间前先对原始RGB空间的3个通道进行直方图均衡，再按照式(4)的定义进行计算。

图1 MCSH方法分层区域划分

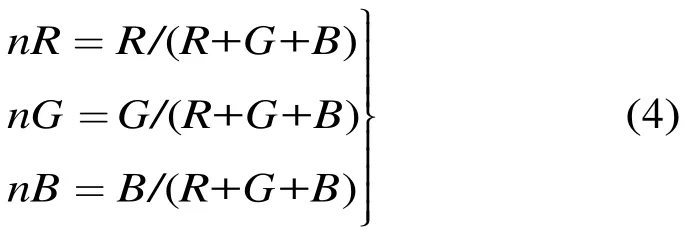
颜色通道中Y和V均表示亮度，本文只选用Y通道，在计算 Y通道时采用直方图均衡后的 RGB空间进行亮度转换。这样3种颜色空间共选出8个颜色通道。每个通道都在图 1所示的各层区域上提取空间直方图并进行级联，8个通道再依次级联形成总量化级数为2432的空间直方图S。

2.1.3 MCSH 特征优化和测度选取 获取空间直方图S后，测度的选取十分重要。采用式(3)测度的最大问题是计算复杂，存在大量矩阵求逆运算，且部分矩阵可能不可逆。从实验效果来看，式(3)空间相似度的引入也并没能显著地提升直方图的性能(参见本文4.1.1节)。

在实际场景中，尽管摄像机拍摄人体图片时可能存在较大的视角差异，但摄像机一般都位于与人体高度相当或略高的水平面上。因此，利用空间信息时可以去掉图像的水平空间信息，只保留图像的垂直空间信息。故本文将式(1)改为

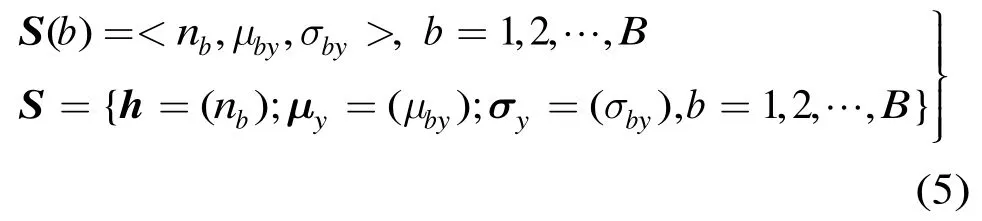
通过去除性能较差的水平空间信息，特征的提取速度和存储空间都得到了优化。对特征优化后的空间直方图S，本文将其测度设计为所含3类特征向量1l距离的加权组合

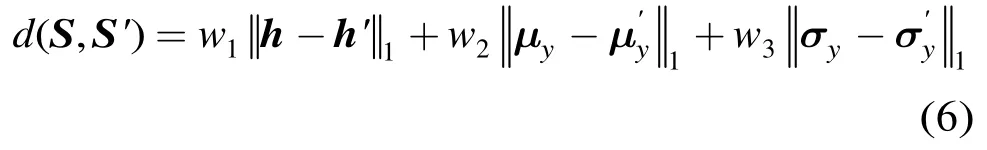
2.2 多统计性金字塔协方差(MSPC)

协方差描述子是一种与直方图截然不同的统计描述子，它通过计算图像区域内多种特征的协方差矩阵来融合多种特征[20]。本节基于上节对人体再识别的若干认识，使用协方差替换空间直方图对区域进行统计描述，区域采用多层金字塔型区域，像素特征添加梯度信息。

2.2.1协方差特征提取 本文 MSPC特征提取时同样采用多层多区域统计模式，采用金字塔型统计区域。以iLIDS图库[21]的图片为例，详细分层区域如图2所示，图中从左到右依次为原图、网格划分图以及3层金字塔型区域划分。

图2 MSPC方法分层区域划分

在图2中需要计算每个区域的协方差矩阵。对于某个图像区域R，其协方差矩阵可计算为[20]

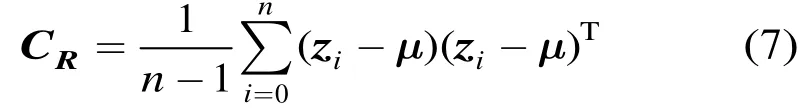
其中，n为区域的总像素，iz为使用映射函数F从区域第i个像素提取的d维特征向量，为区域均值特征向量。本文采用的像素特征映射函数F为

其中，y为像素点的垂直空间坐标，采用的颜色通道与2.1.2节相同(此处去除冗余的nB颜色通道)，后面添加的 4个特征分别为亮度通道在x和y方向上的一阶二阶梯度。

2.2.2 协方差多统计性和测度选取 与直方图描述子不同，协方差矩阵在计算测度时不位于欧式空间，不能直接使用常用的欧式空间距离进行计算。文献[20]中提出的测度方法是目前最常用的协方差测度

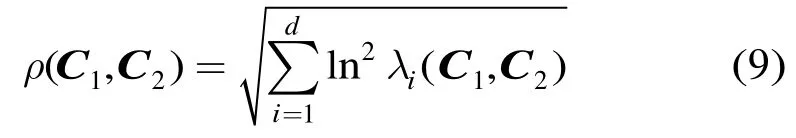
对于包含多个区域协方差矩阵的图像特征集，SCR方法首先基于上述测度累积两帧图像所有对应区域的协方差距离，然后从中剔除前20%的最大距离，形成两帧图像的最终距离。这样的测度方式对于较多的区域协方差而言计算量极大，从实验效果来看识别性能也不够理想(参见本文4.1.1节)。

文献[22]提出对协方差矩阵进行 Cholesky分解，以将协方差转换为欧式空间下的 Sigma集。Sigma集能够近似地保持协方差的统计特性，本文受其启发提出从协方差矩阵抽取多种统计向量来进行区域描述。选取的统计向量包括特征均值向量、特征标准差向量、特征相关系数向量和Sigma向量。

这4类统计向量的构造如下：特征均值向量即式(7)中的d维向量μ；提取协方差矩阵主对角线上的方差值进行开方运算，得到d维标准差向量；将协方差转换成相关系数矩阵，然后取其下三角部分(不含主对角线)进行向量化，形成维相关系数向量；将d阶协方差矩阵C进行Cholesky分解，获得对称阵L后向量化其下三角部分，形成维的 Sigma向量[22]。根据式(8)的映射函数可知 12d= ，将4类统计向量分别在图2所有的15个区域上进行级联，分别形成180, 180, 990和 1170维度的级联统计特征向量，分别记为。

获取4类统计特征向量后，MSPC方法的测度同样设计为4类特征向量1l距离的加权组合

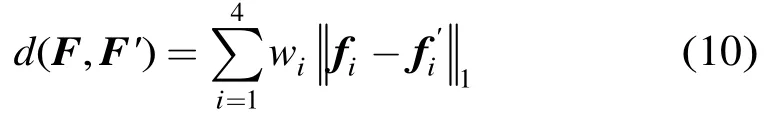
2.3 融合特征描述(HSCD)

上面提出的两种统计方法都使用了颜色和结构信息，但它们截然不同的特征统计方式使它们具有融合增强的潜质。MCSH特征是在多种颜色通道上级联多区域的空间和直方图信息，就颜色通道而言属于纵向级联；MSPC特征则是在多个区域上级联多种颜色和梯度通道的综合信息，就颜色通道而言属于横向融合。

因此，本文HSCD方法将上述两种统计方法进行融合，采用加权组合的方式

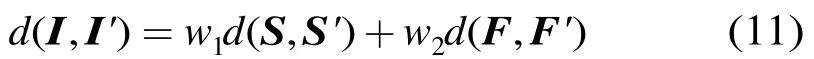
3 再识别性能评估

目前文献通常采用累积匹配特性曲线(Cumulative Matching Characteristic, CMC)[1]来评估人体再识别性能。CMC曲线反映的是在目标图库前n个最相似候选目标内找到探测图片正确匹配的概率。不同方法的 CMC曲线间可能存在交叉，目前没有统一的方式来综合评估 CMC曲线的性能。通常 CMC曲线下的归一化面积(normalized Area Under CMC, nAUC)能反映出CMC曲线的整体性能。文献[18]最近提出一种基于信息熵的指标PUR，该指标实际上反映的仍然是CMC曲线的整体性能。但目前多数文献只画出了 CMC曲线的前面部分，在没有代码和 CMC数据的情况下也难和其它方法进行基于整体指标的性能比较。

事实上，仅仅比较曲线的整体性能可能并不利于实际应用。例如，目标重捕通常选取目标库少量的最相似候选目标，尤其是相似度最高的候选目标。因此，从应用的角度出发，本文认为 CMC曲线真正有意义的部分是曲线前面部分。故本文提出使用CMC曲线的Rank-1, Rank-10%和nAUC-10% 3类指标合成实用性综合指标，记为 ACI(Application based CMC Index)。其中，Rank-1指标反映最相似候选目标刚好为探测图片目标的概率；Rank-10%指标反映在图库目标总数10%的候选目标内找到探测图片正确匹配的概率；nAUC-10%指标代表CMC曲线在Rank-1和Rank-10%范围间的归一化面积。对所有参与比较的CMC曲线，3类指标分别1l归一后再加权相加，合成反映相对实用性能的ACI综合指标，3类指标的权重分别设为0.25, 0.25, 0.5。采用ACI指标能够有效地比较目前多数文献的CMC曲线，而且能够更合理有效地反映出实际应用的识别性能。

4 实验结果及分析

本文在两个常用图库上进行了广泛的实验比较。本文方法在Intel Xeon 2 GHz服务器平台上使用Matlab实现，实验首先在VIPeR图库上进行单帧模式下的性能分析和比较，然后在i-LIDS图库上进一步验证多帧模式下的性能。

4.1 VIPeR图库实验

VIPeR图库是再识别文献中使用最多的单帧模式标准图库，它包含632对不同视角、姿态和光照条件下的行人。本文采用文献[1]提出的5轮2折交叉验证方法计算平均的 CMC曲线。实验采用与文献[6]相同的测试集划分，每轮实验从图库选出 316对行人，其中一半用作目标图库，另一半用作探测集。

4.1.1 HSCD方法分析

本文HSCD方法由MCSH和MSPC两种方法融合而成，实验首先考察这两种方法的性能和方法内部特征的性能。为了验证方法在计算时间上的优势，MCSH和MSPC方法分别考察了式(3)测度[19]和SCR方法测度[9]的识别性能和计算时间。实验还将HSCD方法和两种公开源码的方法(SDALF特征方法[3]和PRDC测度方法[17])进行了性能和时间上的综合比较。实验结果如图3所示，3个子图分别画出了MCSH, MSPC和HSCD方法的相关曲线，子图右下角标注处列出了方法的内部特征和部分方法的时间指标(即图库所有图片的特征提取时间1T，特征距离计算时间2T以及距离测度训练时间3T)。

图3(a)表明在MCSH方法的3类特征中，直方图信息优于空间信息，y方向的二阶空间信息优于一阶信息。式(3)空间直方图的传统测度方法计算时间极长，性能却略差于直方图方法。图 3(b)表明MSPC方法中的均值、相关系数和Sigma向量性能相当，均优于二阶方差信息。MSPC方法的4类特征存在极强的互补性，组合后其性能得到了很大提升，但其协方差传统测度方法同样存在计算时间长和性能较差的问题。

图3(c)表明MCSH和MSPC两种统计方法具有较强的互补性，融合后的HSCD方法优于SDALF特征方法和PRDC测度方法。在时间方面，本文方法不需要训练，且特征提取和测度计算的时间耗费非常小。SDALF方法依赖分割检测等预处理，特征提取时间最长；PRDC方法则训练时间长、训练时耗费内存量大(10 G左右内存)。

4.1.2当前方法比较 实验进一步和目前已有的特征和测度类方法进行比较。实验结果如图4所示，其中比较方法的 CMC曲线均从相应文献或代码中获得，图中竖直虚线代表目标库 Rank-10%(即 32)的位置。

表1列出了图4中CMC曲线的各项性能指标，包括排序为 1, 10%和 50时的识别率以及 nAUC-10%和ACI综合指标。

根据图4曲线和表1性能指标可得到如下结论。(1)在特征类方法中，HSCD方法各项性能指标均优于其它方法，包括目前最新的 SCEAF多特征组合方法和增强型eSDC方法；(2)即使与测度类方法相比，HSCD仍然优于多数方法，CMC曲线综合性能只略差于最新的LF测度方法。但本文HSCD方法的Rank-1指标达到29.3%，高出LF约21%，导致其ACI指标略高于LF; (3)与特征类方法相比，测度类方法主要增强了 CMC曲线的后面部分，测度方法在训练时存在的过度拟合等现象可能是导致曲线Rank-1取值较低的原因。

4.2 i-LIDS图库实验

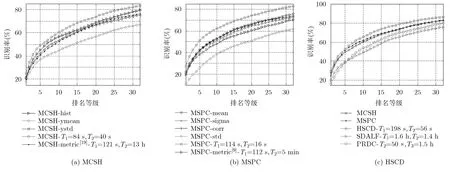
图3 VIPeR图库上HSCD方法的分析比较

图4 VIPeR图库上各方法的CMC曲线

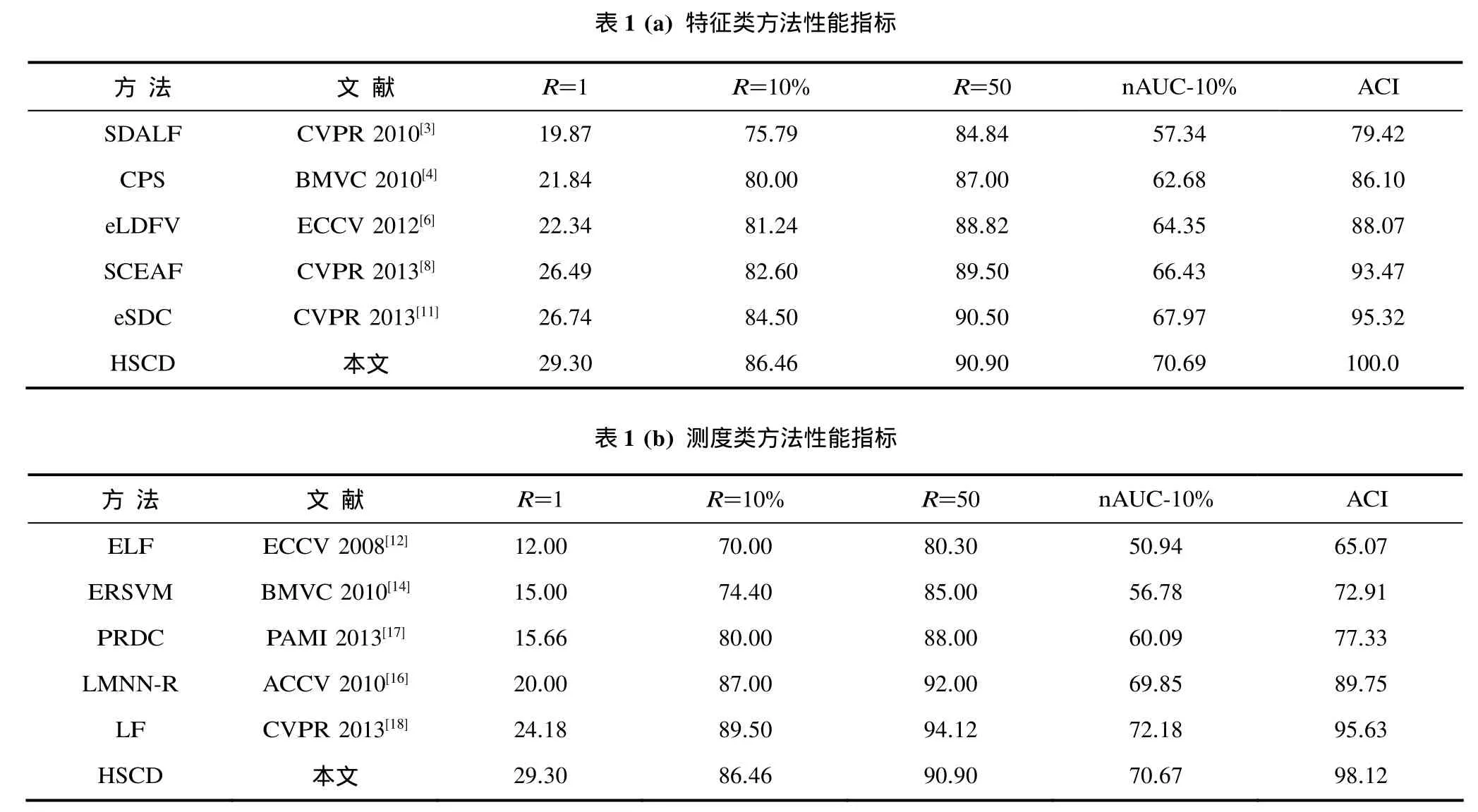
表1 VIPeR图库上各方法的识别率比较(%)

i-LIDS图库是常用的多帧模式人体再识别图库，该图库包含某机场119个行人的476张图片(每个行人平均4张图片)。该图库不仅存在行人视角、姿态和光照方面的变化，还存在较严重的部分遮挡现象。

本文在该图库上进一步验证HSCD方法在单帧和多帧模式下的性能。单帧模式下每个行人随机选取一张图片构成目标库，所有剩余图片构成探测集。多帧模式下每个行人随机选取两张图片构成目标库，再从剩余图片随机选取两张构成探测集(对于只有2张或3张图片的行人，分别随机选取1张和2张放入目标库，其余放入探测集)。单帧和多帧模式均进行100次实验，实验结果如图5所示。

从图5的CMC曲线可看出，HSCD方法在单帧和多帧模式下均优于其它方法。单帧模式下HSCD的Rank-1为36%，多帧模式下上升到58%，表明了HSCD方法在多帧模式下显著的增强作用。在多帧模式下，只有基于协方差测度学习的COSMATI方法能在 CMC曲线的后半段略优于HSCD，其它方法均明显差于HSCD。

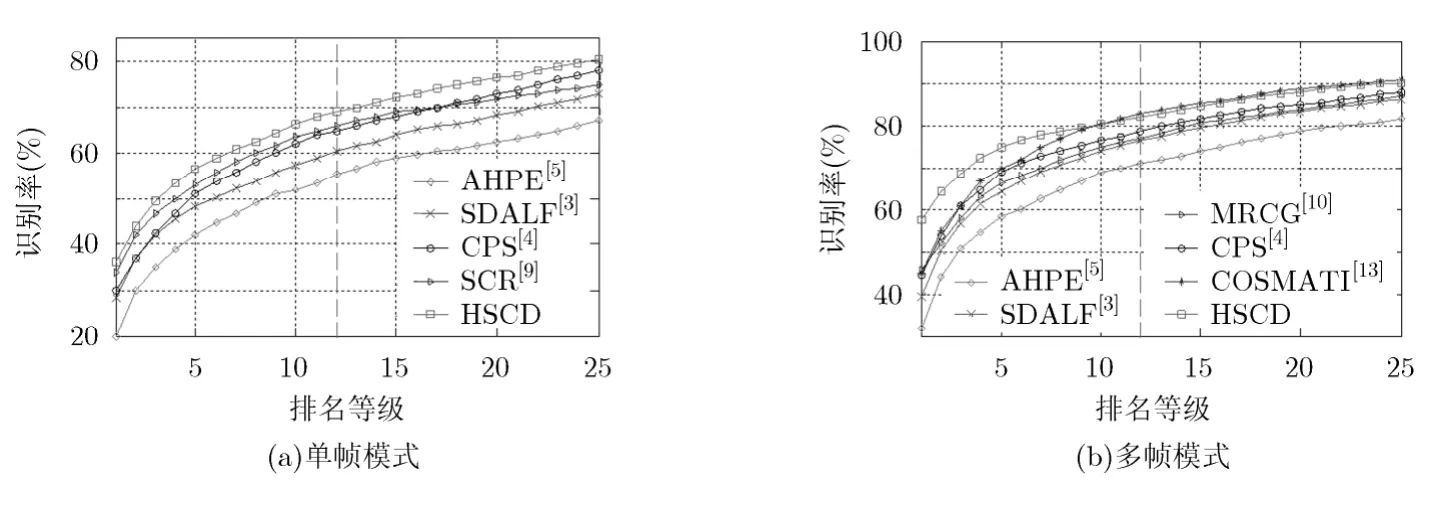
图5 i-LIDS图库上各方法的CMC曲线

以上实验结果表明，本文提出的HSCD方法在单帧和多帧模式下均可取得很好的识别性能。与其它方法相比，本文方法的ACI应用型指标更高，计算时间更少，更利于在实际应用中进行实时的人体再识别。

5 结束语

本文成功构造了基于空间直方图和协方差的两种外观统计描述方法，然后融合得到了性能优异的HSCD方法。该方法除了识别性能上的优势，其它优势还包括：(1)属于特征类方法，不需要进行监督性训练；(2)特征性能优异，MCSH和MSPC方法均不需要进行分割检测等预处理步骤，特征提取迅速；(3)测度简单，本文将传统测度替换为简单的1l距离加权组合测度，更利于高效的距离计算；(4)实用，本文方法ACI应用性能指标优异，有利于实时的视觉应用。

鉴于人体再识别存在的挑战性和对其它应用的重要性，下一步可能的研究工作还包括：(1)考察与颜色和结构信息具有较强互补性的其它特征，并寻找其它优秀的特征描述方法；(2)探讨针对各影响因素下的处理策略，如颜色和光照处理等；(3)基于本文特征考察和设计合适的测度学习方法；(4)将再识别方法引入到多机跟踪等应用领域，将人体再识别推广到其它目标的再识别问题，考察方法的实用性能和推广能力。

[1] Gray D, Brennan S, and Tao H. Evaluating appearance models for recognition, reacquisition, and tracking[C]. IEEE International Workshop on Performance Evaluation for Tracking and Surveillance. Rio de Janeiro, Brazil, 2007:41-47.

[2] Wang H, Bao X, Choudhury R R, et al.. Insight: recognizing humans without face recognition[C]. Proceedings of the 14th Workshop on Mobile Computing Systems and Applications,Georgia, USA, 2013, 7.

[3] Farenzena M, Bazzani L, Perina A, et al.. Person re-identification by symmetry-driven accumulation of local features[C]. IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, USA, 2010: 2360-2367.

[4] Cheng D S, Cristani M, Stoppa M, et al.. Custom pictorial structures for re-identification[C]. British Machine Vision Conference, Dundee, UK, 2011, 6.

[5] Bazzani L, Cristani M, Perina A, et al.. Multiple-shot person re-identification by chromatic and epitomic analyses[J].Pattern Recognition Letters, 2012, 33(7): 898-903.

[6] Ma B, Su Y, and Jurie F. Local descriptors encoded by fisher vectors for person re-identification[C]. European Conference on Computer Vision, Florence, Italy, 2012: 413-422.

[7] 范彩霞, 朱虹, 蔺广逢, 等. 多特征融合的人体目标再识别[J].中国图象图形学报, 2013, 18(6): 711-717.Fan Cai-xia, Zhu Hong, Lin Guang-feng, et al.. Person re-identification based on multi-features[J]. Journal of Image and Graphics, 2013, 18(6): 711-717.

[8] Hu Y, Liao S, Lei Z, et al.. Exploring structural information and fusing multiple features for person re-identification[C].IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Portland, USA, 2013: 794-799.

[9] Bak S, Corvee E, Brémond F, et al.. Person re-identification using spatial covariance regions of human body parts[C].IEEE International Conference on Advanced Video and Signal Based Surveillance, Boston, USA, 2010: 435-440.

[10] Bak S, Corvee E, Bremond F, et al.. Multiple-shot human re-identification by mean riemannian covariance grid[C].IEEE International Conference on Advanced Video and Signal-Based Surveillance, Klagenfurt, Austria, 2011:179-184.

[11] Zhao R, Ouyang W, and Wang X. Unsupervised salience learning for person re-identification[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Portland, USA, 2013: 4321-4328.

[12] Gray D and Tao H. Viewpoint invariant pedestrian recognition with an ensemble of localized features[C].European Conference on Computer Vision, Marseille, France,2008: 262-275.

[13] Back S, Charpiat G, Corvée E, et al.. Learning to match appearances by correlations in a covariance metric space[C].European Conference on Computer Vision, Florence, USA,2012: 806-820.

[14] Prosser B, Zheng W S, Gong S, et al.. Person re-identification by support vector ranking[C]. British Machine Vision Conference, Wales, UK, 2010, DOI: 10.5244/c.24.21.

[15] 陈方, 许允喜. 视频监控中基于在线多核学习的目标再现识别[J]. 光电工程, 2012, 39(9): 65-71.Chen Fang and Xu Yun-xi. People re-identification based on online multiple kernel learning in video surveillance[J].Opto-Electronic Engineering, 2012, 39(9): 65-71.

[16] Dikmen M, Akbas E, Huang T S, et al.. Pedestrian recognition with a learned metric[C]. Asian Conference on Computer Vision, Queenstown, New Zealand, 2010: 501-512.

[17] Zheng W S, Gong S, and Xiang T. Reidentification by relative distance comparison[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(3):653-668.

[18] Pedagadi S, Orwell J, Velastin S, et al.. Local fisher discriminant analysis for pedestrian re-identification[C].IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Portland, USA, 2013: 3318-3325.

[19] Birchfield S T and Rangarajan S. Spatiograms versus histograms for region-based tracking[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, USA, 2005: 1158-1163.

[20] Tuzel O, Porikli F, and Meer P. Region covariance: a fast descriptor for detection and classification[C]. European Conference on Computer Vision, Graz, Austria, 2006:589-600.

[21] Zheng W, Gong S, and Xiang T. Associating groups of people[C]. British Machine Vision Conference, London, UK,2009: 1-11.

[22] Hong X, Chang H, and Shan S. Sigma set: a small second order statistical region descriptor[C]. IEEE Conference on Computer Vision and Pattern Recognition, Miami, USA,2009: 1802-1809.