基于线性阈值模型的影响力传播权重学习

郭 静曹亚男周 川张 鹏郭 莉

①(北京邮电大学计算机学院 北京 100876)②(中国科学院信息工程研究所 北京 100093)

1 引言

随着互联网技术的不断发展，社交网络成为人们交流互动的新场所[1]。在社交网络中，用户通过影响力的传播作用影响着网络中其他用户的情感、观点和行为。因此，用户间的影响力度量问题引起大量研究[212]-。早期的研究往往基于社交网络的拓扑信息，利用常数赋值法、度平均计算法[25]-、随机赋值法[2,6]来估算用户间的影响力。然而，这些方法缺少系统的学习与分析，且忽略了用户历史行为的作用。为此，一些研究工作以用户的历史行为为基础，利用统计和模型学习的方法来度量用户之间的影响力。例如：文献[7]在用户历史行为记录的基础上，利用期望最大化(Expectation-Maximization,EM)算法估算用户间的影响力。文献[8]以 Jaccard系数和伯努利分布为基础，提出若干概率模型来建模用户间的影响力学习问题。文献[9]从主题模型的角度研究传播影响力, 并计算出基于主题有效的独立级联模型(Topic-aware Independent Cascade,TIC)的相关参数。然而，此类方法在建模时，都假设用户的激活行为是相互独立的。在现实中，用户的朋友可能共同影响其做出某一行为，所以上述方法不能全面度量用户之间的影响力。

为解决上述问题，本文以线性阈值(Linear Threshold, LT)模型[4,13]为基础来学习用户之间的影响力。为此，我们将会面临下列挑战。首先，LT模型以权值来度量用户间影响力，缺少相应的概率描述，所以无法直接使用最大似然估计方法对问题建模。其次，由于用户间影响力度量与多个邻居用户的历史行为相关，所以每个用户都需要建立不同目标函数，如何对不同的目标函数有效求解是一个难点。

为此，本文基于 LT模型，利用最大熵原理估计激活阈值的概率密度函数；并以此计算邻居激活给定用户的概率，并将用户的历史行为日志看作样本，借鉴最大似然估计的思想对用户间影响力学习问题建模；最后，设计一种改进的粒子群算法来求解问题。该算法根据问题目标函数和约束的特点，通过问题映射、适应度函数建立、越界阻止、动态参数设置和最优粒子变异等优化策略，有效地学习用户间影响力。

2 相关预备知识

LT模型是一种能够刻画“影响力累计特性”的传播模型。考虑到现实中用户可能被其若干朋友共同影响，本文基于LT模型来学习用户间的影响力。本节先回顾相关预备知识，表1是相关数学符号表示。

表1 对应数学符号表示

在 LT模型中，每个节点存在激活或未激活状态，且只处于两者之一。每条边都被赋予，以表示w对u的影响力，反映u被邻居激活的可能性。当激活邻居的所有权重和超过该点阈，如式(1)，则该节点被激活；否则激活失败。

另外，对每个节点u，所有邻居对其产生的影响力权重之和不能超过1。

3 基于LT模型的影响力传播权重学习方法

3.1 基于最大熵的激活概率计算

LT模型以权值来度量用户之间的影响力，缺少相应的概率描述，无法直接借鉴最大似然估计的思想来对问题进行建模。为此，本文首先根据 LT模型的特点来估计邻居激活用户的概率。

在 LT模型中，邻居是否能激活给定用户，是由邻居对给定用户的影响力和激活阈值所共同确定的。因此在影响力确定的条件下，邻居激活用户的概率是由激活阈值uθ所决定的。用户是否发生行为受多种因素影响，所以激活阈值具有很强的不确定性。为刻画这种不确定性，本文以最大熵原理来估计激活阈值的概率密度，并以此为基础来计算邻居激活用户的概率。

定理1 已知激活阈值uθ的取值范围在[0,1]之间，且的概率密度函数满足等式(4)，则激活阈值的最大熵分布的概率密度函数满足。

证明 根据最大熵原理[14]，在满足约束的条件下，熵值最大的分布就是符合实际的分布。由于没有先验知识，仅知道uθ的取值范围在[0,1]之间，所以求解的概率密度，就是求解下列约束优化问题。其中，是激活阈值的熵值，C为常数。

为此，首先用拉格朗日乘子法将约束加入目标形成新目标函数式(5)，然后使用求导方法计算问题的最优值。

证毕

在定理1的基础上，本文利用激活阈值uθ的概率密度函数来计算邻居激活用户的概率。假设邻居对用户u的影响力为，则邻居成功激活用户的概率可由式(8)计算获得，邻居激活用户失败的概率可由式(9)计算获得。

3.2 问题建模

根据用户的历史行为日志，本文借鉴最大似然估计的思想，对用户影响力学习问题建模。即：将日志信息看作是基于 LT模型产生的样本，利用用户影响力取值使样本观测的概率最大的思想对问题建模。本文使用三元组{用户-事件-时间}来表现日志中用户在事件上的激活状态，U表示用户集合，D表示事件集合，T表示时间集合。针对历史日志中的某事件，用户u的状态分两种情况讨论：

(1)u激活：若其所有邻居的激活时间都晚于u，则表示u自发参与到iD的传播中；若存在邻居的激活时间都早于u，则表示u受到邻居影响才参与到的传播中，它是邻居成功激活用户的样本。

(2)u未激活：若其所有邻居都处于未激活状态，则表示u既没有受到来自邻居的影响，也没有自发地参与；若存在激活的邻居，则表示邻居对u的激活失败，它是邻居激活用户失败的样本。

根据日志里的用户信息，本文利用式(10)描述用户间影响力学习的目标函数。即

3.3 求解算法

本文根据问题目标和约束条件，设计一种改进粒子群算法(Improved Particle Swarm Optimization Algorithm for Influence Weights Learning, IWL-IPSO)来求解问题。其优化策略包括：(1)问题映射，(2)适应度函数建立，(3)越界阻止，(4)动态参数设置，(5)最优粒子变异等。

3.3.1粒子群算法回顾 粒子群算法[15]是一种基于群体智能的启发式全局搜索算法。它从随机解出发，迭代搜索问题的最优解。即根据粒子的最好位置和粒子群中最优粒子的位置，使用式(14)和式(15)来更新位置信息。

3.3.2问题的粒子映射 问题的合理映射是粒子群算法求解问题的前提，由于线性阈值模型中用户的状态受邻居的影响，所以本文将邻居用户对用户u的影响力的组合表示成一个粒子，具体如图1所示。

图1 问题的粒子映射

3.3.3适应度函数设计 适应度函数是粒子群算法学习用户间影响力的关键。由于的计算结果与历史事件的数量| |D 相关，且满足约束条件和，故当较大时，有，难以评价方案适应度；此外，不满足约束方案中也可能包含着最优解的影响力取值。为此，本文设计一种新的适应度函数，即采用开| |D 次方的形式来增大适应度的取值，并使用分段处理策略来综合评价影响力权重，如式(16)。

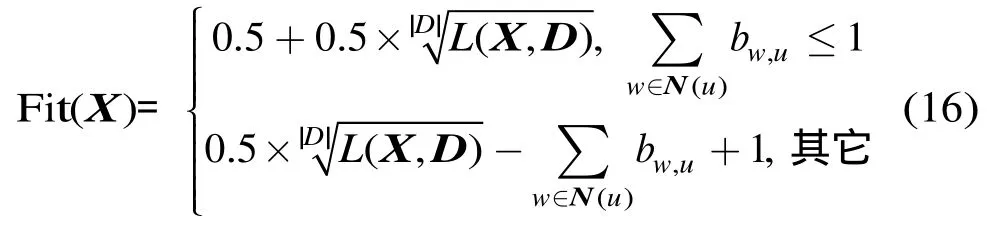
3.3.4约束违背控制 由于LT模型中的用户影响力取值范围在[0,1]，传统粒子群算法没有直接方法来限制粒子位置，使得粒子在搜索过程容易飞离搜索区域，产生无效的影响力权重。为了使更多粒子在有效的区域中搜索，本文在位置更新式(15)中加入动力参数设置，具体如式(17)所示。

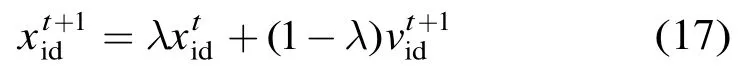
3.3.5动态参数设置 在用户影响力学习的过程中，算法的全局和局部搜索能力共同决定了学习的效果。文献[16]指出，当惯性权重取值w较小时，算法将拥有较强的局部搜索能力，有利于粒子收敛。当惯性权重取值w较大，将增强粒子的探索能力，使得算法的全局搜索能力得到提高。为平衡二者的关系，本文以递减函数来改变w的取值，让w的取值随着迭代过程逐渐递减，其函数表达如式(18)所示。

4 实验

为验证本方法的合理性，在多次实验的结果上，以方法执行时间、用户间影响力的适应度为评价指标来综合分析IWL-IPSO算法的性能。其中，数据集合来自文献[17]，对比算法的描述情况：

(1)IWL-PSO(Particle Swarm Optimization algorithm for Influence Weights Learning)：该算法直接利用传统粒子群算法来学习用户间的影响力。

(2)IWL-Degree(Degree algorithm for Influence Weights Learning)：该算法直接根据社交网络中邻居的数目计算用户间的影响力。

(3)IWL-PSOA(Particle Swarm Optimization algorithm A for Influence Weights Learning)：该算法在IWL-IPSO的基础上，通过去除约束违背控制操作来学习用户间的影响力。

(4)IWL-PSOB(Particle Swarm Optimization algorithm B for Influence Weights Learning)：该算法在IWL-IPSO的基础上，通过去除动态参数设置操作来学习用户间的影响力。

(5)IWL-PSOC(Particle Swarm Optimization algorithm C for Influence Weights Learning)：该算法在IWL-IPSO的基础上，通过去除最优粒子变异策略来学习用户间的影响力。

4.1 方法有效性验证

为验证方法的有效性，本次实验将从数据集中选择拥有不同历史行为记录的用户为分析对象，利用IWL-IPSO, IWL-PSO和IWL-Degree来学习邻居用户对他们的影响力，并根据算法的执行时间和用户间影响力的适应度来分析方法在不同历史行为记录下的性能。其中，被选目标用户的详细信息如表2所示。

图2和图3是IWL-IPSO, IWL-PSO和IWLDegree在20次实验中对用户间影响力学习所使用的平均时间及获得的平均适应度。从图2中可以看出，在邻居数目相同的情况下，IWL-IPSO的执行时间随历史信息数量的增长呈线性增长。从图3可以看出，IWL-IPSO在不同历史行为记录下均取得较好的适应度。

表2 被选用户的情况

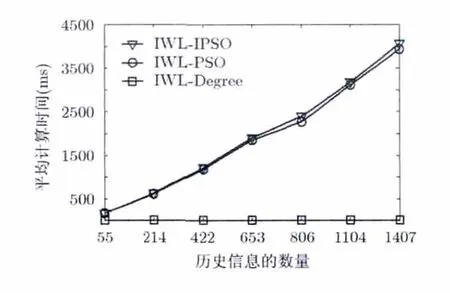
图2 不同算法执行的平均时间

4.2 方法的性能分析

为进一步分析方法的性能，实验选择具有不同邻居数目、不同历史行为记录的用户为分析对象，通过去除IWL-IPSO的优化步骤来分析它们对学习效果的影响。被选择的用户信息如表3所示，实验结果如表4和表5所示。

从表3和表4可以看出，每个改进步骤都可以提高影响力学习的适应度，且步骤的花费时间较方法整体时间而言相对较少。其中，IWL-PSOA在使用约束违背控制策略后，其学习影响力的适应度较原方法提高了0.34%，这是因为该策略对传统的更新值进行了缩放，尽可能让用户间的影响力满足约束。IWL-PSOB在使用动态参数设置策略后，其学习影响力的适应度较原方法提高了0.25%，这是因为该策略平衡了算法的局部和全局搜索的能力，粒子在算法的执行初期，更加注重信息的获取；而在算法的执行后期，更加倾向于对当前最优方案方向进行搜索，从而提高算法的收敛性。IWL-PSOC在使用最优粒子变异策略后，其学习影响力的适应度较原方法提高了4.43%。这是因为在传统的粒子群算法中，最优粒子的运动具有盲目性，可导致算法收敛于局部最优解，出现早熟现象，而最优粒子变异策略可以有效克服上述问题。

表3 性能分析所选择用户的情况

表4 不同算法学习用户间影响力获得的平均适应度

图3 不同算法学习用户间影响力获得的平均适应度

表5 不同方法在影响力学习的计算时间(ms)

5 结束语

本文在线性阈值模型的框架下，提出一种影响力传播权重的计算方法。该方法基于社交网络中用户的历史行为日志信息，利用优化的粒子群算法来学习用户间的影响力。同时，本文基于真实的社交网络数据和相关用户的历史行为日志，实验证明了本文方法的有效性。

[1] Park B, Lee K, and Kang N. The impact of influential leaders in the formation and development of social networks[C].Proceedings of the 6th International Conference on Communities and Technologies(C＆amp;T), New York, USA,2013: 8-15.

[2] Chen Wei, Wang Chi, and Wang Ya-jun. Scalable influence maximization for prevalent viral marketing in large-scale social networks [C]. Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining(KDD), Washington, USA, 2010: 1029-1038.

[3] Chen Wei, Wang Ya-jun, and Yang Si-yu. Efficient influence maximization in social networks[C]. Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), Paris, France, 2009: 199-208.

[4] Kempe David, Kleinberg Jon, and Tardos Eva. Maximizing the spread of influence through a social network[C].Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), Washington, USA, 2003:137-146.

[5] Zhou Chuan, Zhang Peng, Guo Jing, et al.. UBLF: an upper bound based approach to discover influential nodes in social networks[C]. Proceedings of the IEEE International Conference on Data Mining (ICDM), Dallas, USA, 2013:907-916.

[6] Jung Kyomin, Heo Wooram, and Chen Wei. IRIE: scalable and robust influence maximization in social networks[C].Proceedings of the IEEE International Conference on Data Mining (ICDM), Brussels, Belgium, 2012: 918-923.

[7] Saito Kazumi, Nakano Ryohei, and Kimura Masahiro.Prediction of information diffusion probabilities for independent cascade model[C]. Proceedings of the International Conference on Knowledge-Based and Intelligent Information ＆amp; Engineering Systems (KES), Zagreb, Croatia,2008: 67-75.

[8] Goyal Amit, Bonchi Francesco, and Lakshmanan Laks V S.Learning influence probabilities in social networks[C].Proceedings of the ACM International Conference on Web Search and Data Mining (WSDM), New York, USA, 2010:241-250.

[9] Barbieri Nicola, Bonchi Francesco, and Manco Giuseppe.Topic-aware social influence propagation models[C].Proceedings of the IEEE International Conference on Data Mining (ICDM), Brussels, Belgium, 2012: 81-90.

[10] Liu Lu, Tang Jie, Han Jia-wei, et al.. Learning influence from heterogeneous social networks[J]. Data Mining and Knowledge Discovery, 2012, 25(3): 511-544.

[11] Konstantin Kutzkov, Albert Bifet, Francesco Bonchi, et al..STRIP: stream learning of influence probabilities[C].Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), Chicago, USA, 2013:275-283.

[12] Goyal Amit, Bonchi Francesco, and Lakshmanan Laks V S.A data-based approach to social influence maximization[C].Proceedings of the International Conference on Very Large Data Bases (VLDB), Istanbul, Turkey, 2012: 73-84.

[13] Goyal Amit, Lu Wei, and Lakshmanan Laks V S. Simpath:an efficient algorithm for influence maximization under the linear threshold model[C]. Proceedings of the IEEE International Conference on Data Mining (ICDM),Vancouver, Canada, 2011: 211-220.

[14] Jaynes E T. Information theory and statistical mechanics[J].Physical Review, 1957, 106(4): 620-630.

[15] Eberhart Russell and James Kennedy. A new optimizer using particle swarm theory[C]. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 1995: 39-43.

[16] Shi Yuhui and Eberhart Russell. A modified particle swarm optimizer[C]. Proceedings of IEEE World Congress on Computational Intelligence, Anchorage, USA, 1998: 69-73.

[17] Liu Lu, Tang Jie, Han Jia-wei, et al.. Mining topic-level influence in heterogeneous networks[C]. Proceedings of the Conference on Information and Knowledge Management(CIKM), Toronto, Canada, 2010: 199-208.