粘贴压电层功能梯度材料Euler梁热屈曲前自由振动的半解析数值法
苏厚德, 樊建领, 俞树荣, 冯玉洁, 曹维国
(1. 甘肃蓝科石化高新装备股份有限公司,兰州730070;2.兰州理工大学 石油化工学院,兰州730050)
用压电材料制成的作动器在结构智能控制中已经具有广泛的应用。关于压电智能结构控制的研究工作主要涉及梁、板、壳结构的静动态响应控制[1~17]。Crawley 和Luis[1]对于压电层合梁做出有意义工作,给出了压电材料与结构体之间的静动态藕合模型,并通过实验验证了理论结果的可靠性,但是在Crawley 的梁模型中没有考虑横向剪切变形以及轴向力的影响,Zhou 等[2],Xia 等[3]对表面粘贴压电片的梁式板和变厚度板结构的几何非线性大变形及振动响应智能控制进行了研究。丁丽霞等[4]考虑上下嵌有功能梯度原件的薄板,基于经典板理论,导出了基于功能梯度弹性薄板小挠度屈曲平衡微分方程,研究了材料的梯度指数对于临界电压的影响。Dai 等[5]基于一阶剪切理论同时考虑热-电-机耦合效应,用无网格Galerkin 法对含有压电驱动和传感的FGM 板静动态响应做了研究。林启荣等[6]分析了压电驱动器对弹性梁的等效作用,并给出了一端固支一端简支梁的解析解。Fridman 等[7]基于一阶剪切理论,研究了对称和非对称铺设压电层的柔性层合复合梁的固有频率,屈曲载荷等与轴向、厚度方向载荷及电场载荷之间的特征曲线关系。Shen等[8,9]、Huang 等[10]基于Reddy 高阶剪切理论和von Karman 几何非线性方程,同时考虑物性参数的温度依赖效应,采用摄动法对压电-功能梯度板结构的屈曲、过屈曲、振动做了研究,给出热、电载荷对压电-功能梯度板的屈曲、振动的影响。不少科研人员还研究了热、机、电多种载荷耦合作用下压电层合智能结构的静动态响应[11~13]。其中,Yang 等[13]基于高阶剪切理论,用以微分求积和Galerkin 法为基础的半解析方法,研究了各种边界条件下,功能梯度层合板的非线性振动问题。作者同时考虑了温度,压电层施加电压驱动,但是没有考虑非均匀升温,指出在大变形下固有频率是非常“敏感的”。于涛等[14]采用Airy 应力函数法推导出了压电功能梯度材料悬臂梁二维平面问题解析解。丁皓江等[15,16]系统地研究了横观各向同性压电板、壳的三维问题,给出了相应的解析通解。LI[17]等将功能梯度Timoshenko梁问题归结为含有中面位移、横截面转角、横截面内力以及变形后的轴线弧长共7个基本未知函数的非线性常微分方程边值问题,采用打靶法数值求解所得强非线性边值问题,研究了升温时的屈曲和过屈曲响应解,给出了梁的过屈曲平衡路径,详细分析了热载荷和材料梯度性质对变形及过屈曲的影响。
但作者未见关于压电层合梁和压电功能梯度材料梁的分析中,对热-电载荷共同作用下FGM-Euler梁屈曲前的自由振动问题,给出半解析数值解的报道。本工作拟在文献[18,19]的基础上,对上下表面粘贴压电层的FGM 层合梁在横向非均匀升温以及对压电层施加驱动电压载荷下的几何非线性大变形进行定量分析。基于轴向可伸长梁的精确几何非线性理论,建立压电-功能梯度Euler 梁在热-电-机械载荷作用下的几何非线性动力学控制方程,将问题归结为含有中面位移、横截面转角、横截面内力以及变形后的轴线弧长等14个基本未知函数的非线性常微分方程边值问题。把问题线性化以后,得到两端固定和简支的压电-FGM 层合梁在横向均匀电场和非均匀升温作用下线性振动的半解析数值解。
1 问题的数学模型
考虑压电材料和功能梯度材料组成的层合梁。其上、下表面层为压电材料,厚度均为t,中间层为功能梯度材料,厚度为h。梁的长度l,宽度为b,总厚度为h0。为研究方便,只考虑逆压电效应,并且认为压电层与功能梯度层之间牢固粘贴。这里,研究梁在温度载荷和电压作用下的静动态响应,分析通过对压电层的电压驱动实现对梁的热静态变形,振动固有频率的调整作用。在问题的数学模型建立中考虑梁的轴向伸长。
1.1 非线性几何方程
精确考虑梁的轴线伸长,可得梁变形后轴线的几何方程[17,18]:
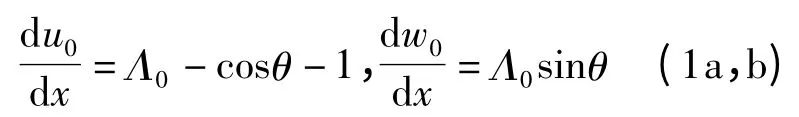
其中,x 为变形前梁轴线上任意一点的物质坐标,且x ∈[0,l];u0(x)和w0(x)分别为轴线上的点在x,z 方向的位移,θ(x)为梁变形后轴线切线与x 轴正向的夹角,Λ0为轴线伸长率。假设梁变形过程中横截面仍然保持为平面,可以求得横截面上任意点处的正应变为[17~19]:
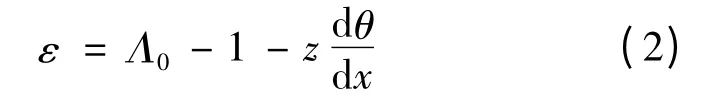
其中θ 为横截面法线与x 轴之间的夹角。
1.2 本构方程
假设材料为线性热弹性材料,并且梁的各层之间截面上的变形是连续的,由此可得压电-FGM 层合梁中第j 层的物理方程[9,10]:
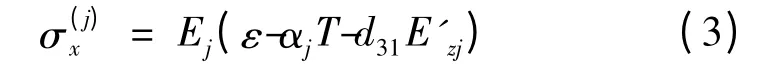
其中:Ej,Gj,αj和E'zj分别为第j 层的拉伸弹性模量、剪切弹性模量、热膨胀系数和电场强度(j = 1,2,3 ),d31为压电应变常量,T 为升温。考虑外电压只沿厚度方向作用,则压电层的电场强度可以表示为[9,10]:

Vj为第j 层的电压,t1= t3= t,t2=h。这里由于只有上下表层存在电压,所以:V2= 0 。
设功能梯度材料中间层由陶瓷和金属两种材料组成,并且由上表面的纯陶瓷连续变化为下表面的纯金属。FGM 的材料的物性参数(弹性模量E、泊松比ν、热膨胀系数α 和热传导系数K 等)满足下列关系[8,10]
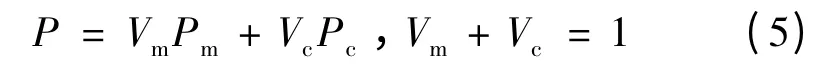
其中Vm,Vc分别为金属和陶瓷的体积分数。这里假设陶瓷体积分数沿厚度方向坐标按幂函数变化,即:
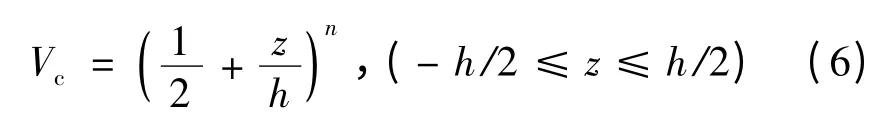
其中n 为陶瓷材料的体积分数指数(0 ≤n <∞)。考虑到功能梯度材料仍属于各向同性材料,所以弹性常数之间满足关系G = E/[2(1 + ν)]。
考虑到压电层为各向同性材料;极化方向只沿z 轴方向。将式(2)代入式(3)可得内力表达式:
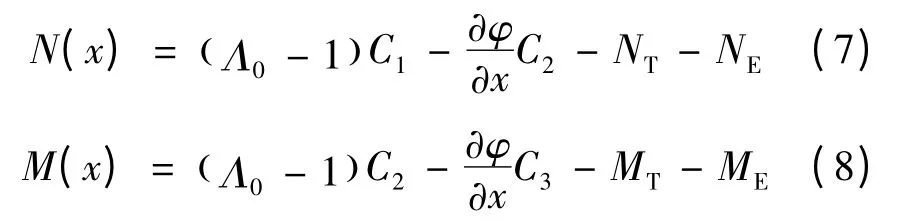
其中C1,C2和C3分别为刚度系数;NT,NE分别为热轴力和电轴力,MT,ME分别为热弯矩和电弯矩,具体定义为:

1.3 热传导方程
考虑层合梁受横向非均匀升温作用。设上表面升温为TU,下表面升温为TL。梁内的升温场可由下列一维热传导方程确定:
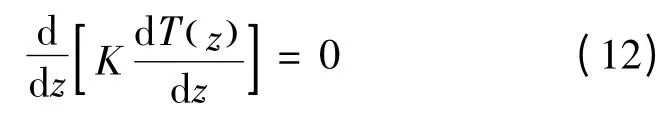
由于压电层为均匀材料,热传导系数为常数。因此,由式(16)可知上、下层的升温为线性函数。中间层功能梯度材料的热传导系数为横向坐标z 的已知函数,具体可由式(14)给出。由上、下表面的边界条件和界面出处的连续性条件可以确定各层的升温场分别如下[10]:
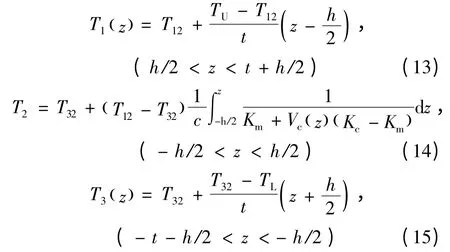
其中T12和T32分别为功能梯度层上表面和下表面(或上、下界面)处的温度。具体表达式为:
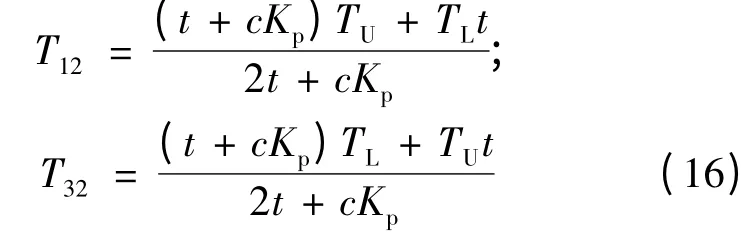
其中Ki( i=p,c,m )分别表示压电、陶瓷和金属材料的导热系数;c 为常数,其表达式为:
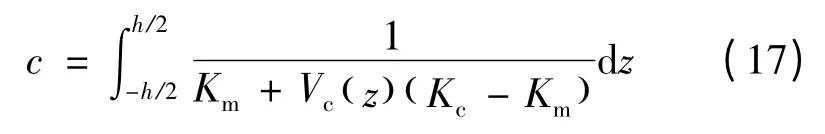
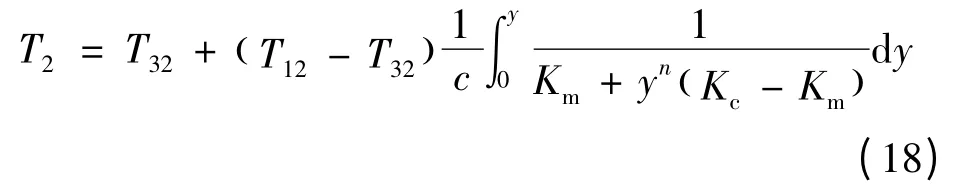
其中
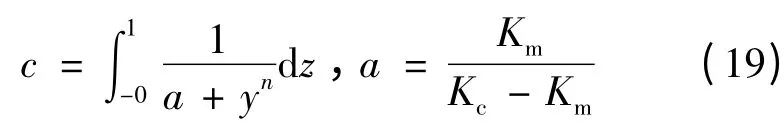
1.4 平衡方程
采用轴线可伸长几何非线性理论,可得Euler梁在变形后构形的平衡方程[18,19]:

其中:H,V 分别为横截面内的水平和横向内力分量;(qx,qz)为作用于梁上的分布力;qθ为分布力矩。由静力等效关系知,变形后横截面内法向内力N 可由H,V 表示为:
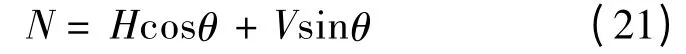
由方程(7,8)和(21)可以解得:
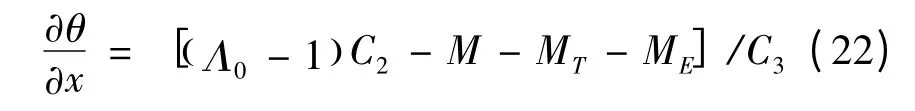
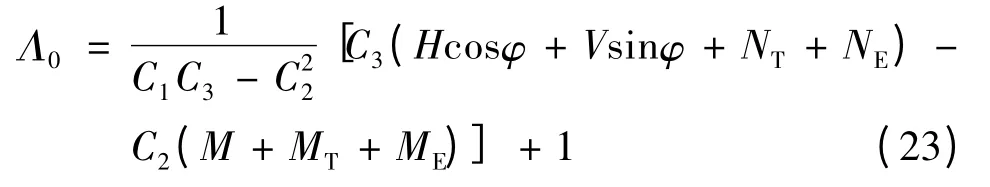
若只考虑自由振动,其惯性力可以表示为:

其中:I0,I1分别为轴线伸长后单位长度的质量分布和单位长度的转动惯性矩。表达式为:
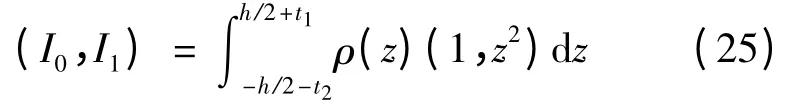
至此,式(1),(20),(22)就构成了压电-功能梯度Euler-Bernoulli 梁在热-电-机载荷同时作用下的几何非线性力学行为的控制方程。其中包含了轴线位移u0(x),w0(x),横截面转角θ(x)以及等效内力H(x),V(x)和弯矩M(x)等14个基本未知函数,它们都是物质坐标x 的函数。由式(22),(23)可知,轴线伸长率Λ0和横截面转角θ 也可以表示为上述基本未知函数的表达式。
2 无量纲控制方程
为便于计算和分析,将上述控制方程转化为无量纲形式。为此,引入下列无量纲量:
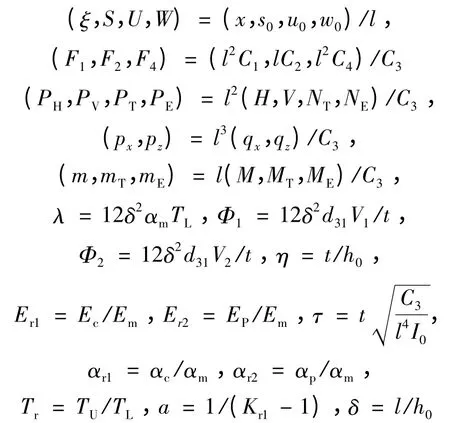
将上述无量纲变换代入式(1),(20),(22),得到压电-FGM 层合梁无量纲的动力学控制方程:
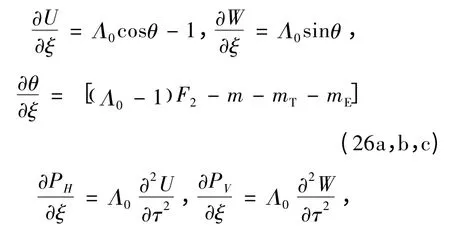

其中:
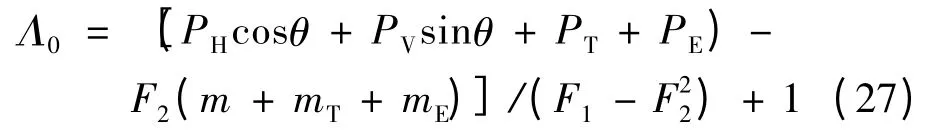
控制方程中的无量纲电轴力、电弯矩的表达式见式(28),(29)。上下表层电场同向(即V1= - V2= V[7])时:
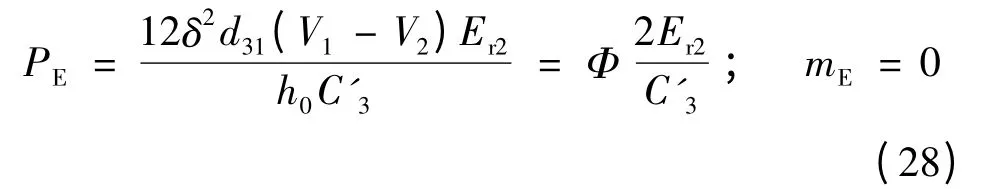
上下表层电场异向(即V1= V2= V[7])时:
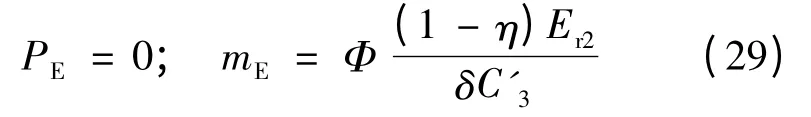
考虑梁的约束是两端为固定和简支,则相应的无量纲边界条件可表示为式(30)和(31):
1)fixed-fixed
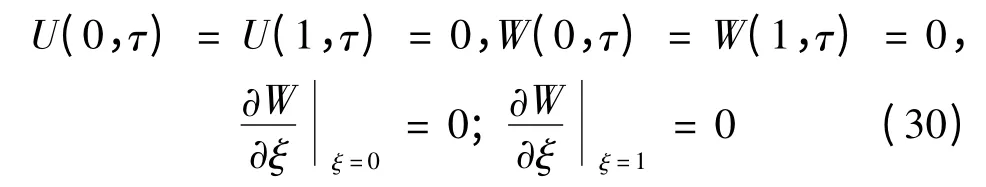
2)pinned-pinned
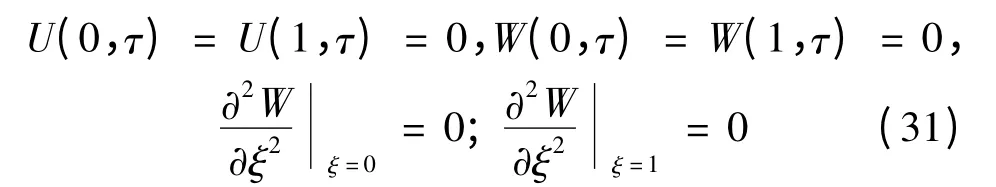
假设梁处于平衡状态,在控制方程式(26)中,假设令sinθ = θ,cosθ = 1,并略去所有非线性项,则可得线性化问题:
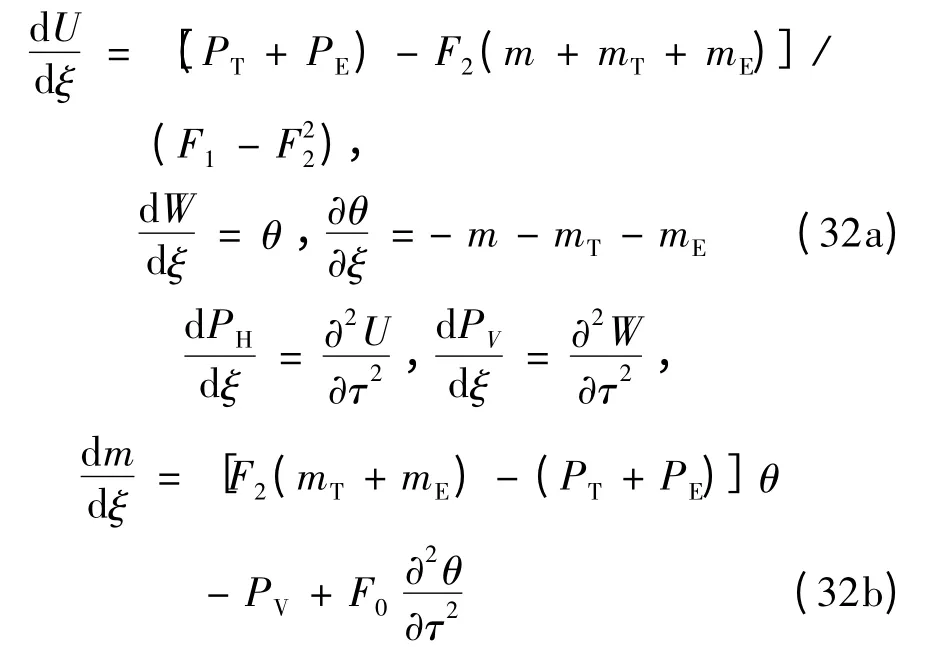
从上面的方程中消去PH,PV,m,θ,得到只含基本位移U,W 的方程:
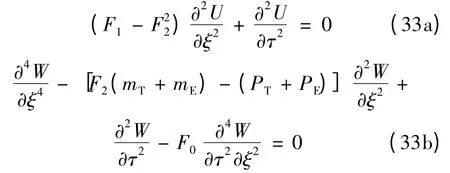
于是得到对称贴压电层的功能梯度梁在未屈曲状态的线性振动控制方程式(33)。可以看出横向振动和纵向振动是非耦合的,两式可以独立求解。设梁的自由振动响应为:

其中,ω1,ω2分别为纵向和横向振动的无量纲固有频率,φ1,φ2为常数。将式(34a,b)带入控制方程式(33)得到下列线性边值问题:
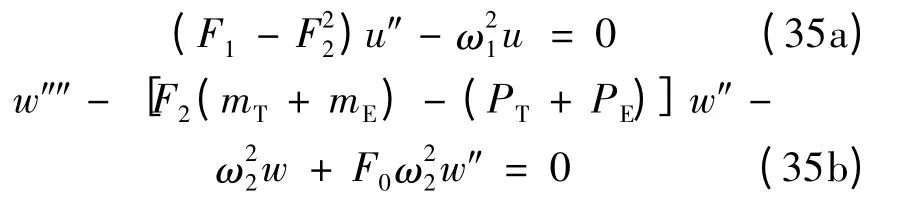
pinned-pinned:
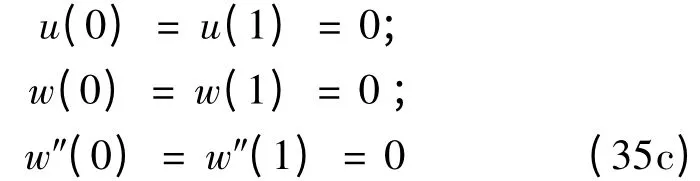
fixed-fixed:
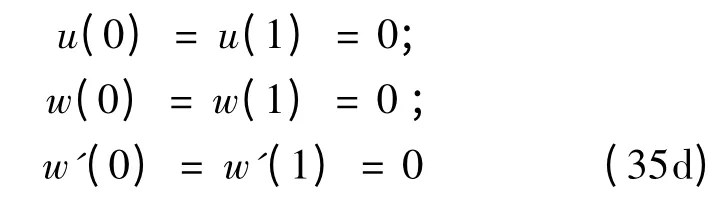
3 结果与讨论
为了满足u 的边界条件,假设u = Asinnπξ,代入控制方程式(35a),得到梁纵向振动的各阶固有频率的解析表达式:
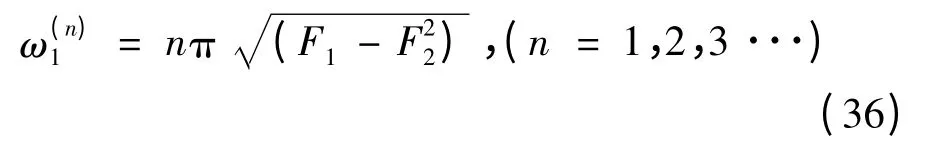
纵向振动的一阶固有频率为:
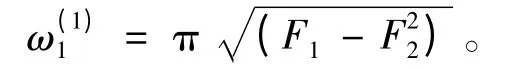
为验证结果的正确性,将贴压电层的功能梯度材料梁退化到各向同性材料(无压电,功能梯度参数)时,n = 0,F2= 0,F1= 12δ2,此时ω(n)1= nπ与文献[24]中的结果相同。
当梁的两端简支pinned-pinned 时,w = Bsinnπξ满足相应的边界条件,代入方程式(35b),由B ≠0可得特征方程:
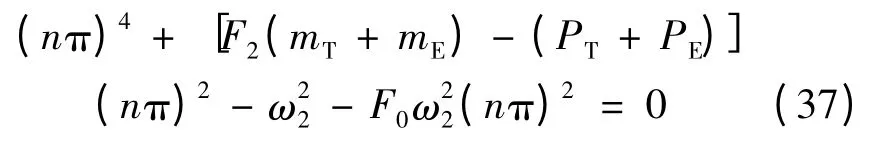
从而求得系统横向振动频率
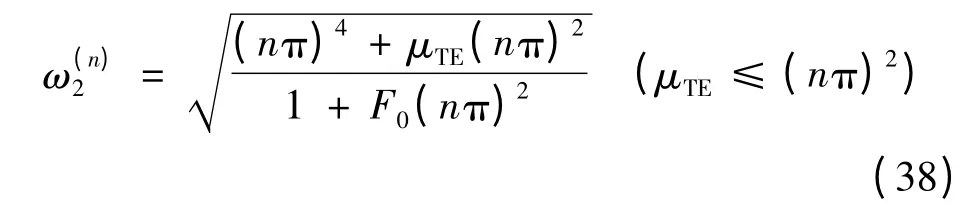
其中:μTE= F2(mT+ mE)- (PT+ PE)。
由梁的热弹性稳定性分析可知,μ(n)= (nπ)2是对应于pinned-pinned 梁的热屈曲各阶失稳模态的载荷特征值(无量纲升温)。n = 1 时得到临界升温μcr= μ(1)= π2,于是式(38)可以表示为:
如果退化到均匀(陶瓷)材料,则m1= m2= 0;PE= 0;mE= 0;n = 0 ;F1=12δ2,F2= 0 ,F0=1/12δ2,PT= 12δ2αcT,于 是 得 到:=则与横向振动频率的表达式其中μ = 12δ2αcT,r2= 1/12δ2比较,可以看出在均匀升温下两者的表达式是完全一样的。
对于fixed-fixed 梁,选取满足相应横向边界条件的近似的一阶振型函数:

利用Galerkin 法[5,13],可以得到梁的一阶近似固有频率
对于其他低阶固有频率则考虑打靶法[17~19]求解,计算中,考虑梁的中间层为陶瓷氧化锆(Zirconia/ZrO2)和金属铝(Aluminum/Al)两相材料制成的功能梯度材料(记为ZrO2/Al),上、下表层压电材料为G-1195N。材料物性参数见表1[9,10]。

表1 压电-功能梯度层合梁的物性参数Table 1 Material property parameters of the piezoelectric FGM beams
为了验证上述理论分析和计算程序的正确性,在将压电-功能梯度梁退化为均匀各向同性梁的情况下(n = 0 ,η = 0 )的所得数值结果与已有结果进行了比较。在均匀升温情况下(Tr= 1 ),表2 中给出由本工作所计算获得的无量纲临界屈曲温度τcr= 12δ2αcTcr与文献[17]中结果的比较。可以看出,两者吻合较好。
对于控制方程(35b)和边界条件(35d),利用打靶法把边值转化为初值问题求解,退化到无压电,均匀材料,均匀升温情况下,求得在临界温度附近的其他低阶固有频率:

表2 具有不同长细比梁的无量纲临界升温值Table 2 Critical non-dimensional thermal of beams with aspect radio δ
由频率的表达式(39),(42)知,对于细长梁,截面转动惯量(含在F0里)对横向振动频率可以忽略,在不考虑升温、压电情况下,表3 给出了细长比δ 为不同值时,考虑转动惯性力时的一阶固有频率与忽略转动惯性力时的一阶频率的比值,由此可见转动惯性力对频率的影响程度。
表3 转动惯性力对振动频率值比的影响(PT,PE,MT,ME = 0 )Table 3 Effects of inertia forces to natural frequencies
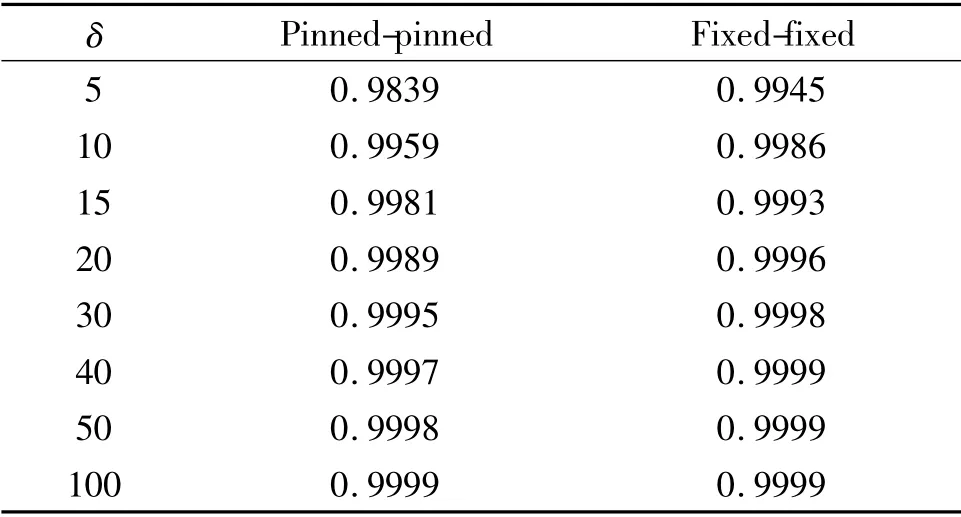
表3 转动惯性力对振动频率值比的影响(PT,PE,MT,ME = 0 )Table 3 Effects of inertia forces to natural frequencies
δ Pinned-pinned Fixed-fixed 5 0.9839 0.9945 10 0.9959 0.9986 15 0.9981 0.9993 20 0.9989 0.9996 30 0.9995 0.9998 40 0.9997 0.9999 50 0.9998 0.9999 100 0.9999 0.9999
表4 ~表7 给出了固支条件下,不同载荷参数、不同材料参数情况下,FGM 层合梁在临界载荷附近的其他低阶固有频率。
4 结论
(1)梁纵向振动频率只与材料的性质有关,与电压升温都没有关系,这是因为温度场和电场都是横向的,对纵向振动没有影响。
(2)当上下压电层电压同向时,升压都会降低梁横向振动的频率;当上下压电层电压异向时,升压都会增大梁横向振动频率。

表4 在参数η = 0,Tr = 1,δ = 30 一定的情况下其他低阶固有频率Table 4 The other natural frequencies when parameters η = 0,Tr = 1,δ = 30 are given

表5 在参数λ = 0,Tr = 1,δ = 30 一定的情况下其他低阶固有频率Table 5 The other natural frequencies when parameters λ = 0,Tr = 1,δ = 30 are given

表6 在参数n = 0,Tr = 5,δ = 30 一定的情况下其他低阶固有频率Table 6 The other natural frequencies when parameters n = 0,Tr = 5,δ = 30 are given

表7 在参数λ = 0,Tr = 5,δ = 30 一定的情况下其他低阶固有频率Table 7 The other natural frequencies when parameters λ = 0,Tr = 5,δ = 30 are given
(3)升温只会降低梁的固有频率;温度场非均匀程度也会影响结构的固有频率。
(4)通过对上下压电层的反向驱动(Φ <0 ),可以减小甚至抵消掉升温引起的自振频率的变化,实现对结构的固有频率的调节。
[1]CEAWLEY E F,de LUIS J. Use of piezoelectric actuators as elements of intelligent structures[J]. AIAA Journal,1987,25(10):1373 -1385.
[2]ZHOU Y H,WANG J Z. Vibration control of piezoelectric beam-type-plates with geometrical nonlinear deformation[J]. Int J Non-Linear Mech,2004,39:909 -920.
[3]XIA X K,SHEN H S. Vibration of postbuckled FGM hybrid laminated plates in thermal environment[J]. Engineering Structures,2008,30(9):2420 -2435.
[4]丁丽霞,刘玮. 压电元件驱动的功能梯度弹性薄板的屈曲[J]. 功能材料,2006,37(8):1229 -1238.(DING L X,LIU W. The buckling analysis of functionally gradient thin elastic plate bonded piezoelectric patches[J].Journal of Functional Materials,2006,37(8):1229 -1238.)
[5]DAI K Y,LIU G R ,HAN X,et al. Thermo-mechanical analysis of functionally graded material (FGM)plates using element-free Galerkin method[J]. Computers and Structures,2005,83:1487 -1502.
[6]林启荣,刘正兴,王宗利.电场作用下压电层合梁的分析[J].应用数学和力学,2001,22 (9):969 -975.(LIN Q R,LIU Z X,WANG Z G. Analysis of beams with piezoelectric actuators[J]. Applied Mathematics and Mechanics,2001,22(9):969 -975.)
[7]FRIDMAN Y,ABRAMOVICH H. Enhanced structural behavior of flexible laminated composite beams[J].Composite Structures,2008,82 :140 -154.
[8]SHEN H S. Postbuckling of FGM plates with piezoelectric actuators under thermo-electro-mechanical loadings[J]. Int J of Solids and Structures,2005,42:6101 -6121.
[9]SHEN H S. Post-buckling of shear deformable laminated with piezoelectric actuators under complex loading conditions[J]. Int J of Solids and Structures,2001,38:7703 -7721.
[10]HUANG X L,SHEN H S. Vibration and dynamic response of functionally graded plates with piezoelectric actuators in thermal environments[J]. Journal of Sound and Vibration,2006,289(1/2):25 -53.
[11]ANNIGERI A R,GANESAN N,SWARNAMANI S. Free vibration behaviour of multiphase and layered magneto-electro-elastic beam[J]. Journal of Sound and Vibration,2007,299 :44 -63.
[12]RAJESH K,BHANGALE,GANESAN N. Free vibration studies of simply supported non-homogeneous functionally graded magneto-electro-elastic finite cylindrical shells[J].Journal of Sound and Vibration ,2005,288:412 -422.
[13]YANG J,KITIPORNCHAI S,LIEW K M. Large amplitude vibration of thermo-electro-mechanically stressed FGM laminated plates[J]. Comput Methods Appl Mech Engrg,2003,192:3861 -3885.
[14]于涛,仲政.功能梯度压电悬臂梁的弯曲分析[J].中国科学:物理学 力学 天文学,2006,36(5):518 -529.(YU T,ZHONG Z. Bending analysis of a functionally graded piezoelectric cantilever beam[J]. Scientia Sinica:Physica,Mechanica & Astronomica,2006,36(5):518 -529.)
[15]丁皓江,徐荣桥,国风林. 轴对称层合横观各向同性压电圆板的精确解[J]. 中国科学:技术科学,1999,29(3):214 -221.(DING H J,XU R Q,GUO F L.Exact solution of axisymmetric laminated transversely isotropic piezoelectric circular plate[J]. Scientia Sinica:Technologica,1999,29 (3):214 -221.)
[16]丁皓江,陈伟球,徐荣桥. 压电板壳自由振动的三维精确分析[J].力学季刊,2001,22 (1):1 -9.(DING H J,CHEN W Q,XU R Q. Three-dimensional exact analyses of free vibrations for piezoelectric plates and shell[J]. Chinese Quarterly of Mechanics,2001,22(1):1 -9.)
[17]LI S R,ZHANG J H,ZHAO Y G. Thermal post-buckling of functionally graded material timoshenko beams[J]. Applied Mathematics and Mechanics (English Edition),2006,27(6):709 -715.
[18]LI S R,SU H D,CHENG C J. Free vibration of functionally graded material beams with surface-bonded piezoelectric layers in thermal environment[J]. Applied Mathematics and Mechanics(English Edition),2009,30(8):1 -14.
[19]苏厚德,李世荣,高颖. 粘贴压电层功能梯度材料Timoshenko 梁的热过屈曲分析[J]. 计算力学学报,2010,27(6):1067 -1072.(SU H D,LI S R,GAO Y,Thermal post-buckling of functionally graded material timoshenko beams with surface-bonded piezoelectric layers[J]. Chinese Journal of Computational Mechanics,2010,27 (6 ):1067 -1072. )

