宽带频率－方向不变恒定主瓣波束形成

苏成晓 罗景青 刘颂阳

（1.解放军电子工程学院雷达对抗系，合肥，230037；2.吉林大学仪器科学与电气工程学院，长春，130061）

引 言

宽带信号处理中，为了保证信号通过基阵系统后频率特性不发生畸变，要求波束主瓣宽度不随频率发生变化，即满足频率不变特性。频率不变波束形成主要有最小二乘法［1－2］和空 间重采 样法［3］，此外还有一些优化逼近算法［4－5］，约束设计波束与参考波束误差最小，优化求解得到权向量。对于常规宽带波束形成，主瓣宽度不仅随频率变化，而且随着波束指向变化，当波束指向逐渐偏离基阵法线方向时，主瓣逐渐变宽［6］，这势必导致阵列分辨性能下降。

为保证阵列的指向性能不变，要求波束在不同指向上始终保持主瓣恒定，即实现方向不变特性。文献［6］将研究局限于均匀线阵，无法适用于任意阵型阵列。文献［7，8］采用在波束的主、旁瓣区域内设置虚拟干扰源的方式，通过调整干扰源强度控制波束的主旁瓣，该方法计算量与干扰源数目成正比，而干扰源数目偏少会影响算法效果。到目前为止，对于方向不变波束的研究较少，而且针对的都是窄带情况。

为了实现宽带波束频率和方向上的二维主瓣恒定，本文基于约束优化的方法，分别在频率和方向上进行主瓣恒定约束，并用二阶锥规划求解最优权向量。相对于频率不变波束，采用频率－方向不变波束的宽带信号到达角（Direction of arrival，DOA）估计，信号的分辨概率和估计性能得到提升。

1 问题描述

宽带频域波束形成通常将带宽划分为若干个不重叠的子带，然后每个子带分别利用窄带方法形成波束。假设阵元个数为L，第j个子带中心频率为fj，阵列方向向量为a（fj，θ），加权向量为WH（fj，θm），θm表示波束指向，则频率fj处指向为θm的波束方向图函数为

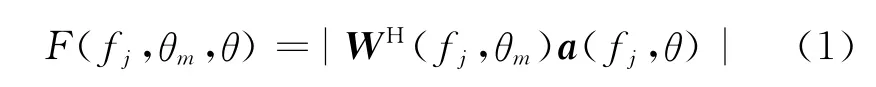
从式（1）可以看出，波束方向图函数与频率fj和波束指向θm有关。只考虑频率的影响，假设参考频率f0处指向为θm的波束主瓣角度范围Θm，为了实现不同频率波束主瓣恒定，对于带宽内任意频率fj和主瓣内任意角度θ∈Θm，不同频率处加权向量须满足

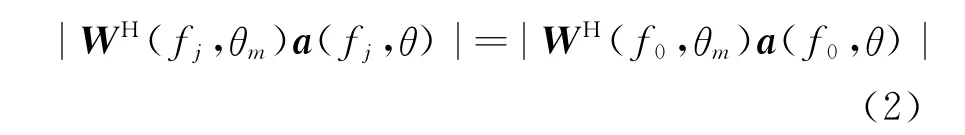
对于指向分别为θm1，θm2的两个波束，假设θm2－θm1＝θI，θm1处主瓣角度范围为Θm1，θm2处主瓣角度范围为Θm2。为了实现不同指向波束主瓣恒定，对于任意两个波束指向θm1，θm2和任意角度θ∈Θm1，不同指向处加权向量须满足

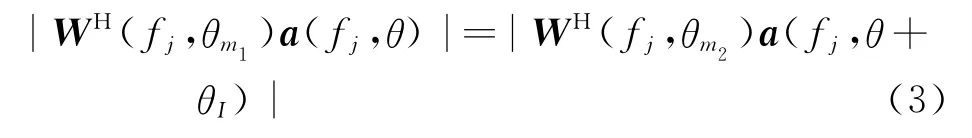
式（2，3）分别给出了频率不变和方向不变恒定主瓣波束形成加权向量需要满足的条件。对于宽带波束形成，要使波束在频率和方向上均实现主瓣恒定，则对于带宽内任意频率fj和主瓣内任意角度θ∈Θm1，加权向量须满足

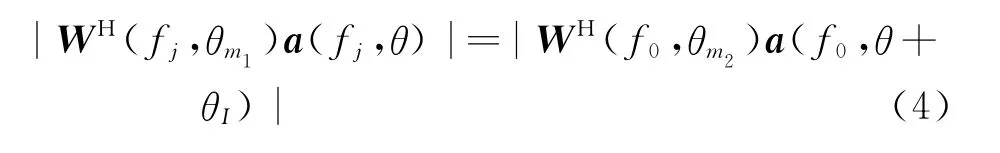
2 频率－方向不变恒定主瓣波束形成

实现频率－方向不变恒定主瓣波束，关键是加权向量的求解。本文采用约束优化方法，设计出满足要求的波束，并将问题表示为二阶锥规划［9］的形式，使用SeDuMi工具箱求解全局最优权向量。

2.1 频率不变主瓣恒定约束

单纯考虑波束指向θm处频率不变恒定主瓣波束形成，下列表达式中略去θm。假设频率fj处设计波束为F（fj，θ），参考波束为频率f0处波束F（f0，θ），波束主瓣区域为ΘML，旁瓣区域为ΘSL，θp∈ΘML（p＝1，2，…，P）和θq∈ΘSL（q＝1，2，…，Q）分别为主瓣和旁瓣离散化的方位点。频率不变主瓣恒定约束的核心思想是：在保证设计波束与参考波束主瓣幅度误差小于某期望值的条件下，使设计波束旁瓣级最低，即满足约束

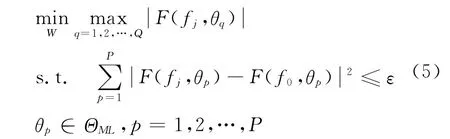
式中：ε确定了设计波束与参考波束主瓣幅度误差平方和的上限。如果fj取遍整个信号带宽，就可以在不同频率处获得具有同样主瓣的波束图，实现频率不变恒定主瓣波束形成。

2.2 方向不变主瓣恒定约束

单纯考虑频率fj处方向不变恒定主瓣波束形成，下列表达式中略去fj。假设参考波束指向为θ0，主瓣范围记为Θ0，波束函数记为F（θ0，θ），设计波束主瓣指向θm，波束函数记为F（θm，θ），主瓣范围记为Θm，旁瓣记为Θs。由主瓣恒定可知，Θm实际为Θ0整体向右平移θm－θ0度。设θk∈Θm（k＝1，2，…，K）和θr∈Θs（r＝1，2，…，R）分别为设计波束主瓣和旁瓣区域离散化的方位点。方向不变恒定主瓣约束的核心思想是：在保证设计波束与参考波束主瓣之间的幅度误差最小的条件下，使设计波束旁瓣级最低，即满足约束

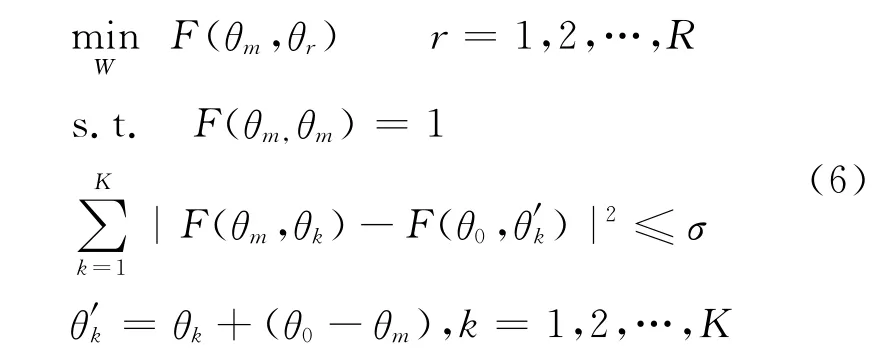
式中：σ确定了设计波束与参考波束主瓣幅度误差平方和的上限。如果θm取遍整个观察区域，就可以在不同波束指向处获得具有同样主瓣的波束图，实现方向不变恒定主瓣波束形成。

实际上，离散化方位点的位置和数目对于频率不变和方向不变主瓣恒定约束都是有影响的。一般情况下在主瓣区域和旁瓣区域平均离散化采样点，保证在波束各个位置形成约束。离散点的数目越多，约束越精确，但计算量也随之增大，因此在实际运算中，可以根据需要合理选择离散点数目。

2.3 频率－方向不变波束形成算法

频率－方向不变恒定主瓣波束形成的思想是：首先实现参考频点的方向不变恒定主瓣波束，然后用参考频点处各个指向的波束作为相应方向上的参考波束，实现频率不变恒定主瓣波束。算法步骤概括为：

（1）子带分解，选取参考频率f0以及参考波束指向θ0；

（2）以频率f0处指向θ0的波束作为参考波束，利用式（6）约束条件在观测区域各个波束指向上实现方向不变主瓣恒定；

（3）以f0处相应指向的方向不变波束作为参考波束，利用式（5）约束条件在信号带宽各个频率上实现频率不变主瓣恒定。

约束优化利用SeDuMi工具箱求解。在Se－DuMi工具箱中，标准的凸优化问题定义为

式中：b和c为任意向量，A为任意的系数矩阵，y为包含有未知参数的向量，而κ为一个对称锥的集合。以频率不变主瓣恒定约束为例，引入一新的非负变量δ和一组非负变量εp（p＝1，2，…，P），式（5）可以转化为

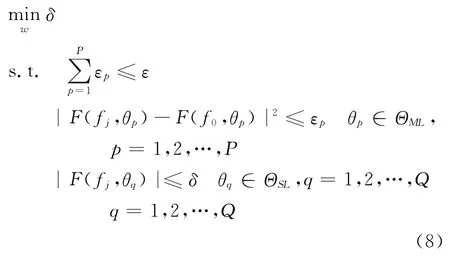
定义y＝［δ，ε1，ε2，…，εP，WT（fj，θm）］T，b＝［－1，01×P，01×L］，则－δ＝bTy。式（8）的第一个约束可以表示为

式中：R＋表示非负实数集合。式（8）的第2个约束可以表示为

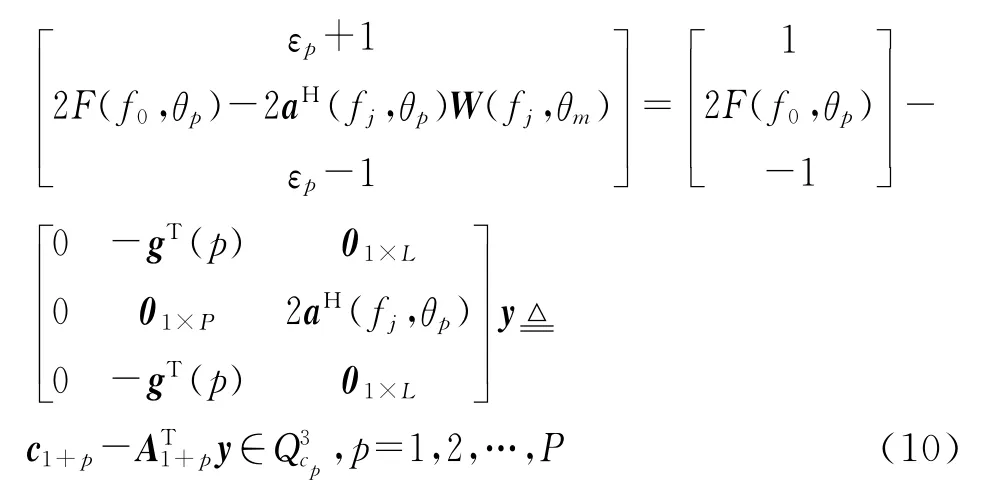
式中：g（p）＝ ［g1，g2，…gi，…，gP］T且gi＝式（8）的第3个约束可以表示为

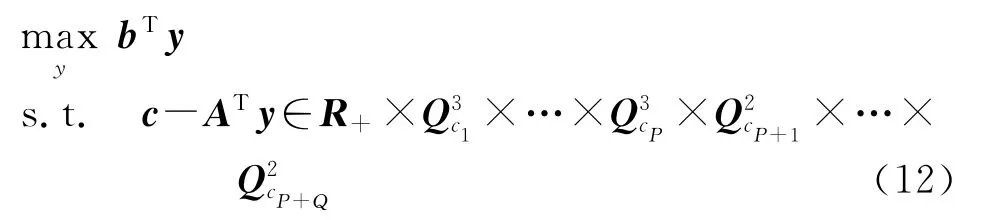
利用SeDuMi求解得到y的最优解后，取其后L个分量即得到加权向量。对式（6）的方向不变主瓣恒定约束，同样可以利用类似的方法，将之表示为二阶锥规划形式进行求解。

3 基于频率－方向不变波束的DOA估计

频率－方向不变波束对于宽带波束形成、宽带多波束测向以及合成孔径雷达成像等都具有实际意义。文献［10］最早将频率不变波束用于宽带信号DOA估计，但频率不变波束在不同波束指向时主瓣宽度是变化的，这势必影响到算法的性能。下面将本文提出的宽带频率－方向不变波束应用到宽带信号DOA估计中。

考虑L元阵列，空间接收D个远场宽带信号，方向记为ΘD，阵列接收数据为

式中：A（fj，Θ）为阵列流形，S（fj）为fj处频域信号，N（fj）为频域噪声向量，假定为高斯白噪声。空间形成M个频率－方向不变波束，波束指向分别为θm，m＝1，2，…，M，则M个波束的输出为

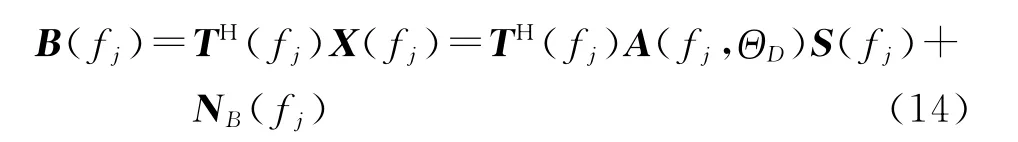
式中：T（fj）＝［W（fj，θ1），W（fj，θ2），…，W（fj，θM）］表示M个频率－方向不变波束在频率fj处的波束形成矩阵，NB（fj）＝TH（fj）N（fj）。波束形成矩阵满足

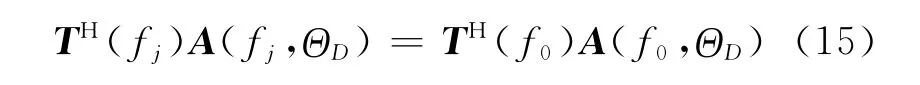
经过波束形成矩阵，阵元域的数据变换到波束域，同时实现了聚焦，所有频率数据变换到了参考频率f0上，方向向量变为b（f0，θ）＝TH（f0）a（f0，θ）。与频率不变波束不同，波束形成矩阵T（fj）形成的M个不同指向的波束主瓣宽度是一致的。波束输出的协方差矩阵为

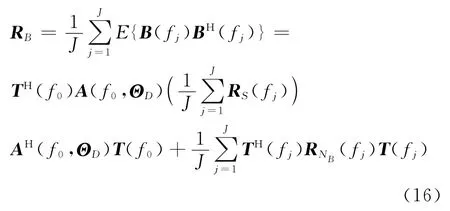
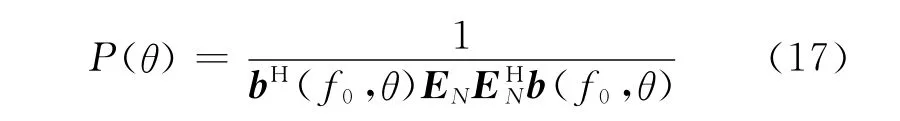
谱峰位置对应于信号的来波方向。

4 仿真实验

4.1 频率－方向不变恒定主瓣波束形成

假设16元均匀线阵，信号频率范围为1.2～1.4GHz，阵元间距为最大频率对应波长的一半。选取频率1.3GHz，指向为0°的均匀加权波束为参考波束，信号带宽划分为J＝20个子带，每个子带带宽为10MHz。图1为只考虑频率不变主瓣恒定约束时指向为20°的波束图；图2为只考虑方向不变主瓣恒定约束时参考频点处的波束图；图3为指向分别为－40°、20°时频率－方向不变波束图；图4为主瓣宽度随波束指向变化曲线。

图1（a，b）分别为频率不变波束的立体图和平面图，由图可知，频率不变主瓣恒定约束能够在信号频率范围内保持主瓣恒定。图2（a，b）分别为参考频率处方向不变波束的立体图和俯视图，由图可知，方向不变主瓣恒定约束能够在不同波束指向时保持主瓣恒定。图3（a，b）分别为频率－方向不变波束形成的立体图和俯视图。－40°，20°指向波束主瓣宽度相同，而且这两个指向处的波束均能实现频率不变主瓣恒定。

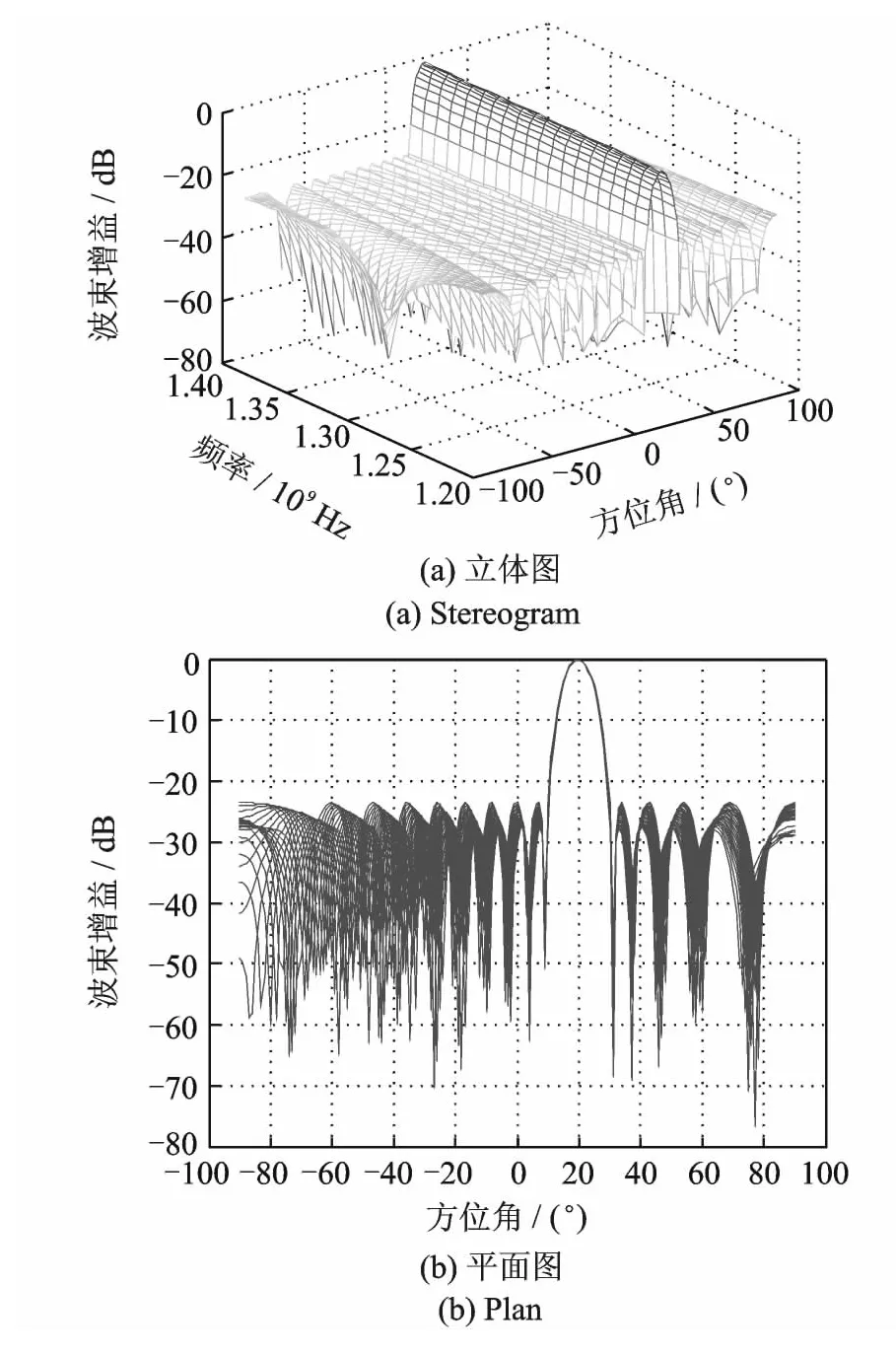
图1 指向20°时频率不变波束Fig.1 Frequency invariant beam on 20°

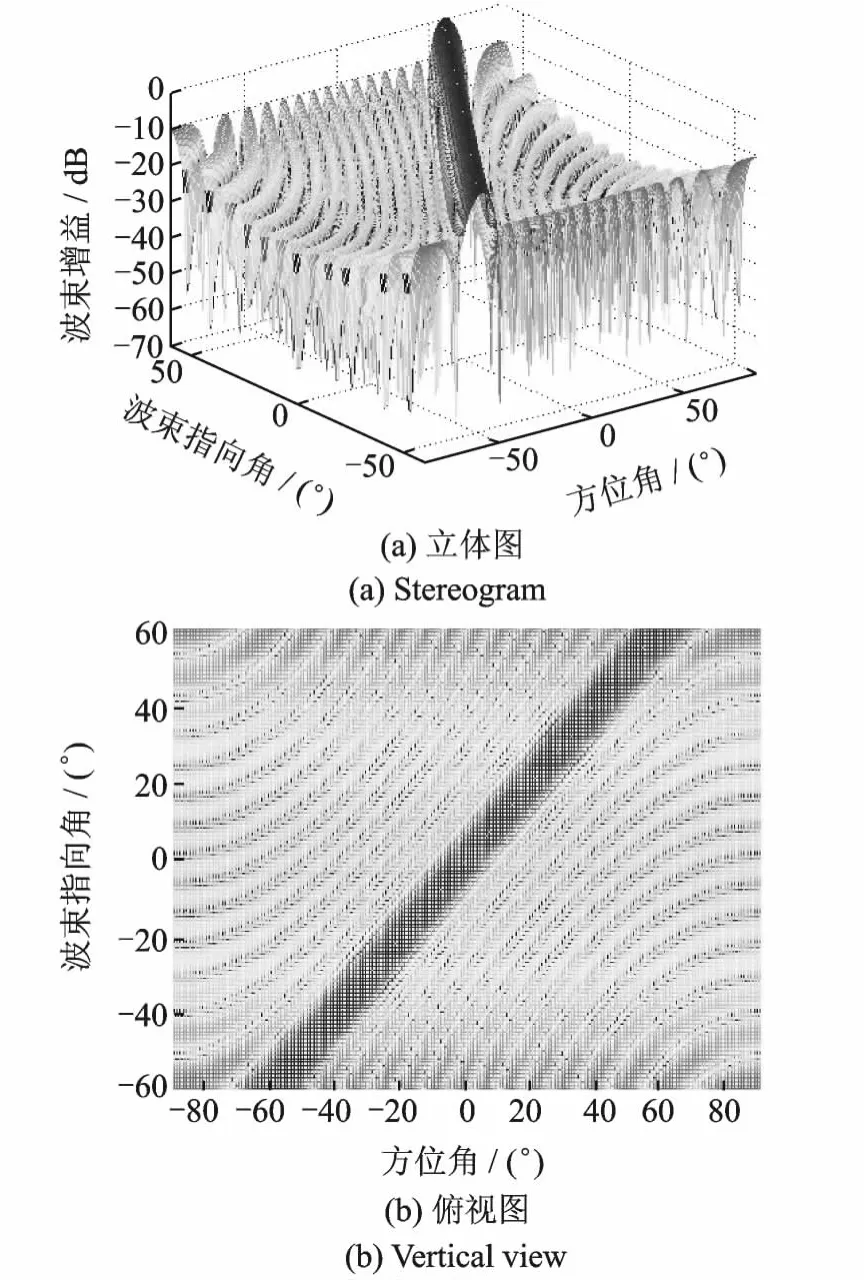
图2 参考频率处方向不变波束Fig.2 Steering invariant beam on reference frequency

图3 频率－方向不变波束Fig.3 Frequency－steering invariant beam

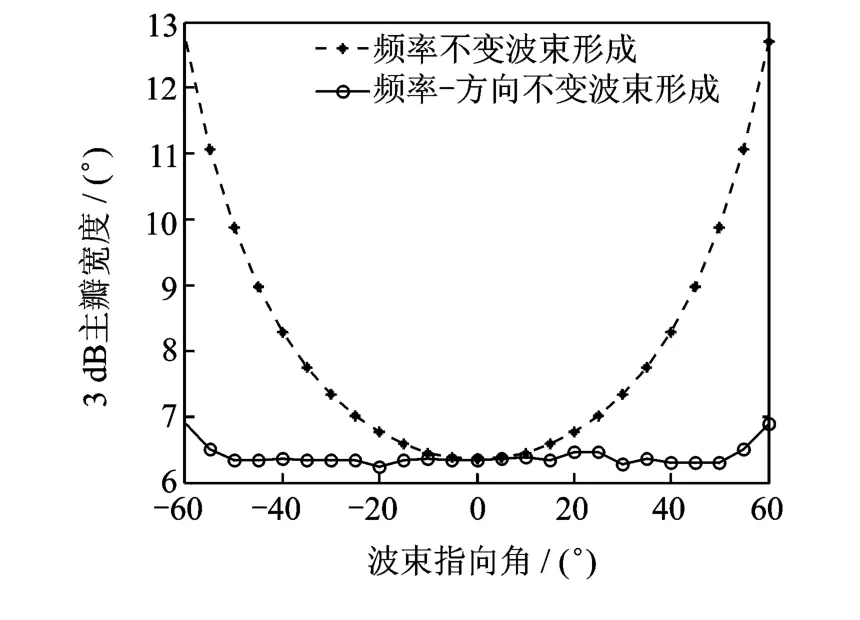
图4 主瓣宽度随波束指向变化曲线Fig.4 Curve of beam－width versus mainlobe direction

图4中两条曲线分别表示频率不变波束和频率－方向不变波束主瓣宽度随波束指向变化曲线。随着波束指向偏离阵列法线方向，频率不变波束的主瓣宽度随之增大，而频率－方向不变波束能够在±50°范围内保持主瓣宽度基本不变。

4.2 基于频率－方向不变波束的DOA估计

考虑4.1节中阵列，空间两等功率远场宽带信号，来波方向分别为18°，22°，采样频率为512MHz，观测时间为20μs，数据分为16段，将信号带宽分为20个子带，选取参考频率1.3GHz，指向为0°，旁瓣电平为－30dB的切比雪夫加权波束作为参考波束，空间形成3个频率－方向不变波束，波束间－3dB交叠，波束指向分别为12°，20°，28°。图5为信噪比5dB时进行200次蒙特卡罗实验谱估计结果，图6为DOA估计性能与信噪比关系曲线。

图5为采用频率－方向不变波束的宽带波束域DOA空间谱估计结果。由图可知，两信号得到正确分辨和估计，说明频率－方向不变波束用于宽带信号DOA估计中的有效性。

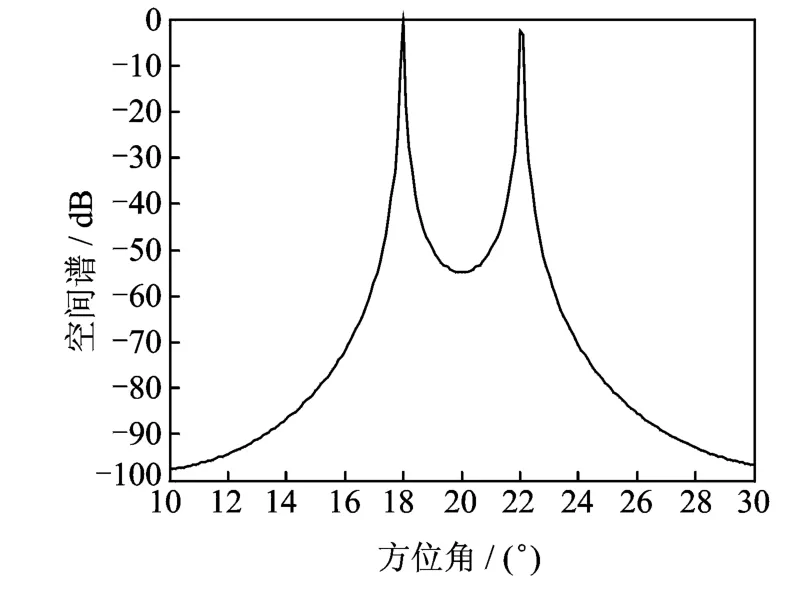
图5 空间谱估计曲线Fig.5 Spatial spectrum estimation curve

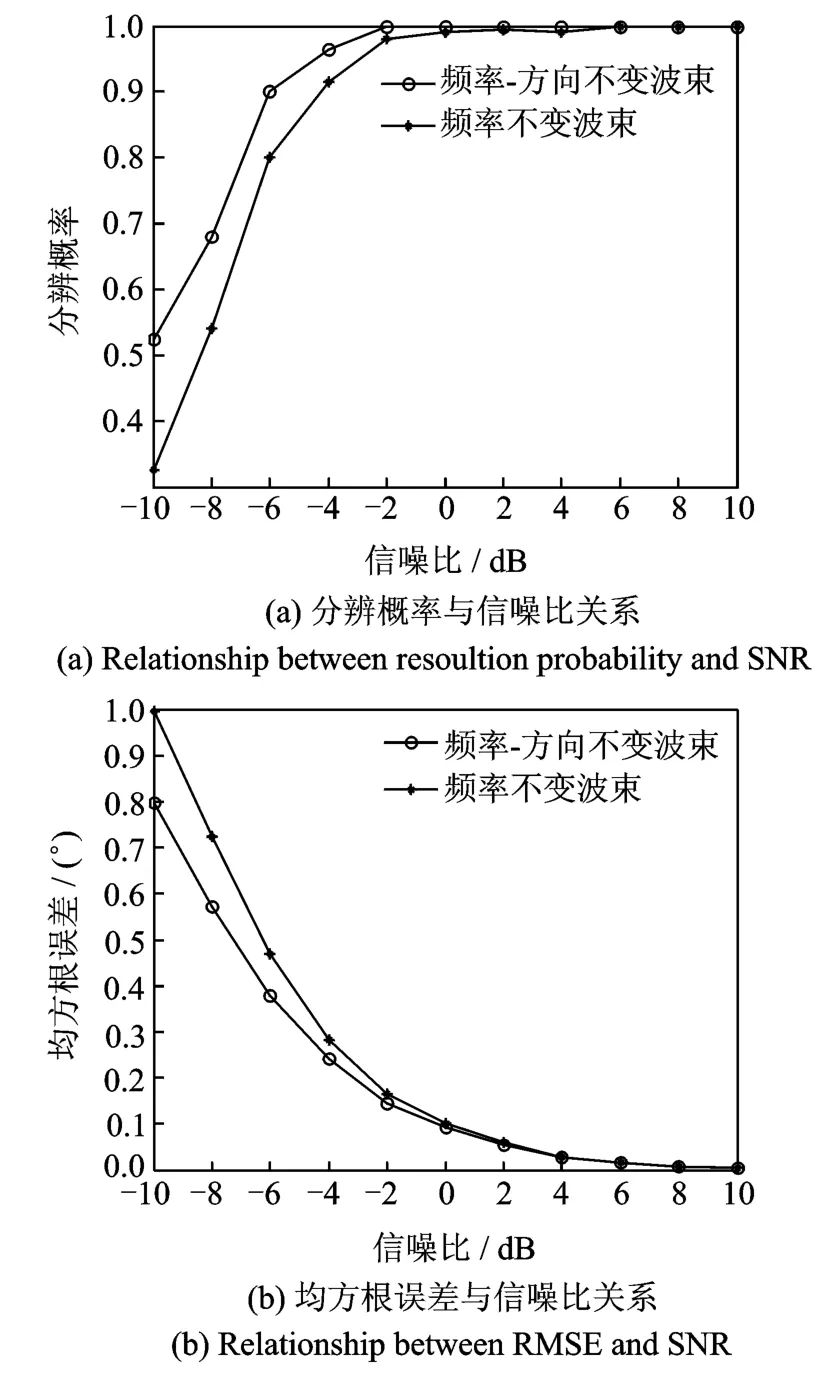
图6 算法性能与信噪比关系曲线Fig.6 Curve of algorithm performance versus SNR

图6为分别采用频率－方向不变波束和频率不变波束时，宽带信号DOA估计性能与信噪比关系曲线。图6（a）为分辨概率与信噪比关系曲线，由图可知，同一信噪比条件下，采用频率－方向不变波束，分辨概率要优于频率不变波束。图6（b）为均方根误差与信噪比关系曲线，由图可知，同等信噪比条件下，采用频率－方向不变波束，均方根误差小于采用频率不变波束，这是因为3个频率－方向不变波束主瓣宽度与0°方向波束主瓣宽度相同，相当于在偏离阵列法线方向上增大了阵列孔径。

5 结束语

本文提出了一种宽带频率－方向不变恒定主瓣波束形成算法，并将之应用到宽带信号DOA估计中。运用约束优化的方法，分别对频率不变主瓣恒定和方向不变主瓣恒定进行约束，并表示为标准二阶锥规划的形式进行求解。实验表明，提出的频率－方向不变波束形成算法能够实现不同频率不同波束指向主瓣恒定，与频率不变波束相比，采用频率－方向不变波束的DOA估计方法降低了信噪比分辨门限，提高了估计精度。

［1］Zhao Y，Liu W，Langley R.Application of the least squares approach to fixed beamformer design with frequency－invariant constraints［J］.IET Signal Processing，2011，5（3）：281－291.

［2］Zhao Y，Liu W，Langley R.Adaptive wideband beamforming with frequency invariance constraints［J］.IEEE Transactions on Antennas and Propagation，2011，59（4）：1175－1184.

［3］王杰贵，罗景青.一种恒定束宽的宽带数字波束形成方法［J］.宇航学报，2007，28（6）：1458－1461.Wang Jiegui，Luo Jingqing.A novel constant beamwidth digital beamforming method ［J］.Journal of Astronautics，2007，28（6）：1458－1461.

［4］Wei Liu，Des C M，Mounir G.Design of frequency invariant beamformer without temporal filtering［J］.IEEE Transaction on Signal Processing，2009，57（2）：798－802.

［5］Xie N，Wang H，Liu H.Broadband frequency invariant beamformer［J］.Wireless Personal Communications，2010，61（1）：1－17.

［6］Khanna R.Characterization and development of algorithms for arrays processing architectures of adaptive antennas in wireless communication［D］.India：Deemed University，2006.

［7］幸高翔，蔡志明.旁瓣约束方向不变恒定束宽波束自适应综合［J］.声学技术，2009，28（2）：172－175.Xing Gaoxiang，Cai Zhiming.Synthesis of adaptive steering－invariant constant－beamwidth pattern with sidelobe constraints［J］.Technical Acoustics，2009，28（2）：172－175.

［8］幸高翔，蔡志明.方向不变恒定束宽波束图数值综合［J］.电子与信息学报，2009，31（3）：574－577.Xing Gaoxiang，Cai Zhiming.Numerical systhesis for constant beamwidth beam pattern with steering－invariance［J］.Journal of Electronics ＆ Information Technology，2009，31（3）：574－577.

［9］丁淑娟，刘子龙，孙广俊，等.线性调频信号数字脉压滤波器优化设计［J］.数据采集与处理，2012，27（5）：602－606.Ding Shujuan，Liu Zilong，Sun Guangjun，et al.Digital pulse compression filter optimization design for LFM signal［J］.Journal of Data Acquisition and Processing，2012，27（5）：602－606.

［10］Lee T S.Efficient wideband source localization using beamforming invariance technique［J］.IEEE Transactions on Signal Processing，1994，42（6）：1376－1387.