基于可信度的加权协作频谱检测算法
王海莲 张士兵 郭莉莉
(南通大学电子信息学院,南通,226019)
引 言
随着无线通信技术的快速发展,频谱需求不断增长和频谱资源日益紧缺之间的矛盾越来越突出。作为提高无线频谱利用效率的革命性技术手段,认知无线电(Cognitive radio,CR)技术从多维空间的角度实现了对空闲频谱的动态使用,被公认为是智能感知频谱环境、高效利用无线频谱资源的技术手段之一,引起了人们的广泛关注[1]。频谱检测[2]技术是认知无线电核心技术之一,实时、可靠地检测频谱的使用状况是频谱检测的基本任务。
现有的频谱检测主要有能量检测(Energy detector,ED)、匹配滤波器检测(Matched filtering,MF)和循环平稳特征检测(Cyclostationarity-based sensing,CS)[3],其中 ED 是常用的方法,但是 ED对微弱信号的检测能力较差且易受噪声不确定性的影响。针对ED方法存在的不足,近年来,人们将随机矩阵理论应用到频谱感知中,通过接收信号协方差矩阵的最大最小特征值设计频谱检测的特征量与频谱判决门限[4-6]。Zeng等利用大维随机矩阵理论从单个认知用户的角度研究了最大最小值特征值算法(Maximum-minimum eigenvalue detector,MMED)[4],MMED克服了ED算法中噪声不确定性的问题,提高了噪声波动环境下的频谱检测性能。在实际无线通信场景中,单节点检测方案易受衰落、多径、隐藏终端等因素影响,降低检测性能。协作频谱检测是解决上述问题的有效方法[3,7]。
协作频谱检测可以改善系统检测的性能,但是现有的协作融合规则没考虑到各节点所处环境差异导致各节点感知可靠度不同。为进一步提高频谱检测的可靠性,提出基于信任度加权的协作频谱感知算法[8-13]。加权协作频谱检测中,每个感知节点先进行本地检测,融合中心(Fusion center,FC)根据不同的信道条件赋予每个感知节点不同的权重值来确定对全局检测的贡献,从而提高检测性能。例如基于信噪比的加权(Weighted cooperative spectrum sensing,WCSS)[8-10]给高信噪比信道赋予较大的权重值,要求每个感知节点必须估计检测信道的信噪比;基于检测概率的加权[12-13]是给高检测概率的用户分配较大的权重值,这种方法需要感知节点必须估计到每个信道的检测概率,而在实际应用中这些先验信息较难得到。
本文在分析现有的协作频谱检测算法的基础上,结合无线电通信环境的实际情况,考虑到不同感知节点的本地检测结果的可信度不同,提出一种基于可信度的加权协作频谱检测算法(Weighted cooperative spectrum sensing algorithm based on reliability,WCSA)。在该算法中,每个感知节点利用MMED算法获得本地检测结果和检测统计量;根据每个感知节点的历史行为更新各节点本地检测结果的可信度。利用切尾平均法计算可信度门限,选择可信度大于可信度门限的感知节点参与协作,并根据每个感知节点的可信度大小赋予它们的检测统计量不同的加权值。仿真结果表明,该算法提高了频谱检测性能,有效克服噪声不确定性,通过设置可信度门限在保证检测性能指标的前提下减少参与协作的用户数,有效降低了系统协作检测的复杂性。
1 系统模型及本地检测算法
假设认知无线电网络中有一个主用户(Primary user,PU),M个感知节点(Secondary users,SU),如图1所示。每个SU独立的进行频谱检测并把本地频谱检测结果或者检测数据发送给FC,FC融合感知节点的本地检测信息并做出最终判决。

图1 认知无线电网络示意图Fig.1 Model of cognitive radio network
对于SUi(i=1,2,…,M),通过N个抽样向量Xi(n)(n=1,…,N)检测PU是否存在。每个抽样向量Xi(n)由L(过采样因子)个连续抽样构成,即Xi(n)=[x1(n),…,xL(n)]T,其中(·)T表示转置变换,每次检测共抽样L·N个样值。SUi通过对接收信号的观测,确定PU信号是否存在。该问题可以归纳为一个二元假设检验问题,即

式中:H0表示PU信号不存在时的假设,H1表示存在PU信号时的假设。Si(n)表示SUi接收到的PU信号向量,Vi(n)表示均值为0、方差为独立同分布的加性高斯白噪声。
定义Si(n),Xi(n)的统计协方差矩阵分别为Rs=E(SSH),Rx=E(XXH),其中(·)H表示转置变换,Si(n)和Vi(n)相互独立,则统计协方差矩阵Rx在H0和H1两种假设条件下可表示为

式中I表示单位矩阵。在实际应用中,统计协方差矩阵无法准确地计算出来,只能获得有限的抽样( )N估计协方差矩阵
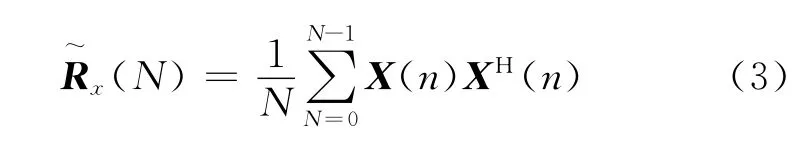
设λmin和λmax分别为(N)的最小和最大特征值,ρmin和ρmax分别为Rs(N)的最小和最大特征值。当PU信号不存在时ρmin=ρmax=0,则λmin=λmax,即λmax/λmin=1;而当PU信号存在时,λmax>λmin,即λmax/λmin>1。因此可以利用T=λmax/λmin作为检测统计量来检测主信号是否存在情况。对于给定的判决门限γ,有

在实际应用中,通常基于频谱检测虚警率(Pfa)研究感知算法。在H0假设情况下,采样协方差矩阵( )N(节点采样数N足够大)是个特殊的 Wishart矩阵[14],运用随机矩阵理论和Tracy-Widom及其数值表[4]可以得到判决门限

2 基于可信度的频谱检测算法
2.1 可信度因子
为了真实反映感知节点频谱检测的准确性,本文引入可信度因子。系统初始状态时,无法对参与协作的感知节点的感知能力进行判断,但是随着感知系统的不断感知,可以通过参考每个感知节点的历史感知情况,对每个感知节点的感知可靠程度进行估计。融合中心在做出最终判决时,对各感知节点进行可信度加权,提高频谱检测结果的正确性。可信度因子通过比较融合中心检测结果与本地检测结果的一致性来确定,感知节点的本地检测结果与融合中心检测结果的一致性越高其可信度越高。感知节点每一次感知过程中,根据融合中心的检测结果自动更新自己的可信度因子。
定义 设ui,m为第i个感知节点在m次检测时本地检频谱测结果与融合中心频谱检测结果相同的累积次数,uFC,m为融合中心FC进行全局频谱检测总次数,则第i个感知节点在第m次检测时的可信度因子定义为

显然,感知节点本地检测结果与融合中心检测结果一致的次数越大,可信度就越高。
2.2 协作节点选择
采用协作频谱检测虽然提高了检测概率,但是随着参与协作检测感知节点数目的增大,频谱检测的性能趋于平缓;相反,过多的感知节点参与协作检测会使整个无线电网络中的检测时间过长,也会造成巨大的系统开销。针对这一问题,利用切尾平均数法确定可信度门限来选取采可信度值大于门限值的用户参与协作检测。这样一方面提高了频谱检测性能,另一方面减少了参与协作的用户数,节省了系统的额外开销。
切尾平均数[15]是将一组数据中的其中一个最大值和最小值去掉后其余数值的平均数。切尾平均数法去掉了数列中影响数据稳定性的极端值,从而能具有较好的稳健性,不易受到极端因素的影响。在数据序列本身存在少量错误的情况下,通过有效的判定极端值,并将极端值去掉,可以获得较为真实的反应数据情况的平均指标。依据切尾平均数法,首先对感知节点i在第m次检测的可信度因子进行排序。不妨假设r1,m<r2,m<…<rM,m,则排序后的可信度向量为
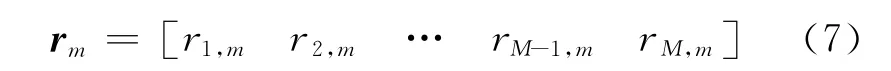
去掉可信度因子最大和最小的两个感知节点,得到可信度向量

对可信度向量r′m中的M-2个用户的可信度因子求平均值

将可信度因子高于该平均值(可信度门限)的K个感知节点参与协作,组成一个新的可信度向量
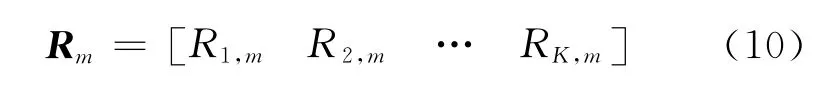
在融合中心,利用可信度因子计算参与协作的每个感知节点的加权系数,加权统计判决量。由此得到融合中心第m次频谱判决的统计量为
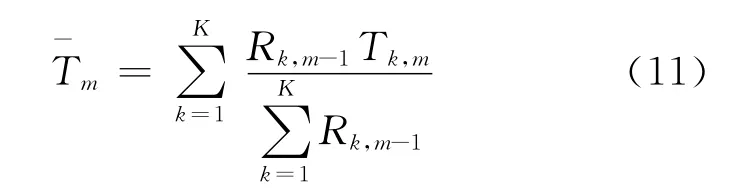
式中:Tk,m为第m次频谱检测时参与协作的第k个感知节点传递给融合中心的频谱检测统计量。
最后,根据式(5)的判决门限和式(4)的判决规则,融合中心做出全局判决。
2.3 算法实现
根据以上分析可得基于可信度的加权协作频谱检测算法的主要步骤为:
步骤1 初始化。每个感知节点的可信度初始值设为1。
步骤2 感知节点构建信号采样数据矩阵,计算得出采样协方差矩阵(N)。
步骤3 感知节点根据(N)计算其最大和最小特征值λmax和λmin,采用MMED检测获得本地检测信息,发送至融合中心。
步骤4 融合中心根据去尾平均法获得可信度门限值。选择可信度因子大于可信度门限的感知节点参与融合中心的协作检测。
步骤5 融合中心按照参与协作的各感知节点的可信度因子对其检测统计量加权,形成融合中心检测统计量。
步骤6 融合中心判决。将加权后的检测统计量与判决门限比较。当≥γ时,PU信号存在;反之,PU信号不存在。
步骤7 感知节点将各自的本地检测结果与融合中心的全局检测结果比较,更新其可信度因子,以供下一次频谱检测中使用。
步骤8 循环执行步骤2至步骤7。
WCSA算法的流程图如图2所示。

图2 WCSA算法流程图Fig.2 Flow chart of WCSA algorithm
3 仿真与分析
在高斯信道下对WCSA算法的频谱检测性能进行了仿真验证。为了便于比较,同时给出了在相同环境下的本地检测采用MMED算法下基于信噪比加权的协作频谱检测算法(Weighted based on maximum minimum eigenvalue detector,WSMME)算法和本地检测采用能量检测的信噪比加权协作频谱检测(Weighted based on SNR ener-gy detector,WSED)算法的性能仿真。在仿真中,假设认知无线电网络的频谱检测主信号为BPSK信号,数据传输速率为256kbits/s,载波频率为500MHz,系统的虚警概率为0.01,过采样因子L=16,感知节点数为M=16,每次仿真都是基于10 000次的蒙特卡罗计算。由于存在噪声不确定性,噪声方差的实际值在一定范围内波动,设ξ为噪声波动随机性参数,定义噪声波动随机性因子为U则真实的噪声方差在内取值。假设初始噪声方差
图3是信噪比(Signal to noise ratio,SNR)为-16dB的情况下,3种不同算法的频谱检测概率随采样点数变化的比较。图中 WSED-0dB,WSED-0.5dB,WSED-1dB分别表示噪声波动随机性因子为0,0.5,1dB时 WSED算法的频谱感知性能。从图3中可以看出随着采样点数的增加,3种算法的检测概率均有所提高。由于WCSA和WSMME算法的频谱检测判决量与信道噪声无关,因此这两种算法对噪声不确定性不敏感,其频谱检测性能与噪声不确定性无关,并且随着采样点数的增加而迅速增长;而WSED算法在噪声在存在噪声不确定性时其检测概率随着采样点数的增加而增长较为缓慢,噪声不确定性对其有较大的影响。
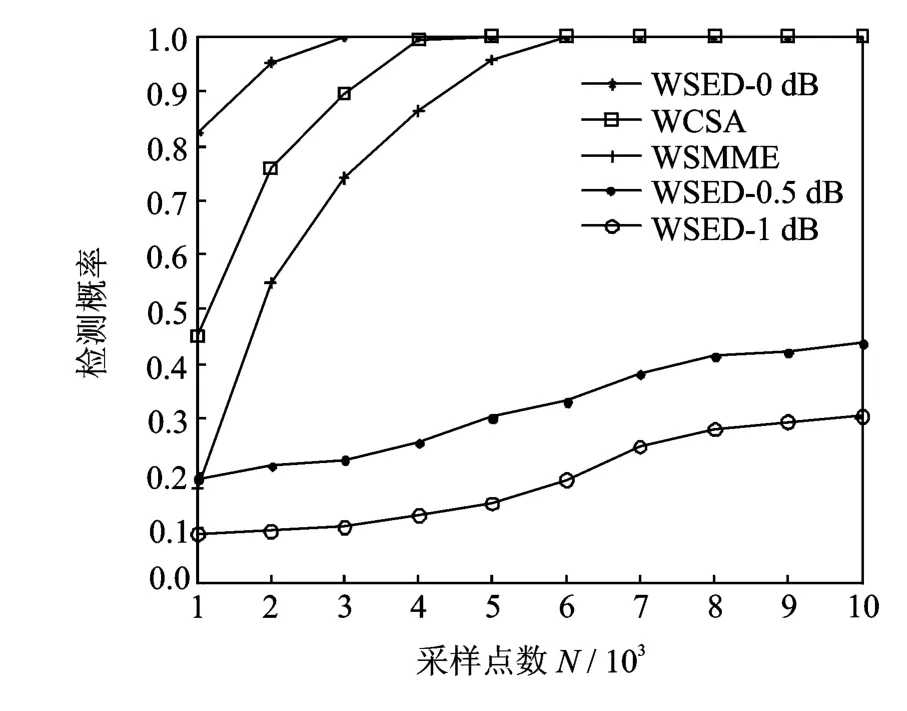
图3 不同算法的检测概率随采样次数变化曲线Fig.3 Detection probabilities of different algorithms as sampling number
图4和图5是采样点数为1 024的情况下,三种不同算法的检测概率和虚警概率性能随信噪比变化的情况。从仿真结果曲线可以看出,当噪声稳定时,WSED算法的检测性能是最优的。但是在噪声不确定性存在的情况下,WCSA算法的检测性能是最优的,WSMME的检测性能次之,WSED的检测性能却随着噪声波动性的增大而明显下降。特别需要指出的是WCSA算法和WSMME算法的虚警概率几乎接近于0。综合来说,在实际噪声波动的环境中WCSA算法是最优的。
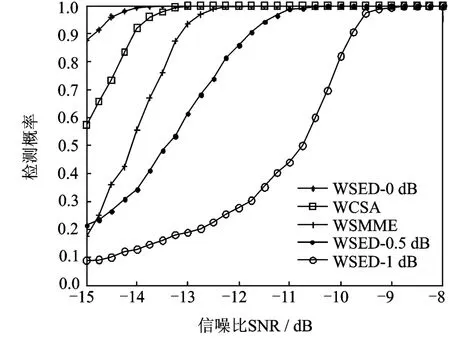
图4 不同算法的检测概率随信噪比变化曲线(N=1 024)Fig.4 Detection probabilities of different algorithms as SNR when N=1 024
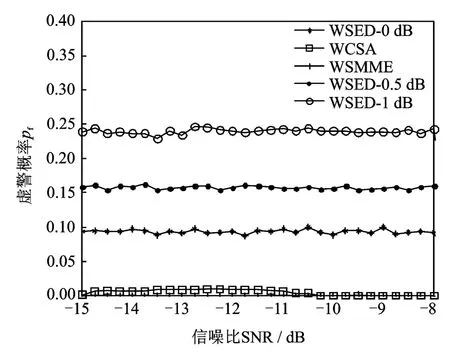
图5 不同算法的虚警概率随信噪比变化曲线图Fig.5 False alarm probabilities of different algorithms as SNR
图6是采样点数N=2 048时WCSA、WSMME和WSED三种不同算法的检测概率随信噪比变化的比较。可以看出3种算法的检测性能趋势与N=1 024时是一致的。
图7是采样点数为1 024的情况下,WCSA算法与其他几种加权算法的检测性能比较。从图中可以看出,随着信噪比的增加4种算法的检测概率均增加。当WCSA算法的SNR为-13.7dB时,其检测概率已接近为1;而对于检测概率加权、均值加权[9]和WSMME算法,如果要求检测概率接近1,则对应的SNR分别为-12.7,-11.0和-12.0dB。也就是说 WCSA算法的检测性能分别优于其他3种算法1,2.7和1.7dB左右。

图6 不同算法的检测概率随信噪比变化曲线(N=2 048)Fig.6 Detection probabilities of different algorithms as SNR when N=2 048

图7 基于MMED不同加权算法的检测概率随Fig.7 Detection probabilities of different algorithms based on MMED as SNR

图8 WCSA算法中参与协作的节点数的变信噪比变化曲线变化情况Fig.8 Number of participating cooperation nodes as total nodes
图8为信噪比-13dB时,WCSA算法参与协作检测的节点数随总节点数变化的情况。从图中看出,随着总节点的增加,参与协作的节点数基本呈线性增加。当M=16时,参与协作的平均节点数为9。也就是说WCSA算法参与协作的用户点数比无可信度门限设置全部节点参与协作时减少了43.75%,明显节省了系统的额外开销。
由此可见,提出的WCSA算法通过设置可信度门限减少参与协作的用户数,提高频谱检测性能,并保持了MMED算法检测性能不受噪声不确定影响的优点。
4 结束语
频谱感知对于实现认知无线电至关重要,如何高效地进行频谱感知是近期研究的一个热点。为了提高多用户下的协作频谱感知的检测性能,本文提出了基于可信度的最大特征值协作频谱检测算法。该算法在保证检测性能指标的前提下,减少参与协作的感知用户数,提高频谱检测性能,并且有效克服噪声不确定性。仿真结果表明,WCSA算法的频谱检测性能要优于其他算法1~3dB,系统开销节省43.75%左右。
[1]Mitola J,Maguire G Q.Cognitive radio:Making software radios more personal[J].IEEE Personal Communications,1999,6(4):13-18.
[2]Cabric D,Mubaraq S M,Brodersen R W.Implementation issues in spectrum sensing for cognitive radios[C]//Conference Record of the Thirty-eighth Asilomar Conference on Signals,Systems and Computers.Pacific Grove,California,USA:IEEE,2004:772-776.
[3]Mishra S M,Sahai A,Broderson R W.Cooperative sensing among cognitive radios[C]//IEEE International Conference on Communications.Istanbul,Turkey:IEEE,2006:1658-1663.
[4]Zeng Yonghong,Liang Yingchang.Maximum-minimum eigenvalue detection for cognitive radio [C]//IEEE 18th International Symposium on Personal,Indoor and Mobile Radio Communications.Athens:IEEE,2007:1-5.
[5]Zeng Yonghong,Liang Yingchang.Eigenvalue based spectrum sensing algorithms for cognitive radio[J].IEEE Transaction on Communications,2009,57(6):1784-1793.
[6]Penna F,Garello R,Spirito M.Cooperative spectrum sensing based on the limiting eigenvalue ratio distribution in wishart matrice[J].IEEE Communications Letters,2009,13(7):507-509.
[7]胡晓宁,胡捍英,仵国锋.认知无线电协作频谱感知机制的优化 [J].数据采集与处理,2011,26(6):691-696.Hu Xiaoning,Hu Hanying,Wu Guofeng.Optimization for cooperative spectrum sensing in cognitive radio networks[J].Journal of Data Acquisition and Processing,2011,26(6):691-696.
[8]王海军,粟欣,王京.认知无线电中的协作频谱检测技术 [J].中兴通讯技术,2009(4):10-14.Wang Haijun,Su Xin,Wang Jing.Cooperative spectrum detection techniques in cognitive radio[J].ZTE Technology Journal,2009(4):10-14.
[9]Ma Jun,Li Ye.Soft combination and detection for cooperative spectrum sensing in cognitive radio networks[C]//IEEE Global Telecommunications Conference.Washington:IEEE,2008:4502-4507.
[10]王春生,刘林.基于信噪比加权的合作频谱感知检测算法 [J].无线通信技术,2011(1):37-41.Wang Chunsheng,Liu Lin.Weighted cooperative spectrum sensing technology based signal noise ratio[J].Wireless Communication Technology,2011(1):37-41.
[11]Wang Chinliang,Chen Hanwei,Chou Yuren.A credibility-based cooperative spectrum sensing technique for cognitive radio systems[C]//2011IEEE 73rd Vehicular Technology Conference.Yokohama,Japan:IEEE,2011:1-5.
[12]Huang Xiaoge,Han Ning,Zhang Guanbo,et al.Weighted-collaborativee spectrum sensing in cognitive radio[C]//Second International Conference on Communications and Networking in China.Shanghai,China:IEEE,2007:110-114.
[13]Yang Wendong,Cai Yueming,Xu Youyun.A fuzzy collaborative spectrum sensing scheme in cognitive radio[C]//International Symposium on Intelligent Signal Processing and Communication Systems.Xiamen,China:IEEE,2007:566-569.
[14]Tulino A M,VerdúS.Random matrix theory and wireless communications[M].Hanover,USA:Now Publishers Inc,2004:19-95.
[15]龚曙明,朱海玲.应用统计学 [M].北京:中国水利水电出版社,2010:79-80.Gong Shuming,Zhu Hailing.Applied statistics[M].Beijing:China Waterpower Press,2010:79-80.

