刚性面加筋土挡墙工作性状与设计方法探讨
王协群,邹维列,冷建军,刘家国,邓卫东
(1.武汉大学岩土与结构工程安全湖北省重点实验室,武汉 430072;
2.武汉理工大学 土木工程与建筑学院,武汉 430070;3.Tenax Corporation,Baltimore MD 21205,USA;4.深圳地质勘察局,深圳 518015;5.招商局重庆交通科研设计院有限公司,重庆 400067)
1 研究背景
传统重力式挡墙是以墙体自身重量抵抗墙后填土的压力来维持稳定的。当挡墙高度较大时,作用在挡墙上的土压力也很大,使挡墙体型变得十分肥厚,很不经济。法国工程师Henri Vidal于1966年采用镀镍钢条作为加筋材料,成功修建了一座公路加筋土挡墙[1]。随后,加筋土挡墙技术在欧美、日本、中国等地得到了推广应用和发展,其间加筋材料也经历了一个从金属材料向土工合成材料发展的过程。在计算方法上,较多地采用传统的“极限平衡法”。这种方法简便实用,但无法评价筋材与土的应力、应变和挡墙结构的变形。因此,数值计算方法越来越多地被用于加筋土挡墙的工作性状分析[2-4]。可以说,目前国内外对普通加筋土挡墙的研究已经十分深入,成果也很丰富。
工程中采用的普通加筋土挡墙与传统的重力式挡墙是2种不同的挡土结构,且前者比后者的墙面厚度要薄得多,故也被称为“轻型挡墙”,特别是当挡墙较高时,经济效益更为显著。
但与重力式挡墙相比,通常用作加筋土挡墙墙面的混凝土面板或模块,仅起美观和防护作用,设计上并不承担(或仅考虑部分承担)墙后土压力,不仅制作和安装都较复杂,而且当墙顶面上有较大堆载作用时,侧向变形很大。故对变形有严格要求的工程,其应用会受到限制。因此,在实践中,我国工程技术人员又创造性地将重力式挡墙与加筋挡墙结合起来,即在重力式挡墙墙后填土中铺设土工格栅或土工织物(其中大多数是土工格栅),形成“重力式加筋土挡墙”[5-6],以发挥二者各自的优点,扬长避短;在日本,以龙冈文夫(F.,Tatsuoka)教授和本馆山胜博士为核心,提出了在日本铁路系统中已成为标准加筋挡墙技术的RRR(Reinforced Road with Rigid Facing Construction System)工法[7-8]。概括起来说,RRR 工法就是采用具有抗弯曲变形能力的钢筋混凝土墙面(Full-Height Rigid,简记为FHR)和加筋材料来构筑倾斜或垂直坡面的工程技术。这种挡墙被称为“全高刚性面加筋土挡墙”,其墙面厚度比我国已建重力式加筋土挡墙的墙体厚度更薄。本文把这2种新型挡土结构统称为“刚性墙面加筋土挡墙”。
刚性墙面加筋土挡墙与传统重力式挡墙的不同是明显的,而与面板式(或模块式)加筋挡墙的不同则在于这种挡墙能有效约束墙后填土的侧向变形,并且在设计上要求墙体承担墙后土压力。
然而,目前我国关于刚性墙面加筋挡墙的理论研究落后于实践,对其工作性状、设计理论与方法都缺少系统、深入的研究,相关规范也没有涉及。因此,面对实际工程,技术人员只能凭经验计算筋材拉力和墙背土压力[6],墙面厚度普遍比日本的FHR面要厚得多[5-6];在施工顺序上,我国既有采用“先填加筋土、后筑刚性墙”的,也有采用“先筑刚性墙、后填加筋土”的[6],显得较为盲目和随意。
本文采用数值分析方法,从筋材与填土的应力、应变和挡墙的变形等各个方面,评估上述2种不同施工顺序下,土工格栅加筋的重力式挡墙和全高刚性面挡墙的工作性状及土工格栅对挡墙性状的贡献。在此基础上,初步提出刚性墙面加筋土挡墙设计中,筋材拉力、墙后土压力等关键问题的确定方法。
2 数值分析的方法和模型
数值分析采用FLAC有限差分程序[9]。采用摩尔-库伦模型模拟土体材料;采用弹性模型模拟刚性挡墙;采用FLAC提供的接触面单元模拟接触面滑动或者拉开。接触面抗剪强度用摩尔-库伦准则Fmax=cL+Fntanφ。表达式中:c为沿接触面的黏聚力,L为有效接触长度,φ为接触面摩擦角,Fn为接触面上的法向作用力;土工格栅采用FLAC提供的索单元(Cable单元)模拟。使用索单元不需要另外设置筋土接触面,只需定义索单元和周围岩土的接触面参数,如接触面法向和切向刚度,接触面的黏聚力和摩擦角。
3 典型算例及分析
3.1 典型算例
数值分析针对墙顶有堆载的路堤式挡墙,计算模拟2种不同的施工顺序,一种是:①先浇筑完成刚性挡墙;② 填筑格栅加筋土;③堆填墙顶路堤土。以下将这种施工顺序记为“工序A”;另一种工序参考日本RRR工法的施工过程[7]:① 浇筑完成墙基(参见图1);②填筑完成格栅加筋土(墙后有格宾);③浇筑完成刚性挡墙;④堆填墙顶路堤土。以下将这种施工顺序记为“工序B”。工序A的刚性墙假设为重力式混凝土挡墙,工序B的刚性墙假设为FHR面混凝土挡墙。
3.1.1 计算模型的几何参数和边界条件
如图1(a)所示,重力式加筋挡墙的墙高为12m,墙顶宽度为1m,墙底宽度为3 m。挡墙建于地基土之上,入土深度为2m(即地面以上挡墙高10m)。墙后填土厚度为10m;墙顶以上有8 m路堤土(填土坡度为1∶1.5)。这里路堤填土采用作用于墙顶的堆载模拟(挡墙后12m范围呈三角形分布,此后为160kPa的均布荷载)。挡墙后填土内共铺设19层土工格栅,长度为9 m,竖向间距为0.5m。格栅与挡墙之间没有连接。
如图1(b)所示,FHR面加筋土挡墙的墙高为10m,墙体厚度为1m,墙体倾角为84.3°(水平和竖向比为1∶10)。墙基厚1m,宽2m,建于地基土之上,入土深度为1.0m。墙后填土厚度为10m,挡墙和墙后填土之间设置1m宽的格宾。其余同重力式加筋挡墙。
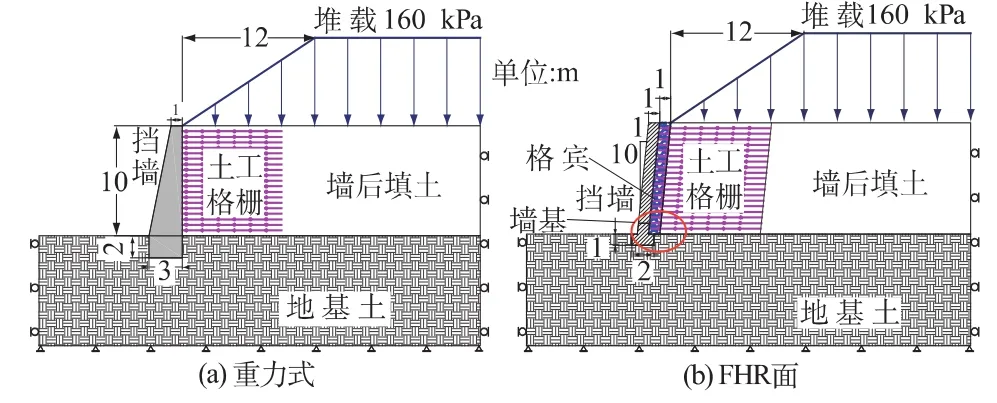
图1 加筋土挡墙典型算例的计算模型Fig.1 Calculation model for geosynthetic-reinforced soil retaining wall(GRSRW)
3.1.2 材料与接触面参数
在这2个典型算例中,地基土、墙后填土、格宾和挡墙的模型参数见表1。填土与地基土、挡墙与地基土、挡墙与填土或格宾3个接触面的抗剪强度参数见表2。选用的土工格栅厚度为2.5mm,抗拉强度为50 kN/m,抗拉刚度为500 kN/m,其它参数(包括格栅与填土的接触面强度参数)见表3。

表1 地基土、墙后填土、格宾和挡墙的材料模型与参数Table 1 Models and parameters for foundation soil,filling soil behind the wall,gabion and retaining wall
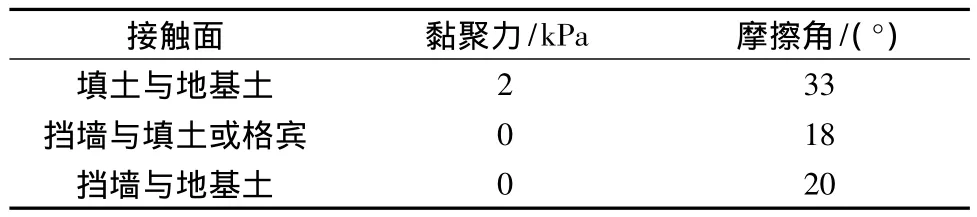
表2 接触面的抗剪强度参数Table 2 Strength parameters of contact faces

表3 土工格栅和索单元参数Table 3 Parameters of geogrid and cable element
需要说明的是,以上参数取值充分考虑了这些材料特性的一般状况,但并非来自实测结果。
3.2 计算结果与分析
用FLAC数值计算可以获得挡墙、地基土和填土的位移与应力场(限于篇幅,本文没有给出)、土工格栅的拉力及拉应变。以下分墙后填土到墙顶和墙顶堆载完成后2个阶段的数值计算结果进行分析。
3.2.1 水平位移
3.2.1.1 工序 A
从图2可以看出,重力式加筋土挡墙的水平位移沿墙高呈线性分布,墙顶处最大。
挡墙水平位移的产生有墙体平移和绕墙底转动2种模式。挡墙的平移受土工格栅的影响很小,墙底处水平位移约为6.5mm(墙后填土到墙顶)和12mm(墙顶堆载完成后)。墙后填土到墙顶时,墙顶处最大水平位移为25.6mm(不铺土工格栅)和22.6mm(铺土工格栅);墙顶堆载完成后,挡墙水平位有显著增加,墙顶处最大水平位移为108mm(不铺土工格栅)和54.4mm(铺土工格栅)。可见采用土工格栅加筋可以减小挡墙和墙后填土的水平位移(对于重力式挡墙而言主要是绕墙底转动产生的水平位移)。土工格栅的这种贡献与挡墙和墙后填土水平位移的大小有关:从上述结果可知,填土到墙顶时,挡墙和墙后填土水平位移相对较小,土工格栅对减少水平位移的作用较小(墙顶处最大位移大约减小16%);在墙顶堆载完成后,挡墙和墙后土体水平位移增大的同时,土工格栅减少水平位移的作用也更加明显(墙顶处最大水平位移大约减小50%)。
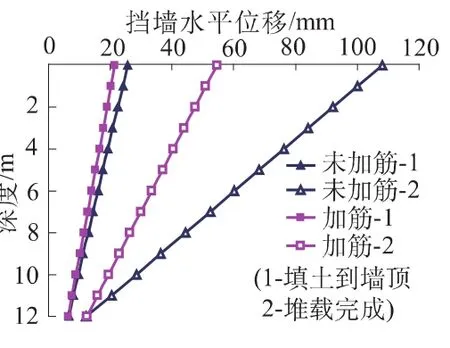
图2 重力挡墙水平位移Fig.2 Lateral displacement of gravity wall facing
3.2.1.2 工序 B
从图3可见,FHR墙面的水平位移沿墙高仍然呈线性分布,在墙顶处最大;在同一高度,格宾的水平位移最大;沿深度方向,从深度2.0m到5.0m范围内水平位移最大(可形象地称之为“鼓肚子”现象,这在普通加筋土挡墙中比较常见);从深度5.0m到挡墙底部,水平位移大致呈线性减小。
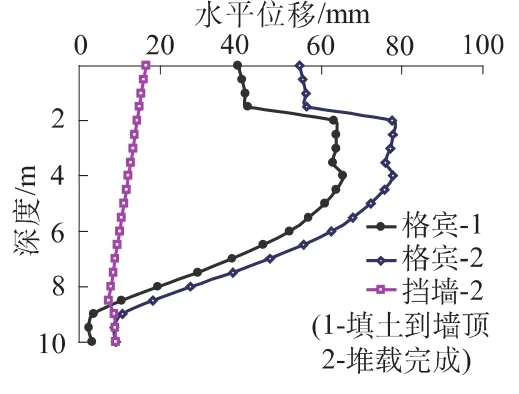
图3 FHR面挡墙和格宾水平位移Fig.3 Lateral displacements of full-height rigid facing and gabion
墙后填土到墙顶时,格宾最大水平位移为65.3mm(深 度 为4.0m处);堆载完成后格宾和墙后填土的水平位移增加,其中格宾的最大水平位移为77.7mm(深度为4.0m处)。可见,墙后填土至墙顶时,格宾的水平变形已经达到堆载完成后其总水平变形的84%。换言之,对于工序B,由于FHR面挡墙的主体部分(d=0~9.0m,d为墙顶以下的深度)是在填土到墙顶以后、墙顶堆载之前浇注的,因此墙顶堆载完成后引起挡墙最大水平位移(位于挡墙顶部)仅为16.6mm(见图3),与工序 A(54.4mm)相比,工序B的挡墙水平位移明显要小得多。
加筋土挡墙需满足承载力极限状态和正常使用极限状态两方面的要求,即在防止挡墙失稳的同时也要防止变形过大。因此工序B更能满足防止挡墙和填土变形过大的要求。
3.2.2 水平应力
3.2.2.1 工序 A
从图4(a)可见,墙后水平土压力总体趋势随深度而线性增加,但在填土底部附近呈非线性降低(这是由于填土与地基土分界面的摩阻作用所致),与库伦主动土压力的水平分力(为比较方便,称其为“理论解”,下同)沿深度为线性分布并不相同;从墙后填土至墙顶再到堆载完成,墙后填土压力有明显的增大。
数值分析结果表明:填土到墙顶后,不考虑加筋时挡墙水平土压力为234.1 kN/m,考虑加筋时为224.5 kN/m;墙顶堆载完成以后,不考虑加筋时挡墙水平土压力为351.1 kN/m,考虑加筋时为325.7 kN/m。
这说明采用工序A,尽管加筋可以减小挡墙土压力,但填土至墙顶时,加筋仅减小水平土压力约4.1%,堆载完成以后,加筋也只减小了7.2%,没有发挥出格栅加筋的作用。
3.2.2.2 工序 B
从图4(b)可知,格宾后填土的水平土压力沿深度基本上为非线性分布,与库伦主动土压力水平分力的线性分布规律差别很大。从墙后填土至墙顶再到堆载完成,格宾后填土水平土压力有明显的增大。
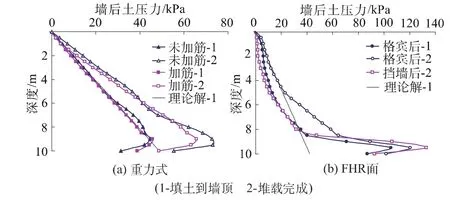
图4 加筋土挡墙水平土压力分布Fig.4 Distribution of lateral soil pressure on GRS RW
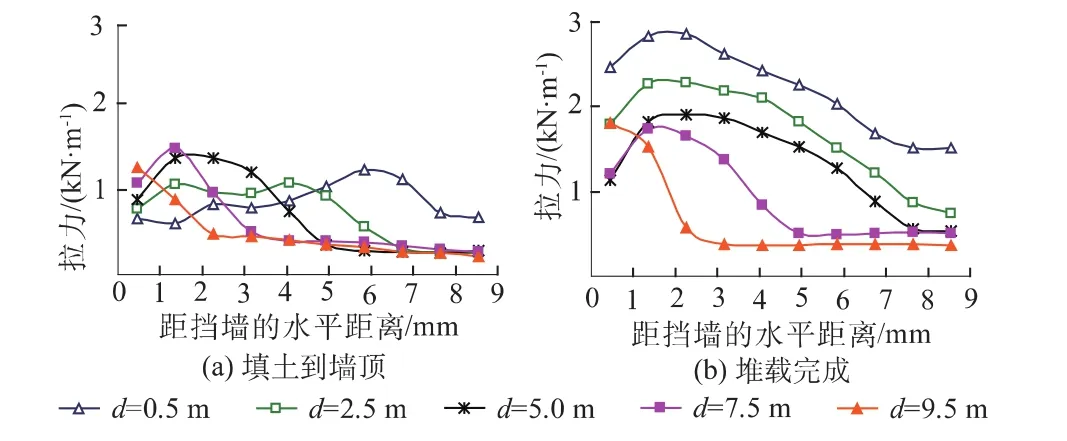
图5 重力式加筋土挡墙中土工格栅拉力沿长度方向的变化Fig.5 Variation of tension along geogrid length in GRS RW with a gravity wall facing
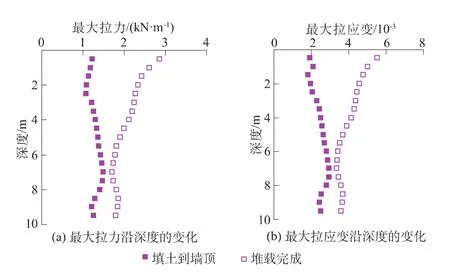
图6 重力式加筋土挡墙中土工格栅最大拉力和最大拉应变沿深度的变化Fig.6 Variations of maximum tension and maximum strain in geogrid along depth in GRS RW with a gravity wall facing
在工序B下,水平土压力分布表现出与工序A很大的不同:填土至墙顶时(此时FHR面挡墙尚未浇筑),能充分发挥土工格栅的加筋作用。因此在填土的上部和中部区域(d=0~8.0m),格宾后填土水平土压力增加比较缓慢,比库伦土压力明显要小。但在接近填土底部的区域(d=8.0~10.0m),水平土压力增幅很大,特别是在d=9.0~10.0m区域,由于受墙基(填加筋土前已先行浇筑完成,见图1(b))底面、墙后填土底面与地基土的界面摩阻所产生的侧向约束作用比较明显,其水平土压力达到或超过了静止土压力。
由于FHR面挡墙主体是填加筋土到墙顶以后、墙顶堆载之前浇注完成的,因此在墙顶堆载完成以后,堆载引起加筋填土的继续变形受到了刚性挡墙的抑制,而格栅拉力与其变形相关,从下一节“土工格栅张拉力和拉应变”的分析可知,此时格栅承担由堆载引起的水平土压力增量不大,所以拉应变增量也不大,堆载引起的水平土压力主要由FHR面挡墙承担了。但堆载完成以后,挡墙主体的墙后水平土压力较格宾后填土水平压力明显要低,见图4(b)。
数值分析结果表明,填土到墙顶时,挡墙主体(d=0~9 m)水平土压力总和为163.6 kN/m;堆载完成以后为267.0 kN/m。
对比工序A和工序B在不同施工阶段时挡墙墙后土压力的的计算结果可知,工序B的墙后土压力比工序A小得多。
3.2.3 土工格栅的张拉力及拉应变
3.2.3.1 工序A
图5和图6分别为重力式加筋土挡墙墙后填土到墙顶和堆载完成后,土工格栅拉力沿格栅长度方向的变化和土工格栅最大拉力沿深度方向的变化。
沿长度方向,各层土工格栅中拉力的分布不均匀,最小拉力一般在距离挡墙最远的位置,而最大拉力可能是在最靠近挡墙的位置或者是更远的某一位置。随着挡墙承受荷载的增加(从填土至墙顶再到堆载完成),各层格栅中最大拉力的位置朝挡墙方向靠拢(见图5)。
沿深度方向,由于格栅与重力挡墙之间没有连接,二者是通过变形协调传递压力的,因此,当堆载完成使格栅比填土至墙顶时产生更大变形以后,各层格栅的最大拉应变沿深度的变化(见图6)与重力挡墙沿深度的水平变形(见图2)大致是一致的。
填土到墙顶时,各层格栅中最大拉力的最大值为1.5 kN/m(仅为其抗拉强度50 kN/m的3%),最大拉应变仅为0.29%,出现在偏下部(d=7.0m)的位置;墙顶堆载完成后,格栅拉力有明显增加,但格栅中最大拉力的最大值也仅为2.9 kN/m(为其抗拉强度的6%),最大应变仅为0.55%,出现在深度最小(d=0.5m)的位置。由此可见,采用工序A,格栅中的拉应变很低,最大拉力也远低于其抗拉强度。
3.2.3.2 工序 B
由于与工序A的施工工序不同,沿长度方向,尽管各层土工格栅中拉力的分布也是不均匀的,但从填土至墙顶再到堆载完成,拉力分布的变化很小,各层格栅中最大拉力的位置并不朝挡墙方向靠拢(见图7)。
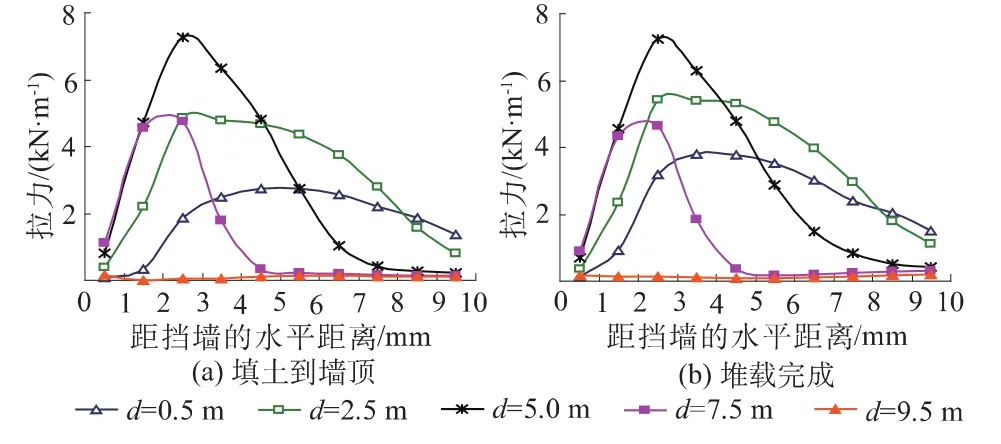
图7 FHR面加筋土挡墙中土工格栅拉力沿长度方向的变化Fig.7 Variation of tension along geogrid length in GRS RW with a full-height rigid facing
沿深度方向,从填土至墙顶再到堆载完成,填土中部以上区域格栅的拉力和拉应变增加,其中接近填土顶部处(d=0~2.0m)的增加尤为明显,而填土中部以下区域土工格栅的拉力和拉应变基本上没有增加。
无论是填土至墙顶还是堆载完成以后,各层土工格栅中的最大拉力和最大拉应变沿深度变化的峰值都出现在沿深度的中部,接近底部最低(见图8)。
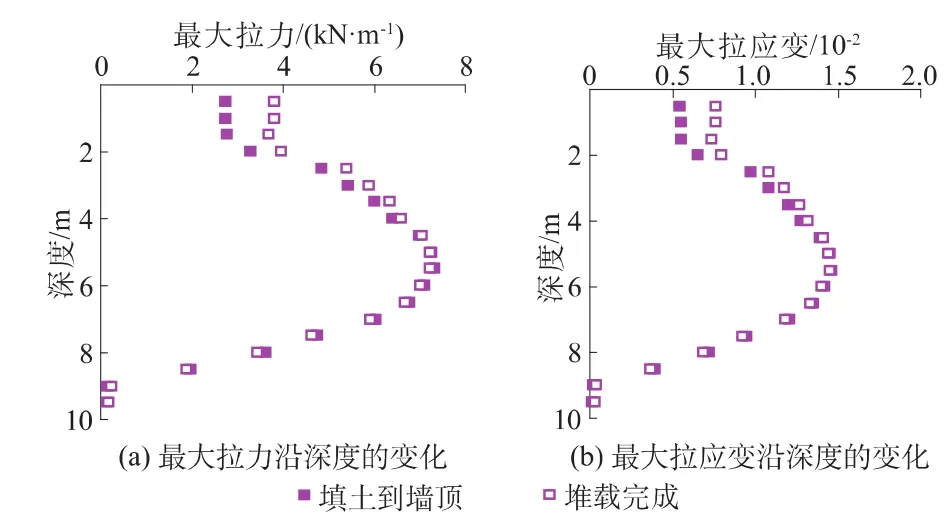
图8 FHR面加筋土挡墙中土工格栅最大拉力和最大拉应变沿深度的变化Fig.8 Variation of maximum tension and maximum strain in geogrid along depth of GRS RW with a full-height rigid facing
这一分布规律与AASHTO[10-11]假定的沿深度为线性分布、FHWA[12]假定的沿深度为均匀分布有很大的不同。填土到墙顶时,最大拉力峰值为7.31 kN/m(为其抗拉强度的14.6%),最大拉应变峰值为1.46%;墙顶堆载完成后,最大拉力峰值为7.25 kN/m(为其抗拉强度的14.5%),最大拉应变峰值为1.45%,与填土至墙顶时相比,有一定变化,但变化很小。很明显,这与填土至墙顶以后、墙顶堆载之前浇筑了刚性挡墙有关,即刚性挡墙的约束使墙顶堆载引起格栅的拉应变增量不大。
综上所述,与工序A比较,采用工序B有如下优点:
(1)土工格栅的最大拉应变和最大拉应力更大,能有效发挥其加筋作用。土工格栅中较大的拉应变和拉力能维持填土和格宾的稳定,有效降低墙后填土对刚性墙面的土压力。因此采用工序B的刚性墙面厚度可以比工序A的重力式挡墙的厚度薄得多。
(2)能有效控制墙顶堆载后填土和挡墙的水平变形。挡墙水平位移控制是挡墙设计中需要考虑的一个重要方面。因此,先用格宾和土工格栅进行填土、后浇筑刚性墙面的工序B在这一点上明显优于工序A。
(3)工序B在填土和挡墙中间有格宾,可以有效改善挡墙墙后排水条件,对维持挡墙的长期稳定有积极作用。
因此,在以下对刚性墙面加筋土挡墙的分析中,只针对工序B进行论述。
需要指出的是,以上比较2个采用不同工序的刚性墙面加筋土挡墙算例,虽然在墙高、堆载、地基土和填土性质、加筋材料与加筋间距等主要参数上是相同的,但是也存在不同之处。比如挡墙断面、挡墙倾角以及是否包括格宾等。但这些差别不会对结果产生根本性的影响。
4 刚性墙面加筋土挡墙的筋材拉力和墙后土压力确定
刚性墙面加筋土挡墙设计的主要内容与普通加筋土挡墙基本上是相同的,都必须使之满足外部稳定性和内部稳定性的要求。不同之处在于还需要对承担土压力的刚性墙面进行专门的配筋计算,使之满足抗弯、抗剪的要求(本文对此不予讨论)。但采用刚性墙面加筋土挡墙的目的是通过充分发挥刚性挡墙和加筋土挡墙各自的优点,以有效控制填土和挡墙变形、减小墙后土压力。从前面对数值计算结果的分析可知,刚性墙面加筋土挡墙与普通加筋土挡墙的工作性状有以下不同之处,因此,如何正确计算其筋材拉力和墙后土压力是内部稳定性分析的关键。以下分别对两者进行详细分析。
(1)刚性墙面的格栅加筋土挡墙,墙体的水平位移从挡墙底沿墙高呈线性增加(见图2、图3)。而根据图9[13],结合墙后土压力与变形的关系可知,普通面板式格栅加筋挡墙的水平位移从挡墙底沿墙高的变化是非线性的。实际上,这从图3中FHR面挡墙浇筑之前,格宾后填土沿深度的水平位移分布也可以看出来。
(2)刚性墙面加筋土挡墙的墙后土压力由刚性墙面和加筋材料共同承担。
以上2点不同导致刚性墙面加筋土挡墙的墙后土压力计算不能简单地沿用普通面板式加筋土挡墙土压力的计算方法(见图9)。这种方法假定土压力是已知的,土压力的计算结果比实测结果大[14]。
对于刚性墙面加筋土挡墙,此方法无法考虑筋材拉力引起的墙后土体与挡墙之间作用力的降低,也必将导致土压力计算结果比实际值高,使得加筋材料的作用在极限平衡分析计算中无法体现。
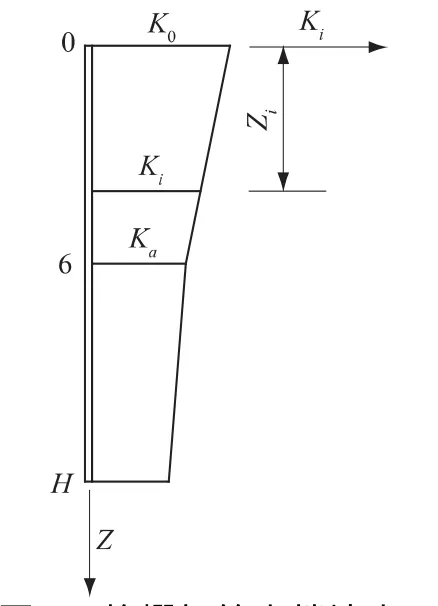
图9 格栅加筋土挡墙土压力系数分布[13]Fig.9 Distribution of soil pressure coefficient for geogrid-reinforced soil retaining wall[13]
4.1 筋材拉力的计算
目前在北美流行的美国AASHTO简化方法[10-11]不考虑墙面刚度、墙趾约束(主要是墙面自重产生的沿墙底的摩阻力)等因素对筋材拉力的影响,假定侧向土压力全部由筋材承担,并按下面(1)式验算各层筋材的拉力Ti,且要求各层筋材中的最大拉力满足下面(2)式的要求。
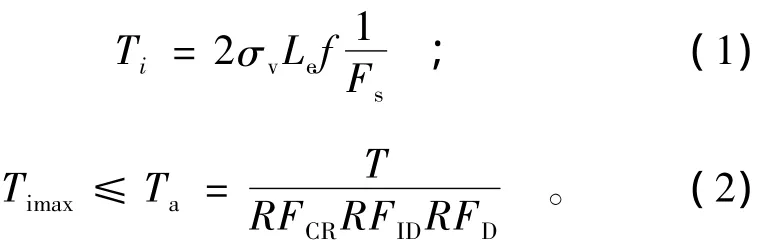
式中:Ti为第i层筋材的水平拉力(kN/m);σv为第i层筋材处的竖向压力(kPa);Le为筋材有效长度,即超出填土破裂面的筋材锚固段长度(m);F为筋材与周围土的摩擦因数;Fs为安全系数;Timax为各层筋材最大水平拉力中的最大值(kN/m);Ta为筋材的允许抗拉强度(kN/m);T为筋材的极限抗拉强度(kN/m);RFCR,RFID,RFD分别为筋材的蠕变折减系数、施工损伤折减系数和老化折减系数。
Bathurst等(2005)[13]认为AASHTO 方法对加筋土挡墙长期运行所需要的筋材拉力估计得过于保守;同样,Leshchinsky 等(2010)[15]、Han 等(2006)[16]也认为,如果考虑墙面的影响,AASHTO 方法[10-11]所给出的筋材拉力可能是保守的。但需要注意的是,Leshchinsky 等 (2010)[17]同时指出,按 Bathurst等(2005)[17]基于现场实测数据的回归分析所提出的呈“分段线性”分布的筋材拉力(见图10。图中H为墙高,z为筋材距墙底的位置高度)所得到的各层筋材最大拉力的合力ΣTmaxi可能不满足整体极限平衡的要求,导致筋材拉力被严重低估。
综上可见,对于刚性面加筋土挡墙,不言而喻,其筋材拉力比普通加筋土挡墙的筋材拉力要小。但到底该如何合理地计算?尽管可采用数值计算方法较为准确地确定,但目前尚无大家能接受的解析方法。因此建议仍采用式(1)、式(2)确定筋材拉力,以便于与目前国内通用的规范接轨。
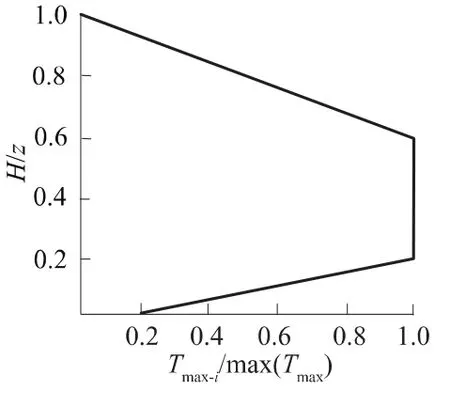
图10 由应变测值推算的归一化筋材拉力与归一化深度关系[15]Fig.10 Normalized reinforcement loads estimated from strain measurements as a function of normalized depth below wall top[15]
4.2 墙后土压力的确定
前述数值分析结果表明,刚性面加筋土挡墙墙后水平土压力较格宾后填土水平压力明显要低,且沿墙高呈明显的非线性分布,难以得到该分布的数学规律。为此,借鉴日本《RRR-B工法设计·施工规范》[18]中所提出的进行内部稳定性分析时所采用的“双楔法”来确定墙后土压力。
日本《RRR-B工法设计与施工规范》给出的“双楔法”(见图11)与德国建筑研究所(DIBT)对普通加筋土挡墙内部稳定性计算中采用的“双楔法”[19]本质上是相似的,只不过考虑到FHR墙面刚性大,因而滑动面仅限于通过墙踵的情况。此法是将图11中土楔F的下端a固定于挡墙墙踵,改变b的位置(通过改变θf和θb来实现)来寻找最小安全系数。
日本“双楔法”的具体步骤是(已经程序化):
(1)假定θf和θb得到某一个潜在滑裂面后,不计筋材的拉力,根据作用于2个土楔(见图11(b)中的F,B。图中Hf和Hb分别为土楔F和B的水平地震荷载)在各种荷载作用下力的极限平衡条件,即利用2个土楔力多边形的几何关系(见图11(c)),求得作用于挡墙墙后的土压力Pf。
(2)取包括墙体、土楔F,B在内的脱离体(见11(a)。图中Wgh为挡墙的水平地震力;Wgvtanφd为挡墙和地基之间的摩阻力。但在实际计算时,由于挡墙与地基之间的摩阻力并不明确,多数情况下不考虑(偏于安全),计入潜在破裂面ab,bc上作用的筋材拉力(各层筋材的拉力Ti按照(1)式计算),计算挡墙抗滑动稳定安全系数Fs和抗倾覆稳定安全系数Fo,直至所有潜在滑裂面中的最小安全系数Fsmin,Fomin均满足要求时,相应的土压力即为墙后土压力。如果Fsmin,Fomin中任意一个不满足规定要求,则通过改变筋材的布置(间距、长度)、或者采用抗拉强度更高的筋材等措施,按同样的方法重复计算,直至满足规定的安全系数为止。
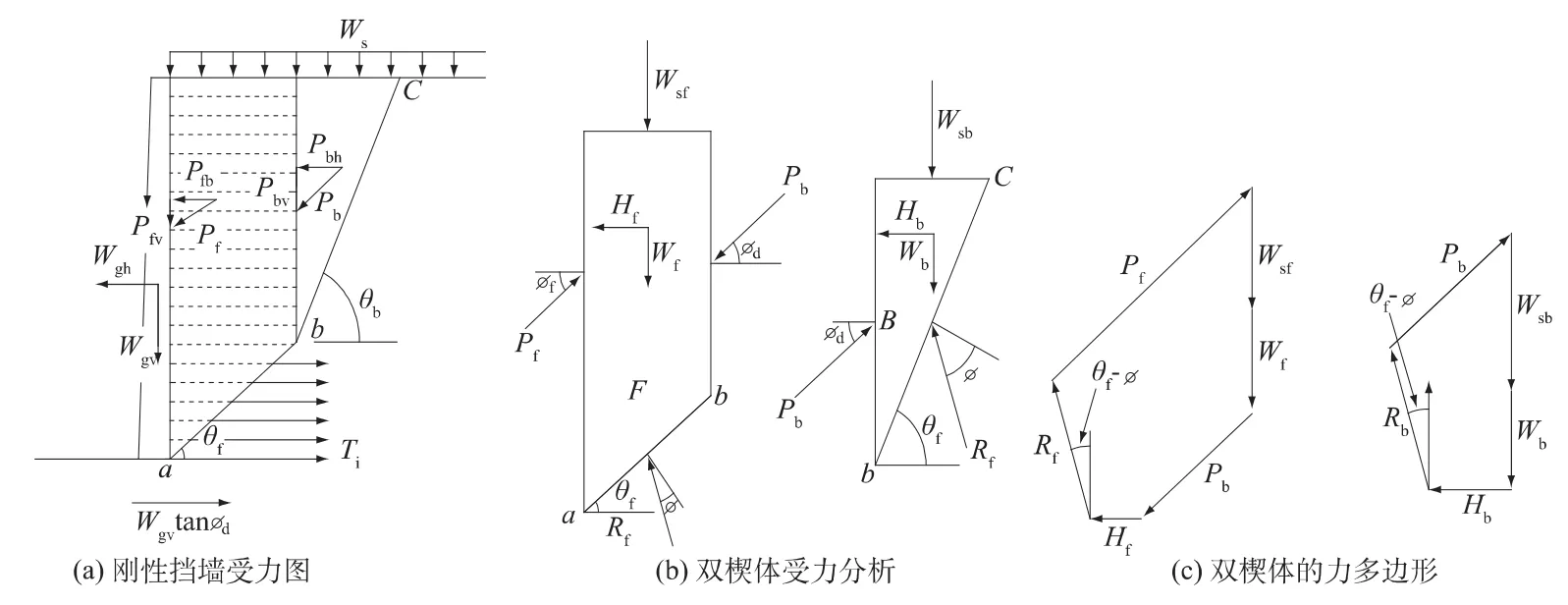
图11 日本“双楔体法”确定土压力方法示意图[18]Fig.11 Schematic diagram of the determination of soil pressure by two-part wedge method in Japan[18]
5 结论与建议
本文以墙顶有堆载填土的路堤挡墙为对象,通过数值分析手段,模拟2种不同施工顺序(文中分别称为“工序A”和“工序B”),分填土至墙顶和堆载完成后2个阶段进行计算分析,基本掌握了刚性墙面加筋土挡墙的工作性状。研究结果表明:
(1)刚性墙面加筋土墙体的水平位移分布与普通加筋土挡墙不同,从墙底沿墙高为线性分布,墙顶处最大。
(2)FHR面加筋土挡墙的墙背水平土压力比格宾后填土水平土压力明显要小,沿深度呈明显的非线性分布;筋材最大拉力和最大拉应变峰值都出现在沿挡墙深度的中部,接近底部最低。这一分布规律与AASHTO假定的沿深度为线性分布、FHWA假定的沿深度为均匀分布有很大的不同。
(3)工序A和工序B数值计算结果的对比分析,表明采用工序B的FHR面加筋土挡墙有更明显的优势,可有效发挥格栅的加筋作用,减小墙后土压力,约束墙体的侧向变形,建议在实际工程中采用。
(4)探讨了刚性墙面加筋土挡墙的设计方法。由于采用工序B的FHR面加筋土挡墙承担部分土压力,其格栅拉应力比普通加筋土挡墙的格栅拉应力要低。但鉴于目前还难以提出其合理的解析计算方法,因此建议采用式(1)和式(2)计算;而墙后土压力建议借鉴日本《RRR-B工法设计与施工规范》给出“双楔法”计算。
[1]VIDAL H.The Principle of Reinforced Earth[J].Highway Research Record,1969,282:1-16.
[2]马玉静,魏然.土工格栅加筋土挡墙工作性能参数的有限元分析[J].国防交通工程与技术,2009,(1):25-28.(MA Yu-jing,WEI Ran.An Analysis of the Performance Parameters of Geogrids-reinforced Earth Retaining Walls with the Finite Element Method[J].Traffic Engineering and Technology for National Defense,2009,(1):25-28.(in Chinese))
[3]ROWE R K,SKINNER G D.Numerical Analysis of Geosynthetic Reinforced Retaining Wall Constructed on a Layered Soil Foundation[J].Geotextiles and Geomembranes,2001,19(7):387-412.
[4]栾茂田,李敬峰,肖成志,等.土工格栅加筋挡墙工作性能的非线性有限元数值分析[J].岩石力学与工程学报,2005,24(14):2428-2433.(LUAN Mao-tian,LI Jing-feng,XIAO Cheng-zhi,etal.Numerical Analysis of Performance of Geogrids-reinforced Retaining Walls by Nonlinear FEM[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(14):2428-2433.(in Chinese))
[5]邓昌中.加筋土路基力学行为的研究[D].重庆:重庆交通大学,2007.(DENG Chang-zhong.Study on Mechanical Behavior of Reinforced Subgrade[D].Chongqing:Chongqing Communication University,2007.(in Chinese))
[6]甘宜山.加筋土技术在重力式挡墙设计中的应用[J].基建优化,2003,24(2):42-43.(GAN Yi-shan.Application of Reinforced Earth Technique on Gravity Retaining Wall[J].Optimization of Capital Construction,2003,24(2):42-43.(in Chinese))
[7]TATSUOKA F,TATEYAMA M,UCHIMURA T,etal.Geosynthetic-Reinforced Soil Retaining Walls as Important Permanent Structures[J].Geosynthetics International,1997,4(2):81-136.
[8]TATSUOKA F,TATEYAMA M,MOHRI Y,etal.Remedial Treatment of Soil Structures Using Geosynthetic-reinforcing Technology[J].Geotextiles and Geomembranes,2007,25(4/5):256-265.
[9]Itasca.FLAC2D:Fast Lagrangian Analysis of Continua.Version 5.0[K].Minneapolis:Itasca Consulting Group Inc.,2005.
[10]AASHTO.Standard Specifications for Highway Bridges[M].Washington,D.C:AASHTO,1999.
[11]AASHTO.LRFD Bridge Design Specifications[M].Washington,D.C:AASHTO,2007.
[12]ELIASV,CHRISTOPHERB R,BERGR R.Mechanically Stabilized Earth Walls and Reinforced Soil Slopes Design and Construction Guidelines:Report No.FHWANHI-00-043[R].Washington D.C:Federal Highway Administration,2001.
[13]BATHURST R J,ALLEN T M,WALTERS D L.Reinforcement Loads in Geosynthetic Walls and the Case for a New Working Stress Design Method[J].Geotextiles and Geomembranes,2005,23(4):287-322.
[14]王 钊.土工合成材料[M].北京:机械工业出版社,2005.(WANG Zhao.Geosynthetics[M].Beijing:China Machine Press,2005.(in Chinese))
[15]LESHCHINSKY D,ZHUF,MEEHANCL.Required Unfactored Strength of Geosynthetic in Reinforced Earth Structures[J].Journal of Geotechnical and Geoenvironmental Engineering,2010,136(2):281-289.
[16]HANJ,LESHCHINSKY D.General Analytical Framework for Design of Flexible Reinforced Earth Structures[J].Journal of Geotechnical and Geoenvironmental Engineering,2006,132(11):1427-1435.
[17]杨广庆,周亦涛,周乔勇,等.土工格栅加筋土挡墙试验研究[J],岩土力学,2009,30(1):206-210.(YANG Guang-qing,ZHOU Yi-tao,ZHOU Qiao-yong,etal.Experimental Research on Geogrid Reinforced Earth Retaining Wall[J].Rock and Soil Mechanics,2009,30(1):206-210.(in Chinese))
[18]日本RRR工法协会.RRR-B工法设计与施工规范[S].2005.(Japan Association of RRR Construction Method.Japanese Code of Design and Construction for RRR-B Construction System[S].2005.(in Japanese))
[19]王 钊.国外土工合成材料应用研究[M].香港:现代知识出版社,2002.(WANG Zhao.Application of Geosynthetic Materials Abroad[M].Hong Kong:Modern Knowledge Press,2002.(in Chinese))

