球形储罐的抗震性能分析研究

郭龙玮，张大勇，2，杨智荣，王国栋，于哲敏，杨白冰

(1.大连海洋大学海洋与土木工程学院，辽宁大连 116023;2.大连理工大学海洋科学与技术学院，辽宁盘锦 124221;3.中国特种设备检测研究院，北京 100013)

0 引言

我国是个地震区分布较广的国家，辽宁海城地区(1975年)、唐山地区(1976年)、汶川地区(2008年)、玉树地区(2010年)等数起强烈地震，使人们生命财产遭受到严重损失。球形储罐广泛应用于石油、化工、冶金等部门，它可以用来作为液化石油气、液化天然气、液氧、液氨、液氮及其他介质的储存容器，也可作为压缩气体(空气、氧气、氮气、城市煤气)的储罐。由于它多用于储存易燃、易爆的物料，储量又大，如何防止它在地震中不发生严重损坏及引起危及人身和生产的灾害，成为目前社会研究的热点课题［1－3］。

球罐作为涉及生命安全、危险性较大的一种特种设备，在设计及评价标准中对地震的考虑仍然采用拟静力的处理方式，只给出球罐各部分强度的简化计算及校核方法［4－5］。现有的球罐设计规范可以保证结构在自重、内压及风载作用下的安全运行;而地震荷载作为球罐结构的主要控制荷载，对现役球罐造成了巨大的安全隐患，发生了很多事故［6－9］。国内外学者对球罐结构的抗震分析做了大量研究［2，10－13］，将荷载集中在球体中心，且支撑体系考虑为弹性结构，有关抗震设计规范［4］中将球罐简化为单自由度体系。利用附加质量法，忽略球罐内部液体晃动对支撑结构刚度的影响。

文中基于 ANSYS有限元软件，首先，建立2000 m3球罐力学模型，通过地震波激励下精确的时程反应分析，确定应力显著发生的位置;其次，分析该类球罐支撑结构设计参数(支柱数目、直径、壁厚、拉杆直径等)对球罐抗震性能的影响;最后，选取几种大、中、小型球罐，明确各类球罐的抗震性能。文中研究为球罐抗震安全保障及设计提供合理依据。

1 球罐有限元模型及地震波选取

1.1 球罐有限元模型

选取2000 m3的球罐为例，选用Shell 93单元模拟罐壁及各连板、支柱，Link 8单元模拟支撑拉杆。基于ANSYS软件，建立的有限元模型如图1所示。其中，球壳和连接板材料的密度7.83×103kg/m3，弹性模量 2.094 × 1011N/m2，泊松比0.262。球壳的直径15.7 m，壁厚44 mm，地面到球壳的中心距离为10.34 m。球罐由10根支柱支承，选用φ560 mm×10 mm钢管。在相邻支柱间设有交叉的拉杆，截面直径50 mm，10对，以增强稳定性。其他板及杆件的材料密度7.83×103kg/m3，弹性模量 2.01 ×1011N/m2，泊松比 0.3。

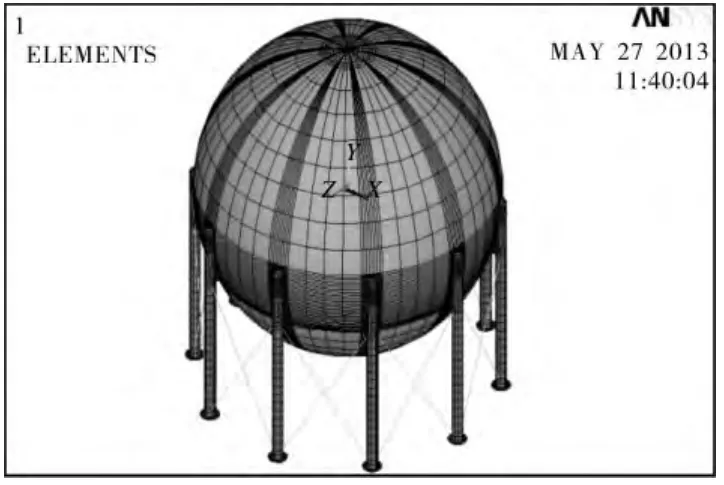
图1 球罐结构有限元模型

1.2 地震波的选取

地震运动输入是进行结构地震反应分析的依据，它对结构的地震反应影响很大。结构的地震反应以及破坏与否，除和结构的动力特性、弹塑性变形性质和变形能力有关外，还和地震波的特性(幅值、频谱特性和持续时间)密切相关。地震地面运动在时间和空间上都具有高度的变化性。在一般的结构地震反应分析中，往往只考虑它们的时间变化性，而不考虑它们的空间变化性［14］。

(1)幅值调整。

在抗震分析时，以地震过程中的加速度最大值作为强度指标。对选用的地震记录加速度峰值，应按照适当的比例放大或缩小，使其相当于和设防烈度相应的多遇地震及罕遇地震的加速度峰值。加速度峰值按下式调整:

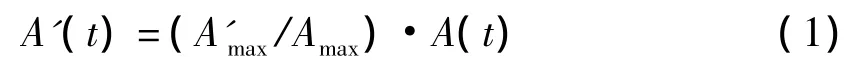
式中 A'(t)，A'max——地震波时程曲线与峰值，A'max取设防烈度要求的多遇或罕遇地震的地面运动峰值

A(t)，Amax——原地震波时程曲线与峰值

(2)频谱特性。

地震频谱特征包括谱形状、峰值和卓越周期等因素，与震源机制、地震波传播途径、反射、折射、散射和聚焦以及场地土特性、局部地质条件等多种因素相关。研究表明，在强震发生时，一般场地地面运动的卓越周期将与场地土的自振周期接近［15］。在选用地震波时，震中距应尽可能与拟建场地的震中距一致。

(3)地震持续时间。

地震持续时间有不同定义方法，如绝对持时、相对持时和等效持时。工程上常用的是相对持时，即根据地震波的振动幅或能量的相对量来定义。选择持续时间的原则是:

1)保证选择的持续时间内包含地震记录最强部分;

2)当对结构进行最大地震反应分析时，持续时间可选短些;当分析地震作用下结构的耗能过程时，应选择得长些;

3)尽量选择足够长的持续时间，一般建议取f≥10T(T为结构周期)。

文中选用适应于Ⅲ类软弱场地的1976年宁河天津波，对原始数据做了如下处理。根据国家地震局批准的烈度表，基本烈度为7，8，9度时，地面运动的最大水平加速度 Amax分别为0.125g，0.25g，0.5g。而实际地震记录，天津地震记录Amax=75.56 cm/s2。

因此，计算必须将实际地震记录的峰值折算成所需的基本烈度。一般A'max=Amax/2，文中选用7级地震，对于天津波水平的一个方向的记录应该乘以0.8687，如图2所示。对于地震波的输入，可以将加速度记录做成文件，利用APDL的读取功能读入到预先定义的数组中，在求解过程中按顺序施加到模型中。地震加速度记录的调整可以通过APDL的数学运算来完成。

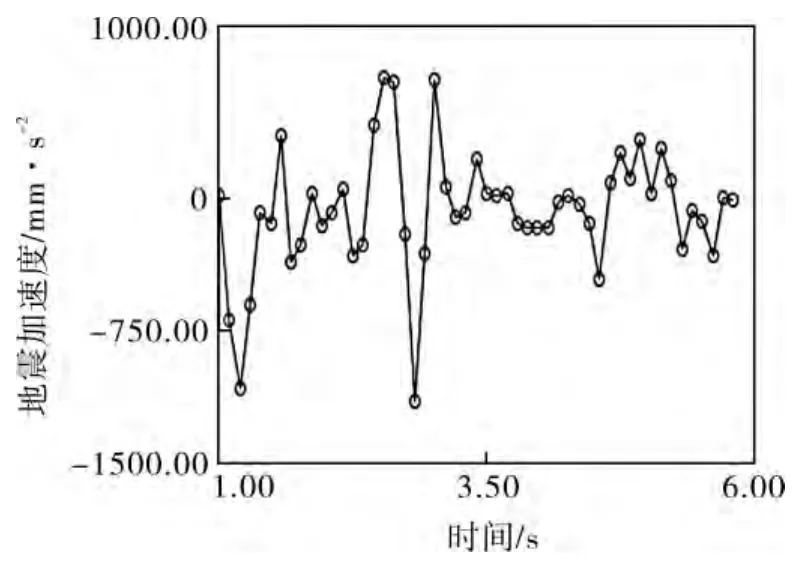
图2 调整后的地震波图

2 时程分析

时程分析法是将实际地震的加速度时程记录输入到结构计算模型中，直接分析结构地震反应的一种精确方法。通过采用逐步积分的方法获得地震过程中结构节点各时刻的位移、速度和加速度，从而计算每一瞬时构件的地震内力，结构从弹性到非弹性阶段构件破坏过程［16］。

假设球罐结构具有N个独立自由度，地震作用下球罐体系的动力方程可表示为:

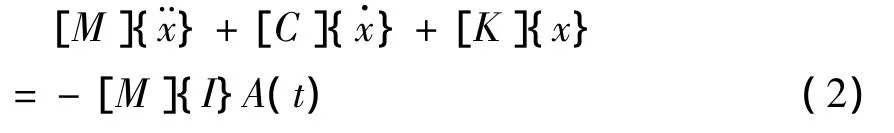
式中 ［M］，［C］，［K］——球罐系统的总质量矩阵、阻尼矩阵和总刚度矩阵——球罐震动位移、速度、加速度向量

A(t)——输入的地震波

通常采用直接积分法或振型叠加法求解方程(2)。振型叠加法，首先得到无阻尼自由振动振型;然后对方程(2)进行正交性变换;最后进行积分叠加［17］。

3 球罐抗震性能分析

3.1 典型球罐地震反应分析

通过模态分析，得到球罐结构前三阶频率，如表1所示。

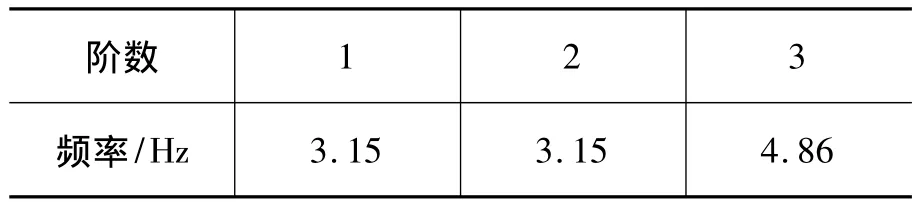
表1 球罐前三阶振动频率

将图2的地震波输入到有限元模型中，分析2000 m3球罐的地震反应，得到最大应力时刻应力云图如图3所示。可以看出，拉杆与支柱交界处应力最大，其次是托板与支柱交接处。根据球罐设计规范［4］，计算结果满足规范的强度要求。

3.2 球罐支撑结构参数对球罐抗震性能的影响

GB 12337—1998《钢制球型储罐》是我国球罐设计制造的现行标准，但其对非承压元件支柱(承重)和拉杆的设计还不够完善。球罐承受的水平荷载(风荷载和地震荷载)是由拉杆和支柱共同承受，因此，选择合适的支柱和拉杆对支撑结构以及整个球罐的抗震性能都有一定的影响［18］。当球罐承受地震荷载或风荷载时更为明显。以下分析2000 m3球罐支撑结构设计参数中支柱数目、直径及拉杆直径等的变化对球罐抗震性能的影响。

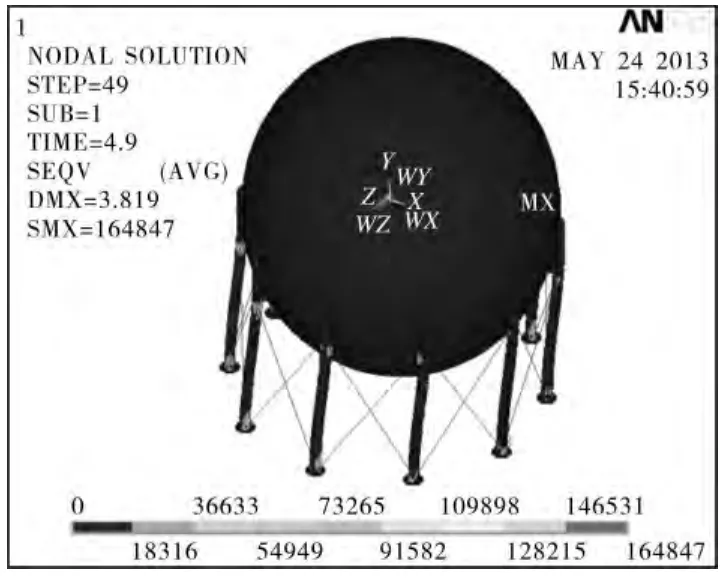
图3 最大应力云图(kPa)

为了验证单一参数对结构抗震性能的影响，在有限元计算中，每次仅改变某一参数值，其他结构参数保持原来模型的参数值。

由图4～6可以看出，随着拉杆直径、支柱直径的增大，支柱数目的增加，球罐的固有频率增大，可见支撑参数的改变对自振频率是有影响的。由于支撑参数不同，整个支撑结构的刚度就不同，另外在相同载荷作用下，支撑体系所受的拉应力大小不同，产生的拉伸变形程度也不同，因而自振频率不同。

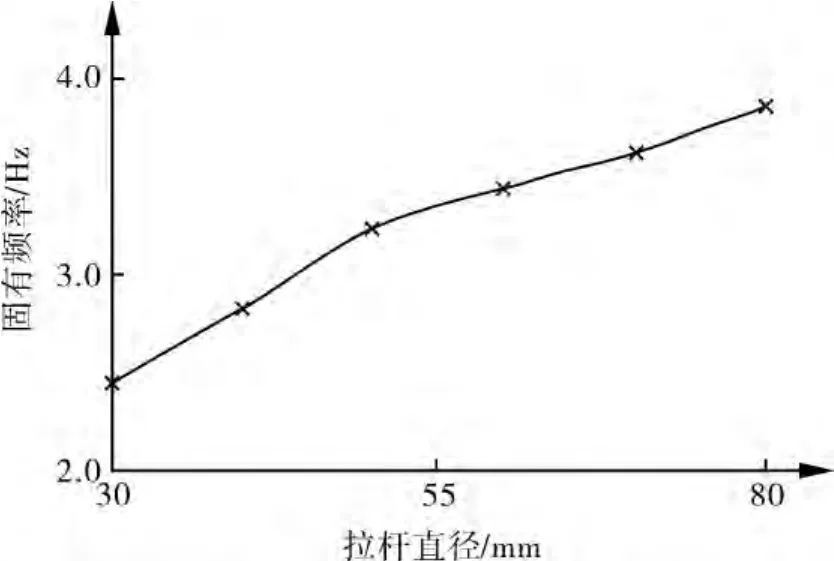
图4 拉杆直径变化对固有频率的影响

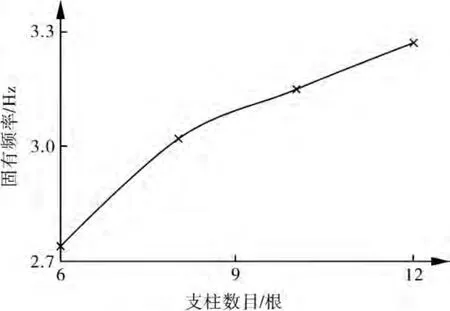
图5 支柱根数变化对固有频率的影响

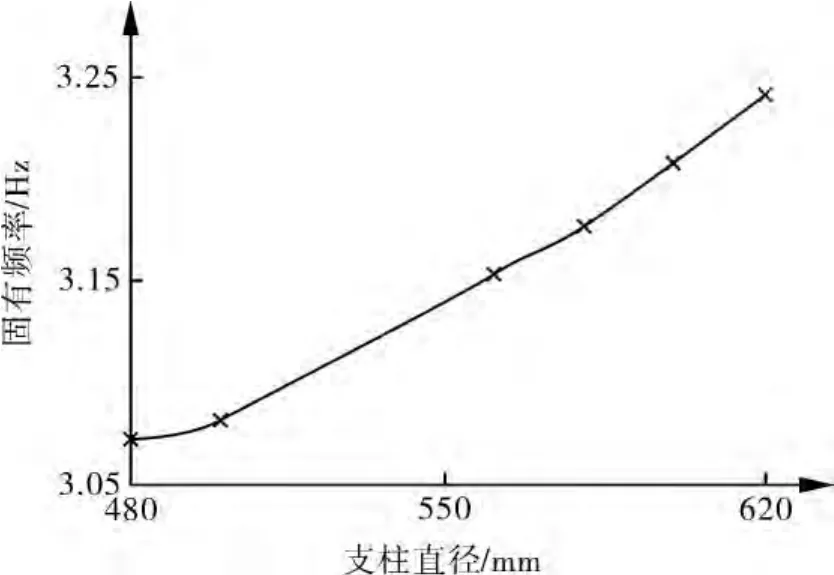
图6 支柱直径变化对固有频率的影响

图7～9可以看出，随着拉杆直径、支柱直径的增大，支柱数目的增加，球罐的最大应力整体趋势是减小的。

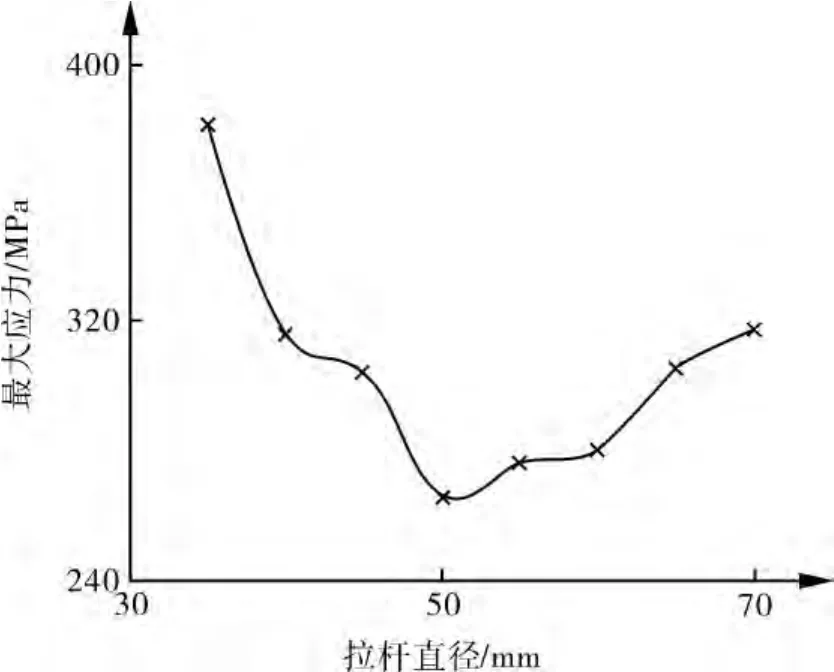
图7 拉杆直径变化对最大应力的影响

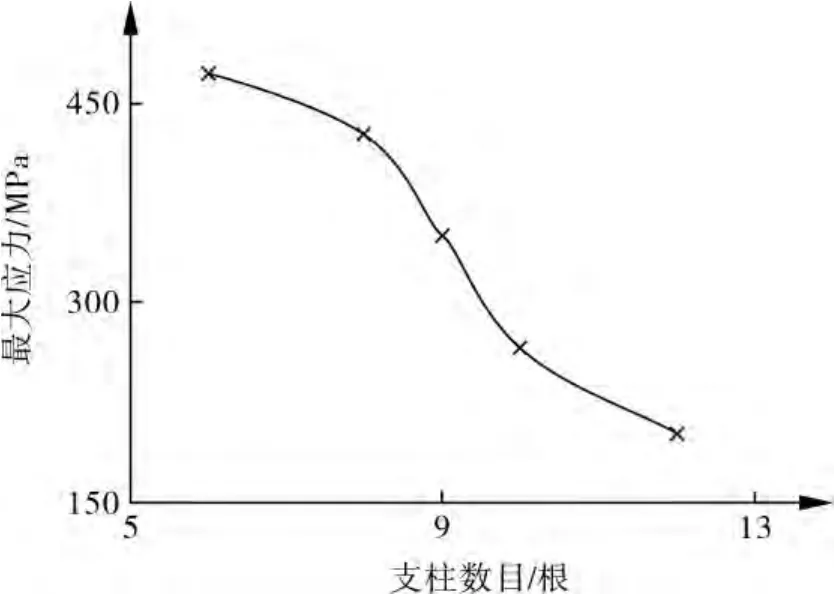
图8 支柱根数变化对最大应力的影响

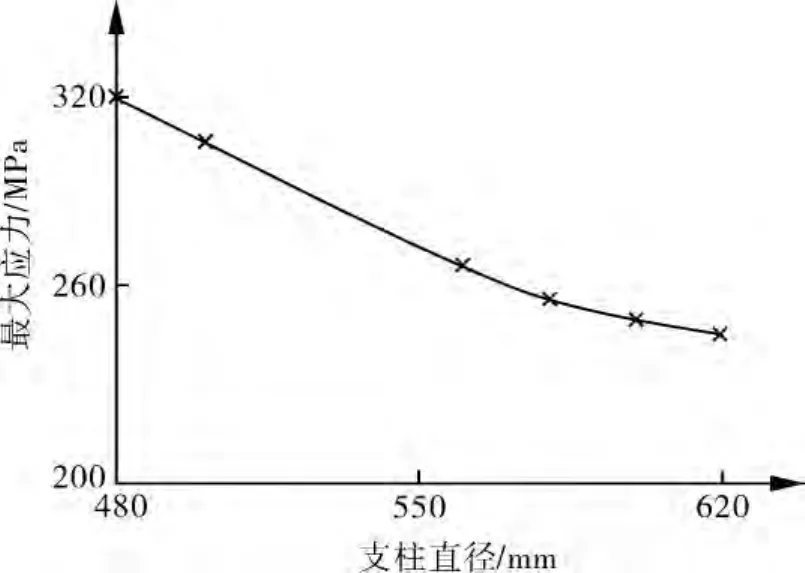
图9 支柱直径变化对最大应力的影响

拉杆直径由35 mm增大至70 mm的过程，球罐结构的最大应力出现先逐渐降低后增加的趋势;支柱直径从480 mm增大至620 mm和支柱根数由6根增加到12根的过程中，球罐结构的最大应力是逐渐降低的，并且趋势逐渐变缓。拉杆和支柱作为球罐的支撑结构，在一定限度上有效地增强了球壳的刚度，限制了球罐的整体变形，因此降低了球罐各个部位的结构应力。

同时，当拉杆和支柱直径太小或支柱数目太少时，支撑结构的整体刚度小，结构抵抗横向变形的能力弱。显著的弹性变形，将引起结构不连续部位的应力值过大。

但由图7的现象分析，笔者认为拉杆直径选择较大时，由于拉杆对球罐结构的水平刚度影响较大，导致了球罐的整体刚度变大，结构抵抗横向变形的能力增大的同时，刚度过大，结构的变形能力差，在强烈的地震荷载作用下，易造成球罐结构局部受损。所以，拉杆的直径越大，并不代表球罐的抗震性能越好。在设计中，应该分析其经济性和安全性的最优参数。

3.3 球罐容积变化对抗震性能的影响

针对支撑结构的参数对不同容积的球罐抗震性能的影响，文中按照球罐容积大小，选取5个典型的现役球罐，基本参数如表2所示。

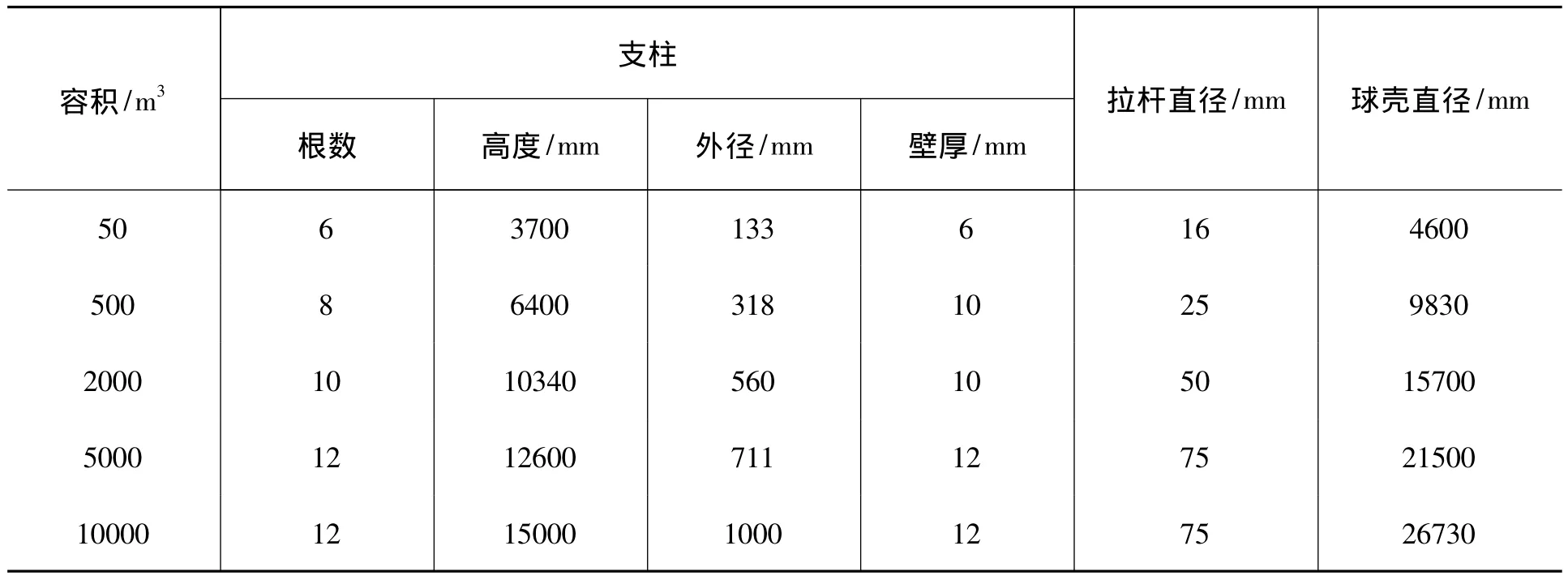
表2 球罐的基本参数

由图10，11可以看出，随着球罐容积的增加，结构的固有频率显著下降;结构在地震荷载激励下最大应力明显增大。由于球罐容积增大，地震发生时，支撑结构所受的水平力增加，同时球罐的重心距离较远，对支柱的弯矩也增大。通过以上计算可以看出，地震对大、中型球罐影响较大。可见大型球罐的基本设计不能照搬小型球罐，应该基于球罐的抗震性能及地震作用下主要控制失效模式，开展大型球罐的抗震基本设计，并采用合理的震动控制策略。

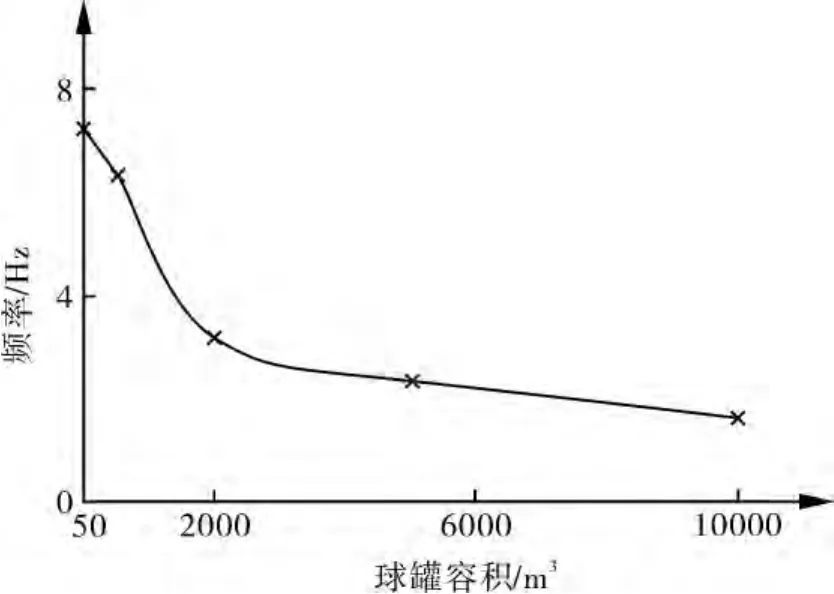
图10 球罐容积变化对固有频率的影响

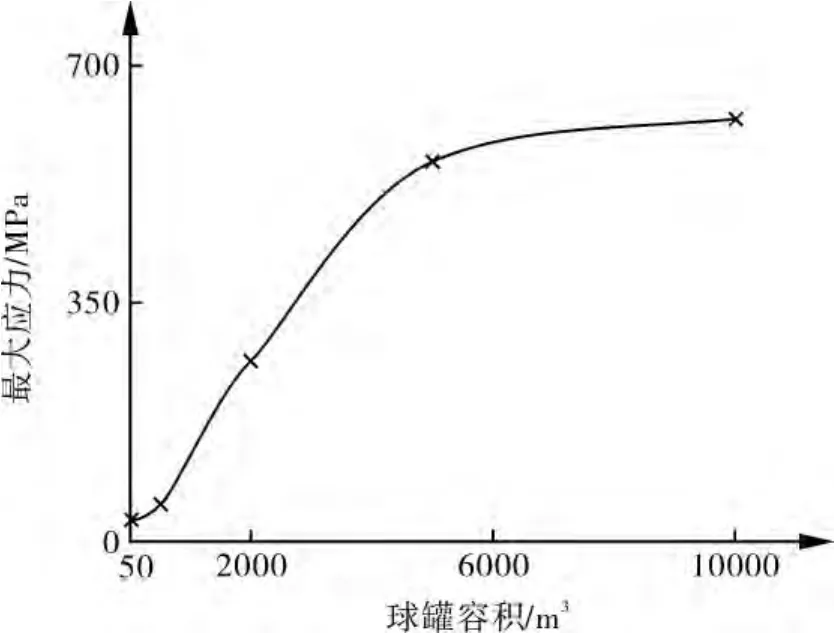
图11 球罐容积变化对最大应力的影响

4 结论

(1)通过典型球罐地震反应分析，可以看出拉杆与支柱连接处应力较为显著，设计中应考虑支耳连接，并采用加强处理。

(2)球罐支撑结构设计参数对系统的固有频率和最大应力有一定的影响，球罐容积的变化影响最大;其次是支柱数目;再次是拉杆直径;最后是支柱直径。

(3)在满足拉杆和支柱强度要求的前提下，选择较小的拉杆和支柱规格尺寸，一方面可以减少材料用量;另一方面可减小球罐地震载荷效应，从而提高结构抗震性能。

(4)小型球罐的抗震性能较好，而大、中型球罐的地震荷载效应较为显著。

(5)文中的研究可为球罐抗震安全保障及设计提供合理依据。

［1］徐英，杨一凡，朱萍，等.球罐和大型储罐［M］.北京:化学工业出版社，2005.

［2］李永泰，顾永干，郭春光，等.1000 m3液氨球罐地震失效分析［J］.压力容器，2014，31(1):56－61.

［3］郭春光，李永泰，黄金国，等.球罐整体结构自振周期计算及地震响应分析［J］.压力容器，2012，29(7):28－32.

［4］GB 12337—1998，钢制球形储罐［S］.

［5］梅林涛，杨国义，寿比南.球形储罐应力分析及评定［J］.压力容器，2002，19(7):15－17.

［6］项忠权，孙家孔.石油化工设备抗震［M］.北京:地震出版社，1995:232－269.

［7］SHIBATA H.Seismic hazard and damage—avoiding disaster through simulation，experiment and experience［J］.Journal of Pressure Vessel Technology，1999，121(1):30－36.

［8］汪辉.液氨球罐的震后修复［J］.化工机械，2009，36(2):165－167.

［9］蒋宏业，姚安林，郑兴华，等.天然气球罐失效故障树分析［J］.天然气工业，2003，23(6):143－145.

［10］程凌，王宗宁，陶陈华.球罐结构应力与抗震分析研究［J］.石油化工设备，2010，39(1):17－21.

［11］ORTIZ J L，BARHORST A.Closed－form modeling of fluid-structure interaction with nonlinear sloshing:Potential flow［J］.AIAA Journal，1997，35(9):1510－1517.

［12］肖志刚.球形储液罐地震反应分析及减震方法研究［D］.哈尔滨:哈尔滨工程大学，2006.

［13］戴鸿哲，王伟，肖志刚.球形储液罐液－固耦联地震反应及减震方法［J］.哈尔滨工业大学学报，2010，42(4):515－520.

［14］白峻昶，靳金平.时程分析用地震波选取的探讨［J］.山西建筑，2007，33(3):62－63.

［15］陶夏新，刘曾武.工程场地条件评定中的地脉动研究［J］.地震工程与工程振动，2001，21(4):18－23.

［16］杨志勇，黄吉锋，邵弘.弹性与弹塑性动力时程分析方法中若干问题探讨［J］.建筑结构学报，2009，(增刊1):213－217.

［17］张大勇，岳前进，李刚，等.冰振下海洋平台上部天然气管线振动分析［J］.天然气工业，2006，26(12):139－141.

［18］李准，尹侠.地震载荷下拉杆直径对球罐的影响分析［J］.化工机械，2007，34(5):260－263.